Contents
- 1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
- 2 Hard Decision vs. Soft Decision
- 3 Reliability information - Log Likelihood Ratio
- 4 Symbol-wise soft in soft out decoding
- 5 Calculation of extrinsic LLRs
- 6 BCJR decoding: Forward-backward algorithm
- 7 Basic structure of concatenated coding systems
- 8 Exercises for the chapter
- 9 Quellenverzeichnis
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
The last main chapter of the channel coding book describes iterative decoding techniques as used in most of today's (2017) communication systems. This is due to the following reasons:
- To approach the channel capacity, one needs very long codes.
- But for long codes, blockwise maximum likelihood decoding is almost impossible.
The decoder complexity can be significantly reduced with almost the same quality if two (or more) short channel codes are linked together and the newly acquired (soft) information is exchanged between the decoders at the receiver in several steps - i.e. iteratively.
The breakthrough in the field came in the early 1990s with the invention of turbo codes by "Claude Berrou" and shortly thereafter with the rediscovery of low-density parity-check codes by "David J. C. MacKay" and "Radford M. Neal", after the LDPC codes developed as early as 1961 by "Robert G. Gallager" had been forgotten in the meantime.
Specifically, the fourth main chapter discusses:
- a comparison of Hard Decision and Soft Decision,
- the quantification of reliability information' by log likelihood ratios (LLR),
- the principle of symbol-wise soft in soft out (SISO) decoding,
- the definition of apriori L value, a posteriori L-value and extrinsic L value,
- the basic structure of serially concatenated and parallel concatenated coding systems, respectively,
- the characteristics of product codes and their hard decision decoding,
- the basic structure, decoding algorithm and performance of turbo codes,
- basic information on the low-density parity-check codes and their applications.
Hard Decision vs. Soft Decision
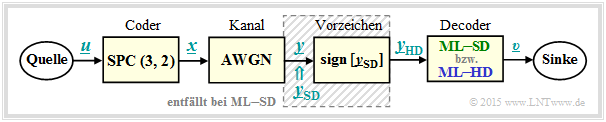
To introduce the topic discussed here, let us consider the following message transmission system with coding.
In the following, all symbols are given in bipolar representation: "$0$" → "$+1$" and "$1$" → "$-1$".
- The symbol sequence $\underline{u} = (u_1, \ u_2)$ is assigned to the code sequence $\underline{x} = (x_1, \ x_2, \ x_3) = (u_1, \ u_2, \ p)$ where for the parity bit $p = u_1 ⊕ u_2$ holds ⇒ "Single Parity–check Code" ⇒ ${\rm SPC} (3, 2, 2)$.
- The "AWGN–channel" changes the binary symbols $x_i ∈ \{+1, \ –1\}$ to real-valued output values $y_i$, for example according to $\text{channel 4}$ the table below: $x_1 = +1$ ⇒ $y_1 = +0. 9$, $x_2 = \, -1$ ⇒ $y_2 = +0.1$ and $x_3 = \, -1$ ⇒ $y_3 = +0.1$.
- Decoding is done according to the criterion "Maximum-Likelihood" $\text{(blockwise ML)}$, distinguishing between hard decision $\rm {(ML–HD)}$ and soft decision $\rm {(ML–SD)}$ .
- The whole block diagram corresponds to $\rm ML–HD$. Here, only the signs of the AWGN output values ⇒ $y_{\rm HD, \ \it i} = {\rm sign}\big [y_{\rm SD, \ \it i}\big ]$ are evaluated for decoding. In soft decision $\rm {(ML–SD)}$ one omits the shaded block and directly evaluates the continuous value input variables $y_{\rm SD, \ \it i}$ .
For all columns of this table it is assumed:
- the message block $\underline{u} = (0, 1)$, bipolar representable as $(+1, \, –1)$,
- the ${\rm SPC} \ (3, 2)$–coded block $\underline{x} = (0, 1, 1)$ respectively in bipolar representation $(+1, \, -1, \, -1)$.
Thus, the four columns differ only by different AWGN realizations.
$\text{Definition:}$ From the example table you can see:
- $\text{Hard Decision:}$ The symbol sequence $\underline{v}_{\rm HD}$ results from the hard decided channel values $\underline{y}_{\rm HD}$ (blue background).
In our example, only the constellations according to $\text{channel 1}$ and $\text{channel 2}$ are decoded without errors.
- $\text{Soft Decision:}$ The symbol sequence $\underline{v}_{\rm SD}$ results from the "soft" channel output values $\underline{y}_{\rm SD}$ (green background).
Now, in this example, it is also correctly decided at $\text{channel 3}$
The entries in the example table above are to be interpreted as follows:
- For ideal channel ⇒ $\text{channel 1}$ ⇒ $\underline{x} = \underline{y}_{\rm SD} = \underline{y}_{\rm HD}$ there is no difference between the (blue) conventional hard decision variant $\rm {(ML–HD)}$ and the (green) soft decision variant $\rm {(ML–SD)}$.
- Setting according $\text{channel 2}$ demonstrates low signal distortions. Because of $\underline{y}_{\rm HD} = \underline{x}$ (which means that the channel does not distort the signs) also $\rm ML–HD$ gives the correct result $\underline{v}_{\rm HD} = \underline{u}$.
- For $\text{channel 3}$ there is $\underline{y}_{\rm HD} ≠ \underline{x}$ and there is also no ${\rm SPC} \ (3, 2)$–assignment $\underline{u}$ ⇒ $\underline{y}_{\rm HD}$. The ML–decoder reports here by outputting $\underline{v}_{\rm HD} = \rm (E, \ E)$ that it failed in decoding this block. "$\rm E$" stands for "Erasure" .
- Also the soft decision decoder recognizes that decoding based on the signs does not work. Based on the $\underline{y}_{\rm SD}$–values, however, it recognizes that with high probability the second bit has been corrupted and decides to use the correct symbol sequence $\underline{v}_{\rm SD} = (+1, \, -1) = \underline{u}$.
- In $\text{channel 4}$ both the signs of bit 2 and bit 3 are changed by the AWGN–channel, leading to the result $\underline{v}_{\rm HD} = (+1, +1) ≠ \underline{u}(+1, \, -1)$ ⇒ a block error and a bit error at the same time. Also the soft decision decoder gives the same wrong result here.
The decoding variant "ML–SD" also offers the advantage over "ML–HD" that it is relatively easy to assign a reliability value to each decoding result (in the above table, however, this is not specified). This reliability value
- would have its maximum value at $\text{channel 1}$ ,
- would be significantly smaller for $\text{channel 2}$ ,
- would be close to zero for $\text{channel 3}$ and $\text{channel 4}$ .
Reliability information - Log Likelihood Ratio
Let $x ∈ \{+1, \, -1\}$ be a binary random variable with probabilities ${\rm Pr}(x = +1)$ and ${\rm Pr}(x = \, -1)$. For coding theory, it proves convenient in terms of computation times to use the natural logarithm of the quotient instead of the probabilities ${\rm Pr}(x = ±1)$ .
$\text{Definition:}$ The log likelihood ratio (LLR) of the random variable $x ∈ \{+1, \, -1\}$ is:
- \[L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.\]
For unipolar/symbolic representation $(+1 → 0$ and $-1 → 1)$ applies accordingly with $\xi ∈ \{0, \, 1\}$:
- \[L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.\]
Below is given the nonlinear relationship between ${\rm Pr}(x = ±1)$ and $L(x)$ . Replacing ${\rm Pr}(x = +1)$ with ${\rm Pr}(\xi = 0)$, the middle row gives the $L$–value of the unipolar random variable $\xi$.
You can see:
- The more likely random value of $x ∈ \{+1, \, -1\}$ is given by the sign ⇒ ${\rm sign} \ L(x)$ given.
- In contrast, the absolute value ⇒ $|L(x)|$ indicates the reliability for the result ${\rm sign}(L(x))$ .
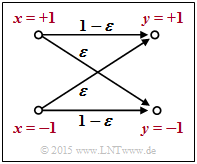
$\text{Example 1:}$ We consider the outlined "BSC model" with bipolar representation. Here, with the corruption probability $\varepsilon = 0.1$ and the two random variables $x ∈ \{+1, \, -1\}$ and $y ∈ \{+1, \, -1\}$ at the input and output of the channel:
- \[L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = +1) }{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = -1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} \big[(1 - \varepsilon)/\varepsilon \big]\\ {\rm ln} \hspace{0.15cm}\big [\varepsilon/(1 - \varepsilon)\big] \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = +1, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}\]
For example, $\varepsilon = 0.1$ results in the following numerical values (compare upper table):
- \[L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.8cm} L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.\]
This example shows that the so-called LLR algebra can also be applied to conditional probabilities.
In the "Exercise 4.1Z" the BEC–model is described in a similar way.
$\text{Example 2:}$ In another example, now consider the "AWGN channel" with the conditional probability density functions
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
In the graphic, two exemplary Gaussian functions are shown as blue and red curves, respectively.
The total PDF of the output signal $y$ is obtained from the (equally) weighted sum:
- \[f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert \hspace{0.05cm}x=-1 ) \big ] \hspace{0.05cm}.\]
We now calculate the probability that the received value $y$ lies in a (very) narrow interval of width $\Delta$ around $y_0 = 0.25$ . One obtains approximately
- \[{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[{\rm Pr} (\vert y - y_0\vert \le {\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
The slightly larger vertical lines denote the conditions, the smaller ones the absolute value.
The LLR of the conditional probability in the forward direction $($meaning: output $y$ for a given input $x)$ is thus obtained as the logarithm of the quotient of both expressions:
- \[L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. \]
If we now replace the auxiliary $y_0$ with the (general) random $y$ at the AWGN output, the final result is:
- \[L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. \]
Here $K_{\rm L} = 2/\sigma^2$ is a constant that depends solely on the standard deviation of the Gaussian
.
Symbol-wise soft in soft out decoding
We now assume a $(n, \ k)$–block code where the codeword $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ is corrupted by the channel into the received word $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$ .
- For long codes, a maximum a posteriori block-level decision – is short: $\text{ "block wise MAP"}$ – very elaborate.
- One would have to find among the $2^k $ allowable codewords $\underline{x}_j ∈ \mathcal{C}$ the one with the greatest probability of inference ( A Posteriori Probability, APP).
- The codeword to output $\underline{z}$ in this case would be $\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$
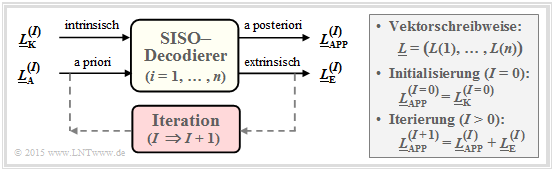
A second possibility is decoding on bit level. The represented symbol-wise (or bit-wise) $\text{soft in soft out decoder}$ has the exercise to decode all codeword bits $x_i ∈ \{0, \, 1\}$ according to maximum inference probability (APP) ${\rm Pr}(x_i | \underline{y})$ . With the running variable $i = 1, \text{...} , \ n$ holds in this case:
- The corresponding LLR for the $i$th code bit is:
- \[L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . \]
- The decoder works iteratively. At initialization $($indicated in the diagram by the parameter $I = 0)$ is $L_{\rm APP}(i) = L_{\rm K}(i)$, where the channel LLR $L_{\rm K}(i)$ is given by the received value $y_i$ .
- In addition, the extrinsic LLR $L_{\rm E}(i)$ is calculated, which quantifies the total information provided by all other bits $(j ≠ i)$ due to the code–properties about the considered $i$th bit.
- At the next iteration $($ab $I = 1)$ $L_{\rm E}(i)$ is taken into account in the computation of $L_{\rm APP}(i)$ as apriori information $L_{\rm A}(i)$ . Thus, for the new a posteriori LLR in iteration $I + 1$ holds:
- \[L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . \]
- The iterations continue until all absolute values $|L_{\rm APP}(i)|$ are greater than a given value. The most likely codeword $\underline{z}$ is then obtained from the signs of all $L_{\rm APP}(i)$, with $i = 1, \ \text{...} , \ n$.
- For a "systematic code" the first $k$ bits of $\underline{z}$ indicate the information word being searched for, which will most likely match the message $\underline{u}$ being sent.
This description of the SISO decoder after [Bos98][1] is intended at this point primarily to clarify the different $L$–values. One recognizes the large potential of the symbol-wise decoding only in connection with "concatenated coding systems".
Calculation of extrinsic LLRs
The difficulty in symbol-wise iterative decoding is generally the provision of the extrinsic LLRs $L_{\rm E}(i)$. For a code of length $n$ here, for the run variable: $i = 1, \ \text{...} , \ n$.
$\text{Definition:}$ The extrinsic LLR is a measure of the information that the other symbols $(j ≠ i)$ of the codeword provide about the $i$–th code symbol, expressed as a log likelihood ratio. We denote this characteristic value by $L_{\rm E}(i)$.
We now calculate the extrinsic LLRs $L_{\rm E}(i)$ for two example codes.
$\text{Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$
A repetition code is characterized by the fact that all $n$ code symbols $x_i ∈ \{0, \, 1\}$ are identical. The extrinsic LLR for the $i$&th symbol is very easy to specify here and is:
- \[L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
- If the sum over all $L_{j ≠ i}$ is positive, this implies a preference for the decision $x_i = 0$ from the point of view of the other LLR.
- On the other hand, if the sum is negative $x_i = 1$ is more likely.
- $L_{\rm E}(i) = 0$ does not allow prediction.
$\text{Example 5:}$ We consider the decoding of the repetition code $\text{RC (4, 1,4)}$. We make three different assumptions for the Log Likelihood Ratio $\underline{L}_{\rm A}^{(I=0)} = \underline{L}_{\rm APP}$ .
$\text{Decoding example (A):}$
- $$\underline{L}_{\rm APP} = (+1, -1, +3, -1)\text{:}$$
- $$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$
- $$L_{\rm E}(2) = +1+3-1 = +3\hspace{0.05cm},$$
- $$L_{\rm E}(3) = +1-1 -1= -1\hspace{0.05cm},$$
- $$L_{\rm E}(4) = +1-1 +3 = +3\hspace{0.05cm}$$
- $$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm A}^{(I=1)}=\underline{L}_{\rm A}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$
- At the beginning $(I=0)$ the positive $L_{\rm E}$–values indicate $x_1 = 0$, $x_2 = 0$ and $x_4 = 0$ while $x_3 =1$ is more likely.
- Already after one iteration $(I=1)$ all $L_{\rm A}$–values are positive ⇒ information bit is decoded as $u = 0$ .
- Further iterations yield nothing.
$\text{Decoding example (B):}$ $$\underline{L}_{\rm APP} = (+1, +1, -4, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$
- Although three signs were wrong at the beginning, after two iterations all $L_{\rm A}$–values (LLR) are negative.
- The information bit is decoded as $u = 1$ .
$\text{Decoding example (C):}$ $$\underline{L}_{\rm APP} = (+1, +1, -3, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$
- All $L_{\rm A}$–values (LLR) are zero already after one iteration.
- The information bit cannot be decoded, although the initial situation was not much worse than with $\rm (B)$.
- Further iterations bring nothing here either.
$\text{Single Parity–check code}$ ⇒ ${\rm SPC} \ (n, \ n \, -1, \ 2)$
For each Single Parity–check Code the number of ones in each codeword is even. Or, put another way, For each codeword $\underline{x}$ the "Hamming weight" $w_{\rm H}(\underline{x})$ is even.
$\text{Definition:}$ Let the codeword $\underline{x}^{(–i)}$ contain all symbols except $x_i$ ⇒ vector of length $n -1$. Thus, the $\text{extrinsic }LLR$ is with respect to the $i$–th symbol when $\underline{x}$ was received:
- \[L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.\]
As will be shown in the "Task 4.4" , it is also possible to write for this:
- \[L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
$\text{Example 6:}$ We assume Single Parity–check code with $n = 3, \ k = 2$ ⇒ briefly ${\rm SPC} \ (3, \ 2, \ 2)$ from.
The $2^k = 4$ valid codewords $\underline{x} = \{x_1, x_2, x_3\}$ are for bipolar description ⇒ $x_i ∈ \{±1\}$:
- $$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$
- $$\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$
So, with this code, the product $x_1 \cdot x_2 \cdot x_3$ is always positive.
The above table shows the decoding process for $\underline{L}_{\rm APP} = (+2.0, +0.4, \, –1.6)$. The hard decision according to the signs of $L_{\rm APP}(i)$ would yield here $(+1, +1, \, -1)$, thus no valid codeword of ${\rm SP}(3, \ 2, \ 2)$.
On the right side of the table, the corresponding extrinsic LLRs are entered:
- \[L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, \]
- \[L_{\rm E}(2) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, \]
- \[L_{\rm E}(3) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.\]
The second equation can be interpreted as follows:
- $L_{\rm APP}(1) = +2.0$ and $L_{\rm APP}(3) = \, -1.6$ state that the first bit is more likely to be $+1$ than $-1$ and the third bit is more likely to be $-1$ than $+1$. The reliability (the amount) is slightly greater for the first bit than for the third.
- The extrinsic information $L_{\rm E}(2) = \, -0.518$ considers only the information of bit 1 and bit 3 about bit 2. From their point of view, the second bit is a $-1$ with reliability $0.518$.
- The $y_2$ value derived from the received LLR ⇒ $L_{\rm APP}(2) = +0.4$ has suggested a $+1$ for the second bit. The discrepancy is resolved here already in the iteration $I = 1$ .
- Decided here for the codeword $\underline{x}_1$. For $0.518 < L_{\rm APP}(2) < 1.6$ the result $\underline{x}_1$ would only be available after several iterations. For $L_{\rm APP}(2) > 1.6$ on the other hand, the decoder returns $\underline{x}_0$.
BCJR decoding: Forward-backward algorithm
An example of iterative decoding of convolutional codes is the BCJR algorithm, named after its inventors L. R. Bahl, J. Cocke, F. Jelinek, and J. Raviv ⇒ [BCJR74][2]. The algorithm has many parallels to the seven-year older Viterbi–decoding, but also some significant differences:
- While Viterbi estimates the total sequence ⇒ $\text{"block–wise maximum likelihood"}$, the BCJR– Algorithm minimizes the bit error probability ⇒ $\text{"bit–wise MAP"}$.
- The Viterbi algorithm (in its original form) cannot process soft information. In contrast, the BCJR algorithm specifies a reliability value for each individual symbol (bit) at each iteration, which is taken into account in subsequent iterations.
The figure is intended – to illustrate in an almost inadmissibly simplified – way the different approach of the Viterbi–algorithm (left) and the BCJR–algorithm (right). This is based on a convolutional code with memory $m = 1$ and length $L = 4$ ⇒ total length (with termination) $L' = 5$.
- The Viterbi–algorithm searches and finds the most likely path from ${\it \Gamma}_0(S_0)$ to ${\it \Gamma}_5(S_0)$, namely $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. We refer to the sample solution to "Exercise 3.9Z".
The sketch for the BCJR–algorithm illustrates the extraction of the extrinsic $L$–value for the third symbol ⇒ $L_{\rm E}(3)$. The relevant area in the trellis is shaded:
- Working through the trellis diagram in the forward direction, one – in the same way as Viterbi – obtains the metrics $\alpha_1, \ \alpha_2, \ \text{...}\hspace{0.05cm} , \ \alpha_5$. To calculate $L_{\rm E}(3)$ one needs from this $\alpha_2$.
- Then we traverse the trellis diagram backwards (i.e. from right to left) and thus obtain the metrics $\beta_4, \ \beta_3, \ \text{...}\hspace{0.05cm} , \ \beta_0$ corresponding to the sketch below.
- The extrinsic LLR $L_{\rm E}(3)$ sought is obtained from the metrics $\alpha_2$ (in the forward direction) and $\beta_3$ (in the backward direction) and the apriori–information $\gamma_3$ about the symbol $i = 3$.
Basic structure of concatenated coding systems
The most important communication systems of the last years use two different channel codes. One speaks then of concatenated codes. Even with relatively short component codes $\mathcal{C}_1$ and $\mathcal{C}_2$ the concatenated code $\mathcal{C}$ results in a sufficiently large codeword length $n$, which is known to be necessary to approach the channel capacity.
To begin with, here are a few examples from mobile communications:
- In "GSM" (Global System for Mobile Communications, second generation of mobile communications), the data bit rate is first increased from $9. 6 \ \rm kbit/s$ to $12 \ \rm kbit/s$ in order to enable error detection in circuit-switched networks as well. This is followed by a punctured convolutional code with the output bit rate $22.8 \rm kbit/s$. The total code rate is thus about $42.1\%$.
- In the 3G–cellular system "UMTS" (Universal Mobile Telecommunications System), depending on the boundary conditions (good/bad channel, few/many subscribers in the cell) one uses a "convolutional code" or a "turbo code" (by this one understands per se the concatenation of two convolutional encoders). In the 4G–mobile communications system "LTE" (Long Term Evolution), a convolutional code is used for short control signals and a turbo code for the longer payload data.
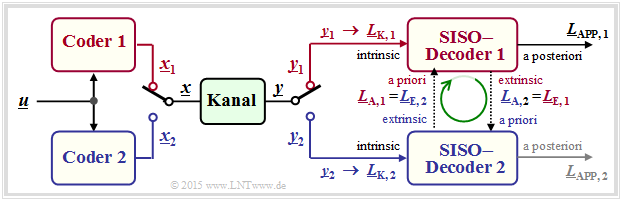
The graphic shows the basic structure of a parallel concatenated coding system. All vectors consist of $n$ elements: $\underline{L} = (L(1), \ \text{...}\hspace{0.05cm} , \ L(n))$. So the calculation of all $L$–values is done on symbol level. Not shown here is the "Interleaver", which is mandatory for turbo codes, for example.
- The code sequences $\underline{x}_1$ and $\underline{x}_2$ are combined to form the vector $\underline{x}$ for joint transmission over the channel by a multiplexer. At the receiver, the sequence $\underline{y}$ is again decomposed into the individual parts $\underline{y}_1$ and $\underline{y}_2$ . From this the channel–$L$–values $\underline{L}_{\rm K,\hspace{0.05cm}1} $ and $\underline{L}_{\rm K,\hspace{0.05cm}2}$ are formed.
- The symbol-wise decoder determines according to the "procedure" extrinsic LLR $\underline{L}_{\rm E,\hspace{0. 05cm} 1}$ and $\underline{L}_{\rm E,\hspace{0.05cm} 2}$, which are simultaneously the apriori information $\underline{L}_{\rm A,\hspace{0. 05cm} 2}$ and $\underline{L}_{\rm A,\hspace{0.05cm} 1}$ for the other decoder.
- After a sufficient number of iterations (i.e. when a termination criterion is met), the vector of a posteriori values ⇒ $\underline{L}_{\rm APP}$ is available at the decoder output. In the example, the value in the upper branch is taken arbitrarily. However, the lower LLR would also be possible.
The above model also applies in particular to the decoding of turbo–codes according to the chapter "Basic structure of turbo codes".
Exercises for the chapter
Aufgabe 4.1: Zum „Log Likelihood Ratio”
Aufgabe 4.1Z: L–Werte des BEC–Modells
Aufgabe 4.2: Kanal–LLR bei AWGN
Aufgabe 4.3: Iterative Decodierung beim BSC
Aufgabe 4.3Z: Umrechnungen von L–Wert und S–Wert
Aufgabe 4.4: Extrinsische L–Werte beim SPC
Aufgabe 4.4Z: Ergänzung zur Aufgabe 4.4
Aufgabe 4.5: Nochmals zu den extrinsischen L–Werten
Aufgabe 4.5Z: Tangens Hyperbolikus und Inverse
Quellenverzeichnis