Exercise 4.08Z: Basics about Interleaving

• Return to book

Interleaver description

Interleaving is required, for example, for a channel with burst error characteristics in order to distribute the errors within the burst over a sufficiently large area so that they can subsequently be largely corrected (or at least detected).

For turbo codes based on so-called  RSC encoder  (Recursive Systematic Convolutional Encoder)  – and only such make sense – interleaving is essential also with the AWGN channel, because then there are also always (some) input sequences, which deliver only zeros in the output sequence after quite a few ones, and that to infinity   ⇒   there are output sequences with very small Hamming weight.

If the bits of such input sequences are distributed over a wide range in the second coder, the problem can be (largely) eliminated by the interaction of both component decoders in the case of iterative symbol-wise decoding.

A general distinction is made between

• Block interleaver and
• Random interleaver.

In block interleaving  one fills a matrix with  $S$  columns and  $Z$  rows column by column and reads the matrix row by row. This deterministically scrambles a block of information with  $I_{\rm max} = S \cdot Z$  bits.

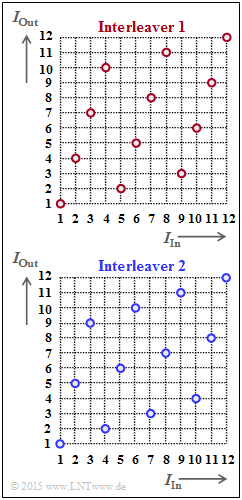
On the right, two interleavers are indicated and in graphical form by the assignment  $I_{\rm Out}(I_{\rm In})$. These quantities represent the "index of the output sequence" and the "index of the input sequence", respectively. It holds:

$$1 \le I_{\rm Out} \le I_{\rm max} \hspace{0.05cm}, \hspace{0.5cm} 1 \le I_{\rm In} \le I_{\rm max} \hspace{0.05cm}. $$

In the subtask  (1)  it is asked whether this is  block interleaving  or  random interleaving  . The latter are discussed in the  "theory section"  but only very briefly.

Hints:

• Die Aufgabe bezieht sich auf das Kapitel  "The Basics of Turbo Codes".

• Aber auch in anderen $\rm LNTwww$–Büchern wird Interleaving behandelt, unter anderem im Buch "Beispiele von Nachrichtensystemen" mit Bezug zum

• Standard  Digital Subscriber Line (DSL)   ⇒   "Interleaving und De–Interleaving",
• 2G–Mobilfunksystem  GSM   ⇒   "Komponenten der Sprach– und Datenübertragung",
• 3G–Mobilfunksystem  UMTS   ⇒   "Kanalcodierung",
• 4G–Mobilfunksystem  LTE   ⇒   "Funktionsweise von SC–FDMA"  (im Buch "Mobile Kommunikation").

Fragebogen

1

Welche Interleaver–Art ist in der Grafik auf der Angabenseite dargestellt?

	Block–Interleaving,
	Random–Interleaving.

2

Wieviele Zeilen  ($Z$)  und Spalten  ($S$)  hat die obere "Interleaver–Matrix 1"?

$Z \ = \ $

$S \ = \ $

3

Es gelte  $\underline{u} = (1001'0001'1101'1101'0010'0111)$. Wie beginnt die verwürfelte Folge  $\underline{u}_{\pi}$?
    Hinweis:   Die Hochkommata dienen nur als Lesehilfe.

	$\underline{u}_{\pi} = (110'100'100'011'111'110'010'001' \text{...}\ )$,
	$\underline{u}_{\pi} = (101'001'000'111'100'101'011'101'\text{...}\ )$.

4

Die verwürfelte Folge sei  $\underline{u}_{\pi} = (100'100'011'101'110'100'100'111)$. Wie lautet die Folge nach dem De–Interleaving?

	$\underline{u} = (1101'0010'0011'1111'1001'0001'\text{...}\ )$,
	$\underline{u} = (1010'0100'0111'1001'0101'1101' \text{...}\ )$.

Musterlösung

Solution

4×3–Interleaver–Matrix

(1)  Aus der regelmäßigen Struktur der Funktion $I_{\rm Out}(I_{\rm In})$ erkennt man, dass es sich um einen Blockinterleaver handelt  ⇒  Antwort 1.

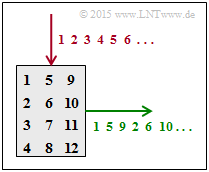
(2)  Der Index "1" wird als erstes Zeichen ausgegeben. Weiter gilt:

• Der Index 5 wird als zweites Zeichen ausgegeben  ⇒  $\underline{Z = 4}$.
• Der Index 2 wird als viertes Zeichen ausgegeben  ⇒  $\underline{S = 3}$.

Die obere Grafik zeigt für die 4×3–Interleaver–Matrix:

• das spaltenweise Beschreiben (rot),
• das zeilenweise Auslesen (grün).

Zum Interleaving

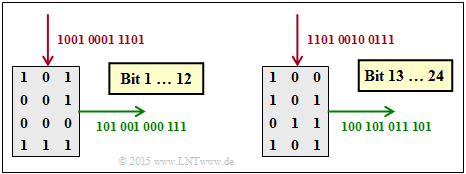
(3)  Richtig ist der der Lösungsvorschlag 2:

• Die Matrix wird spaltenweise beschrieben und zeilenweise ausgelesen.
• Nach 12 Bit wird die Matrix gelöscht und die Prozedur beginnt von Neuem.
• Die Grafik zeigt, dass nun der Lösungsvorschlag 2 richtig ist.

Zum De–Interleaving

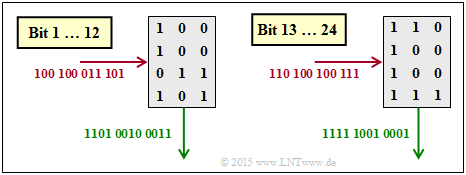
(4)  Richtig ist der der Lösungsvorschlag 1:

• Beim De–Interleaving wird die Matrix zeilenweise beschrieben und spaltenweise ausgelesen.
• Die Grafik zeigt, dass hier der Lösungsvorschlag 1 richtig ist.