xDSL as Transmission Technology

1 Possible bandwidth allocations for xDSL
2 ADSL bandwidth allocation in Germany
3 VDSL(2) bandwidth allocation
4 Overview of transmission methods
5 Basics of Quadrature Amplitude Modulation
6 Possible QAM signal space constellations
7 Carrierless Amplitude Phase Modulation (CAP)
8 Basics of DMT - Discrete Multitone Transmission
9 DMT realization with IDFT/DFT
10 Exercises for the chapter

Possible bandwidth allocations for xDSL

The xDSL specifications give operators a great deal of freedom with regard to allocation.

For the necessary directional separation of the xDSL signal transmission according to

downstream direction from the provider to the customer (downstream with the highest possible data rate),
upstream direction from the customer to the provider (upstream with mostly lower data rate)

two variants have been standardized for this purpose:

$\text{Definition:}$

In the Frequenzgetrenntlageverfahren the data streams for the two directions are transmitted in two separate frequency bands with the advantage that a simple filter is sufficient to separate the transmission directions, which simplifies the technical implementation.
In the Frequenzgleichlageverfahren the spectra of upstream and downstream overlap in a certain part. The separation is done here with the help of an echo cancellation circuit. Advantages of the method are the lower bandwidth requirement at higher (and thus more attenuated) frequencies, as well as a longer range.

Frequenzgetrennt- und Frequenzgleichlageverfahren

The graphic compares these two options.

Basically, the specifications leave it up to the developers/operators to decide,

to operate xDSL alone on the subscriber line, or
to allow mixed operation of xDSL with the telephone services POTS (Plain Old Telephone Service) or ISDN (Integrated Services Digital Network) ,
and thus to exclude or also occupy the lower frequency range occupied by the two telephone services for xDSL.

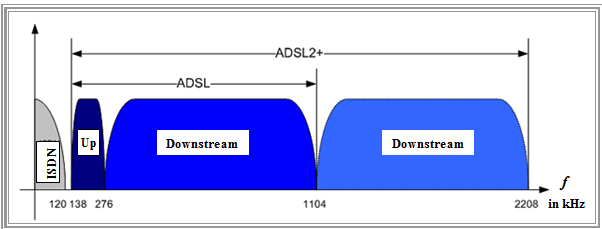
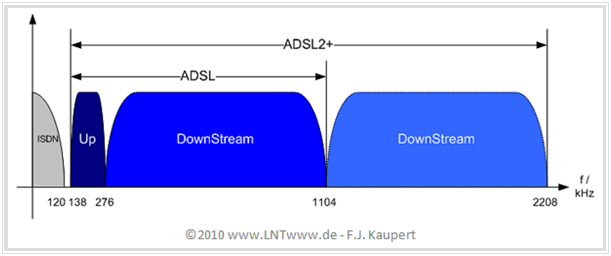
ADSL bandwidth allocation in Germany

Because it is technically much easier to implement, the decision was made in favor of ADSL and ADSL2+ in Germany.

ADSL bandwidth allocation in Germany

of the Frequenzgetrenntlageverfahren,
the general reservation of the lower frequency range for ISDN.

The Frequenzgleichlageverfahren is still used in some cases, but rather rarely.

For the transmission methods

"QAM" (quadrature amplitude modulation) and
"CAP" (Carrierless Amplitude Phase Modulation)

the bandwidth available for DSL is not further decomposed.

In contrast, in the multicarrier method "DMT" (Discrete Multitone Transmission), the uplink channel and the downlink channel are divided into $N_{\rm Up}$ respectively. $N_{\rm Down}$ bins of 4.3125 kHz each.
In addition to the above graph, it should be noted:

Phone services (POTS or ISDN) and xDSL are in different frequency bands, which minimizes mutual interference in the trunk cable. Thus, the stronger signal ISDN does not interfere with the parallel running xDSL and vice versa.
The lower frequency range up to $\text{120 kHz}$ has been reserved for ISDN (optionally POTS). This value results from the first zero of the "ISDN spectrum with 4B3T coding". Above $\text{120 kHz}$ the ISDN spectrum is completely suppressed.
To separate the telephone and xDSL signals, a "splitter" is used at both ends of the two-wire line, which includes one low-pass filter and one high-pass filter each and also takes into account the following frequency gap up to $\text{138 kHz}$ .
After this occupancy gap follows the ADSL upstream band from $\text{138 kHz}$ to $\text{276 kHz}$. This bandwidth allows the transmission of $N_{\rm Up} = 32$ subcarriers at $\text{4.3125 kHz}$ each. This value is derived from the frame transmission rate.
The subsequent downstream range extends to $\text{1104 kHz}$ for ADSL, with which $N_{\rm Down} = 256$ subcarriers can be realized. The separation of up and down channel in xDSL is done by a band-pass filter in the modem.
However, the first $64$ subcarriers $($this corresponds to $\text{276 kHz)}$ must not be occupied. With "Frequenzgleichlageverfahren" only $32$ subcarriers would have to be left out, taking into account that the separation of uplink and downlink requires a more complex implementation.
For ADSL2+, the system bandwidth is equal to $\text{2208 kHz}$ ⇒ $N_{\rm Down} = 512$ subcarriers. The number of bins to be spared remains unchanged compared to ADSL. Taking into account that two bins are occupied by control functions (e.g. for synchronization of transmitter and receiver), $190$ (ADSL) or $446$ (ADSL2+) downstream channels remain for users.
The ISDN reservation prescribed in Germany, however, has the consequence for xDSL that the low frequencies, which are by far the least attenuated in a copper line and would therefore actually be the most suitable, cannot be used.
Further, from the frequency arrangement, it can be seen that the downstream bins are more attenuated than the upstream bins (higher frequencies) and consequently have a smaller signal-to-noise ratio (SNR).
The decision "upstream below downstream" is related to the fact that the loss of downstream channels has only a comparatively small impact on the transmission rate. In the upstream, such a failure would be much more noticeable in percentage terms.

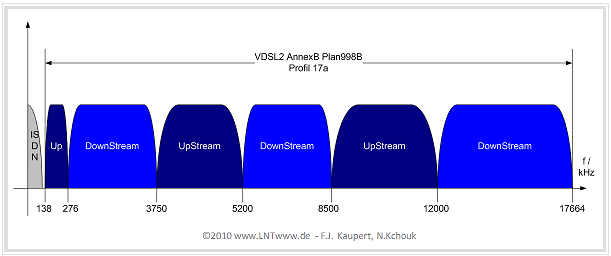
VDSL(2) bandwidth allocation

The ITU has defined several profiles for VDSL(2). At the time of writing this chapter (2010), the frequency band assignment specified in the graphic applies to the systems deployed in Germany in accordance with the ITU's VDSL(2) Plan 998b - Profile 17a (Annex B). The (slightly) lighter coloring at the higher frequencies is meant to indicate that these channels are more attenuated.

VDSL(2) bandwidth allocation in Germany

Without claiming to be exhaustive, this allocation plan can be characterized as follows:

To achieve higher bit rates, eight times as many bins are used here as in ADSL2+. Thus, the system bandwidth is $8 - \text{2208 MHz = 17664 MHz}$, enabling transmission rates of up to $\text{100 Mbit/s}$ (depending on cable length and condition).
Also here, the frequency bands for the upstream subchannels are always arranged at the lower frequencies, since the greater cable attenuation (increasing with frequency) has a greater percentage influence on the total bit rate for upstream than for downstream.
In VDSL(2) systems, the so-called "Frequenzgetrenntlageverfahren" is always used. Overlapping of the upstream and downstream frequency bands is categorically excluded in the ITU specification for VDSL(2).
In the VDSL systems in Germany, the lower frequencies are again reserved for ISDN. This is followed by alternating ranges for upstream and downstream. From the specified range limits, one can recognize the upstream ranges, which are narrower than the downstream.
You can see an alternating arrangement of upstream and downstream areas. One reason for this is that with this wide spectrum it should be avoided that one direction (for example downstream) is assigned only strongly attenuated (i.e. high) frequencies.
The VDSL(2) specification provides for allocation plans up to system bandwidths of $\text{30 MHz}$ (according to profile 30a), which should enable transmission rates up to about $\text{ 200 Mbit/s}$ over short distances. For this purpose, the bandwidth of the individual subchannels is also doubled compared to ADSL to $\text{8.625 kHz}$ .
All occupancy plans are provided with different masks for the power density spectrum in order to limit the maximum transmit power and thus the interference to neighboring systems in the cable bundle (crosstalk).

Overview of transmission methods

At the beginning of the various standardization procedures for the individual xDSL variants, different transmission methods were defined as a basis:

"Pulse Code Modulation (PCM)" for ISDN as well as Trellis Coded-Pulse Amplitude Modulation for HDSL2 and SHDSL/SDSL,
"Quadrature Amplitude Modulation (QAM)" for QAM-ADSL and QAM-VDSL,
"Carrierless Amplitude Phase Modulation (CAP)" for CAP-HDSL and CAP-ADSL,
"Discrete Multitone Transmission (DMT)" for ADSL, ADSL2, ADSL 2+, VDSL and VDSL2.

With increasing market demand for higher transmission rates and the associated requirements, two main suitable processes crystallized, namely $\rm QAM/CAP$ and $\rm DMT$.

Since the manufacturers were unable to agree on a common standard from 1997 to 2003, also for patent reasons (one even speaks of line code wars in this context), the two competing methods coexisted for a long time. At the so-called DSL Olympics in 2003, the decision was finally made in favor of DMT,

on the one hand because of the slightly better "performance" in general,
but in particular because of its higher robustness against narrowband interference.

Especially for the USA (many overhead telephone lines and related problems with coupled radio signals) the second argument played a major role.

The xDSL variants ADSL2(+) and VDSL(2), which are predominantly offered in Germany today (2010), are all based on the Discrete Multitone Transmission method, although the individual subcarriers may well be occupied by QAM signals.

First, however, the systems $\rm xDSL-QAM$ and $\rm xDSL-CAP$ will be considered very briefly.

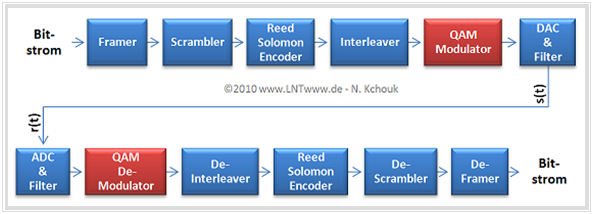
Basics of Quadrature Amplitude Modulation

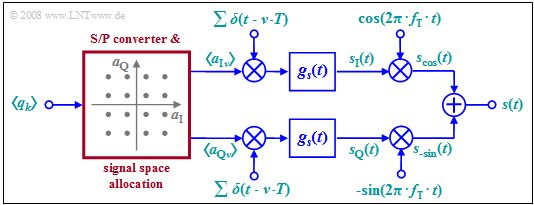
The diagram shows the reference model for ADSL-QAM, and here we will only deal with the red function blocks QAM modulator and QAM demodulator .

Reference model for ADSL QAM

The carrier frequency $f_{\rm T}$ is in each case within the specified uplink and downlink band of the respective xDSL variant. Like the signal space size (between four and 256 signal space points) and the symbol rate, it is determined by channel measurements during initialization of the transmission.

For ADSL QAM, the following symbol rates $($in ${\rm kBaud} = 1000 \rm symbols/s)$ have been specified:

model of quadrature amplitude modulation

$20$, $40$, $84$, $100$, $120$, $136$ upstream,
$40$, $126$, $160$, $252$, $336$, $504$, $806.4$, $1008$ in the downstream.

The principle has already been described in detail in the chapter "Quadrature Amplitude Modation" of the book "Modulation Methods".

Here follows only a short summary on the basis of the lower diagram.

QAM is a single carrier modulation method around the carrier frequency $f_{\rm T}$. First, a blockwise serial/parallel conversion of the bit stream and signal space assignment is performed.
From each $b$ binary symbol, two multilevel amplitude coefficients $a_{{\rm I}n}$ and $a_{{\rm Q}n}$ are derived (in-phase and quadrature components), where both coefficients can each take one of $M = 2^{b/2}$ possible amplitude values.
The example considered in the graph applies to the $\text{16-QAM}$ with $b = M = 4$ and correspondingly $16$ signal space points. For a $\text{256-QAM}$ $b = 8$ and $M = 16$ would hold $(2^b = M^2 = 256)$.
The coefficients $a_{{\rm I}n}$ and $a_{{\rm Q}n}$ are each impressed on a Dirac delta pulse as weights. For pulse shaping one usually uses (because of the small bandwidth) a raised-cosine filter. With the basic transmitted pulse $g_s(t)$ is then valid in the two branches of the block diagram:

$$ s_{\rm I}(t) = \sum_{n = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it n} \cdot g_s (t - n \cdot T)\hspace{0.05cm},\hspace{0.5cm} s_{\rm Q}(t) = \sum_{n = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it n} \cdot g_s (t - n \cdot T)\hspace{0.05cm}.$$

Note also that because of the redundancy-free conversion to a higher-level code, the symbol duration $T$ of these signals is greater by a factor $b$ than the bit duration $T_{\rm B}$ of the binary input sequence. In the drawn example (16-QAM), $T = 4 ⋅ T_{\rm B}$.
The QAM transmitting signal $s(t)$ is then the sum of the two partial signals multiplied by cosine and minus-sine, respectively (possibly followed by a band limit to prevent interference to adjacent bands, as indicated in the graph below):

$$s(t) = s_{\rm I}(t) \cdot \cos (2 \pi f_{\rm T}\,t) - s_{\rm Q}(t) \cdot \sin (2 \pi f_{\rm T}\,t) \hspace{0.05cm}. $$

The two branches $(\rm I$ and $\rm Q)$ can be considered as two completely separate $M$-level "ASK systems" which do not interfere with each other as long as all components are optimally designed.
This means at the same time: Compared to a "Binary Phase Shift Keying" (BPSK: modulation with cosine or sine only), the quadrature amplitude modulation allows a doubling of the data rate at constant quality.

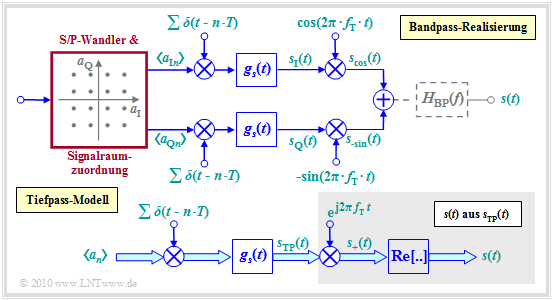
Quadrature Amplitude Modulation as band-pass and low-pass model

The last graph shows.

above the band-pass model,
below the equivalent low-pass model.

In this one, the inphase and quadrature coefficients are combined to give the complex amplitude coefficient

$$a_n = a_{\text{I}n} + {\rm j} ⋅ a_{\text{Q}n}$$

and additionally replaces the C-signal $s(t)$ by the equivalent low-pass signal

$$s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} ⋅ s_{\rm Q}(t).$$

The representation of the QAM transmitter and the QAM receiver is the content of the flash animation "Principle of Quadrature Amplitude Modulation".

$\text{Conclusion:}$

As the number of bits $b$ and thus the number of defined symbols $(M^2)$ increases, the bandwidth efficiency increases, but the signal processing overhead also increases.
In addition, it must be taken into account that a dense QAM allocation is appropriate only if the channel is sufficiently good.

Possible QAM signal space constellations

We still consider possible arrangements of signal space points in quadrature amplitude modulation using three examples.

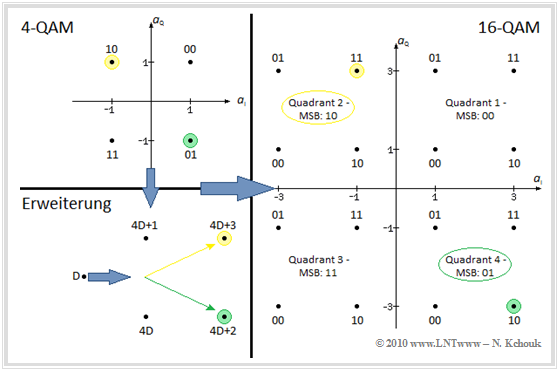
$\text{Example 1:}$ An important QAM parameter is the number of bits $b$ processed to the amplitude coefficient pair $(a_{\rm I}, a_{\rm Q})$ . Here $b$ is always even.

Signalraumkonstellationen $\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ und $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$

If $b = 2$, both $a_{\rm I}$ and $a_{\rm Q}$ can only take the values $±1$ resulting in the $\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ corresponding to the left constellation.

According to an ITU recommendation, the assignment applies here:

$$q_1 = 0, \ q_0 = 0 \, \Leftrightarrow \,a_{\rm I} = +1, \ a_{\rm Q} = +1,$$

$$q_1 = 0, \ q_0 = 1 \, \Leftrightarrow \, a_{\rm I} = +1, \ a_{\rm Q} = -1,$$

$$q_1 = 1, \ q_0 = 0 \, \Leftrightarrow \,a_{\rm I} = -1, \ a_{\rm Q} = +1,$$

$$q_1 = 1, \ q_0 = 1 \, \Leftrightarrow \, a_{\rm I} = -1, \ a_{\rm Q} = -1.$$

The point marked in yellow 10 $(a_{\rm I} = -1, \ a_{\rm Q} = 1)$ thus stands for $q_1 = 1$ and $q_0 = 0$.

With $b = 4$ ⇒ $M = 2^{b/2} = 4$ one arrives at $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$ according to the right diagram with the possible amplitude coefficients

$$a_{\rm I} ∈ \{±3, ±1\}, \ \ a_{\rm Q} ∈ \{±3, ±1\}.$$

The assignment can be determined using the auxiliary graph given on the left below, as illustrated by the following numerical examples.

$\rm (A)$ $q_3 = 1, \ q_2 = 0, \ q_1 = 1,\ q_0 = 1$ (yellow marker):

The two most significant bits (Most Significant Bit, MSB) 10 determine, according to the $\rm 4-QAM$ diagram, the quadrant in which the symbol is located.
The two least significant bits (11) together with the auxiliary graph determine the point within the quadrant. The result is $a_{\rm I} = -1$, $a_{\rm Q} = +3$.

$\rm (B)$ $q_3 = 0, \ q_2 = 1, \ q_1 = 1,\ q_0 = 0$ (green mark):

The two most significant bits (Most Significant Bit, MSB) 01 here refer to the fourth quadrant.
The two least significant bits (10) refer to the green dot in the fourth quadrant: $a_{\rm I} = -3, \ a_{\rm Q} = -3$.

$\text{Example 2:}$

Signal space constellations $\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ and $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$

The decimal value $D$ provides another way to label the points.

The yellow marked point in the $\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ diagram is binary labeled 10 ⇒ decimal $D = 2$. This point simultaneously marks the quadrant of $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$.
The further subdivision results from the lower left graphic. There at the yellow dot $4D + 3$ ⇒ 11 (decimal) is written. Therefore, the upper right dot (highlighted in yellow) in the upper left quadrant stands for decimal $11$ ⇒ binary 1011.

For the green dot, $D = 1$ gives the decimal value $4D + 2 ⇒ 6$, which corresponds to the binary representation 0110 .

According to this scheme, the signal space constellations for $\rm 64\hspace{0.05cm}–\hspace{-0.02cm}QAM$ ⇒ $(b = 6, \ M = 8)$ and $\rm 256-QAM$ ⇒ $(b = 8, \ M = 16)$ which will be discussed in detail in the "Exercise 2.3"

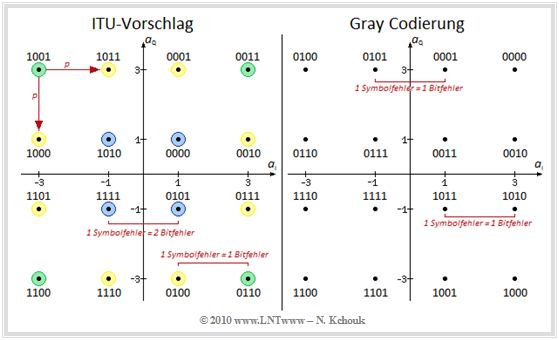
Zur Fehlerwahrscheinlichkeit bei $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$

$\text{Example 3:}$ We still consider for the described $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$ (left graph, here referred to as ITU proposal) the resulting error probability in the presence of AWGN noise:

An error can be assumed to result in a horizontally or vertically adjacent symbol, as indicated for the upper left (green) dot.
The error probability $p$ depends on the Euclidean distance of the two points and the AWGN noise power density $N_0$ .
A distortion to the more distant blue point instead of one of the two neighboring yellow points is rather unlikely with Gaussian noise.

All corner points (green background) can only be distorted in two directions. In contrast, the inner QAM points (blue background) have four direct neighbors and the remaining symbols (yellow background) have three. For the (average) symbol error probability then holds:

$$p_{\rm S} = {1}/{16} \cdot (4 \cdot 2 p + 8 \cdot 3 p + 4 \cdot 4 p) = 3p.$$

To calculate the bit error probability $p_{\rm B}$ it must now be taken into account that for the left constellation a symbol error

leads to only one bit error (example: 0100 ⇒ 0110, within one quadrant) or
to two bit errors (example: 1111 ⇒ 0101, between adjacent quadrants).

The computation of $p_{\rm B} $ here involves some effort.

In contrast, in a Gray encoding (right diagram), each symbol differs from its neighbors by exactly one bit, and each symbol error thus results in exactly one bit error. Since each individual symbol contains four bits, the (average) bit error probability in this case is:

$$p_{\rm B} = p_{\rm S}/4 = 3/4 \cdot p. $$

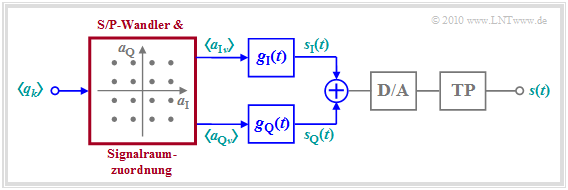
Carrierless Amplitude Phase Modulation (CAP)

Carrierless Amplitude Phase Modulation (CAP) is a bandwidth-efficient variant of QAM, which can be realized very easily with digital signal processors. The only difference to QAM is that modulation with a carrier signal can be omitted.

Model of Carrierless Amplitude Phase Modulation

Instead of multiplication by cosine and the negative sine, digital filtering is used here. $g_{\rm I}(t)$ and $g_{\rm Q}(t)$ are the phase-shifted impulse responses of two transversal bandpass filters with the same amplitude characteristics by $π/2$ .
Both are orthogonal to each other, which means that the integral of the product $g_{\rm I}(t) · g_{\rm Q}(t)$ over a symbol duration gives zero.
The signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ generated in this way are combined, converted to a continuous-time signal by a D/A converter, and the unwanted high-frequency components generated during D/A conversion are eliminated by a low-pass filter before transmission.
At the receiver, the signal $r(t)$ is first converted to a discrete-time signal using an A/D converter and then the in-phase and quadrature symbols $a_{\rm I}$ and $a_{\rm Q}$ are extracted via two finite impulse response (FIR) filters and downstream decision makers.

Reference model for CAP ADSL

CAP was the de facto standard in initial ADSL specifications until 1996.

The frequencies up to $\text{4 kHz}$ were reserved for POTS.
The up channel occupied the frequency range of $\text{15 - 160 kHz}$,
and the down channel occupied the frequencies from $\text{240 kHz}$ to $\text{1.5 MHz}$.
The graph shows the reference model.

One problem with CAP is that a "bad channel" has dramatic consequences on the transmission quality. Therefore, today (2010) CAP-ADSL is only found in a few HDSL variants.

Basics of DMT - Discrete Multitone Transmission

Discrete Multitone Transmission (DMT) refers to a multicarrier modulation method that is almost identical to "Orthogonal Frequency Division Multiplexing' (OFDM). In the case of wired transmission, one usually refers to "DMT", and in the case of wireless transmission, one refers to "OFDM".

In both cases, one divides the entire bandwidth into many narrowband equidistant subchannels. The respective subcarrier signals $s_k(t)$ are individually impinged with complex data symbols $D_k$ and the sum of the modulated subcarrier signals is transmitted as transmit signal $s(t)$ .

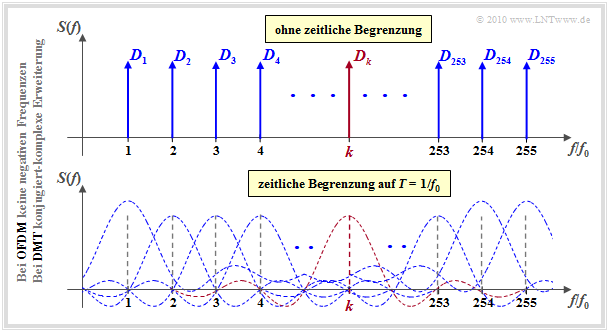
The diagram illustrates the principle of OFDM and DMT in the frequency domain, partly using the values specified for ADSL/DMT:

Spectra at OFDM and DMT

$255$ Subcarriers with carrier frequencies $k - f_0$ $(k = 1$, ... , $255)$.
Basic frequency $f_0 = 4.3125 \ \rm kHz$, since $4000$ data frames are transmitted per second.
After $68$ data frames, one synchronization frame is inserted each time.
Due to the cyclic prefix (see chapter [[Examples_of_Communication_Systems/Methods_to_Reduce_the_Bit_Error_Rate_in_DSL#Insert.C3.BCgen_of_Guard.E2.80.93Interval_and_cyclic_Pr. C3.A4fix|"Insertion of Guard–Interval and Cyclic Prefix"]) the symbol duration $T = 1/f_0$ must still be shortened by the factor $16/17$ .

An essential difference between OFDM and DMT is that.

in OFDM the represented spectrum $S(f)$ in reality describes an equivalent low-pass spectrum $S_{\rm TP}(f)$ and still the shift around a carrier frequency $f_{\rm T}$ has to be considered:

$$S_{\rm TP}(f ) = \sum_{k = 1}^{255} D_k \cdot \delta (f - k \cdot f_0)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} S(f) = \frac{1}{2} \big [ S_{\rm TP}(f - f_{\rm T}) + S^*_{\rm TP}(-(f + f_{\rm T}))\big ] \hspace{0.05cm},$$

in DMT, on the other hand, the components at negative frequencies must still be taken into account, which are to be weighted with the conjugate-complex spectral coefficients:

$$S(f ) = \sum_{k = 1}^{255} \big [ D_k \cdot \delta (f - k \cdot f_0) + D^*_k \cdot \delta (f + k \cdot f_0) \big ] \hspace{0.05cm}.$$

$\text{Please note:}$

According to these equations, the complex OFDM signal $s_{\rm OFDM}(t)$ consists of $K = 255$ complex exponential oscillations.
The DMT signal $s_{\rm DMT}(t)$ is composed of as many cosine oscillations with frequencies $k · f_0$ (full occupancy presupposed).
Despite complex coefficients $D_k$ resulting from QAM occupancy of the carriers, the DMT signal is always real at negative frequencies because of the conjugate-complex complements.

However, in both OFDM and DMT, the transmitted signal $s(t)$ is precisely limited in time to the symbol duration $T = 1/f_0 ≈ 232 \ {\rm µs}$ which is equivalent to multiplying by a square of duration $T$ . In the spectral domain, this corresponds to convolution with a slit function $\text{si}(πfT)$:

Each Dirac function at $k · f_0$ thus becomes an si function at the same position, given the time limit, as shown in the diagram below.
Adjacent subcarrier spectra overlap on the frequency axis, but exactly at $k · f_0$ the coefficients $D_k$ can be seen again, since all other spectra have zeros here.
For the lower graph a symmetrical rectangle is assumed. A rectangle between $0$ and $T$ would still result in a phase term. However, nothing would change with respect to $|S(f)|$ .

$\text{Example 4:}$ Assuming the conditions favorable for ADSL downstream, viz.

$4000$ frames are transmitted per second,
all subcarriers are active at all times $(K = 255)$,
each carrier is occupied with a 1024-QAM $(b = 10$, according to ITU $8 ≤ b ≤ 15 )$ and
ideal conditions prevail, so that the orthogonality evident in the graph is preserved,

then for the maximum data (bit)rate $R_{\rm B,\ max} = 4000 · K · b ≈ 10 \ \rm Mbit/s$.

However, specified ADSL downstream is only $2 \ \rm Mbit/s$ due to.

the omission of the $64$ lowest carriers because of ISDN and upstream,
the QAM occupancy of the heavily attenuated carriers with less than $10$ bits, and
the consideration of the cyclic prefix, and some operational reasons.

DMT realization with IDFT/DFT

MT system

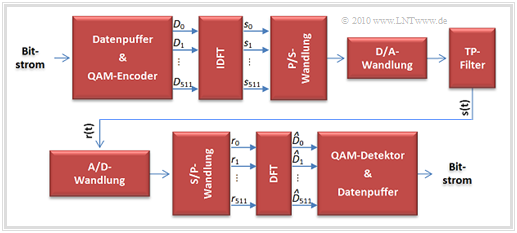
The upper graphic shows the complete DMT system, and we will focus on the two red blocks for now. The blue blocks will be covered in the "next chapter".

DMT transmitter and receiver

Simplified, the transmitter and receiver can be represented as shown in the left graphic:

To perform DMT modulation, the transmitter accumulates a block of input bits in a data buffer to be transmitted as one frame.
The QAM coder supplies per frame the complex-valued data symbols $D_1$, ... , $D_{255}$, which are assigned $D_0 = D_{256} = 0$ and $D_k = D^\star_{512-k} \ (k = 257,$ ... , $511)$ is expanded to the vector $\mathbf{D}$ of length $512$.
As a consequence "finite signals" are $D_{257}$, ... , $D_{511}$ identical to $D_{-255}$, ... , $D_{-1}$.
The spectral samples $\mathbf{D}$ are transformed by means of the "Inverse Discrete Fourier Transform" (IDFT) converted to the vector $\mathbf{s}$ of time signal samples, also with length $512$. Because of the conjugate-complex assignment in the spectral domain $\text{Im}[\mathbf{s}] = 0$.

After parallel/serial and digital/analog conversion and low-pass filtering of $\text{Re}[\mathbf{s}]$ the physical and thus real as well as continuous-time transmitted signal $s(t)$ results. For this, in the range $0 ≤ t ≤ T$ (factor $2$, since two coefficients each contribute to cosine/sine):

$$s(t) = \sum_{k = 1}^{255} \big [ 2 \cdot{\rm Re}\{D_k\} \cdot \cos(2\pi \cdot k f_0 \cdot t ) - 2 \cdot{\rm Im}\{D_k\} \cdot \sin(2\pi \cdot k f_0 \cdot t )\big ] \hspace{0.05cm}. $$

The received signal when transmitted over the AWGN channel is $r(t) = s(t) + n(t)$. After A/D and S/P conversion, $r(t)$ can be expressed by the (real) vector $\mathbf{r}$ . The "Discrete Fourier Transform" (DFT) then provides estimates for the transmitted spectral coefficients.

Allocation of the DMT frequency band with QAM coefficients

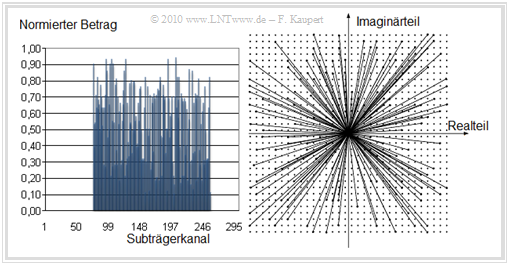
$\text{Examples 5:}$ As an example, let's consider the ADSL/DMT downstream.

In the upper left graph you can see the amounts $\vert D_k\vert $ of the occupied subchannels $64$, ... , $255$. The carriers $0$, ... , $63$ for the reserved frequency range of ISDN and upstream are set to zero.
To the right are the spectral coefficients $D_{64}$, ... , $D_{255}$ are shown in the complex number plane, where the signal space is chosen very large.

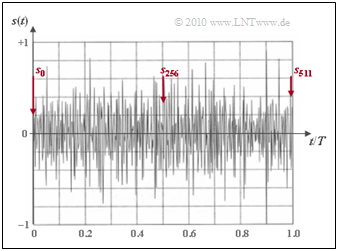
Transmitted signal with above DMT allocation

The second (left) graph shows the transmitted signal $s(t)$ for the frame duration $T = {1}/{f_0} ≈ 232 \ \rm µs$, which is obtained by low-pass filtering the IDFT values $s_0$, ... , $s_{511}$ results. This useful signal looks almost like noise. It can be seen:

The main problem of DMT is the unfavorable crest factor ⇒ the ratio of maximum value $s_{\rm max}$ and rms value $s_{\rm eff}$ (root of the average power).
The large dynamic range visible in the exemplary signal curve places high demands on the linearity of the amplifiers.
When the dynamic range is limited, the peaks of $s(t)$ are cut off.
This acts as an impulse interference and an additional noise load to the system.

$\text{Summarizing:}$

Discrete Multitone Transmission (DMT) is basically the parallel implementation of many narrowband QAM modems with different carriers and relatively low data transmission rates. The low bandwidth per subcarrier allows a long symbol duration, thus reducing the influence of intersymbol interference and reducing the development effort for equalization.
A major reason for the success of DMT is its technical ease of implementation. IDFT and DFT are formed with digital signal processors in real time. The vectors have the length $512$ (power of two). Therefore the particularly fast FFT algorithm (Fast Fourier Transformation) can be applied.