Error Probability for Baseband Transmission

1. Digital Signal Transmission
2. Digitalsignalübertragung bei idealisierten Bedingungen
3. Error Probability for Baseband Transmission

• Previous page
• Next page

• Previous page
• Next page

Definition der Bitfehlerwahrscheinlichkeit

Zur Definition der Bitfehlerwahrscheinlichkeit

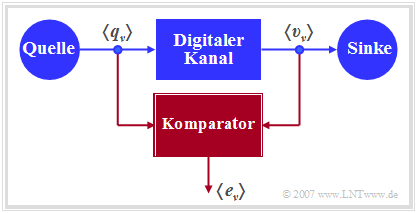
Die Grafik zeigt ein sehr einfaches, aber allgemeingültiges Modell eines binären Übertragungssystems. Dieses lässt sich wie folgt charakterisieren:

• Quelle und Sinke werden durch die beiden Binärfolgen  $〈q_ν〉$  und  $〈v_ν〉$  beschrieben.
• Das gesamte Übertragungsystem – bestehend aus Sender, Übertragungskanal inklusive Störungen und Empfänger – wird als „Black Box” mit binärem Eingang und binärem Ausgang betrachtet.
• Dieser „Digitale Kanal” wird allein durch die Fehlerfolge $〈e_ν〉$ charakterisiert. Bei fehlerfreier Übertragung des $\nu$–ten Bits  $(v_ν = q_ν)$  gilt  $e_ν= 0$, andernfalls  $(v_ν \ne q_ν)$  wird  $e_ν= 1$  gesetzt.

$\text{Definition:}$  Die (mittlere) Bitfehlerwahrscheinlichkeit ist bei einem Binärsystem wie folgt gegeben:

$$p_{\rm B} = {\rm E}\big[{\rm Pr}(v_{\nu} \ne q_{\nu})\big]= \overline{ {\rm Pr}(v_{\nu} \ne q_{\nu}) } = \lim_{N \to\infty}\frac{1}{N}\cdot\sum\limits_{\nu=1}^{N}{\rm Pr}(v_{\nu} \ne q_{\nu})\hspace{0.05cm}.$$

Diese statistische Größe ist das wichtigste Beurteilungskriterium eines jeden Digitalsystems.

• Die Berechnung als Erwartungswert  $\rm E[\text{...}]$  gemäß dem ersten Teil der obigen Gleichung entspricht einer Scharmittelung über die Verfälschungswahrscheinlichkeit  ${\rm Pr}(v_{\nu} \ne q_{\nu})$  des  $\nu$–ten Symbols, während die überstreichende Linie im rechten Gleichungsteil eine Zeitmittelung kennzeichnet.

• Beide Berechnungsarten führen – unter der gerechtfertigten Annahme ergodischer Prozesse – zum gleichen Ergebnis, wie im vierten Hauptkapitel „Zufallsgrößen mit statistischen Bindungen” des Buches  Stochastische Signaltheorie  gezeigt wurde.

• Auch aus der Fehlerfolge  $〈e_ν〉$  lässt sich die Bitfehlerwahrscheinlichkeit als Erwartungswert bestimmen, wobei zu berücksichtigen ist, dass die Fehlergröße  $e_ν$  nur die Werte  $0$  und  $1$  annehmen kann:

$$\it p_{\rm B} = \rm E\big[\rm Pr(\it e_{\nu}=\rm 1)\big]= {\rm E}\big[{\it e_{\nu}}\big]\hspace{0.05cm}.$$

• Die obige Definition der Bitfehlerwahrscheinlichkeit gilt unabhängig davon, ob es statistische Bindungen innerhalb der Fehlerfolge  $〈e_ν〉$  gibt oder nicht. Je nachdem muss man bei einer Systemsimulation unterschiedliche digitale Kanalmodelle verwenden. Der Aufwand zur  $p_{\rm B}$–Berechnung hängt hiervon ab.

Im fünften Hauptkapitel wird gezeigt, dass das so genannte  BSC–Modell  (Binary Symmetrical Channel) statistisch unabhängige Fehler liefert, während für die Beschreibung von Bündelfehlerkanälen auf die Modelle von  Gilbert–Elliott  [Gil60] und von  McCullough  [McC68] zurückgegriffen werden muss.

Definition der Bitfehlerquote

Die Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  eignet sich zum Beispiel gut für die Konzipierung und Optimierung von Digitalsystemen. Diese ist eine  Apriori-Kenngröße, die eine Vorhersage über das Fehlerverhalten eines Nachrichtensystems erlaubt, ohne dass dieses bereits realisiert sein muss.

Dagegen muss zur messtechnischen Erfassung der Qualität eines realisierten Systems oder bei einer Systemsimulation auf die Bitfehlerquote übergegangen werden, die durch den Vergleich von Quellensymbolfolge  $〈q_ν〉$  und Sinkensymbolfolge  $〈v_ν〉$  ermittelt wird. Diese ist somit eine  Aposteriori-Kenngröße des Systems.

$\text{Definition:}$  Die Bitfehlerquote (englisch: Bit Error Rate, BER) ist das Verhältnis aus der Anzahl  $n_{\rm B}(N)$  der aufgetretenen Bitfehler  $(v_ν \ne q_ν)$  und der Anzahl  $N$  der insgesamt übertragenen Symbole:

$$h_{\rm B}(N) = \frac{n_{\rm B}(N)}{N} \hspace{0.05cm}.$$

Im Sinne der Wahrscheinlichkeitsrechnung ist die Bitfehlerquote eine  relative Häufigkeit; sie wird deshalb auch Bitfehlerhäufigkeit genannt.

• Die Schreibweise  $h_{\rm B}(N)$  soll deutlich machen, dass die per Messung oder durch Simulation ermittelte Bitfehlerquote signifikant von dem Parameter  $N$ – also der Anzahl der insgesamt übertragenen oder simulierten Symbole – abhängt.
• Nach den elementaren Gesetzen der Wahrscheinlichkeitsrechnung stimmt nur im Grenzfall  $N \to \infty$  die Aposteriori–Kenngröße  $h_{\rm B}(N)$  mit der Apriori–Kenngröße  $p_{\rm B}$  exakt überein.
  
  

Der Zusammenhang zwischen Wahrscheinlichkeit und relativer Häufigkeit wird im Lernvideo Bernoullisches Gesetz der großen Zahlen verdeutlicht.

Bitfehlerwahrscheinlichkeit und Bitfehlerquote beim BSC-Modell

Für die nachfolgenden Herleitungen wird das BSC–Modell (Binary Symmetric Channel ) zugrunde gelegt, das in   Kapitel 5.2  im Detail beschrieben wird.

• Jedes Bit wird mit der Wahrscheinlichkeit  $p = {\rm Pr}(v_{\nu} \ne q_{\nu}) = {\rm Pr}(e_{\nu} = 1)$  verfälscht, unabhängig von den Fehlerwahrscheinlichkeiten der benachbarten Symbole.
• Die (mittlere) Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  ist somit ebenfalls gleich  $p$.

Nun wird abgeschätzt, wie genau beim BSC-Modell die Bitfehlerwahrscheinlichkeit  $p_{\rm B} = p$  durch die Bitfehlerquote  $h_{\rm B}(N)$  approximiert wird:

• Die Anzahl der Bitfehler bei der Übertragung von  $N$  Symbolen ist eine diskrete Zufallsgröße:

$$n_{\rm B}(N) = \sum\limits_{\it \nu=\rm 1}^{\it N} e_{\nu} \hspace{0.2cm} \in \hspace{0.2cm} \{0, 1, \hspace{0.05cm}\text{...} \hspace{0.05cm} , N \}\hspace{0.05cm}.$$

• Bei statistisch unabhängigen Fehlern (BSC–Modell) ist  $n_{\rm B}(N)$  binominalverteilt. Demzufolge gilt für Mittelwert und Streuung dieser Zufallsgröße:

$$m_{n{\rm B}}=N \cdot p_{\rm B},\hspace{0.2cm}\sigma_{n{\rm B}}=\sqrt{N\cdot p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}\hspace{0.05cm}.$$

• Für Mittelwert und Streuung der Bitfehlerquote  $h_{\rm B}(N)= n_{\rm B}(N)/N$  gilt deshalb:\[m_{h{\rm B}}= \frac{m_{n{\rm B}}}{N} = p_{\rm B}\hspace{0.05cm},\hspace{0.2cm}\sigma_{h{\rm B}}= \frac{\sigma_{n{\rm B}}}{N}= \sqrt{\frac{ p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}{N}}\hspace{0.05cm}.\]
• Nach  Moivre  und  Laplace  kann aber die Binominalverteilung näherungsweise durch eine Gaußverteilung approximiert werden:

$$f_{h{\rm B}}({h_{\rm B}}) \approx \frac{1}{\sqrt{2\pi}\cdot\sigma_{h{\rm B}}}\cdot {\rm e}^{-(h_{\rm B}-p_{\rm B})^2/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{h{\rm B}}^2)}.$$

• Mit dem  Gaußschen Fehlerintergal  ${\rm Q}(x)$  lässt sich so die Wahrscheinlichkeit  $p_\varepsilon$  berechnen, dass die per Simulation/Messung über  $N$  Symbole ermittelte Bitfehlerquote  $h_{\rm B}(N)$  betragsmäßig um weniger als einen Wert  $\varepsilon$  von der tatsächlichen Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  abweicht:

$$p_{\varepsilon}= {\rm Pr} \left( |h_{\rm B}(N) - p_{\rm B}| < \varepsilon \right) = 1 -2 \cdot {\rm Q} \left( \frac{\varepsilon}{\sigma_{h{\rm B}}} \right)= 1 -2 \cdot {\rm Q} \left( \frac{\varepsilon \cdot \sqrt{N}}{\sqrt{p_{\rm B} \cdot (1-p_{\rm B})}} \right)\hspace{0.05cm}.$$

$\text{Fazit:}$  Dieses Ergebnis ist wie folgt zu interpretieren:

• Führt man unendlich viele Versuchsreihen über jeweils  $N$  Symbole durch, ist der Mittelwert  $m_{h{\rm B} }$  tatsächlich gleich der gesuchten Fehlerwahrscheinlichkeit  $p_{\rm B}$.
• Bei einer einzigen Versuchsreihe wird man dagegen nur eine Näherung erhalten, wobei die jeweilige Abweichung vom Sollwert bei mehreren Versuchsreihen gaußverteilt ist.

$\text{Beispiel 1:}$  Die Bitfehlerwahrscheinlichkeit betrage  $p_{\rm B}= 10^{-3}$  und es ist bekannt, dass die Bitfehler statistisch unabhängig sind.

• Macht man nun sehr viele Versuchsreihen mit jeweils  $N= 10^{5}$  Symbolen, so werden die jeweiligen Ergebnisse  $h_{\rm B}(N)$  entsprechend einer Gaußverteilung um den Sollwert  $10^{-3}$  variieren.
• Die Streuung beträgt dabei  $\sigma_{h{\rm B} }= \sqrt{ { p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}/{N} }\approx 10^{-4}\hspace{0.05cm}.$
• Die Wahrscheinlichkeit, dass die relative Häufigkeit einen Wert zwischen  $0.9 \cdot 10^{-3}$  und  $1.1 \cdot 10^{-3}$  haben wird   $(\varepsilon=10^{-4})$, ist somit gleich

$$p_{\varepsilon} = 1 - 2 \cdot {\rm Q} \left({\varepsilon}/{\sigma_{h{\rm B} } } \right )= 1 - 2 \cdot {\rm Q} (1) \approx 68.4\%.$$

• Soll diese Wahrscheinlichkeit (Genauigkeit) auf  $95\%$  gesteigert werden, so wären  $N = 400\hspace{0.05cm}000$  Symbole erforderlich.

Fehlerwahrscheinlichkeit bei Gaußschem Rauschen

Entsprechend den   Voraussetzungen zu diesem Kapitel  gehen wir von folgenden Annahmen aus:

• Das Detektionssignal zu den Detektionszeitpunkten kann wie folgt dargestellt werden:   $ d(\nu T) = d_{\rm S}(\nu T)+d_{\rm N}(\nu T)\hspace{0.05cm}. $
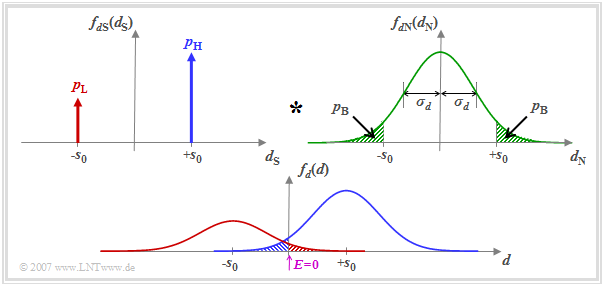
• Der Nutzanteil wird durch die Wahrscheinlichkeitsdichtefunktion (WDF)  $f_{d{\rm S}}(d_{\rm S}) $  beschrieben, wobei wir hier von unterschiedlichen Auftrittswahrscheinlichkeiten  $p_{\rm L} = {\rm Pr}(d_{\rm S} = -s_0)$  und  $p_{\rm H} = {\rm Pr}(d_{\rm S} = +s_0)= 1-p_{\rm L}$  ausgehen.
• Die WDF  $f_{d{\rm N}}(d_{\rm N})$  der Störkomponente sei gaußförmig und besitze die Streuung  $\sigma_d$.

Fehlerwahrscheinlichkeit bei Gaußschem Rauschen

Unter der Voraussetzung, dass  $d_{\rm S}(\nu T)$  und  $d_{\rm N}(\nu T)$  statistisch unabhängig voneinander sind  („signalunabhängiges Rauschen”), ergibt sich die WDF  $f_d(d) $  der Detektionsabtastwerte  $d(\nu T)$  als das Faltungsprodukt

$$f_d(d) = f_{d{\rm S}}(d_{\rm S}) \star f_{d{\rm N}}(d_{\rm N})\hspace{0.05cm}.$$

Der Schwellenwertentscheider mit der Schwelle  $E = 0$  trifft immer dann eine falsche Entscheidung, wenn

• das Symbol  $\rm L$  gesendet wurde  $(d_{\rm S} = -s_0)$ und  $d > 0$  ist (rote schraffierte Fläche), oder
• das Symbol  $\rm H$  gesendet wurde  $(d_{\rm S} = +s_0)$ und  $d < 0$  ist (blaue schraffierte Fläche).

Da die Flächen der roten und der blauen Gaußkurven zusammen  $1$  ergeben, gibt die Summe aus der rot und der blau schraffierten Fläche die Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  an. Die beiden grün schraffierten Flächen in der oberen Wahrscheinlichkeitsdichtefunktion  $f_{d{\rm N}}(d_{\rm N})$  sind – jede für sich – ebenfalls gleich  $p_{\rm B}$.

Die anhand der Grafik veranschaulichten Ergebnisse sollen nun formelmäßig hergeleitet werden. Ausgegangen wird von der Gleichung

$$p_{\rm B} = p_{\rm L} \cdot {\rm Pr}( v_\nu = \mathbf{H}\hspace{0.1cm}|\hspace{0.1cm} q_\nu = \mathbf{L})+ p_{\rm H} \cdot {\rm Pr}(v_\nu = \mathbf{L}\hspace{0.1cm}|\hspace{0.1cm} q_\nu = \mathbf{H})\hspace{0.05cm}.$$

• Hierbei sind  $p_{\rm L} $  und  $p_{\rm H} $  die Quellensymbolwahrscheinlichkeiten. Die jeweils zweiten (bedingten) Wahrscheinlichkeiten  $ {\rm Pr}( v_\nu \hspace{0.05cm}|\hspace{0.05cm} q_\nu)$  beschreiben die Verfälschungen durch den AWGN–Kanal. Aus der Entscheidungsregel des Schwellenwertentscheiders  $($mit Schwelle  $E = 0)$  ergibt sich auch:

$$p_{\rm B} = p_{\rm L} \cdot {\rm Pr}( d(\nu T)>0)+ p_{\rm H} \cdot {\rm Pr}( d(\nu T)<0) =p_{\rm L} \cdot {\rm Pr}( d_{\rm N}(\nu T)>+s_0)+ p_{\rm H} \cdot {\rm Pr}( d_{\rm N}(\nu T)<-s_0) \hspace{0.05cm}.$$

• Die beiden Überschreitungswahrscheinlichkeiten in obiger Gleichung sind aufgrund der Symmetrie der Gaußschen WDF  $f_{d{\rm N}}(d_{\rm N})$  gleich. Es gilt:

$$p_{\rm B} = (p_{\rm L} + p_{\rm H}) \cdot {\rm Pr}( d_{\rm N}(\nu T)>s_0) = {\rm Pr}( d_{\rm N}(\nu T)>s_0)\hspace{0.05cm}.$$

Das bedeutet:   $p_{\rm B}$  hängt bei einem Binärsystem mit der Schwelle  $E = 0$  nicht von den Symbolwahrscheinlichkeiten  $p_{\rm L} $  und  $p_{\rm H} = 1- p_{\rm L}$  ab.

• Die Wahrscheinlichkeit, dass der AWGN–Rauschterm  $d_{\rm N}$  mit Streuung  $\sigma_d$  größer ist als die NRZ–Sendeimpulsamplitude  $s_0$, ergibt sich damit zu:

$$p_{\rm B} = \int_{s_0}^{+\infty}f_{d{\rm N}}(d_{\rm N})\,{\rm d} d_{\rm N} = \frac{\rm 1}{\sqrt{2\pi} \cdot \sigma_d}\int_{ s_0}^{+\infty}{\rm e} ^{-d_{\rm N}^2/(2\sigma_d^2) }\,{\rm d} d_{\rm N}\hspace{0.05cm}.$$

• Unter Verwendung des komplementären Gaußschen Fehlerintegrals  ${\rm Q}(x)$  lautet das Ergebnis:

$$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)\hspace{0.4cm}{\rm mit}\hspace{0.4cm}\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.$$

• Häufig – insbesondere in der englischsprachigen Literatur – wird anstelle von  ${\rm Q}(x)$  die vergleichbare komplementäre Error Function  ${\rm erfc}(x)$  verwendet. Mit dieser gilt:

$$p_{\rm B} = {1}/{2} \cdot {\rm erfc} \left( \frac{s_0}{\sqrt{2}\cdot \sigma_d}\right)\hspace{0.4cm}{\rm mit}\hspace{0.4cm} {\rm erfc} (\it x) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$

Beide Funktionen findet man in Formelsammlungen in tabellarischer Form. Sie können zur Berechnung der Funktionswerte von  ${\rm Q}(x)$  und  $1/2 \cdot {\rm erfc}(x)$  aber auch unser interaktives Applet  Komplementäre Gaußsche Fehlerfunktionen  benutzen.

$\text{Beispiel 2:}$  Für das Folgende wird vorausgesetzt, dass Tabellen zur Verfügung stehen, in denen das Argument der Gaußschen Fehlerfunktionen im Abstand  $0.1$  aufgelistet sind. Mit  $s_0/\sigma_d = 4$  erhält man für die Bitfehlerwahrscheinlichkeit gemäß der Q–Funktion:

$$p_{\rm B} = {\rm Q} (4) = 0.317 \cdot 10^{-4}\hspace{0.05cm}.$$

Nach der zweiten Gleichung ergibt sich:

$$p_{\rm B} = {1}/{2} \cdot {\rm erfc} ( {4}/{\sqrt{2} })= {1}/{2} \cdot {\rm erfc} ( 2.828)\approx {1}/{2} \cdot {\rm erfc} ( 2.8)= 0.375 \cdot 10^{-4}\hspace{0.05cm}.$$

• Richtig ist der erste Wert. Bei der zweiten Berechnungsart muss man runden oder – noch besser – interpolieren, was aufgrund der starken Nichtlinearität dieser Funktion sehr schwierig ist.
  
• Bei den gegebenen Zahlenwerten ist demnach die Q–Funktion besser geeignet. Außerhalb von Übungsbeispielen wird  $s_0/\sigma_d$  in der Regel einen „krummen” Wert besitzen. In diesem Fall bietet die Q–Funktion natürlich keinen Vorteil gegenüber  ${\rm erfc}(x)$.

Optimaler Binärempfänger - Realisierung mit Matched-Filter

Wir gehen weiter von den  vorne festgelegten Voraussetzungen  aus.

Optimaler Binärempfänger (Matched-Filter-Variante)

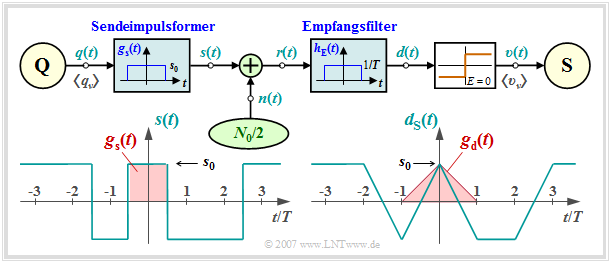
• Dann kann man für den Frequenzgang und die Impulsantwort des Empfängerfilters ansetzen:

$$H_{\rm E}(f) = {\rm si}(\pi f T) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ 1/(2T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |\hspace{0.05cm}t\hspace{0.05cm}|< T/2 \hspace{0.05cm},\\ |\hspace{0.05cm}t\hspace{0.05cm}|= T/2 \hspace{0.05cm},\\ |\hspace{0.05cm}t\hspace{0.05cm}|>T/2 \hspace{0.05cm}. \\ \end{array}$$

• Aufgrund der Linearität kann für das Detektionsnutzsignal  geschrieben werden:

$$d_{\rm S}(t) = \sum_{(\nu)} a_\nu \cdot g_d ( t - \nu \cdot T)\hspace{0.4cm}{\rm mit}\hspace{0.4cm}g_d(t) = g_s(t) \star h_{\rm E}(t) \hspace{0.05cm}.$$

• Die Faltung zweier Rechtecke gleicher Breite  $T$  und Höhe  $s_0$  ergibt einen dreieckförmigen Detektionsgrundimpuls  $g_d(t)$  mit  $g_d(t = 0) = s_0$. Wegen  $g_d(|t| \ge 0) \equiv 0$  ist das System impulsinterferenzfrei; es gilt  $d_{\rm S}(\nu T)= \pm s_0$.

• Die Varianz des Detektionsstörsignals  $d_{\rm N}(t)$ – also die Detektionsstörleistung – lautet:

$$\sigma _d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H_{\rm E}( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = \frac{N_0 }{2} \cdot \int_{- \infty }^{+ \infty } {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm{d}}f = \frac{N_0 }{2T} \hspace{0.05cm}.$$

• Damit ergeben sich für die Bitfehlerwahrscheinlichkeit entsprechend der letzten Seite die beiden äquivalenten Gleichungen:

$$p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot s_0^2 \cdot T}{N_0}}\right)= {\rm Q} \left( \sqrt{\rho_d}\right)\hspace{0.05cm},\hspace{0.5cm} p_{\rm B} = {1}/{2} \cdot {\rm erfc} \left( \sqrt{{ s_0^2 \cdot T}/{N_0}}\right)= {1}/{2}\cdot {\rm erfc}\left( \sqrt{{\rho_d}/{2}}\right) \hspace{0.05cm}.$$

$\text{Definition:}$  Verwendet ist das momentane Signal–zu–Stör–Leistungsverhältnis (SNR)  $\rho_d$   des Detektionssignals  $d(t)$  zu den Zeiten  $\nu T$, kurz Detektions–SNR:

$$\rho_d = \frac{d_{\rm S}^2(\nu T)}{ {\rm E}\big[d_{\rm N}^2(\nu T)\big ]}= \frac{s_0^2}{\sigma _d ^2} \hspace{0.05cm}.$$

Ein Vergleich dieses Ergebnisses mit der Seite   Optimierungskriterium des Matched-Filters  im Buch „Stochastische Signaltheorie” zeigt, dass das Empfangsfilter  $H_{\rm E}(f)$  ein an den Sendegrundimpuls  $g_s(t)$  angepasstes Matched–Filter ist:

$$H_{\rm E}(f) = H_{\rm MF}(f) = K_{\rm MF}\cdot G_s^*(f)\hspace{0.05cm}.$$

Gegenüber der Seite   Matched–Filter–Optimierung  sind hier folgende Modifikationen berücksichtigt:

• Die Matched–Filter–Konstante ist hier zu  $K_{\rm MF} = 1/(s_0 \cdot T)$  gesetzt. Damit ist der Frequenzgang  $ H_{\rm MF}(f)$  dimensionslos.
• Der im allgemeinen frei wählbare Detektionszeitpunkt ist hier zu  $T_{\rm D} = 0$  gewählt. Damit ergibt sich allerdings ein akausales Filter.
• Das Detektions–SNR kann für jeden beliebigen Sendegrundimpuls  $g_s(t)$  mit Spektrum  $G_s(f)$  wie folgt dargestellt werden, wobei sich die rechte Identität aus dem  Parsevalschen Theorem  ergibt:

$$\rho_d = \frac{2 \cdot E_{\rm B}}{N_0}\hspace{0.4cm}{\rm mit}\hspace{0.4cm} E_{\rm B} = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = \int^{+\infty} _{-\infty} |G_s(f)|^2\,{\rm d}f\hspace{0.05cm}.$$

• $E_{\rm B}$  wird oft als Energie pro Bit  bezeichnet und  $E_{\rm B}/N_0$ – fälschlicherweise – als  $\rm SNR$. Wie aus der letzten Gleichung ersichtlich ist, unterscheidet sich nämlich bei binärer Basisbandübertragung  $E_{\rm B}/N_0$  vom Detektions–SNR  $\rho_d$  um den Faktor  $2$.

$\text{Fazit:}$  Die hier hergeleitete Bitfehlerwahrscheinlichkeit des optimalen Binärempfängers kann somit auch wie folgt geschrieben werden:

$$p_{\rm B} = {\rm Q} \left( \sqrt{ {2 \cdot E_{\rm B} }/{N_0} }\right)= {1}/{2} \cdot{\rm erfc} \left( \sqrt{ {E_{\rm B} }/{N_0} }\right) \hspace{0.05cm}.$$

Diese Gleichung gilt sowohl für die Realisierung mit Matched-Filter als auch für die Realisierungsform „Integrate & Dump”  (siehe nächste Seite).

Zur Verdeutlichung der hier behandelten Thematik weisen wir auf unser Interaktionsmodul  Zur Verdeutlichung des Matched-Filters  hin.

Optimaler Binärempfänger – Realisierungsform „Integrate & Dump”

Bei rechteckförmigen NRZ–Sendeimpulsen kann das Matched–Filter auch als Integrator $($jeweils über eine Symboldauer  $T)$ realisiert werden. Damit gilt für das Detektionssignal zu den Detektionszeitpunkten:

$$d(\nu \cdot T + T/2) = \frac {1}{T} \cdot \int^{\nu \cdot T + T/2} _{\nu \cdot T - T/2} r(t)\,{\rm d}t \hspace{0.05cm}.$$

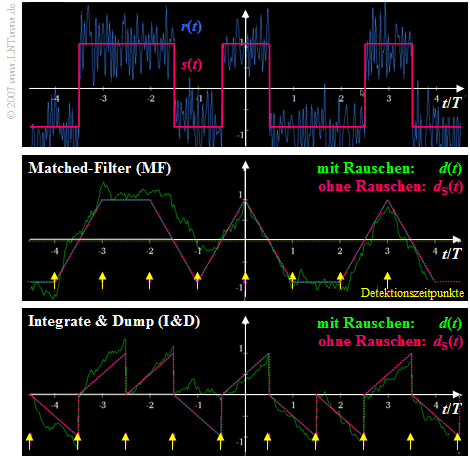
Die Grafik verdeutlicht die Unterschiede bei der Realisierung des optimalen Binärempfängers

• mit Matched–Filter $\rm (MF)$   ⇒   mittlere Skizze, bzw.
• als „Integrate & Dump” $\rm (I\&D)$   ⇒   untere Skizze.

Man erkennt aus diesen Signalverläufen:

• Das Detektionsnutzsignal  $d_{\rm S}(t)$  ist zu den Detektionszeitpunkten   ⇒   gelbe Markierungen $\rm (MF$:   bei  $\nu \cdot T$, $\rm I\&D$:   bei  $\nu \cdot T +T/2$  in beiden Fällen gleich $\pm s_0$.
• Die unterschiedlichen Detektionszeitpunkte sind darauf zurückzuführen, dass das Matched–Filter im Gegensatz zu „Integrate & Dump” als akausal angesetzt wurde (siehe letzte Seite).
• Beim Matched–Filter–Empfänger ist die Varianz des Detektionsstörsignals zu allen Zeiten  $t$  gleich:   ${\rm E}\big[d_{\rm N}^2(t)\big]= {\sigma _d ^2} = {\rm const.}$ Dagegen nimmt beim I&D–Empfänger die Varianz von Symbolanfang bis Symbolende zu.
• Zu den gelb markierten Zeitpunkten ist die Detektionsstörleistung in beiden Fällen gleich, so dass sich die gleiche Bitfehlerwahrscheinlichkeit ergibt. Mit  $E_{\rm B} = s_0^2 \cdot T$  gilt wieder:

$$\sigma _d ^2 = \frac{N_0}{2} \cdot \int_{- \infty }^{ +\infty } {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm{d}}f = \frac{N_0}{2T} $$

$$\Rightarrow \hspace{0.3cm} p_{\rm B} = {\rm Q} \left( \sqrt{ s_0^2 / \sigma _d ^2} \right)= {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right) .$$

Interpretation des optimalen Empfängers

In diesem Abschnitt wurde gezeigt, dass mit einem Empfänger, bestehend aus linearem Empfangsfilter und nichtlinearem Entscheider, die kleinstmögliche Bitfehlerwahrscheinlichkeit zu erreichen ist:

$$ p_{\rm B, \hspace{0.05cm}min} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right) = {1}/{2} \cdot {\rm erfc} \left( \sqrt{{ E_{\rm B}}/{N_0}}\right) \hspace{0.05cm}.$$

Die sich ergebende Konfiguration ist ein Sonderfall des so genannten Maximum–Aposteriori–Empfängers (MAP), der im Abschnitt  Optimale Empfängerstrategien  im dritten Hauptkapitel dieses Buches behandelt wird.

Für die Gültigkeit obiger Gleichung müssen allerdings eine Reihe von Voraussetzungen erfüllt sein:

• Das Sendesignal  $s(t)$  ist binär sowie bipolar (antipodisch) und weist pro Bit die (mittlere) Energie  $E_{\rm B}$  auf. Die (mittlere) Sendeleistung ist somit $E_{\rm B}/T$.
• Es liegt ein AWGN–Kanal (Additive White Gaussian Noise ) mit der konstanten (einseitigen) Rauschleistungsdichte  $N_0$  vor.
• Das Empfangsfilter  $H_{\rm E}(f)$  ist bestmöglich an das Sendegrundimpulsspektrum  $G_s(f)$  entsprechend dem „Matched–Filter–Kriterium” angepasst.
• Der Entscheider (Schwellenwert, Detektionszeitpunkte) ist optimal. Eine kausale Realisierung des Matched–Filters kann man durch Verschiebung des Detektionszeitpunktes ausgleichen.
• Obige Gleichung gilt unabhängig vom Sendegrundimpuls  $g_s(t)$. Allein die für die Übertragung eines Binärsymbols aufgewendete Energie  $E_{\rm B}$  ist neben der Rauschleistungsdichte  $N_0$  entscheidend für die Bitfehlerwahrscheinlichkeit  $p_{\rm B}$.
• Voraussetzung für die Anwendbarkeit obiger Gleichung ist, dass die Detektion eines Symbols nicht durch andere Symbole beeinträchtigt wird. Solche  Impulsinterferenzen  vergrößern die Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  enorm.
• Ist die absolute Sendeimpulsdauer  $T_{\rm S}$  kleiner oder gleich dem Symbolabstand  $T$, so ist obige Gleichung bei Erfüllung des Matched-Filter-Kriteriums immer anwendbar.
• Die Gleichung gilt auch für Nyquistsysteme, bei denen zwar  $T_{\rm S} > T$  gilt, es aber aufgrund von äquidistanten Nulldurchgängen des Grundimpulses  $g_d(t)$  nicht zu Impulsinterferenzen kommt. Damit beschäftigen wir uns im nächsten Kapitel.

Aufgaben zum Kapitel

Aufgabe 1.2: Bitfehlerquote (BER)

Aufgabe 1.2Z: Bitfehlermessung

Aufgabe 1.3: Rechteckfunktionen für Sender und Empfänger

Aufgabe 1.3Z: Schwellenwertoptimierung