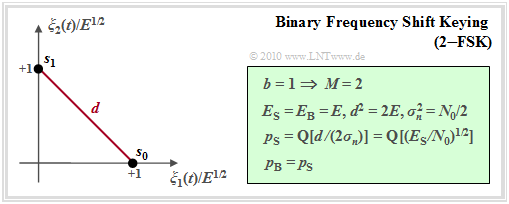Carrier Frequency Systems with Coherent Demodulation

1. Digital Signal Transmission
2. Verallgemeinerte Beschreibung digitaler Modulationsverfahren
3. Carrier Frequency Systems with Coherent Demodulation

• Previous page
• Next page

• Previous page
• Next page

Signalraumdarstellung der linearen Modulation

In den ersten drei Kapiteln dieses  vierten Hauptkapitels  „ Verallgemeinerte Beschreibung digitaler Modulationsverfahren” wurde die Struktur des optimalen Empfängers und die Signaldarstellung mittels Basisfunktionen am Beispiel der Basisbandübertragung behandelt.

Mit der gleichen Systematik und der gleichen Einheitlichkeit sollen nun auch Bandpass–Systeme betrachtet werden, die bereits in früheren Büchern bzw. Kapiteln beschrieben wurden, nämlich

• im Haupkapitel 4: „Digitale Modulationsverfahren” des Buches  Modulationsverfahren,
  

• im Kapitel  Lineare digitale Modulation – Kohärente Demodulation  des vorliegenden Buches.
  
  

Im Folgenden beschränken wir uns auf lineare Modulationsverfahren  und kohärente Demodulation. Das bedeutet, dass dem Empfänger das beim Sender zugesetzte Trägersignal hinsichtlich Frequenz und Phase exakt bekannt sein muss. Im darauf folgenden Kapitel werden  Trägerfrequenzsysteme mit nichtkohärenter Demodulation  behandelt.

Im Fall der kohärenten Demodulation kann das gesamte Übertragungssystem im  äquivalenten Tiefpassbereich  beschrieben werden und der Zusammenhang zur Basisbandübertragung ist noch offensichtlicher zu erkennen als bei Betrachtung der Bandpass–Signale.

Äquivalentes Tiefpassmodell trägermodulierter Übertragungsverfahren

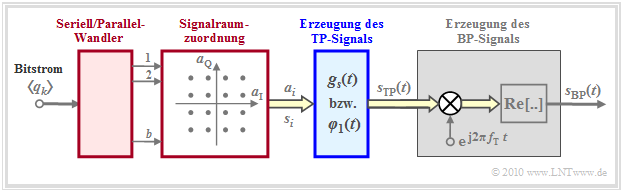
Es ergibt sich somit das skizzierte Modell. Komplexe Größen sind durch einen gelb gefüllte Doppelpfeile markiert. Zu dieser Grafik ist anzumerken:

• Aus dem ankommenden Bitstrom  $\langle q_k \rangle \in \{\rm 0, \ L \}$  werden je  $b$  Datenbits seriell/parallel gewandelt. Diese Ausgangsbits ergeben die Nachricht  $m \in \{m_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, m_{M-1} \}$, wobei  $M = 2^b$  die Stufenzahl angibt. Für das Folgende wird die Nachricht  $m = m_i$  vorausgesetzt.
  

• In der  Signalraumzuordnung  wird jeder Nachricht  $m_i$  ein komplexer Amplitudenkoeffizient  $a_i = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i}$  zugeordnet, dessen Realteil die Inphasekomponente und dessen Imaginärteil die Quadraturkomponente des späteren Sendesignals formen wird.
  

• Am Ausgang des blau markierten Blockes  Erzeugung des TP–Signals  liegt das (im allgemeinen) komplexwertige  äquivalente Tiefpass–Signal  vor, wobei  $g_s(t)$  vorerst ebenso wie  $s_{\rm TP}(t)$  auf den Bereich  $0 \le t \le T$  beschränkt sein soll. Der Index  $i$  liefert wiederum einen Hinweis auf die gesendete Nachricht  $m_i$:

$$s_{\rm TP}(t) \big {|}_{m \hspace{0.05cm}= \hspace{0.05cm} m_i} = a_i \cdot g_s(t) = a_{{\rm I}i} \cdot g_s(t) + {\rm j} \cdot a_{{\rm Q}i} \cdot g_s(t)$$

• Durch Energienormierung kommt man vom Sendegrundimpuls  $g_s(t)$  zur Basisfunktion

$$\varphi_1(t) = { g_s(t)}/{\sqrt{E_{gs}}} \hspace{0.4cm} {\rm mit} \hspace{0.4cm} E_{gs} = \int_{0}^{T} g_s(t)^2 \,{\rm d} t \hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm TP}(t) \big {|}_{m\hspace{0.05cm} =\hspace{0.05cm} m_i} = s_{{\rm I}i} \cdot \varphi_1(t) + s_{{\rm Q}i} \cdot {\rm j} \cdot \varphi_1(t) \hspace{0.05cm}.$$

• Während die Koeffizienten  $a_{{\rm I}i}$  und  $a_{{\rm Q}i}$  dimensionslos sind, weisen die neuen Koeffizienten  $s_{{\rm I}i}$  und  $s_{{\rm Q}i}$  die Einheit „Wurzel aus Energie” auf   ⇒   siehe Seite  Zur Nomenklatur im vierten Kapitel:

$$s_{{\rm I}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm I}i}\hspace{0.05cm}, \hspace{0.2cm} s_{{\rm Q}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm Q}i}\hspace{0.05cm}.$$

• Die Gleichungen zeigen, dass das hier betrachtete System im äquivalenten TP–Bereich durch je eine reelle Basisfunktion  $\varphi_1(t)$  und eine rein imaginäre Basisfunktion  $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$  oder durch eine einzige komplexe Basisfunktion  $\xi_1(t)$  vollständig beschrieben wird.
  

• Der grau hinterlegte Teil des Blockschaltbildes zeigt das Modell zur Erzeugung des Bandpass–Signals  $s_{\rm BP}(t)$, zuerst die Erzeugung des  analytischen Signals  $s_{\rm +}(t) = s_{\rm TP}(t) \cdot {\rm e}^{{\rm j}2\pi \cdot f_{\rm T} \cdot T}$  und anschließend die Realteilbildung.
  

• Die beiden Basisfunktionen des Bandpass–Signals  $s_{\rm BP}(t)$  ergeben sich hier als energienormierte und auf den Bereich  $0 \le t \le T$  zeitbegrenzte Cosinus– bzw. Minus–Sinus–Schwingungen.
  
  

Kohärente Demodulation und optimaler Empfänger

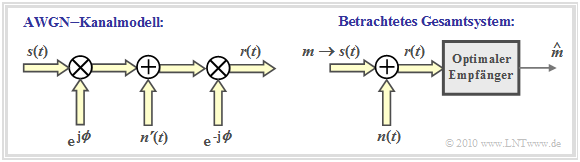
Im Folgenden gehen wir stets vom äquivalenten Tiefpass–Signal aus, wenn nicht ausdrücklich etwas anderes angegeben ist. Insbesondere sind die Signale  $s(t) = s_{\rm TP}(t)$  und  $r(t) = r_{\rm TP}(t)$  in der Grafik Tiefpass–Signale und somit im Allgemeinen komplex. Auf den Zusatz „TP” wird im Weiteren verzichtet.

AWGN–Kanalmodell für komplexe Signale

Zu dieser Abbildung ist zu anzumerken:

• Die Phasenlaufzeit des Kanals (also eine mit der Frequenz linear ansteigende Phasenfunktion) wird im Tiefpassbereich durch den zeitunabhängigen Drehfaktor  ${\rm e}^{{\rm j}\hspace{0.05cm} \phi}$  ausgedrückt.
  

• Das Signal  $n\hspace{0.05cm}'(t)$  beschreibt einen komplexen weißen Gaußschen Zufallsprozess im TP–Bereich, wie im Abschnitt  N–dimensionales Gaußsches Rauschen  angegeben. Das Hochkomma wurde angefügt, um später beim Gesamtsystem mit  $n(t)$  arbeiten zu können.
  

• Der Empfänger kennt die Kanalphase  $\phi$  und korrigiert diese durch den konjugiert–komplexen Drehfaktor  ${\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$. Damit lautet das Empfangssignal im äquivalenten Tiefpassbereich:

$$r(t) = s(t) + n\hspace{0.05cm}'(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\phi}= s(t) + n(t) \hspace{0.05cm}.$$

• Durch die Phasendrehung ändert sich an den Eigenschaften des zirkular symmetrischen Rauschens nichts   ⇒   $n(t) = n\hspace{0.05cm}'(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$ hat genau gleiche statistische Eigenschaften wie $n\hspace{0.05cm}'(t)$.
  
  

Die linke Grafik im obigen Bild verdeutlicht die soeben beschriebenen Sachverhalte.

• Die rechte Grafik zeigt das Gesamtsystem, wie es für den Rest des vierten Hauptkapitels verwendet wird.
• Nach dem AWGN–Kanal folgt ein optimaler Empfänger gemäß dem Abschnitt  N–dimensionales Gaußsches Rauschen.

$\text{Definition:}$  Ein  Symbolfehler  tritt immer dann auf, wenn  $\hat{m}$  nicht mit der gesendeten Nachricht  $m$  übereinstimmt:

$$m = m_i \hspace{0.2cm} \cap \hspace{0.2cm} \hat{m} \ne m_i \hspace{0.05cm}.$$

On–Off–Keying (2–ASK)

Das einfachste digitale Modulationsverfahren ist  On–Off–Keying  (OOK), das bereits im Buch  Modulationsverfahren  anhand seiner Bandpass–Signale ausführlich beschrieben wurde. Dort wurde dieses Verfahren teilweise auch als Amplitude Shift Keying  (2–ASK) bezeichnet.

Signalraumkonstellationen für On–Off–Keying

Dieses Verfahren kann wie folgt charakterisiert werden:

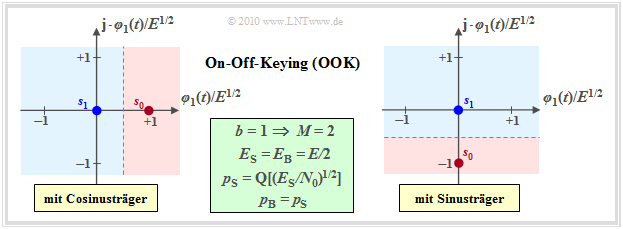
• OOK ist ein eindimensionales Modulationsverfahren  $(N = 1)$  mit  $s_{{\rm I}i} = \{0, E^{1/2}\}$  und  $s_{{\rm Q}i} \equiv 0$  bzw.  $s_{{\rm I}i} \equiv 0$  und  $s_{{\rm Q}i} = \{0, -E^{1/2}\}$. Abkürzend gilt  $E = E_{g_s}$. Die erste Kombination beschreibt ein cosinusförmiges Trägersignal, die zweite Kombination einen sinusförmigen Träger.
  

• Jedes Bit wird einem Binärsymbol zugeordnet  $(b = 1, \ M = 2)$; man benötigt also keinen Seriell/Parallel–Wandler. Bei gleichwahrscheinlichen Symbolen, was für das Folgende stets vorausgesetzt wird, ist sowohl die mittlere Energie pro Symbol  $(E_{\rm S})$  als auch die mittlere Energie pro Bit  $(E_{\rm B})$  gleich  $E/2$.
  

• Der optimale OOK–Empfänger projiziert quasi das komplexwertige Empfangssignal  $r(t)$  auf die Basisfunktion  $\varphi_1(t)$, wenn man von der linken Skizze (Cosinusträger) ausgeht.
  

• Wegen  $N = 1$  kann das Rauschen eindimensional mit der Varianz  $\sigma_n^2 = N_0/2$  angesetzt werden. Mit den Aussagen im Abschnitt  Fehlerwahrscheinlichkeit bei gleichwahrscheinlichen Binärsymbolen  erhält man für die mittlere Symbolfehlerwahrscheinlichkeit:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{\frac{E}{2 N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.$$

• Da jedes Bit genau auf ein Symbol abgebildet wird, ist die mittlere Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  genau so groß:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.$$

Binary Phase Shift Keying (BPSK)

Das sehr oft angewandte Verfahren Binary Phase Shift Keying  (BPSK), das bereits im Kapitel  Lineare digitale Modulationsverfahren  des Buches „Modulationsverfahren” anhand der Bandpass–Signale ausführlich beschrieben wurde (typisch:   Phasensprünge), unterscheidet sich von On–Off–Keying  durch eine konstante Hüllkurve.

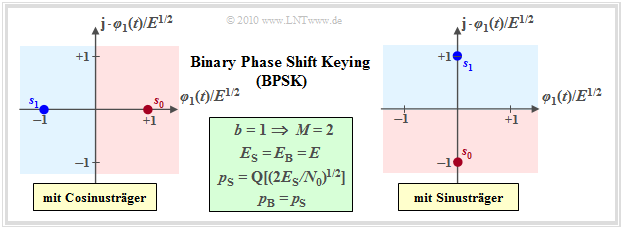
Für die Signalraumpunkte gilt stets  $\boldsymbol{s}_1 = -\boldsymbol{s}_0$. Sie lauten beispielsweise:

• $s_{{\rm I}i} = \{\pm E^{1/2}\}$ und $s_{{\rm Q}i} \equiv 0$ bei cosinusförmigem Träger,
  
• $s_{{\rm I}i} \equiv 0$ und $s_{{\rm Q}i} = \{\pm E^{1/2}\}$ bei sinusförmigem Träger.
  
  

Signalraumkonstellationen der BPSK

Anhand der in der Grafik angegebenen Gleichungen (im grün hinterlegten Feld) erkennt man die Verbesserungen gegenüber On–Off–Keying:

• Bei gegebener Normierungsenergie  $E$  ist der Abstand zwischen  $\boldsymbol{s}_0$  und  $\boldsymbol{s}_1$  doppelt so groß. Damit erhält man für die Fehlerwahrscheinlichkeit (sowohl bezogen auf Symbole wie auch auf Bits):

$$p_{\rm S} = p_{\rm B} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{2 E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.$$

• In dieser Gleichung ist ebenfalls berücksichtigt, dass nun  $E_{\rm S} = E_{\rm B} = E$  gilt, das heißt, dass nun die mittleren Energien pro Symbol bzw. pro Bit doppelt so groß sind als bei OOK.
  

• Die BPSK–Fehlerwahrscheinlichkeit ist durch den Faktor  $2$  unter der Wurzel im Argument der Q–Funktion merklich geringer als bei On–Off–Keying, wenn  $E_{\rm S}$  und  $N_0$  nicht verändert werden.
  

• Anders ausgedrückt:   BPSK benötigt bei gleichem  $N_0$  nur die halbe Symbolenergie  $E_{\rm S}$, um die gleiche Fehlerwahrscheinlichkeit wie On–Off–Keying zu erzielen. Der logarithmische Gewinn beträgt  $3 \ \rm dB$.
  

M–stufiges Amplitude Shift Keying (M–ASK)

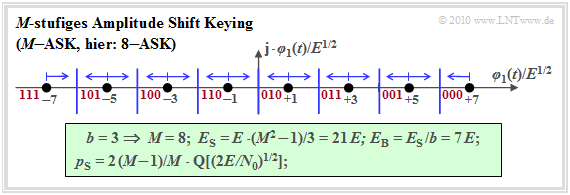
In Analogie zur  M–stufigen Basisbandübertragung  betrachten wir nun ein  $M$–stufiges Amplitude Shift Keying  ($M$–ASK), dessen Tiefpass–Signalraumkonstellation für die Parameter  $b = 3$   ⇒   $M = 8$   ⇒   $8$–ASK  wie folgt aussieht.

Signalraumkonstellation der 8-ASK

Der Name  $M$–ASK ist nicht ganz zutreffend. Vielmehr handelt es sich um ein kombiniertes ASK/PSK–Verfahren, da sich zum Beispiel die beiden innersten Signalraumpunkte  $(\pm 1)$  nicht in der Amplitude (Hüllkurve) unterscheiden, sondern nur durch die Phase  ($0^\circ$ bzw. $180^\circ$).

Weiter ist anzumerken:

• Die mittlere Energie pro Symbol  kann man für dieses eindimensionale Verfahren unter Ausnutzung der Symmetrie wie folgt berechnen:

$$E_{\rm S} = \frac{2}{M} \cdot \sum_{k = 1}^{M/2} (2k -1)^2 \cdot E = \frac{M^2 -1}{3} \cdot E \hspace{0.05cm}.$$

• Da jedes der  $M$  Symbole  $b = \log_2 (M)$  Bit darstellt, erhält man für die mittlere Energie pro Bit:

$$E_{\rm B} = \frac{E_{\rm S}}{b} = \frac{E_{\rm S}}{{\rm log_2}\, (M)} =\frac{M^2 -1}{3 \cdot {\rm log_2}\, (M)} \cdot E \hspace{0.3cm}\Rightarrow\hspace{0.3cm}M= 8\hspace{-0.1cm}: E_{\rm S}/E = 21 \hspace{0.05cm}, \hspace{0.1cm}E_{\rm B}/E = 7\hspace{0.05cm}.$$

• Die Wahrscheinlichkeit, dass eines der beiden äußeren Symbole aufgrund von AWGN–Rauschen verfälscht wird, ist somit gleich

$${\rm Pr}({\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} \text{äußeres Symbol)} = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right )\hspace{0.05cm}.$$

• Die Verfälschungswahrscheinlichkeit der  $M-2$  inneren Symbole ist doppelt so groß, da hier sowohl rechts als auch links andere Entscheidungsregionen angrenzen. Durch Mittelung erhält man für die (mittlere) Symbolfehlerwahrscheinlichkeit:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = \frac{1}{M} \cdot \left [ 2 \cdot 1 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) + (M-2) \cdot 2 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \right ]$$

$$\Rightarrow \hspace{0.3cm} p_{\rm S} = \frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) =\frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{\frac{6 \cdot E_{\rm S}}{(M^2-1) \cdot N_0}}\right ) \hspace{0.05cm}.$$

• Bei Verwendung des  Graycodes  (benachbarte Symbole unterscheiden sich jeweils um ein Bit) ist die Bitfehlerwahrscheinlichkeit  $p_{\rm B}$ näherungsweise um den Faktor  $b = \log_2 \ (M)$  kleiner als die Symbolfehlerwahrscheinlichkeit  $p_{\rm S}$:

$$p_{\rm B} \approx \frac{p_{\rm S}}{b} = \frac{2 \cdot (M-1)}{M \cdot {\rm log_2}\, (M)} \cdot {\rm Q} \left ( \sqrt{{6 \cdot {\rm log_2}\, (M)}/({M^2-1 }) \cdot { E_{\rm B}}/{ N_0}}\right ) \hspace{0.05cm}.$$

Quadraturamplitudenmodulation (M–QAM)

Signalraumkonstellation der 16-QAM

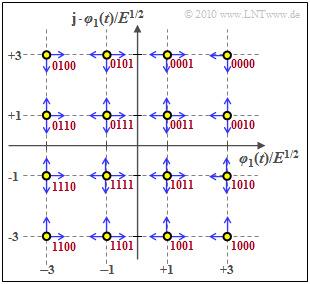
Die  Quadraturamplitudenmodulation  ($M$–QAM) ergibt sich durch je eine  $M$–ASK für Inphase– und Quadraturkomponente   ⇒   $M^2$  Signalraumpunkte.

Durch jedes Symbol werden nun  $b = \log_2 (M)$  Binärzeichen (Bit) dargestellt. Die Grafik zeigt den Sonderfall  $M = 16$   ⇒   $b = 4$. Rot eingezeichnet ist die Bitzuordnung bei  Graycodierung  (benachbarte Symbole unterscheiden sich jeweils um ein Bit).

Die mittlere Energie pro Symbol  $(E_{\rm S})$ bzw. die mittlere Energie pro pro Bit  $(E_{\rm B})$ kann man aus dem Ergebnis für die  $M$–ASK einfach ableiten (beachten Sie in der Gleichung den Unterschied zwischen einer Energie  $E$  und dem Erwartungswert  $\rm E[\text{...}]$):

$$E_{\rm S} = {\rm E} \left [ |s_{i}|^2 \right ] = {\rm E} \left [ |s_{{\rm I}i}|^2 \right ] + {\rm E} \left [ |s_{{\rm Q}i}|^2 \right ] = 2 \cdot {\rm E} \left [ |s_{{\rm I}i}|^2 \right ]$$

$$\Rightarrow \hspace{0.3cm} E_{\rm S} = 2 \cdot \frac{M_{\rm I}^2-1}{3} \cdot E = \frac{2}{3} \cdot (M-1) \cdot E\hspace{0.01cm},\hspace{0.3cm}E_{\rm B} =\frac{2 \cdot (M-1)}{3 \cdot {\rm log_2}\, (M)} \cdot E \hspace{0.01cm}.$$

Daneben zeigt die M–stufige Quadraturamplitudenmodulation folgende Eigenschaften:

• Als obere Schranke für die Symbolfehlerwahrscheinlichkeit kann die  Union Bound  herangezogen werden, wobei zu beachten ist, dass ein inneres Symbol in vier Richtungen verfälscht werden kann:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) \le \left\{ \begin{array}{c} 4 \cdot p \\ 2 \cdot p \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} M \ge 16 \hspace{0.05cm}, \\ {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} M = 4 \hspace{0.05cm},\\ \end{array} \hspace{0.4cm} {\rm mit} \hspace{0.4cm} p = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \hspace{0.05cm}.$$

• Berücksichtigt man, dass nur die  $(b-2)^2$  inneren Punkte in vier Richtungen verfälscht werden, die vier Eckpunkte dagegen nur in zwei und die restlichen in drei Richtungen (blaue Pfeile in der Grafik), so erhält man mit  $M = b^2$  die bessere Näherung

$$p_{\rm S} \approx {1}/{M} \cdot \big [(b - 2)^2 \cdot 4p + 4 \cdot 2p + 4 \cdot (b - 2) \cdot 3p \big ] = {p}/{M} \cdot \big [ 4 \cdot M - 16 \cdot \sqrt{M} + 16 + 8 + 12 \cdot \sqrt{M} - 24\big ]$$

$$\Rightarrow \hspace{0.3cm} p_{\rm S} \approx {4 \cdot p}/{M} \cdot \big [ M - \sqrt{M} \big ] = 4p \cdot \big [ 1 - {1}/{\sqrt{M}} \big ]$$

$$\Rightarrow\hspace{0.3cm} M = 16\hspace{-0.1cm}: \hspace{0.1cm} p_{\rm S} \approx 3 \cdot p = 3 \cdot {\rm Q} \big ( \sqrt{{2 E}/{N_0}}\big ) = 3 \cdot {\rm Q} \big ( \sqrt{{1/5 \cdot E_{\rm S}}/{ N_0}}\big ) \hspace{0.05cm}.$$

$\text{Fazit:}$  Bei der  $M$–QAM gilt allgemein  $E_{\rm B} = E_{\rm S}/\log_2 \hspace{0.05cm} (M)$  und bei Graycodierung zusätzlich  $p_{\rm B} = p_{\rm S}/\log_2 \hspace{0.05cm} (M)$.

Damit erhält man für die mittlere Bitfehlerwahrscheinlichkeit:

$$p_{\rm B} \approx \frac{4 \cdot (1 - 1/\sqrt{M})}{ {\rm log_2}\hspace{0.05cm} (M)} \cdot {\rm Q} \left ( \sqrt{ \frac{3 \cdot {\rm log_2}\, (M)}{M-1 } \cdot { E_{\rm B} }/{ N_0} }\right ) \hspace{0.05cm}.$$

• Die Näherung gilt für  $M \le 16$  exakt, wenn – wie für die obere Grafik vorausgesetzt – keine „diagonalen Verfälschungen” auftreten.
• Der Sonderfall „4–QAM” (ohne innere Symbole) wird in der  Aufgabe 4.13  behandelt.
  

Mehrstufiges Phase–Shift Keying (M–PSK)

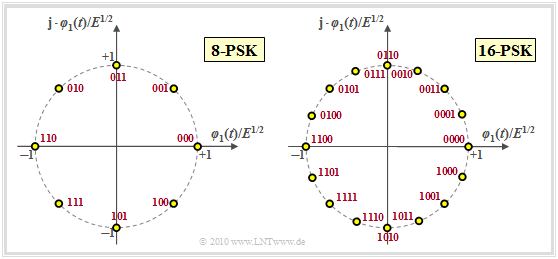
Bei mehrstufiger Phasenmodulation, wobei die Stufenzahl  $M$  in der Praxis meist eine Zweierpotenz ist, liegen alle Signalraumpunkte auf einem Kreis mit Radius  $E^{1/2}$  gleichmäßig verteilt. Damit gilt für die mittlere Symbolenergie  $E_{\rm S} = E$  und für die mittlere Energie pro Bit  $E_{\rm B} = E_{\rm S}/b = E/\hspace{-0.05cm}\log_2 \hspace{0.05cm} (M)$.

Signalraumkonstellation der 8–PSK und 16–PSK

Für die Inphase– und die Quadraturkomponente der Signalraumpunkte  $\boldsymbol{s}_i$  gilt allgemein  $(i = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, \hspace{0.05cm}M-1)$:

$$s_{{\rm I}i} = \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},\hspace{0.2cm} s_{{\rm Q}i} = \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} || \boldsymbol{ s}_i || = \sqrt{ s_{{\rm I}i}^2 + s_{{\rm Q}i}^2} = 1 \hspace{0.05cm}.$$

Der Phasenoffset ist in obiger Grafik jeweils zu  $\phi_{\rm off} = 0$  gesetzt. Die 4–PSK mit  $\phi_{\rm off} = \pi/4 \ (45^\circ)$  ist identisch mit der  4–QAM. Der Abstand zwischen zwei benachbarten Punkten ist in allen Fällen gleich:

$$d_{\rm min} = d_{\rm 0, \hspace{0.05cm}1} = d_{\rm 1, \hspace{0.05cm}2} = \hspace{0.05cm}\text{...} \hspace{0.05cm} = d_{M-1, \hspace{0.05cm}0} = 2 \cdot \sqrt{E} \cdot \sin (\pi/M)$$

$$\Rightarrow\hspace{0.3cm} M = 4\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} = \sqrt{2} \approx 1.414 \hspace{0.05cm}, \hspace{0.8cm} M = 8\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.765 \hspace{0.05cm},\hspace{0.8cm} M = 16\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.390 \hspace{0.05cm}.$$

Die obere Schranke  $p_{\rm UB}$  für die AWGN–Symbolfehlerwahrscheinlichkeit nach der  Union Bound  liefert:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) \le 2 \cdot {\rm Q} \left ( \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right ) = p_{\rm UB} \hspace{0.05cm}.$$

Man erkennt:

• Für  $M = 2$  (BPSK) erhält man daraus die Abschätzung  $p_{\rm S} \le p_{\rm UB} =2 \cdot {\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$. Ein Vergleich mit der auf der  BPSK–Seite  angegebenen Gleichung  $p_{\rm S} ={\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$  zeigt, dass in diesem Sonderfall die „Union Bound” als obere Schranke den doppelten Wert liefert.
• Je größer  $M$  ist, umso genauer nähert  $p_{\rm UB}$  die exakte Symbolfehlerwahrscheinlichkeit  $p_{\rm S}$  an. Das interaktive Applet  Mehrstufige PSK & Union Bound  gibt auch die genauere, durch Simulation gewonnene Fehlerwahrscheinlichkeit an.
  

$\text{Fazit:}$  Die Schranke für die M–PSK–Bitfehlerwahrscheinlichkeit lautet (Graycode  ⇒  rote Beschriftung vorausgesetzt):

$$p_{\rm B} \le \frac{2}{ {\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{ {\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.$$

• Diese Schranke muss man allerdings nur für  $M > 4$  anwenden.
• Für  $M = 2$  (BPSK) und  $M = 4$  (Identität zwischen 4–PSK und 4–QAM) kann man die Bitfehlerwahrscheinlichkeit exakt angeben:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.$$

Binary Frequency Shift Keying (2–FSK)

Auch diese Modulationsart mit Parameter  $b = 1$   ⇒   $M = 2$  wurde bereits im Abschnitt  FSK – Frequency Shift Keying  des Buches „Modulationsverfahren” anhand der Bandpass–Signale ausführlich beschrieben.

Die beiden möglichen Signalformen werden im Bereich  $0 \le t \le T$  durch zwei unterschiedliche Frequenzen dargestellt:

$$s_{\rm BP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} + \Delta f_{\rm A})\cdot t)\hspace{0.05cm},$$

$$s_{\rm BP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} - \Delta f_{\rm A})\cdot t)\hspace{0.05cm}.$$

$f_{\rm T}$  bezeichnet die Trägerfrequenz und  $\Delta f_{\rm A}$  den (einseitigen) Frequenzhub. Die mittlere Energie pro Symbol bzw. pro Bit ist jeweils gleich:

$$E_{\rm S} = E_{\rm B} = E = \frac{A^2 \cdot T}{2} \hspace{0.05cm}.$$

Hier soll nun die FSK im äquivalenten Tiefpass–Signalraum betrachtet werden. Dann gilt:

$$s_{\rm TP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

$$s_{\rm TP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

und für das innere Produkt erhält man

$$< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \hspace{-0.1cm} \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t = A^2 \cdot \int_{0}^{T} {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t} \,{\rm d} t = \frac{A^2}{{\rm j} \cdot 4\pi \cdot \Delta f_{\rm A}} \cdot \big [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot T} - 1 \big ] \hspace{0.05cm}.$$

$\text{Definition:}$  Der  Modulationsindex  $h = 2 \cdot \Delta f_{\rm A}\hspace{0.03cm}\cdot T$  ist das Verhältnis zwischen dem gesamten (beideseitigen) Frequenzhub  $(2 \cdot \Delta f_{\rm A})$  und der Symbolrate  $(1/T)$.

Die beiden Signale sind dann orthogonal, wenn dieses innere Produkt gleich Null ist:

$$< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \frac{A^2\cdot T}{{\rm j} \cdot 2\pi \cdot h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2h} - 1 \right ] = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T = 1,\hspace{0.1cm} 2, \hspace{0.1cm}3,\ \text{ ... }\hspace{0.05cm}.$$

Signalraumkonstellation der FSK, falls  $h$  ganzzahlig

Setzt man den Modulationsindex  $h$  als ganzzahlig voraus, so lassen sich die Tiefpass–Signale in der Form

$$s_{\rm TP0}(t) = \sqrt{E} \cdot \xi_1(t) \hspace{0.05cm},$$

$$s_{\rm TP1}(t) = \sqrt{E} \cdot \xi_2(t)$$

mit komplexen Basisfunktionen darstellen:

$$\xi_1(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

$$\xi_2(t)= \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.$$

Es ergibt sich die hier skizzierte Signalraumdarstellung der binären FSK.

$\text{Fazit:}$ 

• Bei ganzzahligem Modulationsindex  $h$  sind die Tiefpass-Signale  $s_{\rm TP0}(t)$  und  $s_{\rm TP1}(t)$  der binären FSK zueinander orthogonal.
  

• Damit ergibt sich für die Symbolfehlerwahrscheinlichkeit (Herleitung in der Grafik):

$$p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q} \left ( \sqrt{ { {E_{\rm S} } }/{ N_0} }\right ) \hspace{0.05cm}.$$

• Die Bitfehlerwahrscheinlichkeit hat den gleichen Wert:   $p_{\rm B} = p_{\rm S}$.

Hinweis: Im Gegensatz zur Darstellung in [KöZ08] ist hier der Frequenzhub  $\Delta f_{\rm A}$  einseitig definiert. Deshalb unterscheiden sich die Gleichungen teilweise um den Faktor  $2$. Arbeitet man jedoch mit dem Modulationsindex  $h$, so gibt es keine Unterschiede.

Minimum Shift Keying (MSK)

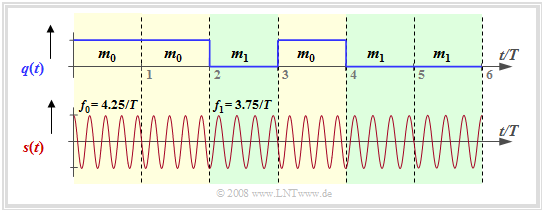
Unter  Minimum Shift Keying  (MSK) versteht man ein binäres FSK–System mit dem Modulationsindex  $h = 0.5$   ⇒   Frequenzhub $\Delta f_{\rm A} = 1/(2T)$. Die Grafik zeigt ein MSK–Signal für die Trägerfrequenz  $f_{\rm T} = 4/T$:

• Die beiden Frequenzen innerhalb des Sendsignals sind  $f_{\rm 0} = f_{\rm T} + 1/(4T)$  zur Darstellung der Nachricht  $m_0$  (gelbe Hinterlegung) sowie  $f_{\rm 1} = f_{\rm T} -1/(4T)$   ⇒   Nachricht  $m_1$  (grüne Hinterlegung).
• In der Grafik ist auch eine kontinuierliche Phasenanpassung bei den Übergängen berücksichtigt, um die Signalbandbreite weiter zu verringern. Man spricht dann von  Continuous Phase Modulation  (CPM).
  

Quellensignal und Bandpass–MSK–Signal

Ohne diese Phasenanpassung lauten die beiden Bandpass–Signalformen:

$$s_{\rm BP0}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

$$s_{\rm BP1}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm}.$$

Bildet man das innere Produkt der Bandpass–Signale, so erhält man mit  $f_{\rm \Delta} = f_0 - f_1$  und  $f_{\rm \Sigma} = f_0 + f_1$:

$$< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {2E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_0 t) \cdot \cos( 2\pi f_1 t)\,{\rm d} t = {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Delta} t) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Sigma} t) \,{\rm d} t$$

$$\Rightarrow \hspace{0.3cm}< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm} \cos( \pi \cdot {t}/{T}) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm}\cos( 2\pi \cdot 2 f_{\rm T} \cdot t) \,{\rm d} t \hspace{0.05cm}.$$

Das erste Integral ist Null $($Integral über „Cosinus” von  $0$  bis  $\pi)$. Für  $f_{\rm T} \gg 1/T$, was man in der Praxis voraussetzen kann, verschwindet auch das zweite Integral. Damit erhält man für das innere Produkt:  

$$< \hspace{0.02cm} s_{\rm BP0}(t) \cdot s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm}= 0 \hspace{0.05cm}.$$

$\text{Fazit:}$ 

• Damit ist gezeigt, dass für den Modulationsindex  $h = 0.5$  (also  MSK) und allen Vielfachen hiervon die beiden Bandpass–Signale orthogonal sind.
• Mit den neuen reellen Basisfunktionen

$$\varphi_1(t) = \sqrt{2/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

$$\varphi_2(t) = \sqrt{2/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T$$

erhält man die genau gleiche Signalraumkonstellation wie für geradzahliges  $h = 1, 2, 3, \ \text{ ...}$.

• Es ergibt sich somit auch die gleiche Fehlerwahrscheinlichkeit:

$$p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q} \left ( \sqrt{ { {E_{\rm S} } }/{ N_0} }\right ) = p_{\rm B} \hspace{0.05cm}.$$

Aufgaben zum Kapitel

Aufgabe 4.11: On-Off-Keying und Binary Phase Shift Keying

Aufgabe 4.11Z: Nochmals OOK und BPSK

Aufgabe 4.12: Berechnungen zur 16-QAM

Aufgabe 4.13: Vierstufige QAM

Aufgabe 4.14: 8-PSK und 16-PSK

Aufgabe 4.14Z: 4-QAM und 4-PSK

Aufgabe 4.15: Optimale Signalraumbelegung

Aufgabe 4.16: Binary Frequency Shift Keying