Different Entropy Measures of Two-Dimensional Random Variables

Definition of entropy using supp(P_XY)

We briefly summarise the results of the last chapter again, assuming the two-dimensional random variable $XY$ with the probability function $P_{XY}(X,\ Y)$ . At the same time we use the notation

$${\rm supp} (P_{XY}) = \big \{ \hspace{0.05cm}(x,\ y) \in XY \hspace{0.05cm}, \hspace{0.3cm} {\rm where} \hspace{0.15cm} P_{XY}(X,\ Y) \ne 0 \hspace{0.05cm} \big \} \hspace{0.05cm};$$

$\text{Summarising the last chapter:}$

With this subset $\text{supp}(P_{XY}) ⊂ P_{XY}$ , the following holds for

the joint entropy :

$$H(XY) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.05cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(x, y)} \hspace{0.05cm}.$$

the entropies of the 1D random variables $X$ and $Y$:

$$H(X) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\right ] =\hspace{-0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{X})} \hspace{-0.2cm} P_{X}(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(x)} \hspace{0.05cm},$$

$$H(Y) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(Y)}\right ] =\hspace{-0.2cm} \sum_{y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Y})} \hspace{-0.2cm} P_{Y}(y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(y)} \hspace{0.05cm}.$$

$\text{Example 1:}$ We refer again to the examples on the joint probability and joint entropy in the last chapter. For the 2D probability function $P_{RB}(R, B)$ in $\text{example 5}$ there with the parameters

$R$ ⇒ numbers of the red die and
$B$ ⇒ number of the blue die

the sets $P_{RB}$ and $\text{supp}(P_{RB})$ are identical. Here, all $6^2 = 36$ squares are occupied by non-zero values.

For the 2D probability function $P_{RS}(R, S)$ in $\text{example 6}$ mit den Parametern

$R$ ⇒ numbers of the red die
$S = R + B$ ⇒ sum of both dice

there are $6 · 11 = 66$ squares, many of which, however, are empty, i.e. stand for the probability „0” .

The subset $\text{supp}(P_{RS})$ , on the other hand, contains only the $36$ shaded squares with non-zero probabilities.
The entropy remains the same no matter whether one averages over all elements of $P_{RS}$ or only over the elements of $\text{supp}(P_{RS})$ since for $x → 0$ the limit is $x · \log_2 ({1}/{x}) = 0$ ist.

Conditional probability and conditional entropy

In the book „Theory of Stochastic Signals” the following conditional probabilities were given for the case of two events $X$ and $Y$ ⇒ Bayes' theorem:

$${\rm Pr} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (Y)} \hspace{0.05cm}, \hspace{0.5cm} {\rm Pr} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (X)} \hspace{0.05cm}.$$

Applied to probability functions, one thus obtains:

$$P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{P_{XY}(X, Y)}{P_{Y}(Y)} \hspace{0.05cm}, \hspace{0.5cm} P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{P_{XY}(X, Y)}{P_{X}(X)} \hspace{0.05cm}.$$

Analogous to the joint entropy $H(XY)$ , the following entropy functions can be derived here:

$\text{Definitions:}$

The conditional entropy of the random variable $X$ under condition $Y$ is:

$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ] = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{Y}(y)}{P_{XY}(x, y)} \hspace{0.05cm}.$$

Similarly, for the second conditional entropy we obtain:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.05cm} X) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}Y\hspace{0.03cm} \mid \hspace{0.01cm} X} (Y \hspace{-0.08cm}\mid \hspace{-0.05cm}X)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y\hspace{-0.03cm} \mid \hspace{-0.01cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{X}(x)}{P_{XY}(x, y)} \hspace{0.05cm}.$$

In the argument of the logarithm function there is always a conditional probability function ⇒ $P_{X\hspace{0.03cm}| \hspace{0.03cm}Y}(·)$ bzw. $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(·)$, while the joint probability ⇒ $P_{XY}(·)$ is needed for the expectation value formation.

For the conditional entropies, there are the following limitations:

Both $H(X|Y)$ and $H(Y|X)$ are always greater than or equal to zero. From $H(X|Y) = 0$ it follows directly also $H(Y|X) = 0$. Both are only possible for disoint sets $X$ and $Y$ .
$H(X|Y) ≤ H(X)$ and $H(Y|X) ≤ H(Y)$ always apply. These statements are plausible if one realises that one can also use „uncertainty” synonymously for „entropy” . For: the uncertainty with respect to the quantity $X$ cannot be increased by knowing $Y$ .
Except in the case of statistical independence ⇒ $H(X|Y) = H(X)$ , $H(X|Y) < H(X)$ always holds. Because of $H(X) ≤ H(XY)$ and $H(Y) ≤ H(XY)$ , $H(X|Y) ≤ H(XY)$ and $H(Y|X) ≤ H(XY)$ therefore also hold. Thus, a conditional entropy can never become larger than the joint entropy.

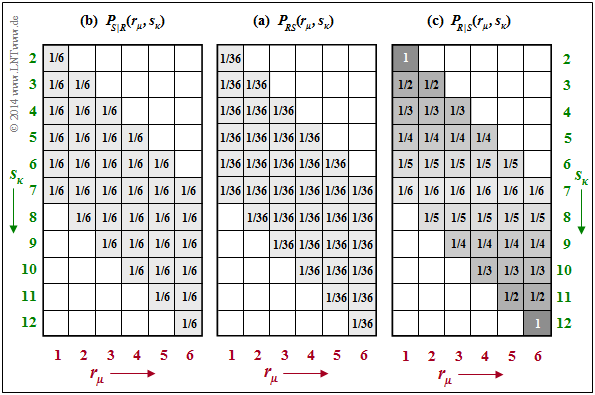
$\text{Example 2:}$ We consider the joint probabilities $P_{RS}(·)$ of our dice experiment, which were determined in the last chapter als $\text{example 6}$ . $P_{RS}(·)$ is given again in the middle of the following graph.

Joint probabilities $P_{RS}$ and conditional probabilities $P_{S \vert R}$ and $P_{R \vert S}$

The two conditional probability functions are drawn on the outside:

Given on the left is the conditional probability function $P_{S \vert R}(⋅) = P_{SR}(⋅)/P_R(⋅)$. Because of $P_R(R) = \big [1/6, \ 1/6, \ 1/6, \ 1/6, \ 1/6, \ 1/6 \big ]$ the same probability value $1/6$ is here in all shaded fields ⇒ $\text{supp}(P_{S\vert R}) = \text{supp}(P_{R\vert S})$ . From this follows for the conditional entropy:

$$H(S \hspace{-0.1cm}\mid \hspace{-0.13cm} R) = \hspace{-0.2cm} \sum_{(r, s) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{RS})} \hspace{-0.6cm} P_{RS}(r, s) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}S \hspace{0.03cm} \mid \hspace{0.03cm} R} (s \hspace{-0.05cm}\mid \hspace{-0.05cm} r)} = 36 \cdot \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bits} \hspace{0.05cm}.$$

On the right, the conditional probability function $P_{R\vert S}(⋅) = P_{RS}(⋅)/P_S(⋅)$ is given with $P_S(⋅)$ according to $\text{example 6}$ . The same non-zero fields result ⇒ $\text{supp}(P_{R\vert S}) = \text{supp}(P_{S\vert R})$. However, the probability values now increase continuously from the centre $(1/6)$ towards the edges up to probability $1$ in the corners. It follows that:

$$H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} S) = \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) + \frac{2}{36} \cdot \sum_{i=1}^5 \big [ i \cdot {\rm log}_2 \hspace{0.1cm} (i) \big ]= 1.896\ {\rm bit} \hspace{0.05cm}.$$

On the other hand, for the conditional probabilities of the 2D random variable $RB$ according to $\text{example 5}$ , one obtains because of $P_{RB}(⋅) = P_R(⋅) · P_B(⋅)$:

$$\begin{align*}H(B \hspace{-0.1cm}\mid \hspace{-0.13cm} R) \hspace{-0.15cm} & = \hspace{-0.15cm} H(B) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm},\\ H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} B) \hspace{-0.15cm} & = \hspace{-0.15cm} H(R) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm}.\end{align*}$$

Transinformation zwischen zwei Zufallsgrößen

Wir betrachten die Zufallsgröße $XY$ mit der 2D–Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$. Bekannt seien auch die 1D–Funktionen $P_X(X)$ und $P_Y(Y)$.

Nun stellen sich folgende Fragen:

Wie vermindert die Kenntnis der Zufallsgröße $Y$ die Unsicherheit bezüglich $X$?
Wie vermindert die Kenntnis der Zufallsgröße $X$ die Unsicherheit bezüglich $Y$?

Zur Beantwortung benötigen wir eine für die Informationstheorie substantielle Definition:

$\text{Definition:}$ Die Transinformation (englisch: Mutual Information) zwischen den Zufallsgrößen $X$ und $Y$ – beide über dem gleichen Alphabet – ist wie folgt gegeben:

$$I(X;\ Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] =\hspace{-0.25cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(x, y)} {P_{X}(x) \cdot P_{Y}(y) } \hspace{0.01cm}.$$

Ein Vergleich mit dem letzten Kapitel zeigt, dass die Transinformation auch als Kullback–Leibler–Distanz zwischen der 2D–PMF $P_{XY}$ und dem Produkt $P_X · P_Y$ geschrieben werden kann:

$$I(X;Y) = D(P_{XY} \hspace{0.05cm}\vert \vert \hspace{0.05cm} P_X \cdot P_Y) \hspace{0.05cm}.$$

Es ist somit offensichtlich, dass stets $I(X;\ Y) ≥ 0$ gilt. Wegen der Symmetrie ist auch $I(Y;\ X)$ = $I(X;\ Y)$.

Sucht man in einem Wörterbuch die Übersetzung für „mutual”, so findet man unter Anderem die Begriffe „gemeinsam”, „gegenseitig”, „beidseitig” und „wechselseitig”. Und ebenso sind in Fachbüchern für $I(X; Y)$ auch die Bezeichnungen gemeinsame Entropie und gegenseitige Entropie üblich. Wir sprechen aber im Folgenden durchgängig von der Transinformation $I(X; Y)$ und versuchen nun eine Interpretation dieser Größe:

Durch Aufspalten des $\log_2$–Arguments entsprechend

$$I(X;Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac{1} {P_{X}(X) }\right ] - {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac {P_{Y}(Y) }{P_{XY}(X, Y)} \right ] $$

erhält man unter Verwendung von $P_{X|Y}(\cdot) = P_{XY}(\cdot)/P_Y(Y)$:

$$I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) \hspace{0.05cm}.$$

Das heißt: Die Unsicherheit hinsichtlich der Zufallsgröße $X$ ⇒ Entropie $H(X)$ vermindert sich bei Kenntnis von $Y$ um den Betrag $H(X|Y)$. Der Rest ist die Transinformation $I(X; Y)$.
Bei anderer Aufspaltung kommt man zum Ergebnis

$$I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$$

Ergo: Die Transinformation $I(X; Y)$ ist symmetrisch ⇒ $X$ sagt genau so viel über $Y$ aus wie $Y$ über $X$ ⇒ gegenseitige Information. Das Semikolon weist auf die Gleichberechtigung hin.

$\text{Fazit:}$ Oft werden die hier genannten Gleichungen durch ein Schaubild verdeutlicht, so auch in den folgenden Beispielen. Daraus erkennt man, dass auch folgende Gleichungen zutreffen:

$$I(X;\ Y) = H(X) + H(Y) - H(XY) \hspace{0.05cm},$$

$$I(X;\ Y) = H(XY) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$$

$\text{Beispiel 3:}$ Wir kommen (letztmalig) auf das Würfel–Experiment mit dem roten $(R)$ und dem blauen $(B)$ Würfel zurück. Die Zufallsgröße $S$ gibt die Summe der beiden Würfel an: $S = R + B$. Wir betrachten hier die 2D–Zufallsgröße $RS$. In früheren Beispielen haben wir berechnet:

die Entropien $H(R) = 2.585 \ \rm bit$ und $H(S) = 3.274 \ \rm bit$ ⇒ Beispiel 6 im letzten Kapitel,
die Verbundentropie $H(RS) = 5.170 \ \rm bit$ ⇒ Beispiel 6 im letzten Kapitel,
die bedingten Entropien $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R) = 2.585 \ \rm bit$ und $H(R \hspace{0.05cm} \vert \hspace{0.05cm} S) = 1.896 \ \rm bit$ ⇒ Beispiel 2 im vorherigen Abschnitt.

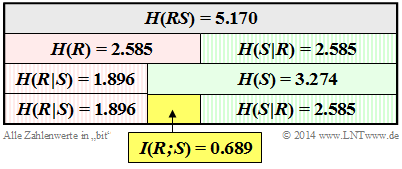
Schaubild aller Entropien des „Würfelexperiments”

Diese Größen sind in der Grafik zusammengestellt, wobei die Zufallsgröße $R$ durch die Grundfarbe „Rot” und die Summe $S$ durch die Grundfarbe „Grün” markiert sind. Bedingte Entropien sind schraffiert. Man erkennt aus dieser Darstellung:

Die Entropie $H(R) = \log_2 (6) = 2.585\ \rm bit$ ist genau halb so groß wie die Verbundentropie $H(RS)$. Denn: Kennt man $R$, so liefert $S$ genau die gleiche Information wie die Zufallsgröße $B$, nämlich $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R) = H(B) = \log_2 (6) = 2.585\ \rm bit$. Hinweis: $H(R)$ = $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ gilt allerdings nur in diesem Beispiel, nicht allgemein.
Die Entropie $H(S) = 3.274 \ \rm bit$ ist im vorliegenden Beispiel erwartungsgemäß größer als $H(R)= 2.585\ \rm bit$. Wegen $H(S) + H(R \hspace{0.05cm} \vert \hspace{0.05cm} S) = H(R) + H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ muss deshalb $H(R \hspace{0.05cm} \vert \hspace{0.05cm} S)$ gegenüber $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ um den gleichen Betrag $I(R;\ S) = 0.689 \ \rm bit$ kleiner sein als $H(R)$ gegenüber $H(S)$.
Die Transinformation (englisch: Mutual Information) zwischen den Zufallsgrößen $R$ und $S$ ergibt sich aber auch aus der Gleichung

$$I(R;\ S) = H(R) + H(S) - H(RS) = 2.585\ {\rm bit} + 3.274\ {\rm bit} - 5.170\ {\rm bit} = 0.689\ {\rm bit} \hspace{0.05cm}. $$

Bedingte Transinformation

Wir betrachten nun drei Zufallsgrößen $X$, $Y$ und $Z$, die zueinander in Beziehung stehen (können).

$\text{Definition:}$ Die bedingte Transinformation (englisch: Conditional Mutual Information) zwischen den Zufallsgrößen $X$ und $Y$ bei gegebenem $Z = z$ lautet:

$$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z = z) - H(X\vert\hspace{0.05cm}Y ,\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$

Man bezeichnet als die bedingte Transinformation zwischen den Zufallsgrößen $X$ und $Y$ für die Zufallsgröße $Z$ allgemein nach Mittelung über alle $z \in Z$:

$$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z ) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z ) - H(X\vert\hspace{0.05cm}Y Z )= \hspace{-0.3cm} \sum_{z \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Z})} \hspace{-0.25cm} P_{Z}(z) \cdot I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$

$P_Z(Z)$ ist die Wahrscheinlichkeitsfunktion (PMF) der Zufallsgröße $Z$ und $P_Z(z)$ die Wahrscheinlichkeit für die Realisierung $Z = z$.

$\text{Bitte beachten Sie:}$

Für die bedingte Entropie gilt bekanntlich die Größenrelation $H(X\hspace{0.05cm}\vert\hspace{0.05cm}Z) ≤ H(X)$.
Für die Transinformation gilt diese Größenrelation nicht unbedingt:
$I(X; Y\hspace{0.05cm}\vert\hspace{0.05cm}Z)$ kann kleiner, gleich, aber auch größer sein als $I(X; Y)$.

2D–PMF $P_{XZ}$

$\text{Beispiel 4:}$ Wir betrachten die binären Zufallsgrößen $X$, $Y$ und $Z$ mit folgenden Eigenschaften:

$X$ und $Y$ seien statistisch unabhängig. Für ihre Wahrscheinlichkeitsfunktionen gelte:

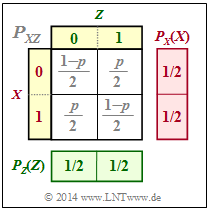
$$P_X(X) = \big [1/2, \ 1/2 \big], \hspace{0.2cm} P_Y(Y) = \big[1– p, \ p \big] \ ⇒ \ H(X) = 1\ {\rm bit}, \hspace{0.2cm} H(Y) = H_{\rm bin}(p).$$

$Z$ ist die Modulo–2–Summe von $X$ und $Y$: $Z = X ⊕ Y$.

Aus der Verbund–Wahrscheinlichkeitsfunktion $P_{XZ}$ gemäß der oberen Grafik folgt:

Durch Summation der Spalten–Wahrscheinlichkeiten ergibt sich $P_Z(Z) = \big [1/2, \ 1/2 \big ]$ ⇒ $H(Z) = 1\ {\rm bit}$.
$X$ und $Z$ sind ebenfalls statistisch unabhängig, da für die 2D–PMF $P_{XZ}(X, Z) = P_X(X) · P_Z(Z)$ gilt.
Daraus folgt: $H(Z\hspace{0.05cm}\vert\hspace{0.05cm} X) = H(Z)$ und $H(X \hspace{0.05cm}\vert\hspace{0.05cm} Z) = H(X)$ sowie $I(X; Z) = 0$.

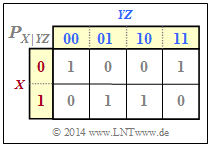
Bedingte 2D–PMF $P_{X\hspace{0.05cm}\vert\hspace{0.05cm}YZ}$

Aus der bedingten Wahrscheinlichkeitsfunktion $P_{X\vert YZ}$ gemäß der unteren Grafik lassen sich berechnen:

$H(X\hspace{0.05cm}\vert\hspace{0.05cm} YZ) = 0$, da alle $P_{X\hspace{0.05cm}\vert\hspace{0.05cm} YZ}$–Einträge entweder $0$ oder $1$ sind ⇒ bedingte Entropie,
$I(X; YZ) = H(X) - H(X\hspace{0.05cm}\vert\hspace{0.05cm} YZ) = H(X)= 1 \ {\rm bit}$ ⇒ Transinformation,
$I(X; Y\vert Z) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z) =H(X)=1 \ {\rm bit} $ ⇒ bedingte Transinformation.

Im vorliegenden Beispiel ist also

die bedingte Transinformation $I(X; Y\hspace{0.05cm}\vert\hspace{0.05cm} Z) = 1$
größer als die herkömmliche Transinformation $I(X; Y) = 0$.

Kettenregel der Transinformation

Bisher haben wir die Transinformation nur zwischen zwei eindimensionalen Zufallsgrößen betrachtet. Nun erweitern wir die Definition auf insgesamt $n + 1$ Zufallsgrößen, die wir aus Darstellungsgründen mit $X_1$, ... , $X_n$ sowie $Z$ bezeichnen. Dann gilt:

$\text{Kettenregel der Transinformation:}$

Die Transinformation zwischen der $n$–dimensionalen Zufallsgröße $X_1 X_2 \hspace{0.05cm}\text{...} \hspace{0.05cm} X_n$ und der Zufallsgröße $Z$ lässt sich wie folgt darstellen und berechnen:

$$I(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n;Z) = I(X_1;Z) + I(X_2;Z \vert X_1) + \hspace{0.05cm}\text{...} \hspace{0.1cm}+ I(X_n;Z\vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{n-1}) = \sum_{i = 1}^{n} I(X_i;Z \vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \hspace{0.05cm}.$$

$\text{Beweis:}$ Wir beschränken uns hier auf den Fall $n = 2$, also auf insgesamt drei Zufallsgrößen, und ersetzen $X_1$ durch $X$ und $X_2$ durch $Y$. Dann erhalten wir:

$$\begin{align*}I(X\hspace{0.05cm}Y;Z) & = H(XY) - H(XY\hspace{0.05cm} \vert \hspace{0.05cm}Z) = \\ & = \big [ H(X)+ H(Y\hspace{0.05cm} \vert \hspace{0.05cm} X)\big ] - \big [ H(X\hspace{0.05cm} \vert \hspace{0.05cm} Z) + H(Y\hspace{0.05cm} \vert \hspace{0.05cm} XZ)\big ] =\\ & = \big [ H(X)- H(X\hspace{0.05cm} \vert \hspace{0.05cm} Z)\big ] - \big [ H(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) + H(Y\hspace{0.05cm} \vert \hspace{0.05cm}XZ)\big ]=\\ & = I(X;Z) + I(Y;Z \hspace{0.05cm} \vert \hspace{0.05cm} X) \hspace{0.05cm}.\end{align*}$$

Aus dieser Gleichung erkennt man, dass die die Größenrelation $I(X Y; Z) ≥ I(X; Z)$ immer gegeben ist.

Gleichheit ergibt sich für die bedingte Transinformation $I(Y; Z \hspace{0.05cm} \vert \hspace{0.05cm} X) = 0$,
also dann, wenn die Zufallsgrößen $Y$ und $Z$ für ein gegebenes $X$ statistisch unabhängig sind.

$\text{Beispiel 5:}$ Wir betrachten die Markovkette $X → Y → Z$. Für eine solche Konstellation gilt stets das Data Processing Theorem mit der folgenden Konsequenz, die sich aus der Kettenregel der Transinformation ableiten lässt:

$$I(X;Z) \hspace{-0.05cm} \le \hspace{-0.05cm}I(X;Y ) \hspace{0.05cm},$$

$$I(X;Z) \hspace{-0.05cm} \le \hspace{-0.05cm} I(Y;Z ) \hspace{0.05cm}.$$

Das Theorem besagt somit:

Man kann durch Manipulation $($Processing $Z)$ der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
Die Datenverarbeitung $Y → Z$ $($durch einen zweiten Prozessor$)$ dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen.

Weitere Informationen zum Data Processing Theorem finden Sie in der Aufgabe 3.15.