Conclusions from the Allocation Theorem

1. Linear and Time Invariant Systems
2. Beschreibung kausaler realisierbarer Systeme
3. Conclusions from the Allocation Theorem

• Previous page
• Next page

• Previous page
• Next page

# OVERVIEW OF THE THIRD MAIN CHAPTER #

In the first two chapters, filter functions with real-valued frequency responses were mostly considered for reasons of presentation so that the associated time function is symmetric about zero-time. However, the impulse response of a realisable system must always be causal, that is,  $h(t)$  must be identical to zero for  $t < 0$ . This strong asymmetry of the time function  $h(t)$,  though, implies at the same time that the frequency response  $H(f)$  of a realisable system is always complex-valued with the exception of  $H(f) = K$  where there is a fixed relation between its real part and imaginary part.

This third chapter provides a recapitulatory account of the description of causal realizable systems, which differ also in the mathematical methods from those commonly used with non-causal systems.

In detail, the following is dealt with:

• the Hilbert transformation, which states how real and imaginary parts of  $H(f)$  are related,
• the Laplace transformation, which yields another spectral function  $H_{\rm L}(p)$  for causal  $h(t)$ ,
• the description of realizable systems by the pole-zero plot, as well as
• the inverse Laplace transformation using the theory of functions (residue theorem).

For this chapter we recommend

• the educational video  Arithmetic with complex numbers for preparation, as well as
• the interactive applet  Causal systems – Laplace transformation - a coherent depiction.

Prerequisites for the entire "realizable systems" chapter

In the first two chapters, mostly real  transfer functions   $H(f)$  were considered for which the associated impulse response  $h(t)$  is consequently always symmetric with respect to the reference time  $t = 0$ . Such transfer functions

• are suitable to explain basic relationships in a simple way,
• but unfortunately are not realizable for reasons of causality.

This becomes clear if the definition of the impulse response is considered:

$\text{Definition:}$  The  impulse response  $h(t)$  is equal to the output signal  $y(t)$  of the system if an infinitely short impulse with an infinitely large amplitude is applied to the input at time  $t = 0$ :   $x(t) = δ(t)$. Such an impulse is called a Dirac impulse.

It is obvious that no impulse response can be realized for which  $h(t < 0) ≠ 0$  holds.

$\text{Definition:}$  For a  causal system  the impulse response $h(t)$ is identical to zero for all times  $t < 0$ .

The only real transfer function that satisfies the causality condition "the output signal cannot start before the input signal" is:

$$H(f) = K \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h(t) = K \cdot \delta(t).$$

All other real-valued transfer functions  $H(f)$  describe non-causal systems and thus cannot be realized by an (electrical) circuit network.

$\text{In other words:}$   Except for the transfer function  $H(f) = K,$  any realistic transfer function is complex.

• If   $K=1$ holds additionally, the transfer function is said to be ideal. 
• The output  $y(t)$  is then identical to the input  $x(t)$  – even without attenuation or amplification.

Real and imaginary part of a causal transfer function

Any causal impulse response  $h(t)$  can be represented as the sum of an even part  $h_{\rm g}(t)$  and an odd part  $h_{\rm u}(t)$ :

$$\begin{align*} h_{ {\rm g}}(t) & = {1}/{2}\cdot \big[ h(t) + h(-t) \big]\hspace{0.05cm},\\ h_{ {\rm u}}(t) & = {1}/{2}\cdot \big[ h(t) - h(-t) \big] = h_{ {\rm g}}(t) \cdot {\rm sign}(t)\hspace{0.05cm} .\end{align*}$$

Here, the so-called  sign function  is used:

$${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ +1 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} { t < 0,} \\ { t > 0.} \\ \end{array}$$

$\text{Example 1:}$  The graph shows this splitting for a causal exponentially decreasing impulse response of a low-pass filter of first-order corresponding to  Exercise 1.3Z:

$$h(t) = \left\{ \begin{array}{c} 0 \\ 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \begin{array}{c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \end{array}\begin{array}{*{20}c} { t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$

It can be seen that:

• $h_{\rm g}(t) = h_{\rm u}(t) = h(t)/2$ holds for positive times.
• $h_{\rm g}(t)$  and  $h_{\rm u}(t)$  differ only by the sign for negative times.
• $h(t) = h_{\rm g}(t) + h_{\rm u}(t)$ holds for all times, also at time  $t = 0$ (marked by circles).

Let us now consider the same issue in the spectral domain. According to the  Assignment Theorem  the following holds for the complex transfer function:  

$$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} ,$$

where the following assignment holds:

$${\rm Re} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm g}}(t)\hspace{0.05cm},$$

$${\rm j} \cdot {\rm Im} \left\{ H(f) \right\} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm u}}(t)\hspace{0.05cm}.$$

First, this relationship between the real and imaginary parts of  $H(f)$  shall be worked out using another example.

$\text{Example 2:}$  A low-pass filter of first-order is assumed and the following holds for its transfer function:

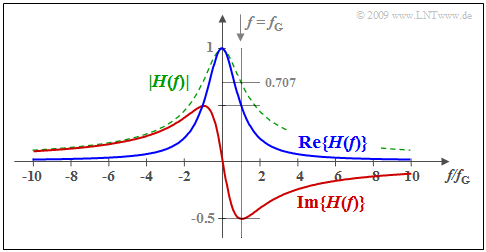
$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G} } = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$

Here,  $f_{\rm G}$  represents the 3dB cut-off frequency at which  $\vert H(f)\vert^2$  has decreased to half of its maximum  $($at  $f = 0)$ . The corresponding impulse response  $h(t)$  has already been shown in the above  $\text{Example 1}$  for  $f_{\rm G} = 1/(2πT)$ .

The graph shows the real part (blue) and the imaginary part (red) of  $H(f)$. In addition, the magnitude is shown dashed in green.

Frequency response of a low-pass filter of first-order  (real and imaginary part)

Since the time functions  $h_{\rm g}(t)$  and  $h_{\rm u}(t)$  are related by the sign function, there also exists a fixed relationship

• between the real part   ⇒   ${\rm Re} \{H(f)\}$ 
• and the imaginary part   ⇒  ${\rm Im} \{H(f)\}$ 

of the transfer function

          ⇒   the  Hilbert transformation.

This is described below.

Hilbert transformation

Here, two time functions  $u(t)$  and  $w(t) = \sign(t) · u(t)$ are considered in the most general sense.

• The associated spectral functions are denoted by  $U(f)$  and  ${\rm j} · W(f)$ .
• That is, in this section  ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {\rm j} \cdot W(f) }$  is valid and not the usual Fourier correspondence  ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, W(f)}.$

Using the correspondence   ${\rm sign}(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {1}/({{\rm j} \, \pi f })$   the following is obtained after writing the convolution integral out in full with the integration variable  $ν$ :

$${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

However, since at the same time   $u(t) = \sign(t) · w(t)$   also holds, the following is valid in the same way:

$$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

These integral transformations  are named after their discoverer  David Hilbert .

$\text{Definition:}$  Both variants of the  Hilbert transformation  will be denoted by the following abbreviations in the further course:

$$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.8cm}{\rm or}\hspace{0.8cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$

• To calculate the spectrum marked by the arrowhead – here  $U(f)$  – the equation with the positive sign is taken from the two otherwise identical upper equations:

$$U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

• The spectrum marked by the circle – here  $W(f)$  – arises as a result from the equation with the negative sign:

$$ W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

Applying the Hilbert transformation twice yields the original function with a change of sign, and applying it four times yields the original function including the correct sign:

$${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f), \hspace{0.2cm} {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$

$\text{Example 3:}$  In  [Mar94]  the following Hilbert correspondence can be found:

$$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$

• Here  $x$  is representative of a suitably normalized time or frequency variable.
• For example, if we use  $x = f/f_{\rm G}$  as a normalized frequency variable, then we obtain the correspondence:

$$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

Based on the equation

$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$

the result found in  $\text{Example 2}$  is thus confirmed:

$${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

Some pairs of Hilbert correspondences

Zur Herleitung von Hilbert–Korrespondenzen geht man sehr pragmatisch vor, nämlich wie folgt:

• The  Laplace transform  $Y_{\rm L}(p)$  of the function  $y(t)$ is computed as described below. This is already implicitly causal.
• The spectral function  $Y_{\rm L}(p)$  is converted into the associated Fourier spectrum  $Y(f)$  which is split it into real and imaginary parts.  To do this, the variable  $p$  is replaced by  ${\rm j \cdot 2}πf.$
• The real– and imaginary parts – so  ${\rm Re} \{Y(f)\}$  and  ${\rm Im} \{Y(f)\}$ – are thus a pair of Hilbert transforms. Furthermore,
  • the frequency variable  $f$  is substituted by  $x$,
  • ${\rm Re} \{Y(f)\}$  by  $g(x)$, and
  • ${\rm Im} \{Y(f)\}$  by  ${\cal H} \{g(x)\}$.

• The new variable  $x$  can describe both a (suitably) normalized frequency or a (suitably) normalized time. Hence, the  Hilbert transformation  is applicable to various problems.

Table with Hilbert correspondences

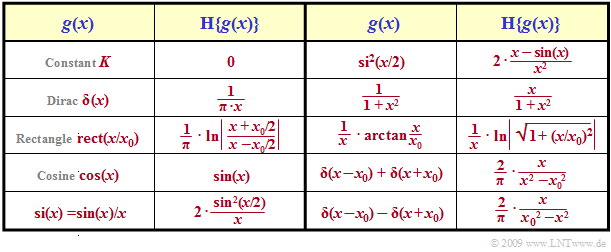
Die Tabelle zeigt einige solcher Hilbertpaare.   Auf die Vorzeichen wurde verzichtet, so dass beide Richtungen gültig sind.

$\text{Example 4:}$  Gilt beispielsweise  ${\cal H} \{g(x)\} = f(x)$, so folgt daraus auch  ${\cal H} \{f(x)\} = \, –g(x)$. Insbesondere gilt auch:

$${\cal H}\left \{ \cos(x) \right\} = \sin(x)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\cal H}\left \{ \sin(x) \right\} = -\cos(x)\hspace{0.05cm}.$$

Dämpfung und Phase von Minimum–Phasen–Systemen

Eine wichtige Anwendung der Hilbert–Transformation stellt der Zusammenhang zwischen Dämpfung und Phase bei den so genannten Minimum–Phasen–Systemen  dar. Im Vorgriff auf das folgende Kapitel  Laplace–Transformation und p–Übertragungsfunktion  sei erwähnt, dass diese Systeme in der rechten  $p$–Halbebene weder Pole noch Nullstellen aufweisen dürfen.

Allgemein gilt für die Übertragungsfunktion  $H(f)$  mit dem  komplexen Übertragungsmaß  $g(f)$  sowie der Dämpfungsfunktion  $a(f)$  und der Phasenfunktion  $b(f)$:

$$H(f) = {\rm e}^{-g(f)} = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} g(f) = a(f)+ {\rm j} \cdot b(f)\hspace{0.05cm}.$$

Bei den Minimum–Phasen–Systemen gilt nun aber nicht nur wie bei allen realisierbaren Systemen die Hilbert–Transformation

• bezüglich Imaginär– und Realteil   ⇒   ${\rm Im} \left\{ H(f) \right \} \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, {\rm Re} \left\{ H(f) \right \}\hspace{0.01cm},$
• sondern zusätzlich auch noch die Hilbert–Korrespondenz zwischen der Phasen– und der Dämpfungsfunktion   ⇒   $b(f) \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, a(f)\hspace{0.05cm}.$

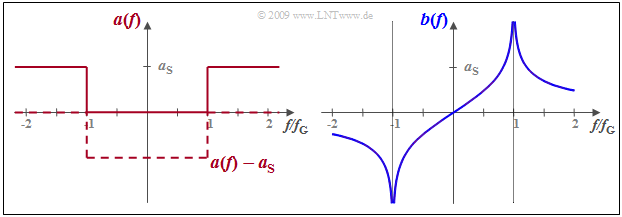
$\text{Example 5:}$  Ein Tiefpass besitze im Durchlassbereich – also für  $\vert f \vert < f_{\rm G}$ – den Frequenzgang  $H(f) = 1$   ⇒   $a(f) =0 \ {\rm Np}$, während für größere Frequenzen die Dämpfungsfunktion  $a(f)$  den konstanten Wert  $a_{\rm S}$ (in Neper) besitzt.

In diesem Sperrbereich ist  $H(f) = {\rm e}^{–a_{\rm S} }$  zwar sehr klein, aber nicht Null.

Dämpfungs– und Phasenfunktion eines beispielhaften Minimum–Phasen–Tiefpasses

• Soll der Tiefpass kausal und damit realisierbar sein, so muss die Phasenfunktion  $b(f)$  gleich der Hilbert–Transformierten der Dämpfung  $a(f)$  sein.
• Da die Hilbert–Transformierte einer Konstanten gleich Null ist, kann in gleicher Weise von der Funktion  $a(f) - a_{\rm S}$  ausgegangen werden.

Diese in der Grafik gestrichelt eingezeichnete Funktion ist zwischen  $±f_{\rm G}$  (negativ) rechteckförmig. Entsprechend der  Tabelle  auf der letzten Seite gilt deshalb:

$$b(f) = {a_{\rm S} }/{\pi} \cdot {\rm ln}\hspace{0.1cm}\left\vert \frac{f+f_{\rm G} }{f-f_{\rm G} }\right \vert \hspace{0.05cm}.$$

Jeder andere Phasenverlauf würde dagegen zu einer akausalen Impulsantwort führen.

Exercises for the chapter

Exercise 3.1: Kausalitätsbetrachtungen

Exercise 3.1Z: Hilbert-Transformierte