Redundancy-Free Coding

1. Digital Signal Transmission
2. Coded and Multilevel Transmission
3. Redundancy-Free Coding

• Previous page
• Next page

• Previous page
• Next page

Symbolwise coding vs. blockwise coding

In transmission coding,  a distinction is made between two fundamentally different methods:

Symbolwise coding

• Here,  a code symbol  $c_\nu$  is generated with each incoming source symbol  $q_\nu$,  which can depend not only on the current symbol but also on previous symbols  $q_{\nu -1}$,  $q_{\nu -2}$, ...
  

• It is typical for all transmission codes for symbolwise coding that the symbol duration  $T_c$  of the usually multilevel and redundant encoder signal  $c(t)$  corresponds to the bit duration  $T_q$  of the source signal,  which is assumed to be binary and redundancy-free.
  

Details can be found in the chapter  "Symbolwise Coding with Pseudo-Ternary Codes".

Blockwise coding

• Here,  a block of  $m_q$  binary source symbols  $(M_q = 2)$  of bit duration  $T_q$  is assigned a one-to-one sequence of  $m_c$  code symbols from an alphabet with code symbol set size  $M_c \ge 2$. 

• For the  symbol duration of a code symbol  then holds:

$$T_c = \frac{m_q}{m_c} \cdot T_q \hspace{0.05cm},$$

• The  relative redundancy of a block code  is in general

$$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.05cm}.$$

More detailed information on the block codes can be found in the chapter  "Block Coding with 4B3T Codes".

$\text{Example 1:}$  For the  "pseudo-ternary codes"',  increasing the number of levels from  $M_q = 2$  to  $M_c = 3$  for the same symbol duration  $(T_c = T_q)$  adds a relative redundancy of  $r_c = 1 - 1/\log_2 \hspace{0.05cm} (3) \approx 37\%$. 

In contrast,  the so-called  "4B3T codes"  operate at block level with the code parameters  $m_q = 4$,  $M_q = 2$,  $m_c = 3$  and  $M_c = 3$  and have a relative redundancy of approx.  $16\%$.  Because of  ${T_c}/{T_q} = 4/3$,  the transmitted signal  $s(t)$  is lower in frequency here than in uncoded transmission, which reduces the expensive bandwidth and is also advantageous for many channels from a transmission point of view.

Quaternary signal with  $r_{\rm c} \equiv 0$  and ternary signal with  $r_{\rm c} \approx 0$

A special case of a block code is a  redundancy-free multilevel code. 

• Starting from the redundancy-free binary source signal  $q(t)$  with bit duration  $T_q$, 
• a  $M_c$–level code signal  $c(t)$  with symbol duration  $T_c = T_q \cdot \log_2 \hspace{0.05cm} (M_c)$  is generated.

Thus,  the relative redundancy is given by:

$$r_c = 1- \frac{T_c}{T_q \cdot {\rm log_2}\hspace{0.05cm} (M_c)} = 1- \frac{m_q}{m_c \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\to 0 \hspace{0.05cm}.$$

Thereby holds:

1. If  $M_c$  is a power to the base  $2$,  then  $m_q = \log_2 \hspace{0.05cm} (M_c)$  are combined into a single code symbol  $(m_c = 1)$.  In this case, the relative redundancy is actually  $r_c = 0$.
   
2. If  $M_c$  is not a power of two,  a hundred percent redundancy-free block coding is not possible.  For example, if  $m_q = 3$  binary symbols are encoded by  $m_c = 2$  ternary symbols and  $T_c = 1.5 \cdot T_q$  is set,  a relative redundancy of  $r_c = 1-1.5/ \log_2 \hspace{0.05cm} (3) \approx 5\%$  remains.
   
3. Encoding a block of  $128$  binary symbols with  $81$  ternary symbols results in a relative code redundancy of less than  $r_c = 0.3\%$.
   
   

To simplify the notation and to align the nomenclature with the "first main chapter",  we use in the following

• the bit duration  $T_{\rm B} = T_q$  of the redundancy-free binary source signal,
• the symbol duration  $T = T_c$  of the encoder signal and the transmitted signal, and
• the number  $M = M_c$  of levels.
  

This results in the identical form for the transmitted signal as for the binary transmission,  but with different amplitude coefficients:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm with}\hspace{0.3cm} a_\nu \in \{ a_1, \text{...} , a_\mu , \text{...} , a_{ M}\}\hspace{0.05cm}.$$

• In principle,  the amplitude coefficients  $a_\nu$  can be assigned arbitrarily  – but uniquely –  to the encoder symbols  $c_\nu$.  It is convenient to choose equal distances between adjacent amplitude coefficients.

• Thus,  for bipolar signaling  $(-1 \le a_\nu \le +1)$,  the following applies to the possible amplitude coefficients with index  $\mu = 1$, ... , $M$:

$$a_\mu = \frac{2\mu - M - 1}{M-1} \hspace{0.05cm}.$$

• Independently of the level number  $M$  one obtains from this for the outer amplitude coefficients  $a_1 = -1$  and  $a_M = +1$.

• For a ternary signal  $(M = 3)$,  the possible amplitude coefficients are  $-1$,  $0$  and  $+1$.

• For a quaternary signal  $(M = 4)$,  the coefficients are  $-1$,  $-1/3$,  $+1/3$  and  $+1$.
  

$\text{Example 2:}$  The graphic above shows the quaternary redundancy-free transmitted signal  $s_4(t)$  with the possible amplitude coefficients  $\pm 1$  and  $\pm 1/3$,  which results from the binary source signal  $q(t)$  shown in the center.

Redundancy-free ternary and quaternary signal

• Two binary symbols each are combined to a quaternary coefficient according to the table with red background. The symbol duration  $T$  of the signal  $s_4(t)$  is twice the bit duration  $T_{\rm B}$  $($previously:  $T_q)$  of the source signal.

• If  $q(t)$  is redundancy-free, it also results in a redundancy-free quaternary signal, i.e., the possible amplitude coefficients  $\pm 1$  and  $\pm 1/3$  are equally probable and there are no statistical ties within the sequence  $⟨a_ν⟩$. 

The lower plot shows the $($almost$)$ redundancy-free ternary signal  $s_3(t)$  and the mapping of three binary symbols each to two ternary symbols.

• The possible amplitude coefficients are  $-1$,  $0$  and  $+1$  and the symbol duration of the coded signal  $T = 3/2 \cdot T_{\rm B}$.

• It can be seen from the green mapping table that the coefficients  $+1$  and  $-1$  occur somewhat more frequently than the coefficient  $a_\nu = 0$.  This results in the above mentioned relative redundancy of  $5\%$.

• However,  from the very short signal section  – only eight ternary symbols corresponding to twelve binary symbols –  this property is not apparent.

ACF and PSD of a multilevel signal

For a redundancy-free coded  $M$–level bipolar digital signal  $s(t)$,  the following holds for the  "discrete auto-correlation function"  $\rm (ACF)$  of the amplitude coefficients and for the corresponding  "power-spectral density"  $\rm (PSD)$:

$$\varphi_a(\lambda) = \left\{ \begin{array}{c} \frac{M+ 1}{3 \cdot (M-1)} \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\\ \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \\ \end{array} \hspace{0.9cm}\Rightarrow \hspace{0.9cm}{\it \Phi_a(f)} = \frac{M+ 1}{3 \cdot (M-1)}= {\rm const.}$$

Considering the spectral shaping by the basic transmission pulse  $g_s(t)$  with spectrum  $G_s(f)$,  we obtain:

$$\varphi_{s}(\tau) = \frac{M+ 1}{3 \cdot (M-1)} \cdot \varphi^{^{\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_{s}(f) = \frac{M+ 1}{3 \cdot (M-1)}\cdot |G_s(f)|^2 \hspace{0.05cm}.$$

One can see from these equations:

• In the case of redundancy-free multilevel coding,  the shape of ACF and PSD is determined solely by the basic transmission pulse  $g_s(t)$. 
  

• The magnitude of the ACF is lower than the redundancy-free binary signal by a factor  $\varphi_a(\lambda = 0) = {\rm E}\big[a_\nu^2\big] = (M + 1)/(3M-3)$  for the same shape.
  

• This factor describes the lower signal power of the multilevel signal due to the  $M-2$  inner amplitude coefficients.  For  $M = 3$  this factor is equal to  $2/3$, for  $M = 4$  it is equal to  $5/9$.
  

• However,  a fair comparison between binary and multilevel signal with the same information flow  (same equivalent bit rate)  should also take into account the different symbol durations.  This shows that a multilevel signal requires less bandwidth than the binary signal due to the narrower PSD when the same information is transmitted.
  
  

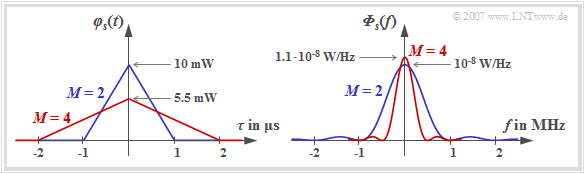
$\text{Example 3:}$  We assume a binary source with bit rate  $R_{\rm B} = 1 \ \rm Mbit/s$,  so that the bit duration  $T_{\rm B} = 1 \ \rm µ s$. 

Auto-correlation function and power-spectral density of binary and quaternary signal

• For binary transmission  $(M = 2)$,  the symbol duration of the transmitted signal is  $T =T_{\rm B}$  and the auto-correlation function shown in blue in the left graph results for NRZ rectangular pulses (assuming  $s_0^2 = 10 \ \rm mW$).
• For the quaternary system  $(M = 4)$,  the ACF is also triangular, but lower by a factor of  $5/9$  and twice as wide because of  $T = 2 \cdot T_{\rm B}$. 

The  $\rm sinc^2$–shaped power-spectral density in the binary case  (blue curve)  has the maximum value  ${\it \Phi}_{s}(f = 0) = 10^{-8} \ \rm W/Hz$  (area of the blue triangle)  for the signal parameters selected here.  The first zero point is at  $f = 1 \ \rm MHz$.

• The PSD of the quaternary signal  (red curve)  is only half as wide and slightly higher.  Here:  ${\it \Phi}_{s}(f = 0) \approx 1.1 \cdot 10^{-8} \ \rm W/Hz$.
• The value results from the area of the red triangle. 
  This is lower  $($factor  $0.55)$  and wider (factor $2$).

Error probability of a multilevel system

Eye diagrams for redundancy–free binary, ternary and quaternary signals

The diagram on the right shows the eye diagrams

• of a binary transmission system  $(M = 2)$,
• a ternary transmission system  $(M = 3)$ and
• a quaternary transmission system  $(M = 4)$.

Here,  a cosine rolloff characteristic is assumed for the overall system  $H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f)$  of transmitter, channel and receiver,  so that intersymbol interference does not play a role.  The rolloff factor is  $r= 0.5$.  The noise is assumed to be negligible.

The eye diagram is used to estimate intersymbol interference.  A detailed description follows in the section  "Definition and statements of the eye diagram".  However,  the following text should be understandable even without detailed knowledge.

It can be seen from the above diagrams:

• In the  binary system   $(M = 2)$,  there is only one decision threshold:   $E_1 = 0$.  A transmission error occurs if the noise component  $d_{\rm N}(T_{\rm D})$  at the detection time is greater than  $+s_0$   $\big ($if  $d_{\rm S}(T_{\rm D}) = -s_0$ $\big )$  or  if  $d_{\rm N}(T_{\rm D})$  is less than  $-s_0$   $\big ($if  $d_{\rm S}(T_{\rm D}) = +s_0$ $\big )$.
  

• In the case of the  ternary system  $(M = 3)$,  two eye openings and two decision thresholds  $E_1 = -s_0/2$  and  $E_2 = +s_0/2$  can be recognized.  The distance of the possible useful detection signal values  $d_{\rm S}(T_{\rm D})$  to the nearest threshold is  $-s_0/2$ in each case.  The outer amplitude values  $(d_{\rm S}(T_{\rm D}) = \pm s_0)$  can only be falsified in one direction in each case,  while  $d_{\rm S}(T_{\rm D}) = 0$  is limited by two thresholds.
  

• Accordingly,  an amplitude coefficient  $a_\nu = 0$  is falsified twice as often compared to  $a_\nu = +1$  or  $a_\nu = -1$.  For AWGN noise with rms value  $\sigma_d$  as well as equal probability amplitude coefficients,  according to the section  "Definition of the bit error probability"  for the  "symbol error probability":

$$p_{\rm S} = { 1}/{3} \cdot \left[{\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)+ 2 \cdot {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)+ {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)\right]= \frac{ 4}{3} \cdot {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)\hspace{0.05cm}.$$

• Please note that this equation no longer specifies the bit error probability  $p_{\rm B}$, but the  "symbol error probability"  $p_{\rm S}$.  The corresponding a posteriori parameters are  "bit error rate"  $\rm (BER)$  and  "symbol error rate"  $\rm (SER)$.  More details are given in the  "last section"  of this chapter.
  

For the quaternary system  $(M = 4)$  with the possible amplitude values  $\pm s_0$  and  $\pm s_0/3$, 

• there are three eye-openings,  and
• thus also three decision thresholds at  $E_1 = -2s_0/3$,  $E_2 = 0$  and  $E_3 = +2s_0/3$.

Taking into account the occurrence probabilities  $(1/4$  for equally probable symbols$)$  and the six possibilities of falsification (see arrows in the graph),  we obtain:

$$p_{\rm S} = { 6}/{4} \cdot {\rm Q} \left( \frac{s_0/3}{\sigma_d}\right)\hspace{0.05cm}.$$

$\text{Conclusion:}$  In general, the  symbol error probability  for  $M$–level digital signal transmission is:

$$p_{\rm S} = \frac{ 2 + 2 \cdot (M-2)}{M} \cdot {\rm Q} \left( \frac{s_0/(M-1)}{\sigma_d(M)}\right) = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \frac{s_0}{\sigma_d (M)\cdot (M-1)}\right)\hspace{0.05cm}.$$

• The notation  $\sigma_d(M)$  is intended to make clear that the rms value of the noise component  $d_{\rm N}(t)$  depends significantly on the number  $M$. 

Comparison between binary system and multilevel system

For this system comparison under fair conditions,  the following are assumed:

• Let the equivalent bit rate  $R_{\rm B} = 1/T_{\rm B}$  be constant.  Depending on the number  $M$,  the symbol duration of the encoder signal and the transmitted signal is thus:

$$T = T_{\rm B} \cdot {\rm log_2} (M) \hspace{0.05cm}.$$

• The Nyquist condition is satisfied by a  "root–root characteristic"  with rolloff factor  $r$.  Furthermore,  no intersymbol interference occurs.  The detection noise power is:

$$\sigma_d^2 = \frac{N_0}{2T} \hspace{0.05cm}.$$

• The comparison of the symbol error probabilities  $p_{\rm S}$  is performed for  "power limitation". The energy per bit for  $M$–level transmission is:

$$E_{\rm B} = \frac{M+ 1}{3 \cdot (M-1)} \cdot s_0^2 \cdot T_{\rm B} \hspace{0.05cm}.$$

Substituting these equations into the general result on the  "last section",  we obtain for the symbol error probability:

$$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \sqrt{\frac{s_0^2 /(M-1)^2}{\sigma_d^2}}\right) = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \sqrt{\frac{3 \cdot {\rm log_2}\hspace{0.05cm} (M)}{M^2 -1}\cdot \frac{2 \cdot E_{\rm B}}{N_0}}\right)$$

Symbol error probability curves for different level numbers  $M$

$$\Rightarrow \hspace{0.3cm} p_{\rm S} = K_1 \cdot {\rm Q} \left( \sqrt{K_2\cdot \frac{2 \cdot E_{\rm B}}{N_0}}\right)\hspace{0.05cm}.$$

For  $M = 2$,  set  $K_1 = K_2 = 1$.  For larger level numbers,  one obtains for the symbol error probability that can be achieved with  $M$–level redundancy-free coding:

$$M = 3\text{:} \ \ K_1 = 1.333, \ K_2 = 0.594;\hspace{0.5cm}M = 4\text{:} \ \ K_1 = 1.500, \ K_2 = 0.400;$$

$$M = 5\text{:} \ \ K_1 = 1.600, \ K_2 = 0.290;\hspace{0.5cm}M = 6\text{:} \ \ K_1 = 1.666, \ K_2 = 0.221;$$

$$M = 7\text{:} \ \ K_1 = 1.714, \ K_2 = 0.175;\hspace{0.5cm}M = 8\text{:} \ \ K_1 = 1.750, \ K_2 = 0.143.$$

The graph summarizes the results for  $M$–level redundancy-free coding.

• Plotted are the symbol error probabilities  $p_{\rm S}$  over the abscissa  $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0)$.

• All systems are optimal for the respective  $M$,  assuming the AWGN channel and power limitation.

• Due to the double logarithmic representation chosen here, a  $K_2$ value smaller than  $1$  leads to a parallel shift of the error probability curve to the right.

• If  $K_1 > 1$ applies, the curve shifts upwards compared to the binary system  $(K_1= 1)$. 
  

$\text{System comparison under the constraint of power limitation:}$  The above curves can be interpreted as follows:

1. Regarding symbol error probability,  the binary system  $(M = 2)$  is superior to the multilevel systems.  Already with  $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) = 12 \ \rm dB$  one reaches  $p_{\rm S} <10^{-8}$.  For the quaternary system  $(M = 4)$,   $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) > 16 \ \rm dB$  must be spent to reach the same symbol error probability  $p_{\rm S} =10^{-8}$. 
2. However,  this statement is valid only for distortion-free channel,  i.e., for  $H_{\rm K}(f)= 1$.  On the other hand,  for distorting transmission channels,  a higher-level system can provide a significant improvement because of the significantly smaller noise component of the detection signal  (after the equalizer).
   
3. For the AWGN channel,  the only advantage of a higher-level transmission is the lower bandwidth requirement due to the smaller equivalent bit rate,  which plays only a minor role in baseband transmission in contrast to digital carrier frequency systems,  e.g.  "quadrature amplitude modulation"  $\rm (QAM)$.

$\text{System comparison under the peak limitation constraint:}$ 

• With the constraint  "peak limitation",  the combination of rectangular  $g_s(t)$  and rectangular  $h_{\rm E}(t)$  leads to the optimum regardless of the level number  $M$. 
  

• The loss of the multilevel system compared to the binary system is here even greater than with power limitation.

• This can be seen from the factor  $K_2$  decreasing with  $M$,  for which then applies:

$$p_{\rm S} = K_1 \cdot {\rm Q} \left( \sqrt{K_2\cdot \frac{2 \cdot s_{\rm 0}^2 \cdot T}{N_0} }\right)\hspace{0.3cm}{\rm with}\hspace{0.3cm} K_2 = \frac{ {\rm log_2}\,(M)}{(M-1)^2} \hspace{0.05cm}.$$

• The constant  $K_1$  is unchanged from the above specification for power limitation,  while  $K_2$  is smaller by a factor of  $3$: 

$$M = 3\text{:} \ \ K_1 = 1.333, \ K_2 = 0.198;\hspace{1cm}M = 4\text{:} \ \ K_1 = 1.500, \ K_2 = 0.133;$$

$$M = 5\text{:} \ \ K_1 = 1.600, \ K_2 = 0.097;\hspace{1cm}M = 6\text{:} \ \ K_1 = 1.666, \ K_2 = 0.074;$$

$$M = 7\text{:} \ \ K_1 = 1.714, \ K_2 = 0.058;\hspace{1cm}M = 8\text{:} \ \ K_1 = 1.750, \ K_2 = 0.048.$$

Symbol and bit error probability

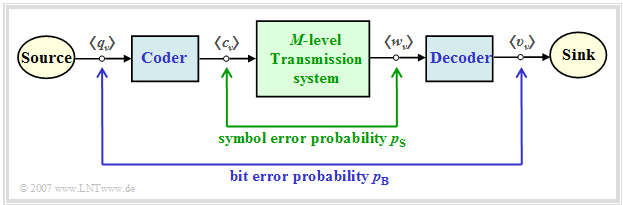
In a multilevel transmission system,  one must distinguish between the  "symbol error probability"  and the  "bit error probability",  which are given here both as ensemble averages and as time averages:

Symbol error probability and bit error probability

• The  symbol error probability  refers to the  $M$–level and possibly redundant sequences  $\langle c_\nu \rangle$  and  $\langle w_\nu \rangle$:

$$p_{\rm S} = \overline{{\rm Pr} (w_\nu \ne c_\nu)} = \lim_{N \to \infty} \frac{1}{N} \cdot \sum \limits^{N} _{\nu = 1} {\rm Pr} (w_\nu \ne c_\nu) \hspace{0.05cm}.$$

• The  bit error probability  describes the falsifications with respect to the binary sequences  $\langle q_\nu \rangle$  and  $\langle v_\nu \rangle$  of source and sink:

$$p_{\rm B} = \overline{{\rm Pr} (v_\nu \ne q_\nu)} = \lim_{N \to \infty} \frac{1}{N} \cdot \sum \limits^{N} _{\nu = 1} {\rm Pr} (v_\nu \ne q_\nu) \hspace{0.05cm}.$$

The diagram illustrates these two definitions and is also valid for the next chapters.  The block  "coder"  causes

• in the present chapter a redundancy-free coding,
• in the  "following chapter"  a blockwise transmission coding,  and finally
• in the  "last chapter"  symbolwise coding with pseudo-ternary codes.

$\text{Conclusion:}$ 

• For multilevel and/or coded transmission,  a distinction must be made between the bit error probability  $p_{\rm B}$  and the symbol error probability  $p_{\rm S}$.  Only in the case of the redundancy-free binary system does  $p_{\rm B} = p_{\rm S}$ apply.

• In general,  the symbol error probability  $p_{\rm S}$  can be calculated somewhat more easily than the bit error probability  $p_{\rm B}$  for redundancy-containing multilevel systems.

• However,  a comparison of systems with different level numbers  $M$  or different types of coding should always be based on the bit error probability  $p_{\rm B}$  for reasons of fairness.  The mapping between the source and coded symbols must also be taken into account,  as shown in the following example.

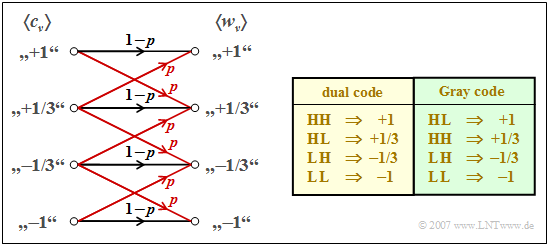
$\text{Example 4:}$  We consider a quaternary transmission system whose transmission behavior can be characterized as follows  (see left sketch in the graphic):

• The falsification probability to a neighboring symbol is  

$$p={\rm Q}\big [s_0/(3\sigma_d)\big ].$$

• A falsification to a non-adjacent symbol is excluded.
  
• The model considers the dual falsification possibilities of inner symbols.
  

For equally probable binary source symbols  $q_\nu$  the quaternary code symbols  $c_\nu$  also occur with equal probability.  Thus,  we obtain for the symbol error probability:

$$p_{\rm S} ={1}/{4}\cdot (2 \cdot p + 2 \cdot 2 \cdot p) = {3}/{2} \cdot p\hspace{0.05cm}.$$

Comparison of dual code and Gray code

To calculate the bit error probability,  one must also consider the mapping between the binary and the quaternary symbols:

• In  "dual coding"  according to the table with yellow background,  one symbol error  $(w_\nu \ne c_\nu)$  can result in one or two bit errors  $(v_\nu \ne q_\nu)$.  Of the six corruption possibilities at the quaternary symbol level,  four result in one bit error each and only the two inner ones result in two bit errors.  It follows:

$$p_{\rm B} = {1}/{4}\cdot (4 \cdot 1 \cdot p + 2 \cdot 2 \cdot p ) \cdot {1}/{2} = p\hspace{0.05cm}.$$

The factor  $1/2$  takes into account that a quaternary symbol contains two binary symbols.

• In contrast,  in the so-called  "Gray coding"  according to the table with green background,  the mapping between the binary symbols and the quaternary symbols is chosen in such a way that each symbol error results in exactly one bit error. From this follows:

$$p_{\rm B} = {1}/{4}\cdot (4 \cdot 1 \cdot p + 2 \cdot 1 \cdot p ) \cdot {1}/{2} = {3}/{4} \cdot p\hspace{0.05cm}.$$

Exercises for the chapter

Exercise 2.3: Binary Signal and Quaternary Signal

Exercise 2.4: Dual Code and Gray Code

Exercise 2.4Z: Error Probabilities for the Octal System

Exercise 2.5: Ternary Signal Transmission