Viterbi Receiver

1 Considered scenario and prerequisites
2 Error sizes and total error sizes
3 Minimale Gesamtfehlergrößen
4 Darstellung der minimalen Gesamtfehlergrößen – Trellisdiagramm
5 Vereinfachtes Trellisdiagramm
6 Erweiterung auf zwei Vorläufer
7 Error probability in maximum likelihood decision
8 Aufgaben zum Kapitel

Considered scenario and prerequisites

The "correlation receiver" is optimal in the sense of the "maximum likelihood decision rule", that is, it leads to the minimum error probability for equally likely source symbols. Disadvantage:

The realization cost increases exponentially with the length $N$ of the symbol sequence to be detected.
Since the sequence is decided jointly, long delays occur when $N$ is large.

In the 1970s, "Andrew J. Viterbi" proposed a maximum likelihood receiver that allows detection of parts of the received message and for which the implementation cost is limited even for infinitely long sequences.

Block diagram of the Viterbi receiver

It should be noted with regard to the individual components of the block diagram:

Adjusted to the basic reception pulse $g_r(t)$ and the noise, the "matched filter" $H_{\rm MF}(f)$ serves for noise power limitation. The MF output signal $m(t)$ or the sequence $\langle m_\nu \rangle$ of equidistant signal values after sampling has the best possible signal-to-noise power ratio.

The task of the decorrelation filter $H_{\rm DF}(f)$ is to extract from the sequence $\langle m_\nu \rangle$ the detection samples $d_\nu = d_{{\rm S}\nu} + d_{{\rm N}\nu}$ whose noise components $d_{{\rm N}\nu}$ are uncorrelated. This filter is therefore also called a whitening filter.

The Viterbi decision, which is the focus of the following considerations, obtains the binary output sequence $\langle v_\nu \rangle$ ; from the sequence $\langle d_\nu \rangle$&nbsp of its continuous value input values according to the maximum likelihood rule with the smallest possible error probability ${\rm Pr}(v_\nu \ne q_\nu)$.

In order to describe the Viterbi algorithm as simply as possible, some simplifying assumptions are made here:

Let the amplitude coefficients be unipolar ⇒ $a_\nu \in \{0,\hspace{0.05cm} 1\}$. Note that using bipolar coefficients ⇒ $a_\nu \in \{-1,\hspace{0.05cm} +1\}$ requires only a few modifications. These difficulties concern the description rather than the implementation.

The basic pulse $g_d(t)$ consists only of the main value $g_0 = g_d(t = T_{\rm D})$ and a single precursor $g_{-1} = g_d(t = T_{\rm D}-T)$.

This gives $d_{\nu} = a_{\nu}\cdot g_{0} + a_{\nu+1}\cdot g_{-1}+d_{{\rm N}\nu}\hspace{0.05cm}$ for the continuous-value detection samples, where the noise component $d_{{\rm N}\nu}$ is assumed to be Gaussian distributed with standard deviation $\sigma_d$.

Note: With bipolar signaling, the algorithm is not more complex. In contrast, the computational cost increases when the basic detection pulse becomes broader and has more than one precursor $g_{-1}$. The neglect of precursors in the description is not a fundamental limitation because any pulse $g_d(t)$ can satisfy this condition by appropriate choice of the detection time $T_{\rm D}$. It should be further noted that in the following all signal values are normalized to $1$.

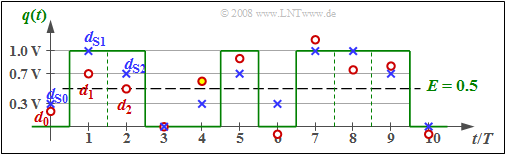
Sampling values to illustrate the Viterbi algorithm

$\text{Example 1:}$ In the graph, the detection useful samples $d_{ {\rm S}\nu}$ are entered as (blue) crosses, where the corresponding amplitude coefficients $a_1 = 1$, $a_2 = 1$, $a_3 = 0$, ... can be read from the source signal $q(t)$ plotted in green.

The basic pulse values in this example are assumed to be $g_0 = 0.7$ and $g_{-1} = 0.3$. It can be further seen that $d_{ {\rm S}\nu}$ can take only four different values, namely $0$, $g_{-1}=0.3$, $g_0= 0.7$ and $g_0 +g_{-1}= 1$.

The samples present at the Viterbi decision (red dots) are $d_0 = 0.2$, $d_1 = 0.7$, $d_2 = 0.5$, $d_3 = 0$, ... , where the differences $d_{ {\rm N}\nu} = d_\nu - d_{ {\rm S}\nu}$ originate from an AWGN noise source.

A threshold decision $($with the threshold at $E = 0.5)$ would make at least one wrong decision at these ten bits shown $($at time $t = 4T)$, and possibly another at $t = 2T$ if the sample $d_2 = 0.5$ is nevertheless slightly smaller than the threshold $E = 0.5$.
In contrast, the Viterbi receiver will correctly decide this sequence of length $10$, as shown in the next sections.

Error sizes and total error sizes

As in the chapter "Optimal Receiver Strategies", $Q \in \{Q_i\}$ specifies the bounded source symbol sequence consisting of $N$ binary symbols.

Thus, the number of possible symbol sequences $Q_i$ is $2^N$.
$V$ denotes the sink symbol sequence of length $N$ set equal to the most probable sequence $Q_j$ by the Viterbi decision.

$\text{Definition:}$ The error quantity $\varepsilon_{\nu}(i)$ denotes the squared deviation between the actual, noisy sample $d_\nu$ and the useful sample $d_{ {\rm S}\nu}$ belonging to the sequence $Q_i$:

$$\varepsilon_{\nu}(i) = \vert d_{\nu} - d_{ {\rm S}\nu}(i) \vert^2 \hspace{0.05cm}.$$

In the literature, this is also referred to as "metric".

$\text{Definition:}$ The total error quantity $\gamma_{\nu}(i)$ characterizes the sum of all error quantities up to time $\nu$:

$$\gamma_{\nu}(i)= \sum_{k=0}^{\nu}\varepsilon_{k}(i) \hspace{0.05cm}.$$

In this context, one also speaks of the "accumulated metric".

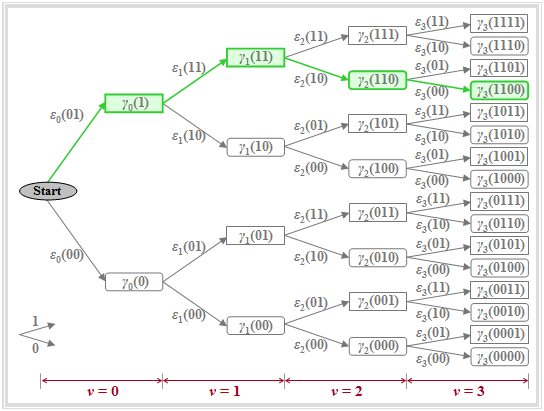
Representation of the error quantities and accumulated error quantities in the tree diagram

The graph illustrates the quantities defined above in a tree structure, from which it can be seen that the total error quantities can be calculated iteratively:

$$\gamma_{\nu}(i)= \gamma_{\nu-1}(i\hspace{0.05cm}')+\varepsilon_{\nu}(i\hspace{0.05cm}'') \hspace{0.05cm}.$$

Notes:

$i$, $i\hspace{0.05cm}'$, $i\hspace{0.05cm}''$ sind unterschiedliche Laufvariable.
Obige Definition gilt für einen Grundimpuls mit Hauptwert $g_{0}$ und einem Vorläufer $g_{-1}$.
Bei $v$ Vorläufern müsste die obige Summe bei $k = 1 -v$ beginnen.
Der Parameter $i \in \{0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, 2^{N+1}-1\}$ wird meist binär dargestellt und beschreibt so die Amplitudenkoeffizienten $a_1$, ... , $a_{\nu +1}$ $($jeweils $0$ oder $1)$.

Weiter ist zu dieser Grafik anzumerken:

Die Knoten des Baumdiagramms stehen für die Gesamtfehlergrößen $\gamma_{\nu}(i)$. Deren Anzahl wird mit jedem Iterationsschritt verdoppelt. Zum Zeitpunkt $\nu$ gibt es $2^{\nu+1}$ solcher Knoten. Beispielsweise sind für $\nu = 3$ genau $2^4 = 16$ Knoten zu erkennen.

Die zu den Gesamtfehlergrößen $\gamma_{\nu}(i)$ gehörigen Amplitudenkoeffizienten ergeben sich, wenn man den Weg vom Anfangsknoten bis zum betrachteten Knoten verfolgt. Es wird vereinbart, dass einem nach oben gerichteten Zweig der Koeffizient $a_\nu=1$ und einem nach unten gerichteten Zweig der Koeffizient $a_\nu=0$ zugeordnet wird.

Beispielsweise kennzeichnet der grün hinterlegte Knoten $\gamma_{3}(\rm 1100)$ die Gesamtfehlergröße unter der hypothetischen Annahme, dass die Symbole $a_1=1$, $a_2=1$, $a_3=0$, $a_4=0$ gesendet wurden. Diese Zuordnung kann auch aus den Richtungen der Pfeile im Baumdiagramm abgelesen werden: Zunächst zweimal nach oben, dann zweimal nach unten.

Aufgrund des Vorläufers muss bereits zum Zeitpunkt $\nu = 3$ der Koeffizient $a_4$ mitberücksichtigt werden. Alle Knoten $\gamma_{\nu}(i)$, die unter der Voraussetzung $a_{\nu +1}=1$ berechnet werden, sind im Baumdiagramm durch Rechtecke dargestellt, während die Hypothese $a_{\nu +1}=0$ jeweils durch ein abgerundetes Rechteck symbolisiert ist, zum Beispiel $\gamma_{2}(\rm 110)$ oder $\gamma_{3}(\rm 1100)$.

Die Zweige im Baumdiagramm sind den Fehlergrößen $\varepsilon_{\nu}(i)$ zugeordnet. Beim vorausgesetzten Grundimpuls (nur $g_{0}$ und $g_{-1}$ sind ungleich Null) gibt es zu jedem Zeitpunkt mit Ausnahme des Startzustandes $(\nu = 0)$ genau vier unterschiedliche Größen:

$$\varepsilon_{\nu}(00) = |d_{\nu}|^2\hspace{0.05cm},\hspace{0.5cm}\varepsilon_{\nu}(01) = |d_{\nu}-g_{-1}|^2\hspace{0.05cm},\hspace{0.2cm} \varepsilon_{\nu}(10) = |d_{\nu}-g_{0}|^2\hspace{0.05cm},\hspace{0.2cm}\varepsilon_{\nu}(11) = |d_{\nu}-g_{0}-g_{-1}|^2\hspace{0.05cm}.$$

Die Gesamtfehlergröße $\gamma_{\nu}(i)$ ist gleich der Summe aus dem vorausgegangenen Knoten $\gamma_{\nu-1}(i\hspace{0.05cm}')$ und dem dazwischenliegenden Zweig $\varepsilon_{\nu}(i\hspace{0.05cm}'')$. Beispielsweise gilt für die hervorgehobenen Knoten:

$$\gamma_{1}(11)=\gamma_{0}(1)+\varepsilon_{1}(11) ,\hspace{0.25cm} \gamma_{2}(110)=\gamma_{1}(11)+\varepsilon_{2}(10) ,\hspace{0.25cm} \gamma_{3}(1100)=\gamma_{2}(110)+\varepsilon_{3}(00).$$

Bei den ersten Knoten $\gamma_{0}(0)$ und $\gamma_{0}(1)$ wird berücksichtigt, dass vor der eigentlichen Übertragung $(a_1$, $a_2$, ...$)$ vereinbarungsgemäß stets das Symbol $a_0 = 0$ übertragen wird. Daraus folgt:

$$\gamma_{0}(0)=\varepsilon_{0}(00)= |d_{0}|^2 \hspace{0.05cm},\hspace{0.2cm} \gamma_{0}(1)=\varepsilon_{0}(01)=|d_{0}-g_{-1}|^2 \hspace{0.05cm}.$$

Die beiden folgenden Beispiele werden hoffentlich diese etwas ermüdenden Aussagen verdeutlichen.

$\text{Beispiel 2:}$ Wir betrachten wie im $\text{Beispiel 1}$ die unipolare Quellensymbolfolge der Länge $N=3$ mit folgenden Parameterwerten:

$$g_{0}=0.7 \hspace{0.05cm},\hspace{0.2cm} g_{-1}=0.3 \hspace{0.05cm},\hspace{0.2cm} d_{0}=0.2 \hspace{0.05cm},\hspace{0.2cm} d_{1}=0.7 \hspace{0.05cm},\hspace{0.2cm} d_{2}=0.5 \hspace{0.05cm},\hspace{0.2cm} d_{3}=0 \hspace{0.05cm} \hspace{0.05cm}.$$

Dann gilt für die Fehlergrößen $\varepsilon_{\nu}(i)$ zu den Zeitpunkten $\nu = 0$ bis $\nu = 3$:

$$\nu = 0\text{:} \hspace{0.2cm}\varepsilon_{0}(00) = \big [0.2- (0 \cdot 0.7 + 0 \cdot 0.3) \big ]^2=0.04 \hspace{0.05cm},\hspace{0.4cm} \varepsilon_{0}(01) = \big [0.2- (0 \cdot 0.7 + 1 \cdot 0.3) \big ]^2=0.01 \hspace{0.05cm};$$

$$\nu = 1{:} \hspace{0.2cm}\varepsilon_{1}(00) = \big [0.7- (0 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.49 \hspace{0.05cm},\hspace{0.4cm} \varepsilon_{1}(01) = \big [0.7- (0 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.16 \hspace{0.05cm},$$

$$\hspace{1.4cm}\varepsilon_{1}(10) = \big [0.7- (1 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.00 \hspace{0.05cm}\hspace{0.4cm}\varepsilon_{1}(11) = \big [0.7- (1 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.09 \hspace{0.05cm};$$

$$\nu = 2\text{:} \hspace{0.2cm}\varepsilon_{2}(00) = \big [0.5- (0 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.25 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{2}(01) = \big [0.5- (0 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.04 \hspace{0.05cm},$$

$$\hspace{1.4cm}\varepsilon_{2}(10) = \big [0.5- (1 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.04 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{2}(11) = \big [0.5- (1 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.25 \hspace{0.05cm};$$

$$ \nu = 3\text{:} \hspace{0.2cm}\varepsilon_{3}(00) = \big [0.0- (0 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.00 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{3}(01) = \big [0.0- (0 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.09 \hspace{0.05cm},$$

$$\hspace{1.4cm}\varepsilon_{3}(10) = \big [0.0- (1 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.49 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{3}(11) = \big [0.0- (1 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=1.00 \hspace{0.05cm}.$$

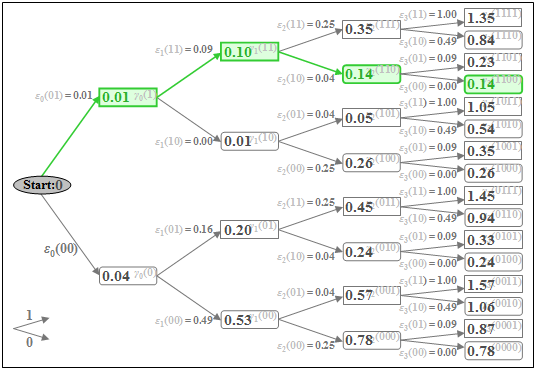
$\text{Beispiel 3:}$ Mit den im $\text{Beispiel 2}$ ermittelten Fehlergrößen $\varepsilon_{\nu}(i)$ können nun auch die Gesamtfehlergrößen $\gamma_{\nu}(i)$ berechnet werden. Nachfolgend ist das Baumdiagramm mit den Gesamtfehlergrößen $\gamma_{\nu}(i)$ als Knoten für die Zeitpunkte $\nu = 0$ bis $\nu = 3$ dargestellt.

Iterative Berechnung der Gesamtfehlergrößen (Beispiel)

Die minimale Gesamtfehlergröße zum Zeitpunkt $\nu = 3$ ist $\gamma_{3}(\rm 1100) = 0.14$. Daraus ergeben sich die Koeffizienten der nach den vorliegenden Signalwerten $d_0 = 0.2$, $d_1 = 0.7$, $d_2 = 0.5$ und $d_3 = 0$ mit größter Wahrscheinlichkeit gesendeten (unipolaren) Folge zu $a_1 = 1$, $a_2 = 1$ und $a_3 = 0$ (grüner Pfad).

Weiter ist anzumerken:

Ist die Folgenlänge $N = 3$ (das heißt: nur drei Symbole werden durch den Viterbi–Empfänger gemeinsam entschieden), so ist auch die Entscheidung $a_4 = 0$ mit Sicherheit die richtige, da alle Koeffizienten $a_{\nu>3}$ als Null vorausgesetzt wurden.

Bei längerer Folge $(N > 3)$ kann aber aus dem minimalen Wert $\gamma_{3}(\rm 1100)$ nicht unbedingt geschlossen werden, dass $a_1 = 1$, $a_2 = 1$, $a_3 = 0$ tatsächlich Teil der wahrscheinlichsten Folge ist. Bei Berücksichtigung weiterer Abtastwerte $(d_4$, $d_5$, ...$)$ könnte sich dieses vorläufige Ergebnis durchaus noch ändern.

Minimale Gesamtfehlergrößen

Vereinfachung des Baumdiagramms nach Viterbi

Wir gehen weiterhin von den Zahlenwerten der letzten Beispiele aus:

$$d_{0}=0.2 ,\hspace{0.1cm} d_{1}=0.7 ,\hspace{0.1cm} d_{2}=0.5 ,\hspace{0.1cm} d_{3}=0 ,$$

$$g_{0}=0.7 ,\hspace{0.1cm} g_{-1}=0.3 .$$

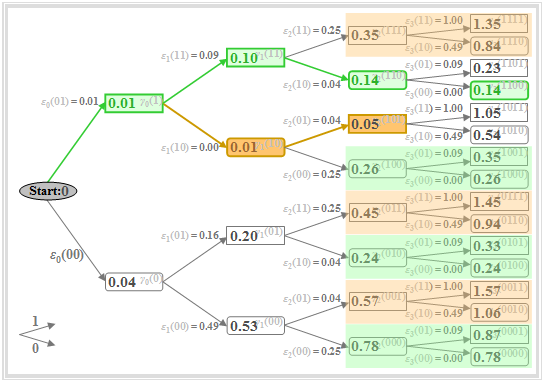
Damit ändert sich auch am Baumdiagramm gegenüber dem $\text{Beispiel 3}$ nichts. Durch einige farbliche Markierungen in dieser Grafik wird nur angedeutet, in welcher Weise das Baumdiagramm entsprechend den Vorschlägen von Viterbi vereinfacht werden kann.

Wichtige Eigenschaften des Viterbi–Entscheiders lassen sich in obiger Grafik beispielsweise zum Zeitpunkt $\nu = 2$ erkennen:

Zum Zeitpunkt $\nu = 2$ ist die minimale Gesamtfehlergröße $\gamma_{2}(\rm 101) = 0.05$ (braun hervorgehoben). Das bedeutet: Eine Entscheidung bei $\nu = 2$ – basierend auf $d_0$, $d_1$ und $d_2$ – wäre zugunsten der Folge $\rm 101$ anstelle der gesendeten Folge $\rm 110$ ausgegangen.

Daraus folgt: Eine zu frühe endgültige Festlegung sollte unbedingt vermieden werden. Allerdings kann man zu jedem Zeitpunkt $\nu$ bereits mehrere Teilsymbolfolgen ausschließen, die zu späteren Zeitpunkten nicht mehr berücksichtigt werden müssen.

Zu $\gamma_{2}(\rm 111) = 0.35$ werden die gleichen Fehlergrößen $\varepsilon_{3}(\rm 11)$ bzw. $\varepsilon_{3}(\rm 10)$ hinzuaddiert wie zu $\gamma_{2}(\rm 101) = 0.05$. Wegen $\gamma_{2}(\rm 111) > \gamma_{2}(\rm 101)$ steht somit bereits bei $\nu = 2$ fest, dass $\rm 111$ nicht Bestandteil der wahrscheinlichsten Folge sein kann. Gleiches gilt für $\rm 001$ und $\rm 011$. Diese Knoten und alle ihre Nachfahren müssen deshalb nicht weiter beachtet werden (braune Überdeckungen).

Auch die abgerundeten Knoten $\gamma_{2}(\rm 000) = 0.78$, $\gamma_{2}(\rm 010) = 0.24$ und $\gamma_{2}(\rm 100) = 0.26$ sind nicht Bestandteil der wahrscheinlichsten Folge, da sie größer sind als der grün markierte Knoten $\gamma_{2}(\rm 110) = 0.14$. Auch diese und ihre Nachfahren müssen ab dem Zeitpunkt $\nu = 3$ nicht mehr berücksichtigt werden (grüne Überdeckungen).

$\text{Fazit:}$

Von den acht Knoten bei $\nu = 2$ müssen nur zwei weiterverfolgt werden, nämlich das Rechteck $\gamma_{2}(\rm 101) = 0.05$ und das abgerundete Rechteck $\gamma_{2}(\rm 110) = 0.14$.
Diese beschreiben die minimalen Gesamtfehlergrößen unter der Annahme, dass $a_3 = 0$ bzw. $a_3 = 1$ wäre.

Darstellung der minimalen Gesamtfehlergrößen – Trellisdiagramm

Wir verallgemeinern nun das Ergebnis dieses Beispiels. Unter der weiterhin gültigen Annahme, dass der Grundimpuls neben dem Hauptwert $(g_0)$ nur einen Vorläufer $(g_{-1})$ aufweist, ergeben sich die beiden minimalen Gesamtfehlergrößen zum Zeitpunkt $\nu$ formal zu

$${\it \Gamma}_{\nu}(0) = {\rm Min}\left[{\it \Gamma}_{\nu-1}(0) + \varepsilon_{\nu}(00), \hspace{0.2cm}{\it \Gamma}_{\nu-1}(1) + \varepsilon_{\nu}(10)\right] \hspace{0.05cm},$$

$${\it \Gamma}_{\nu}(1) = {\rm Min}\left[{\it \Gamma}_{\nu-1}(0) + \varepsilon_{\nu}(01), \hspace{0.2cm}{\it \Gamma}_{\nu-1}(1) + \varepsilon_{\nu}(11)\right] \hspace{0.05cm}.$$

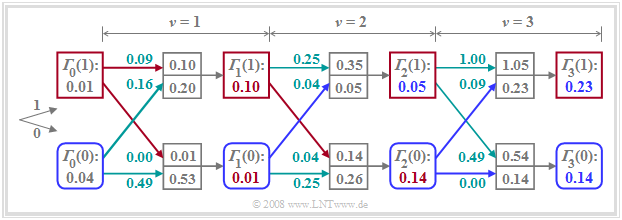
Das Verfahren der Gesamtfehlerminimierung lässt sich im Trellisdiagramm anschaulich darstellen.

Beispielhaftes Trellisdiagramm

Ein Vergleich mit den Bildern auf den letzten Seiten zeigt:

Der untere Zweig stellt die minimale Gesamtfehlergröße ${\it \Gamma}_{\nu}(0)$ dar, die zu jedem Zeitpunkt $\nu$ unter der Hypothese berechnet wird, dass $a_{\nu + 1} = 0$ gelten wird (blaue abgerundete Quadrate).

Dagegen beschreibt der obere Zweig die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\nu}(1)$ unter der Annahme $a_{\nu + 1} = 1$ (rote Quadrate). Auch hier sind die Zahlenwerte an das bisherige Beispiel angepasst.

Außer ${\it \Gamma}_{\nu}(0)$ und ${\it \Gamma}_{\nu}(1)$ muss der Maximum–Likelihood–Entscheider auch die dazugehörigen Symbolfolgen (Pfade) abspeichern. Diese Zweige sind in der Grafik rot bzw. blau hervorgehoben.

Falls ${\it \Gamma}_{\nu}$ aus dem Knoten ${\it \Gamma}_{\nu-1}(0)$ hervorgeht – also wenn der untere der beiden ankommenden Zweige hervorgehoben ist – so ist das dazugehörige Symbol $\rm 0$, andernfalls das Symbol $\rm 1$.

Zur Zeit $\nu = 3$ ergeben sich zum Beispiel sowohl ${\it \Gamma}_{3}(0) = 0.14$ als auch ${\it \Gamma}_{3}(1) = 0.23$ aus dem Vorgänger ${\it \Gamma}_{2}(0)$, so dass beide ausgewählte Pfade jeweils auf das Symbol $\rm 0$ verweisen (blaue Zweige).

Vereinfachtes Trellisdiagramm

Der Vorteil des Trellisdiagramms besteht darin, dass sich die Anzahl der Knoten und Zweige nicht bei jedem Iterationsschritt verdoppeln. Durch die Auswahl der minimalen Gesamtfehlergrößen werden nur noch diejenigen Symbolfolgen weiter betrachtet, die als Teil der wahrscheinlichsten Folge überhaupt noch in Frage kommen.

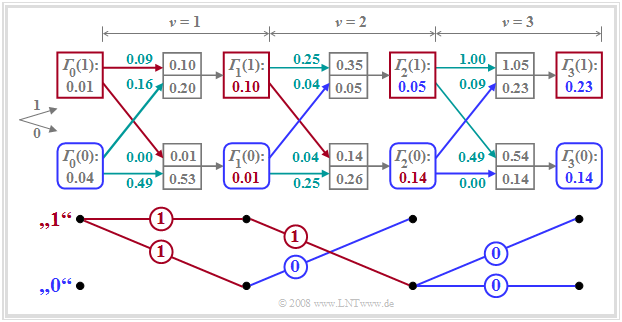
Das Trellisdiagramm lässt sich weiter vereinfachen, indem man nur noch die ausgewählten Zweige einzeichnet. Dies ist im unteren Teil der Grafik an unserem Zahlenbeispiel verdeutlicht. Zur Erinnerung: Die tatsächlich gesendeten Amplitudenkoeffizienten seien $a_1= 1$, $a_2= 1$ und $a_3= 0$, und das oben gezeichnete Trellisdiagramm wurde unter der Annahme berechnet, dass aufgrund der Impulswerte $g_{-1} = 0.3$ und $g_{0} = 0.7$ sowie des AWGN–Rauschens die Eingangswerte $d_0= 0.2$, $d_1= 0.7$, $d_2= 0.5$ und $d_3= 0$ am ML–Entscheider anliegen.

Trellisdiagramm und vereinfachtes Trellisdiagramm

Dieses vereinfachte Trellisdiagramm erlaubt folgende Aussagen:

Die Entscheidung über $a_1= 1$ kann sofort zum Zeitpunkt $\nu = 1$ getroffen werden, da sich unter beiden Hypothesen – nämlich das nachfolgende Symbol sei $a_2= 0$ bzw. dieses Symbol sei $a_2= 1$ – das gleiche Resultat $a_1= 1$ ergibt.

Dagegen kann zum Zeitpunkt $\nu = 2$ die endgültige Entscheidung über $a_2$ noch nicht getroffen werden. Unter der Annahme, dass $a_3= 0$ sein wird, müsste man sich für $a_2= 1$ entscheiden, während die Hypothese $a_3= 1$ zur Festlegung auf $a_2= 0$ führen würde.

Zur Zeit $\nu = 3$ ist die Entscheidung für $a_1= 1$, $a_2= 1$, $a_3= 0$ endgültig, da beide durchgehenden Pfade diese (die in diesem Fall richtige) Folge suggerieren.
Würde man die Entscheidung auf den Zeitpunkt $\nu = 4$ verschieben, so hätte man nicht mehr nutzbare Information über $a_1$, $a_2$ und $a_3$ zur Verfügung.

Alle Aussagen dieses Kapitels können mit dem interaktiven Applet Viterbi–Empfänger für einen Vorläufer verifiziert werden.

Erweiterung auf zwei Vorläufer

Wird der Grundimpuls durch die Abtastwerte $g_{0} \ne 0$, $g_{-1} \ne 0$ und $g_{-2} \ne 0$ beschrieben, so müssen im Trellisdiagramm zu jedem Zeitpunkt $\nu$ vier Metriken ${\it \Gamma}_{\nu}(00)$, ${\it \Gamma}_{\nu}(01)$, ${\it \Gamma}_{\nu}(10)$ und ${\it \Gamma}_{\nu}(11)$ bestimmt werden. ${\it \Gamma}_{\nu}(01)$ beschreibt dann beispielsweise die minimale Gesamtfehlergröße für die Detektion des Symbols $a_\nu$ unter der Hypothese, dass $a_{\nu-1} = 0$ und $a_{\nu-2} = 1$ sein werden, und es gilt:

$${\it \Gamma}_{\nu}(01) = {\rm Min}\big[{\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001), \hspace{0.2cm}{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101)\big] \hspace{0.05cm}.$$

In der Aufgabe 3.12 wird im Detail auf die Berechnung der Fehlergrößen (Metriken) und die Minimierung der Gesamtfehlergrößen (akkumulierten Metriken) eingegangen.

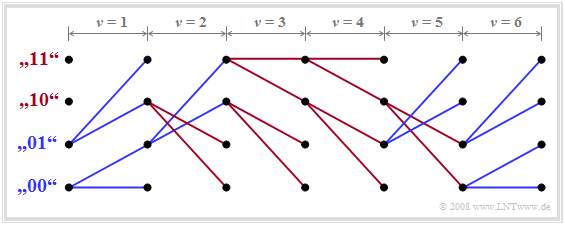
$\text{Beispiel 4:}$ Wir betrachten hier ein beispielhaftes Trellisdiagramm, das die (fehlerfreie) Detektion von folgender Symbolfolge widergibt:

$$a_{1}=0 \hspace{0.05cm},\hspace{0.2cm} a_{2}=0 \hspace{0.05cm},\hspace{0.2cm} a_{3}=1 \hspace{0.05cm},\hspace{0.2cm} a_{4}=1 \hspace{0.05cm},\hspace{0.2cm} a_{5}=1 \hspace{0.05cm},\hspace{0.2cm} a_{6}=0 \hspace{0.05cm}, \hspace{0.05cm}\text{...}$$

Trellisdiagramm für zwei Vorläufer

Dieses vereinfachte Trellisdiagramm erlaubt folgende Aussagen:

Alle von ${\it \Gamma}_{\nu}(00)$ bzw. ${\it \Gamma}_{\nu}(01)$ abgehende Zweige sind dem Symbol $\rm 0$ zugeordnet und blau gezeichnet. Die von den beiden oberen Zuständen abgehenden roten Zweige kennzeichnen das Symbol $\rm 1$.

Verfolgt man die durchgehenden Pfade, so erkennt man die angegebene Folge. Da zum Zeitpunkt $\nu = 6$ nur blaue Zweige ankommen, liegen hier die ersten sechs Bit der Folge endgültig fest.

Teilfolgen könnten aber auch bereits zu den Zeiten $\nu = 1$, $\nu = 3$ und $\nu = 4$ ausgegeben werden, da sich zu diesen Zeiten für alle vier Zustände die gleichen Teilpfade ergeben.

Dagegen darf bei $\nu = 2$ und $\nu = 5$ nicht sofort entschieden werden. Beispielsweise ist zum Zeitpunkt $\nu = 5$ nur sicher, dass entweder $a_5 = 0$ und $a_6 = 1$ sein werden oder $a_5 = 1$ und $a_6 = 0$. Andere Kombinationen sind nicht möglich.

Error probability in maximum likelihood decision

Die exakte Fehlerwahrscheinlichkeitsberechnung bei ML–Entscheidung (zum Beispiel mit dem Korrelations– oder dem Viterbi–Empfänger) ist sehr aufwändig. Dabei müssen

die Differenzenergien zwischen allen möglichen Symbolfolgen $Q_i$ und $Q_{j \ne i}$ ermittelt werden, wobei die Fehlerwahrscheinlichkeit im Wesentlichen durch die minimale Differenzenergie bestimmt wird;

auch die Einflüsse von Matched–Filter $H_{\rm MF}(f)$ und Dekorrelationsfilter $H_{\rm DF}(f)$ berücksichtigt und zusätzlich der Effektivwert $\sigma_d$ des Detektionsstörsignals bestimmt werden.

$\text{Ohne Beweis:}$ Eine einfache Näherung für die (mittlere) Fehlerwahrscheinlichkeit bei Maximum–Likelihood––Entscheidung lautet:

$$p_{\rm ML} = {\rm Q}\left(g_{\rm max}/{\sigma_d}\right) \hspace{0.3cm}{\rm mit}\hspace{0.2cm}g_{\rm max}= {\rm Max}\hspace{0.15cm} \vert g_\nu \vert \hspace{0.05cm}.$$

Die Näherung gilt nur für binäre bipolare Signalisierung. Bei unipolarer Signalisierung ist das Argument der Q-Funktion zu halbieren.

Für die folgende Interpretation und das anschließende Beispiel wird vorausgesetzt, dass $v + 1$ Grundimpulswerte (inklusive Hauptwert) von Null verschieden sind. Dann gilt:

Der Viterbi–Entscheider muss alle diese Grundimpulswerte berücksichtigen. Das bedeutet, dass ein Trellisdiagramm mit $2^v$ Zuständen zu bearbeiten ist.

Voraussetzung für die Gültigkeit obiger Gleichung ist die Unkorreliertheit der Störungen am Entscheider, die durch das Dekorrelationsfilter erreicht wird.

Für den Vergleich mit Schwellenwertentscheider $(p_{\rm SE})$ bzw. Entscheidungsrückkopplung $(p_{\rm DFE})$ wird der Störeffektivwert $\sigma_d$ als konstant vorausgesetzt.

Die Optimierung des ML–Systems führt zu sehr schmalbandigen Filtern, da alle Impulsausläufer durch den ML–Algorithmus herausgerechnet werden können.

Bei konstanter Rauschleistungsdichte $N_0$ (am Empfängereingang) ist somit der Störeffektivwert $\sigma_d$ (am Entscheider) beim ML–System kleiner als bei anderen Varianten.

Das bedeutet: Der Störabstandsgewinn durch die ML–Entscheidung ist unter Umständen noch größer, als es das folgende Beispiel $($mit $\sigma_d = \rm const.)$ ausdrückt.

$\text{Beispiel 5:}$ Wir betrachten die Grundimpulswerte $g_{0} = 0.6$ und $g_{-1} = g_{+1} = 0.2 \ ( = g_1)$. Zudem gehen wir vom konstanten Störeffektivwert $\sigma_d = 0.1$ aus. Zur Vereinfachung sind alle Größen normiert.

Bei einem Binärempfänger mit einfacher Schwellenwertentscheidung $\rm (SE)$ entsprechend dem Kapitel Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen ergibt sich bei bipolarer Signalisierung für die (mittlere) Fehlerwahrscheinlichkeit:

$$p_{\rm SE} = {1}/{4}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}+\hspace{-0.02cm}2 \cdot g_{1} }{\sigma_d}\right) +{1}/{2}\cdot {\rm Q}\left(\frac{g_{0} }{\sigma_d}\right)+ {1}/{4}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}2 \cdot g_{1} }{\sigma_d}\right) \approx {1}/{4}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}2 \cdot g_{1} }{\sigma_d}\right) = \frac{ {\rm Q}(2)}{4}= 0.57 \% \hspace{0.05cm}.$$

Für den Empfänger mit Entscheidungsrückkopplung $\rm (DFE)$ erhält man unter Berücksichtigung von $g_{+1} = 0$ (vollständige Kompensation des Nachläufers):

$$p_{\rm DFE} ={1}/{2}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}+\hspace{-0.02cm}g_{-1} }{\sigma_d}\right) +{1}/{2}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}g_{-1} }{\sigma_d}\right)\approx {1}/{2}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}g_{-1} }{\sigma_d}\right)=\frac{{\rm Q}(4)}{4}= 0.16 \cdot 10^{-4} \hspace{0.05cm}.$$

Dagegen führt die Anwendung der Maximum–Likelihood–Entscheidung (mit Korrelations–Empfänger bzw. Viterbi–Empfänger) $\rm (ML)$ zur sehr viel kleineren Fehlerwahrscheinlichkeit

$$p_{\rm ML} = {\rm Q}\left(\frac{g_{0}}{\sigma_d}\right) \approx {\rm Q}(6) = 10^{-9} \hspace{0.05cm}.$$

Dies entspricht gegenüber den beiden anderen Systemen einem Störabstandsgewinn von ca. $3 \ \rm dB$ (gegenüber $\rm DFE$) bzw. $7.5 \ \rm dB$ (gegenüber $\rm SE$). Das Ergebnis dieser einfachen Näherung wurde durch Simulationen im Wesentlichen bestätigt.

Um den beschriebenen Viterbi–Algorithmus direkt anwenden zu können, müssen in den Gleichungen die (normierten) Grundimpulswerte $g_{0} =0.2$, $g_{-1} =0.6$ und $g_{-2} =0.2$ eingestellt werden. Eine Zeitverschiebung um Vielfache der Symboldauer $T$ gegenüber dem aus Darstellungsgründen gewählten Koordinatensystem ändert nämlich die Leistungsmerkmale der Viterbi–Entscheidung nicht.

Die Maximum–Likelihood–Fehlerwahrscheinlichkeit nach obiger Gleichung richtet sich allein nach dem größten Grundimpulswert. Dabei kann es durchaus sein, dass ein "Vorläufer" $($hier: $g_{-1} =0.6)$ größer als der Hauptwert $g_{0}$ ist. Bei Schwellenwertentscheidung würde das zu einem geschlossenen Auge führen.

$\text{Fazit:}$ Eine Maximum–Likelihood–Entscheidung ist nur bei Vorhandensein von Impulsinterferenzen von Vorteil. Bei Nyquistentzerrung (das heißt: Nur der Grundimpulswert $g_0$ ist ungleich Null) arbeitet auch der Maximum–Likelihood–Empfänger symbolweise und mit gleicher Fehlerwahrscheinlichkeit ${\rm Q}(g_0/\sigma_d)$ wie ein Empfänger mit Schwellenwertentscheidung.