Contents
- 1 Improvements regarding speech coding
- 2 Application of the CDMA method to UMTS
- 3 Spreading codes and scrambling with UMTS
- 4 Channel coding for UMTS
- 5 Frequency responses and pulse shaping for UMTS
- 6 Modulationsverfahren bei UMTS
- 7 Single–User–Empfänger
- 8 Rake–Empfänger
- 9 Multi–User–Empfänger
- 10 Near–Far–Effekt
- 11 Träger–zu–Interferenz–Leistungsverhältnis (CIR)
- 12 Power and power control in UMTS
- 13 Link–Budget
- 14 UMTS–Funkressourcenverwaltung
- 15 Aufgaben zum Kapitel
- 16 Quellenverzeichnis
Improvements regarding speech coding
In the chapter "Global System for Mobile Communications" $\rm (GSM)$ of this book, several speech codecs have already been described in detail.
$\text{Reminder:}$ A speech codec is used to reduce the data rate of a digitized speech or music signal.
- In the process, redundancy and irrelevance are removed from the original signal.
- The artificial word "codec" indicates that the same functional unit is used for both, encoding and decoding.
Among others, the "Adaptive Multi-Rate Codec" $\rm (AMR)$ based on $\rm ACELP$ $($"Algebraic Code Excited Linear Prediction"$)$ was introduced,
- which in the frequency range from $\text{300 Hz}$ to $\text{3400 Hz}$
- dynamically switches between eight different modes $($single codecs$)$
- of different data rate in the range of $\text{4. 75 kbit/s}$ to $\text{12.2 kbit/s}$.
These codecs are also supported in UMTS Release 99 and Release 4. Compared to the earlier speech codecs $($Full Rate, Half Rate, Enhanced Full Rate Vocoder$)$, they allow
- independence from channel conditions and network load,
- the ability to adapt data rates to conditions,
- improved flexible error protection in the event of more severe radio interference, and
- thereby providing better overall voice quality.
In 2001, the "3rd Generation Partnership Project" $\text{(3gpp)}$ and the "International Telecommuncation Union" $\text{(ITU)}$ specified the new voice codec »Wideband AMR« for UMTS Release 5. This is a further development of AMR and offers
- an extended bandwidth from $\text{50 Hz}$ to $\text{7 kHz}$
$($sampling frequency $\text{16 kHz})$,
- a total of nine modes between $\text{6.6 kbit/s}$ and $\text{23.85 kbit/s}$
$($of which only five modes are used$)$, and
- improved voice quality and better (more natural) sound.
$\text{Some features of wideband AMR}$
- Speech data is delivered to the codec as PCM encoded speech with $16\hspace{0.05cm}000$ samples per second.
- The speech coding is done in blocks of $\text{20 ms}$ and the data rate is adjusted every $\text{20 ms}$.
- The band $\text{(50 Hz}$ to $\text{7000 Hz})$ is divided into two sub-bands, which are encoded differently to allocate more bits to the subjectively important frequencies.
- The upper band $\text{(6400 Hz}$ to $\text{7000 Hz})$ is transmitted only in the highest mode $($with $\text{23.85 kbit/s)}$ .
- In all other modes, only frequencies $\text{50 Hz}$ to $\text{6400 Hz}$ are considered in encoding.
- Wideband AMR supports "discontinuous transmission"' $\rm (DTX)$. This feature means that transmission is paused during voice pauses, reducing both mobile station power consumption and overall interference at the air interface. This process is also known as "Source-Controlled Rate" $\rm (SCR)$.
- The "Voice Activity Detection" $\rm (VAD)$ determines whether speech is in progress or not and inserts a "silence descriptor frame" during speech pauses.
- The subscriber is suggested the feeling of a continuous connection by the decoder inserting synthetically generated "comfort noise" during speech pauses.
Application of the CDMA method to UMTS
UMTS uses the multiple access method "Direct Sequence Code Division Multiple Access" $\rm (DS-CDMA)$, which has already been discussed in the "PN modulation" chapter of the book "Modulation Methods".
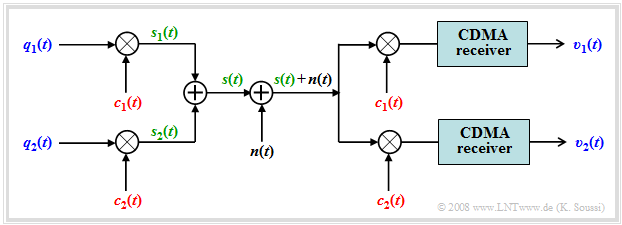
Here follows a brief summary of this method according to the diagram describing such a system in the equivalent low-pass range and highly simplified:
- The two data signals $q_1(t)$ and $q_2(t)$ are supposed to use the same channel without interfering with each other. The bit duration of each is $T_{\rm B}$.
- Each of the data signals is multiplied by an associated spreading code $c_1(t)$ resp. $c_2(t)$.
- The sum signal $s(t) = q_1(t) · c_1(t) + q_2(t) · c_2(t)$ is formed and transmitted.
- At the receiver, the same spreading codes $c_1(t)$ resp. $c_2(t)$ are added, thus separating the signals again.
- Assuming orthogonal spreading codes and a small AWGN noise, the two reconstructed signals at the receiver output are:
- $$v_1(t) = q_1(t) \ \text{and} \ v_2(t) = q_2(t).$$
- For AWGN noise signal $n(t)$ and orthogonal spreading codes, this does not change the error probability due to other participants.
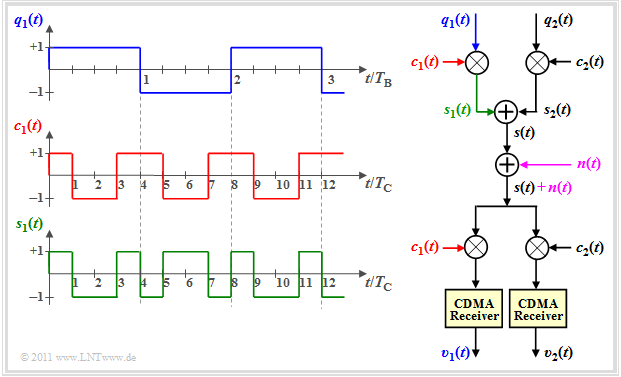
$\text{Example1:}$ The upper graph shows three data bits $(+1, -1, +1)$ of the rectangular signal $q_1(t)$ from subscriber 1, each with symbol duration $T_{\rm B}$.
- Here, the symbol duration $T_{\rm C}$ of the spreading code $c_1(t)$ ⇒ also called "chip duration" is smaller by a factor $4$.
- The multiplication $s_1(t) = q_1(t) · c_1(t)$ results in a chip sequence of length $12 · T_{\rm C}$.
One recognizes from this sketch that the signal $s_1(t)$ is of higher frequency than $q_1(t)$.
- This is why this modulation method is often also called "spread spectrum".
- The CDMA receiver reverses this "band spreading". We refer to this "receiver-side band spreading" as "band compression".
$\text{Summarizing:}$ By applying "Direct Sequence Code Division Multiple Access" $\rm (DS-CDMA)$ to a data bit sequence $q(t)$
- increases the bandwidth of $s(t) = q(t) \cdot c(t)$ by the »spreading factor« $J = T_{\rm B}/T_{\rm C}$ – this is equal to the number of "chips per bit";
- the chip rate $R_{\rm C}$ is greater than the bit rate $R_{\rm B}$ by a factor $J$;
- the bandwidth of the entire CDMA signal is greater than the bandwidth of each user by a factor $J$.
That is: $\text{In UMTS, the entire bandwidth is available to each subscriber for the entire transmission duration}$.
Recall: In GSM, both "Frequency Division Multiple Access" and "Time Division Multiple Access" are used as multiple access methods.
- Here, each subscriber has only a limited frequency band $\rm (FDMA)$, and
- he only has access to the channel within time slots $\rm (TDMA)$.
Spreading codes and scrambling with UMTS
The spreading codes for UMTS should
- be orthogonal to each other to avoid mutual interference between subscribers,
- allow a flexible realization of different spreading factors $J$.
⇒ The issue presented here is also illustrated by the German-language SWF applet "OVSF codes".
$\text{Example 2:}$ An example of this is the »orthogonal variable spreading factor« $\rm (OVSF)$, which provide codes of lengths from $J = 4$ to $J = 512$.
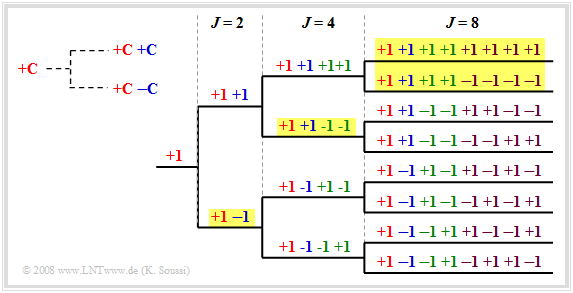
These can be created using a code tree, as shown in the diagram. Here, at each branch, two new codes are created from one code $C$:
- $(+C \ +\hspace{-0.1cm}C)$, and
- $(+C \ -\hspace{-0.1cm}C)$.
Note that no predecessor and successor of a code may be used.
- So in the drawn example, eight spreading codes with spreading factor $J = 8$ could be used.
- Also possible are the four codes with yellow background
- once with $J = 2$,
- once with $J = 4$, and
- twice with $J = 8$.
But the lower four codes with spreading factor $J = 8$ cannot be used, because they all start with "$+1 \ -\hspace{-0.1cm}1$", which is already occupied by the OVSF code with spreading factor $J = 2$.
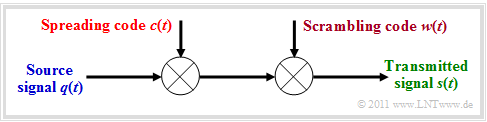
To obtain more spreading codes and thus be able to supply more participants, after the band spreading with $c(t)$
- the sequence is chip-wise scrambled again with $w(t)$,
- without any further spreading.
The »scrambling code« $w(t)$ has same length and rate as the spreading code $c(t)$.
⇒ Scrambling causes the codes to lose their complete orthogonality; they are called "quasi-orthogonal".
- For these codes, although the "cross-correlation function" $\rm (CCF)$ between different spreading codes is non-zero.
- But they are characterized by a pronounced "auto-correlation function" $\rm (ACF)$ around zero, which facilitates detection at the receiver.
- Using quasi-orthogonal codes makes sense because the set of orthogonal codes is limited and scrambling allows also different userts to use the same spreading codes.
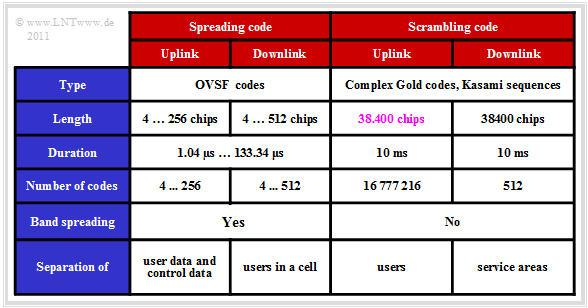
The table summarizes some data of spreading and scrambling codes.
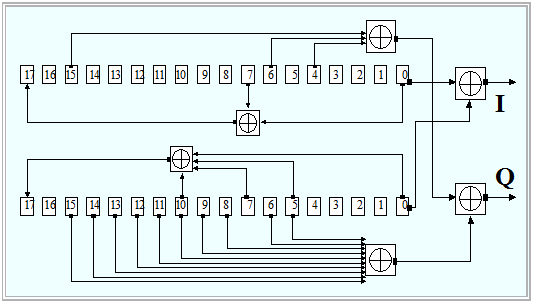
$\text{Example 3:}$ In UMTS, so-called »Gold codes« are used for scrambling. The graphic from [3gpp][1] shows the block diagram for the circuitry generation of such codes.
- Two different pseudonoise sequences of equal length $($here: $N = 18)$ are first generated in parallel using shift registers and added bitwise using "exclusive-or" gates.
- In the uplink, each mobile station has its own scrambling code and the separation of each channel is done using the same code.
- In contrast, in the downlink, each coverage area of a "Node B" has a common scrambling code
.
Channel coding for UMTS
With UMTS, the EFR- and AMR-encoded voice data pass through a two-stage error protection $($similar to GSM$)$, consisting of
- formation of "cyclic redundancy check bits" $\rm (CRC)$,
- subsequent convolutional encoding.
However, these methods differ from those used for GSM in that they are more flexible, since for UMTS they have to take different data rates into account.
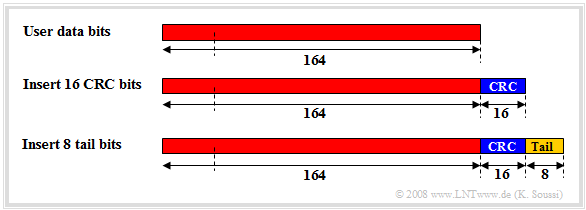
⇒ For »error detection«, eight, twelve, sixteen or $24$ CRC bits are formed depending on the size of the transport block $\text{(10 ms}$ or $\text{20 ms})$, and appended to it.
- Eight tail bits are also inserted at the end of each frame for synchronization purposes.
- The diagram shows a transport block of the DCH channel with $164$ user data bits, to which $16$ CRC bits and eight tail bits are appended.
⇒ For »error correction«, UMTS uses two different methods, depending on the data rate:
- For low data rates, "convolutional codes" with code rates $R = 1/2$ or $R = 1/3$ are used as with GSM. These are generated with eight memory elements of a feedback shift register $(256$ states$)$. The coding gain is approximately $4.5$ to $6$ dB with code rate $R = 1/3$ and at low error rates.
- For higher data rates, one uses "turbo codes" of rate $R = 1/3$. The shift register consists here of three memory cells, which can assume a total of eight states. The gain of turbo codes is larger by $2$ to $3$ dB than by convolutional codes and depends on the number of iterations. You need a processor with high processing power for this and there may be relatively large delays.
After channel coding, the data is fed to an "interleaver" as in GSM, in order to be able to resolve bundle errors caused by fading on the receiving side. Finally, for "rate matching" of the resulting data to the physical channel, individual bits are removed $($"puncturing"$)$ or repeated $($"repetition"$)$ according to a predetermined algorithm.
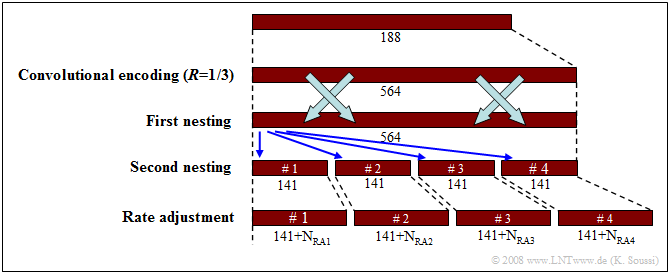
$\text{Example 4:}$ The graph first shows the increase in bits due to a convolutional or turbo code of rate $R =1/3$, where the $188$ bit time frame $($after the CRC checksum and tail bits$)$ becomes a $564$ bit frame.
- Followed by a first $($external$)$ nesting and then a second $($internal$)$ nesting.
- After this, the time frame is divided into four subframes of $141$ bits each, and these are then matched to the physical channel by rate matching.
Frequency responses and pulse shaping for UMTS
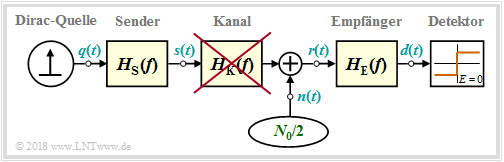
In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems bei idealem Kanal aus ⇒ $H_{\rm K}(f) = 1$.
Insbesondere gelte:
- Das Sendeimpulsfilter wandelt die binären $\{0, \ 1\}$ Daten in physikalische Signale. Das Filter wird beschrieben durch den Frequenzgang $H_{\rm S}(f)$, der formgleich mit dem Spektrum eines einzelnen Sendeimpulses ist.
- Bei UMTS ist das Empfangsfilter $H_{\rm E}f) = H_{\rm S}(f)$ an den Sender angepasst (Matched–Filter) und der Gesamtfrequenzgang $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$ erfüllt das erste Nyquistkriterium:
- $$ H(f) = H_{\rm CRO}(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \cos^2 \left( \frac {\pi \cdot (|f| - f_1)}{2 \cdot (f_2 - f_1)} \right)\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm sonst }\hspace{0.05cm}. \end{array} \begin{array}{*{20}c} |f| \le f_1, \\ |f| \ge f_2,\\ \\\end{array}$$
Das bedeutet: Zeitlich aufeinander folgende Impulse stören sich nicht gegenseitig ⇒ es treten keine Impulsinterferenzen (englisch: Intersymbol Interference, ISI) auf. Die zugehörige Zeitfunktion lautet:
- $$h(t) = h_{\rm CRO}(t) ={\rm si}(\pi \cdot t/ T_{\rm C}) \cdot \frac{\cos(r \cdot \pi t/T_{\rm C})}{1- (2r \cdot t/T_{\rm C})^2}. $$
- „CRO” steht hierbei für Cosinus–Rolloff (englisch: Raised Cosine).
- Die Summe $f_1 + f_2$ ist gleich dem Kehrwert der Chipdauer $T_{\rm C} = 260 \ \rm ns$, also gleich $3.84 \ \rm MHz$.
- Der Rolloff–Faktor (wir bleiben bei der in $\rm LNTwww$ gewählten Bezeichnung $r$, im UMTS–Standard wird hierfür $\alpha$ verwendet)
- $$r = \frac{f_2 - f_1}{f_2 + f_1} $$
- wurde bei UMTS zu $r = 0.22$ festgelegt. Die beiden Eckfrequenzen sind somit
- $$f_1 = {1}/(2 T_{\rm C}) \cdot (1-r) \approx 1.5\,{\rm MHz}, \hspace{0.2cm} f_2 ={1}/(2 T_{\rm C}) \cdot (1+r) \approx 2.35\,{\rm MHz}.$$
- Die erforderliche Bandbreite beträgt $B = 2 · f_2 = 4.7 \ \rm MHz$. Für jeden UMTS–Kanal steht somit mit $5 \ \rm MHz$ ausreichend Bandbreite zur Verfügung.
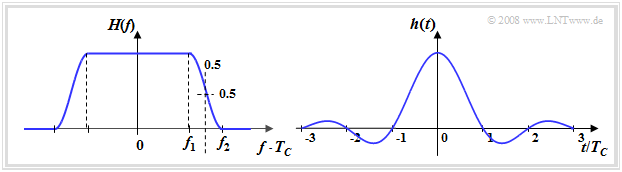
$\text{Fazit:}$ Die Grafik zeigt
- links das (normierte) Nyquistspektrum $H(f)$, und
- rechts den zugehörigen Nyquistimpuls $h(t)$, dessen Nulldurchgänge im Abstand $T_{\rm C}$ äquidistant sind.
$\text{Es ist zu beachten:}$
- Das Sendefilter $H_{\rm S}(f)$ und das Matched–Filter $H_{\rm E}(f)$ sind jeweils Wurzel–Cosinus–Rolloff–förmig (englisch: Root Raised Cosine). Erst das Produkt $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$ führt zum Cosinus–Rolloff.
- Das bedeutet auch: Die Impulsantworten $h_{\rm S}(t)$ und $h_{\rm E}(t)$ erfüllen für sich allein die erste Nyquistbedingung nicht. Erst die Kombination aus beiden (im Zeitbereich die Faltung) führt zu den gewünschten äquidistanten Nulldurchgängen.
Modulationsverfahren bei UMTS
Die bei UMTS eingesetzten Modulationsverfahren können wie folgt zusammengefasst werden:
- In der Abwärtsrichtung (Downlink) wird zur Modulation Quaternary Phase Shift Keying (QPSK) verwendet – sowohl bei FDD als auch bei TDD. Dabei werden Nutzdaten (DPDCH–Kanal) und Kontrolldaten (DPCCH–Kanal) zeitlich gemultiplext.
- Bei TDD wird das Signal in Aufwärtsrichtung (Uplink) ebenfalls mittels QPSK moduliert, nicht aber bei FDD. Hier wird vielmehr eine zweifache binäre PSK (englisch: Dual Channel–BPSK) verwendet.
Bei Dual–Channel BPSK wird zwar ebenfalls der QPSK–Signalraum genutzt, aber in Inphase– und Quadratur–Komponente werden unterschiedliche Kanäle übertragen. Pro Modulationsschritt werden also zwei Chips übertragen. Die Brutto–Chiprate ist daher doppelt so groß wie die Modulationsrate von $3.84$ Mchip pro Sekunde.
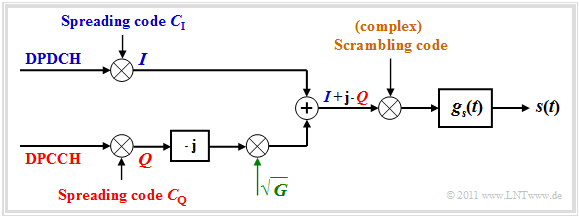
$\text{Beispiel 5:}$ Die Grafik zeigt dieses I/Q–Multiplexing–Verfahren, wie es auch bezeichnet wird, im äquivalenten Tiefpassbereich:
- Die gespreizten Nutzdaten des DPDCH–Kanals werden auf die Inphase–Komponente und die gespreizten Kontrolldaten des DPCCH–Kanals auf die Quadratur–Komponente moduliert und übertragen.
- Nach der Modulation wird die Quadratur–Komponente mit der Wurzel des Leistungsverhältnisses $G$ zwischen den beiden Kanälen gewichtet, um den Einfluss des Leistungsunterschieds zwischen $I$ und $Q$ zu minimieren.
- Abschließend wird das komplexe Summensignal $(I +{\rm j} · Q)$ mit einem ebenfalls komplexen Verwürfelungscode multipliziert.
$\text{Fazit:}$ Ein Vorteil der zweifachen BPSK–Modulation ist die Möglichkeit der Verwendung stromsparender Verstärker.
- Zeitmultiplex von Nutz– und Kontrolldaten wie im Uplink ist aber im Downlink nicht möglich.
- Ein Grund hierfür ist der Einsatz von Discontinuous Transmission (DTX) und die damit verbundenen zeitlichen Einschränkungen.
Single–User–Empfänger
Aufgabe eines CDMA–Empfängers ist es, aus der Summe der gespreizten Datenströme die gesendeten Daten der einzelnen Teilnehmer zu separieren und zu rekonstruieren. Dabei unterscheidet man zwischen Single–User–Empfängern und Multi–User–Empfängern.
Im Downlink von UMTS wird stets ein Single–User–Empfänger verwendet, da in der Mobilstation eine gemeinsame Detektion aller Teilnehmer wegen der Vielzahl aktiver Teilnehmer sowie der Länge der Verwürfelungscodes und des asynchronen Betriebs zu aufwändig wäre.
Ein solcher Empfänger besteht aus einer Bank unabhängiger Korrelatoren. Jeder einzelne der insgesamt $J$ Korrelatoren gehört zu einer spezifischen Spreizfolge. Die Korrelation wird meist in einer so genannten Korrelatordatenbank softwaremäßig gebildet.
Dabei erhält man am Korrelatorausgang die Summe aus
- der Autokorrelationsfunktion des Spreizcodes und
- der Kreuzkorrelationsfunktion aller anderen Teilnehmer mit dem teilnehmereigenen Spreizcode.
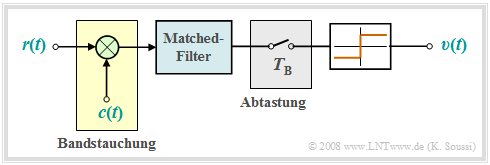
Die Grafik zeigt die einfachste Realisierung eines solchen Empfängers mit Matched–Filter.
- Das Empfangssignal $r(t)$ wird zunächst mit dem Spreizcode $c(t)$ des betrachteten Teilnehmers multipliziert, was als Bandstauchung oder Entspreizung bezeichnet wird (gelbe Hinterlegung).
- Danach folgt die Faltung mit der Impulsantwort des Matched–Filters (Root Raised Cosine), um das SNR zu maximieren, und die Abtastung im Bittakt ( $T_{\rm B}$ ).
- Abschließend erfolgt die Schwellenwertentscheidung, die das Sinkensignal $v(t)$ und damit die Datenbit des betrachteten Teilnehmers liefert.
$\text{Bitte beachten Sie:}$
Beim AWGN–Kanal haben die Bandspreizung beim Sender und die daran angepasste Bandstauchung beim Empfänger wegen $c(t)^2 = 1$ keinen Einfluss auf die Bitfehlerwahrscheinlichkeit. Wie in Aufgabe 4.5 gezeigt wird, gilt auch mit Bandspreizung/Bandstauchung bei optimalem Empfänger unabhängig vom Spreizgrad $J$:
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B} }/{N_{\rm 0} } } \hspace{0.05cm} \right )\hspace{0.05cm}. $$
Dieses Ergebnis lässt sich wie folgt begründen:
Die statistischen Eigenschaften von weißem Rauschen $n(t)$ werden durch die Multiplikation mit dem $±1$–Signal $c(t)$ nicht verändert.
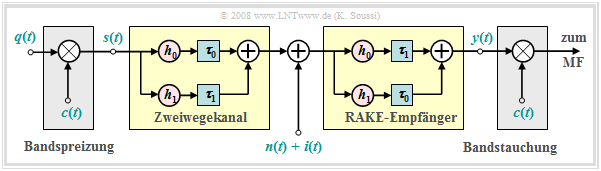
Rake–Empfänger
Ein weiterer Empfänger für die Single–User–Detektion ist der Rake–Empfänger, der bei einem Mehrwegekanal zu deutlichen Verbesserungen führt. Die Grafik zeigt seinen Aufbau für einen Zweiwegekanal mit
- einem direkten Pfad mit Koeffizient $h_0$ und Verzögerungszeit $τ_0$,
- einem Echo mit Koeffizient $h_1$ und Verzögerungszeit $τ_1$.
Zur Vereinfachung werden hier die Koeffizienten $h_0$ und $h_1$ als reell angenommen. Aufgrund der Darstellung im äquivalenten Tiefpassbereich könnten diese auch komplex sein.
Aufgabe des Rake–Empfängers ist es, die Signalenergien aller Pfade (in diesem Beispiel nur zwei) auf einen einzigen Zeitpunkt zu konzentrieren. Er arbeitet demnach wie eine Harke für den Garten, was auch die deutsche Übersetzung für „Rake” ist.
Legt man einen Diracimpuls zur Zeit $t = 0$ an den Kanaleingang an, so gibt es am Ausgang des Rake–Empfängers drei Diracimpulse:
- $$ s(t) = \delta(t) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} y(t) = h_0 \cdot h_1 \cdot \delta(t - 2\tau_0) + (h_0^2 + h_1^2) \cdot \delta(t - \tau_0 - \tau_1)+ h_0 \cdot h_1 \cdot \delta(t - 2\tau_1) .$$
- Die Signalenenergie konzentriert sich auf den Zeitpunkt $τ_0 + τ_1$. Von den insgesamt vier Wegen tragen zwei dazu bei (mittlerer Term).
- Die Diracfunktionen bei $2τ_0$ und $2τ_1$ bewirken zwar Impulsinterferenzen. Ihre Gewichte sind aber deutlich kleiner als die des Hauptpfades.
$\text{Beispiel 6:}$ Mit den Kanalparametern $h_0 = 0.8$ und $h_1 = 0.6$ beinhaltet der Hauptpfad $($mit Gewicht $h_0)$ nur $0.82/(0.82 + 0.62) = 64\%$ der gesamten Signalenergie. Mit Rake–Empfänger und den gleichen Gewichten lautet die obige Gleichung:
- $$ y(t) = 0.48 \cdot \delta(t - 2\tau_0) + 1.0 \cdot \delta(t - \tau_0 - \tau_1)+ 0.48 \cdot \delta(t - 2\tau_1) .$$
Der Anteil des Hauptpfades an der Gesamtenergie beträgt nun ${1^2}/{(1^2 + 0.48^2 + 0.48^2)} ≈ 68\%.$
Rake–Empfänger werden zur Implementierung in mobilen Geräten bevorzugt, sind aber bei vielen aktiven Teilnehmern nur begrenzt leistungsfähig. Bei einem Mehrwegekanal mit vielen $(M)$ Pfaden hat auch der Rake $M$ Finger. Der Hauptfinger (Main Finger) – auch Searcher genannt – ist dafür verantwortlich, die individuellen Pfade der Mehrfachausbreitung zu identifizieren und einzuordnen. Er sucht die stärksten Pfade und weist diese zusammen mit ihren Steuerinformationen anderen Fingern zu. Dabei wird die Zeit– und Frequenzsynchronisation aller Finger kontinuierlich mit den Kontrolldaten des empfangenen Signals verglichen.
Multi–User–Empfänger
Bei einem Single–User–Empfänger wird nur das Datensignal eines Teilnehmers entschieden, während alle anderen Teilnehmersignale als zusätzliches Rauschen betrachtet werden. Die Fehlerrate eines solchen Detektors wird jedoch dann sehr groß sein, wenn große Intrazellinterferenzen (viele aktive Teilnehmer in der betrachteten Funkzelle) oder Interzellinterferenzen (stark störende Teilnehmer in Nachbarzellen) vorliegen.
Dagegen treffen Multi–User–Empfänger (Mehrbenutzerempfänger) eine gemeinsame Entscheidung für alle aktiven Teilnehmer. Deren Eigenschaften können wie folgt zusammengefasst werden:
- Ein Multi–User–Empfänger betrachtet die Interferenzen anderer Teilnehmer nicht als Rauschen, sondern nutzt auch die in den Interferenzsignalen enthaltenen Informationen zur Detektion.
- Der Empfänger ist aufwändig zu realisieren und die Algorithmen sind äußerst rechenintensiv. Er beinhaltet eine extrem große Korrelatordatenbank gefolgt von einem gemeinsamen Detektor.
- Dem Multi–User–Empfänger müssen die Spreizcodes aller aktiven Teilnehmer bekannt sein. Diese Voraussetzung schließt einen Einsatz im UMTS–Downlink (also bei der Mobilstation) aus. Dagegen sind den Basisstationen alle teilnehmerspezifischen Spreizcodes a priori bekannt, so dass im Uplink die Mehrbenutzerdetektion auch tatsächlich zur Anwendung kommt.
- Manche Detektionsalgorithmen verlangen zusätzlich die Kenntnis anderer Signalparameter wie Energien und Verzögerungszeiten. Der gemeinsame Detektor – das Herzstück des Empfängers – ist dafür verantwortlich, den jeweiligen passenden Detektionsalgorithmus anzuwenden. Beispiele für die Mehrbenutzerdetektion sind Decorrelating Detection und Interference Cancellation.
Near–Far–Effekt
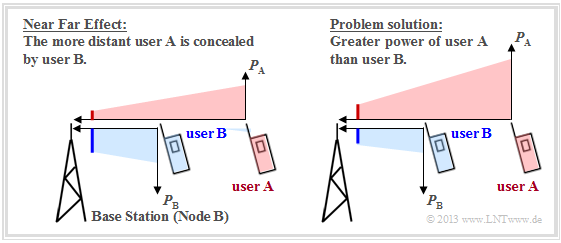
Der Near–Far–Effekt ist ausschließlich ein Problem des Uplinks, also der Übertragung von mobilen Teilnehmern zu einer Basisstation. Wir betrachten ein Szenario mit zwei unterschiedlich weit von der Basisstation entfernten Nutzern entsprechend folgender Grafik. Diese kann man wie folgt interpretieren:
- Senden beide Mobilstationen mit gleicher Leistung, so ist die Empfangsleistung des roten Nutzers $\rm A$ an der Basisstation aufgrund des Pfadverlustes deutlich kleiner als die des blauen Nutzers $\rm B$ (linkes Szenario). In großen Makrozellen kann der Unterschied bis zu $100 \ \rm dB$ ausmachen. Dadurch wird das rote Signal weitgehend durch das blaue verdeckt.
- Man kann den Near–Far–Effekt weitgehend vermeiden, wenn der weiter entfernte Nutzer $\rm A$ mit höherer Leistung sendet als Nutzer $\rm B$, wie im rechten Szenario angedeutet. An der Basisstation ist dann die Empfangsleistung beider Mobilstationen (nahezu) gleich.
Anmerkung: Bei einem idealisierten System (Einwegekanal, ideale A/D–Wandler, vollständig lineare Verstärker ) sind die übertragenen Daten der Nutzer orthogonal zueinander und man könnte die Nutzer auch bei sehr unterschiedlichen Empfangsleistungen einzeln detektieren. Diese Aussage gilt für UMTS (Mehrfachzugriffsverfahren: CDMA) ebenso wie für für das 2G–System GSM (FDMA/TDMA) und für das 4G–System LTE (TDMA/OFDMA).
In der Realität ist jedoch die Orthogonalität aufgrund folgender Ursachen nicht immer gegeben:
- verschiedene Empfangspfade ⇒ Mehrwegekanal,
- nicht ideale Eigenschaften der Spreiz– und Scramblingcodes bei CDMA,
- Asynchronität der Nutzer im Zeitbereich (Grundlaufzeit der Pfade),
- Asynchronität der Nutzer im Frequenzbereich (nicht ideale Oszillatoren und Dopplerverschiebung aufgrund der Mobilität der Nutzer).
Folglich sind die Nutzer nicht mehr orthogonal zueinander und der Störabstand des zu detektierenden Nutzers gegenüber den anderen Teilnehmern ist nicht beliebig hoch. Bei GSM und LTE kann man von Störabständen von $25 \ \rm dB$ und mehr ausgehen, bei UMTS (CDMA) jedoch nur von ca. $15 \ \rm dB$, bei hochratiger Datenübertragung eher noch von etwas weniger.
Träger–zu–Interferenz–Leistungsverhältnis (CIR)
Unter Kapazität wird allgemein die Anzahl der verfügbaren Übertragungskanäle pro Zelle verstanden werden. Da aber bei UMTS die Teilnehmerzahl im Gegensatz zum GSM nicht streng begrenzt ist, lässt sich hier keine feste Kapazität angeben.
- Bei perfekten Codes stören sich die Teilnehmer gegenseitig nicht. Dadurch wird die maximale Nutzerzahl allein durch den Spreizfaktor $J$ und die verfügbare Anzahl der zueinander orthogonalen Codes bestimmt, die aber ebenfalls limitiert ist.
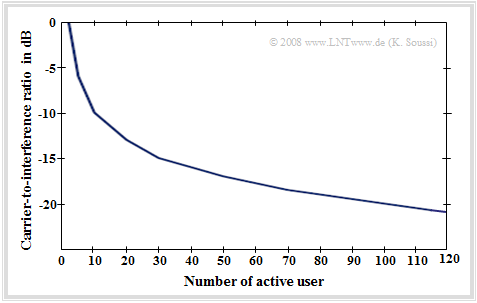
- Praxisnäher sind nichtperfekte, nur quasi–orthogonale Codes. Hier wird die „Kapazität” einer Funkzelle vorwiegend durch die entstehenden Interferenzen bzw. das Träger–zu–Interferenz–Leistungsverhältnis (englisch: Carrier–to–Interference Ratio, CIR) bestimmt.
Wie aus dieser Grafik zu ersehen ist, hängt das "CIR" direkt von der Anzahl aktiver Teilnehmer ab. Je mehr Teilnehmer aktiv sind, desto mehr Interferenzleistung entsteht und desto kleiner wird das "CIR".
Desweiteren hängt dieses für UMTS entscheidende Kriterium auch von folgenden Größen ab:
- der Topologie und dem Nutzerverhalten (aufgerufene Dienste),
- dem Spreizfaktor $J$ und der Orthogonalität des verwendeten Spreizcodes.
Um den störenden Einfluss der Interferenzleistung auf die Übertragungsqualität zu begrenzen, gibt es zwei Möglichkriten:
- Zellatmung: Nimmt bei UMTS die Anzahl der aktiven Teilnehmer signifikant zu, so wird der Zellenradius verkleinert und (wegen der nun weniger Teilnehmer in der Zelle) auch die aktuelle Interferenzleistung geringer. Für die Versorgung der Teilnehmer am Rande der verkleinerten Zelle springt dann eine weniger belastete Nachbarzelle ein.
- Leistungsregelung: Überschreitet die Gesamtinterferenzleistung innerhalb einer Funkzelle einen vorgegebenen Grenzwert, so wird die Sendeleistung aller Teilnehmer entsprechend herabgesetzt und/oder die Datenrate reduziert, was eine schlechtere Übertragungsqualität für alle zur Folge hat. Hierzu mehr auf der nächsten Seite.
Power and power control in UMTS
Als Regelgröße bei der Leistungsregelung in UMTS wird das Verhältnis zwischen der Signalleistung und der Interferenzleistung verwendet. Dabei gibt es Unterschiede zwischen dem FDD– und TDD–Modus.
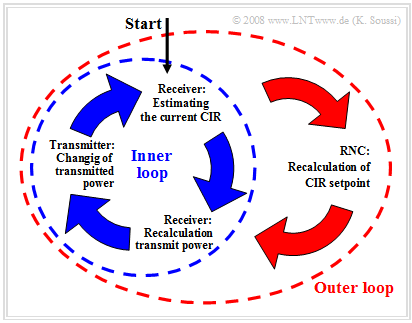
Wir betrachten die Leistungsregelung im FDD–Modus genauer. In der Grafik erkennt man zwei verschiedene Regelkreise:
- Der innere Regelkreis steuert die Sendeleistung auf der Basis von Zeitschlitzen, wobei in jedem Zeitschlitz ein Leistungskommando übertragen wird. Die Leistung des Senders wird mit Hilfe der CIR–Schätzungen im Empfänger und den Vorgaben des Radio Network Controllers (RNC) aus dem äußeren Regelkreis bestimmt und verändert.
- Der äußere Regelkreis regelt auf Basis von Rahmen mit $10$ Millisekunden Dauer. Er wird im RNC realisiert und ist dafür zuständig, den Soll–Wert für den inneren Regelkreis zu bestimmen.
Der Ablauf der FDD–Leistungsregelung sieht folgendermaßen aus:
- Der RNC gibt einen Sollwert für das Träger–zu–Interferenz–Verhältnis (CIR–Sollwert) vor.
- Der Empfänger schätzt den CIR–Istwert und generiert Steuerkommandos für den Sender.
- Der Sender ändert entsprechend dieser Steuerkommandos die Sendeleistung.
Das Prinzip der Leistungsregelung im TDD–Modus ähnelt der oben vorgestellten Regelung für den FDD–Modus, in der Abwärtsrichtung sind sie sogar praktisch identisch.
$\text{Fazit:}$ Die TDD–Leistungsregelung ist viel langsamer und dadurch auch unpräziser als bei FDD. Eine schnelle Leistungsregelung ist in diesem Fall aber auch gar nicht möglich, da jeder Teilnehmer jeweils nur einen Bruchteil des Zeitrahmens zur Verfügung hat.
Link–Budget
Bei der Planung von UMTS–Netzen ist die Berechnung des Link-Budgets ein wichtiger Schritt. Die Kenntnis des Link–Budgets ist sowohl bei der Dimensionierung der Versorgungsgebiete als auch für die Bestimmung der Kapazität und der Dienstgüte–Anforderungen erforderlich.
Ziel des Link–Budgets ist die Berechnung der maximalen Zellgröße unter Berücksichtigung folgender Kriterien:
- Art und Datenrate der Services,
- Topologie der Umgebung,
- Systemkonfiguration (Lage und Leistung der Basisstationen, Handover–Gewinn),
- Service–Anforderungen (Verfügbarkeit),
- Art der Mobilstation (Geschwindigkeit, Leistung),
- finanzielle und wirtschaftliche Aspekte.
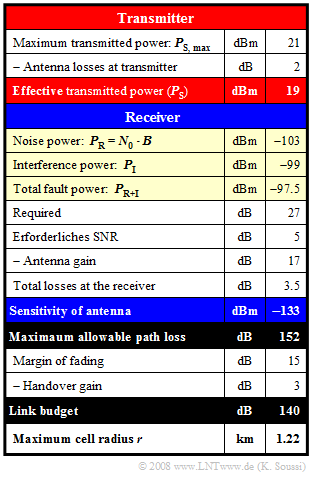
$\text{Beispiel 7:}$ Die Berechnung des Link–Budgets wird am Beispiel eines Sprachübertragungskanals im UMTS–Downlink dargestellt. Zu den beispielhaften Zahlenwerten ist zu bemerken:
- Die Sendeleistung betrage $P_{\rm S} =19 \ \rm dBm$, was ca. $79 \ \rm mW$ entspricht. Hierbei ist der Antennenverlust mit $2\ \rm dB$ berücksichtigt.
- Die Rauschleistung $P_{\rm R} = 5 · 10^{-11} \ \rm mW$ ist das Produkt aus UMTS–Bandbreite und Rauschleistungsdichte
⇒ $P_{\rm R} = -103 \ \rm dBm $. - Die Interferenzleistung ist $P_{\rm I} = –99\ \rm dBm$ entsprechend $1.25 · 10^{-10} \ \rm mW$.
- Damit ergibt sich die gesamte Störleistung zu $P_{\rm R+I} = P_{\rm R} + P_{\rm I} = 1.25 · 10^{-10} \ \rm mW$
⇒ $P_{\rm R+I} =- 97.5\ \rm dBm$. - Die Antennenempfindlichkeit ergibt sich zu $-97.5 - 27 + 5 - 17 + 3.5 = - 133 \ \rm dBm$. Ein großer negativer Wert ist hierbei „gut”.
- Der maximal zulässige Pfadverlust soll möglichst groß sein. Man erhält im Beispiel $19 - (-133) = 152 \ \rm dB$.
- Das Link–Budget beinhaltet den Margin für Fading und den Handover–Gewinn und beträgt im Beispiel $140 \ \rm dB$.
- Der maximale Zellradius lässt sich aus dem Link–Budget mit einer empirischen Formel von Okumura–Hata bestimmen. Es gilt:
- $$ {r}\ [{\rm km}] = 10^{({\rm LinkBudget}- 137)/35}= 10^{0.0857}\approx 1.22 . $$
Anmerkungen:
- Die Angabe $\rm dB$ kennzeichnet eine logarithmische Leistungsangabe, bezogen auf $1 \ \rm W$.
- Dagegen bezieht sich $\rm dBm$ auf die Leistung $1 \ \rm mW$.
UMTS–Funkressourcenverwaltung
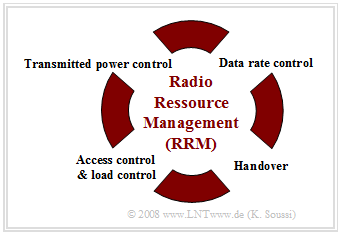
Zentrale Aufgabe der Funkressourcenverwaltung (englisch: Radio Resource Management, RRM) ist die dynamische Anpassung der Funkübertragungsparameter an die aktuelle Situation (Fading, Bewegung der Mobilstation, Auslastung, usw.) mit dem Ziel,
- die Übertragungs– und Teilnehmerkapazitäten zu steigern,
- die individuelle Übertragungsqualität zu verbessern und
- die vorhandenen Funkressourcen ökonomisch zu nutzen.
Nachfolgend werden die im Schaubild zusammengestellten wichtigsten RRM–Mechanismen erläutert.
Sendeleistungsregelung
Das Radio Resource Management versucht, die Empfangsleistung und damit das Träger–zu–Interferenz–Verhältnis (CIR) am Empfänger konstant zu halten oder zumindest zu vermeiden, dass ein vorgegebener Grenzwert unterschritten wird.
Ein Beispiel für die Notwendigkeit der Leistungsregelung ist der Near–Far–Effekt, der bekanntlich zu einem Verbindungsabbruch führen kann.
Die Schrittweite der Leistungsregelung beträgt $1 \ \rm dB$ oder $2 \ \rm dB$, die Frequenz der Regelungskommandos ist $1500$ Kommandos pro Sekunde.
Regelung der Datenrate
Bei UMTS ist ein Austausch zwischen Datenrate und Übertragungsqualität möglich, die sich über die Wahl des Spreizfaktors realisieren lässt. Eine Verdopplung des Spreizfaktors entspricht hierbei einer Halbierung der Datenrate und erhöht die Qualität um $3\ \rm dB$ (Spreizgewinn).
Zugangskontrolle
Um Überlastsituationen im Gesamtnetz zu vermeiden, wird vor dem Aufbau einer neuen Verbindung überprüft, ob die notwendigen Ressourcen vorhanden sind. Andernfalls wird die neue Verbindung abgewiesen. Diese Überprüfung wird durch Abschätzung der Sendeleistungsverteilung nach der Aufnahme der neuen Verbindung realisiert.
Lastregelung
Diese wird aktiv, wenn trotz Zugangskontrolle eine Überlast auftritt. In diesem Fall wird ein Handover zu einem anderen "Node B" initiiert und – falls dies nicht möglich ist – werden die Datenraten bestimmter Teilnehmer gesenkt.
Handover
Die Funkressourcenverwaltung ist schließlich auch für das Handover verantwortlich, um unterbrechungsfreie Verbindungen zu gewährleisten. Die Zuordnung der Mobilstationen zu den einzelnen Funkzellen erfolgt auf Grundlage von CIR–Messungen.
Aufgaben zum Kapitel
Aufgabe 4.5: Pseudo Noise-Modulation
Aufgabe 4.5Z: Zur Bandspreizung bei UMTS
Aufgabe 4.7: Zum Rake-Empfänger
Quellenverzeichnis
- ↑ 3gpp Group: UMTS Release 6 - Technical Specification 25.213 V6.4.0, Sept. 2005.