Approximation of the Error Probability

1 Optimal decision with binary transmission
2 The special case of equally probable binary symbols
3 Error probability for symbols with equal probability
4 Optimal threshold for non-equally probable symbols
5 Decision regions in the non-binary case
6 Error probability calculation in the non-binary case
7 Union Bound - Upper bound for the error probability
8 Weitere Aufwandsreduzierung bei der Union Bound
9 Aufgaben zum Kapitel

Optimal decision with binary transmission

We assume here a transmission system which can be characterized as follows: $\boldsymbol{r} = \boldsymbol{s} + \boldsymbol{n}$. This system has the following properties:

The vector space fully describing the transmission system is spanned by $N = 2$ mutually orthogonal basis functions $\varphi_1(t)$ and $\varphi_2(t)$.

Consequently, the probability density function of the additive and white Gaussian noise is also to be set two-dimensional, characterized by the vector $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$.

There are only two possible transmitted signals $(M = 2)$, described by the two vectors $\boldsymbol{ s_0} = (s_{01},\hspace{0.05cm}s_{02})$ and $\boldsymbol{ s_1} = (s_{11},\hspace{0.05cm}s_{12})$:

$$s_0(t)= s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm},\hspace{1cm}s_1(t) = s_{11} \cdot \varphi_1(t) + s_{12} \cdot \varphi_2(t) \hspace{0.05cm}.$$

The two messages $m_0 \ \Leftrightarrow \ \boldsymbol{ s_0}$ and $m_1 \ \Leftrightarrow \ \boldsymbol{ s_1}$ are not necessarily equally probable.

The task of the decision is to give an estimate for the current reception vector $\boldsymbol{r}$ according to the "MAP decision rule". In the present case, this rule is:

$$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm}|\hspace{0.05cm} m_i )\big ] \hspace{0.15cm} \in \hspace{0.15cm}\{ m_i\}\hspace{0.3cm}{\rm with}\hspace{0.3cm} \boldsymbol{ r } = \boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2) \hspace{0.05cm}.$$

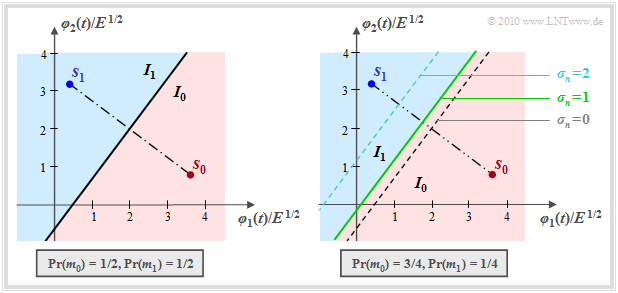
In the special case $N = 2$ and $M = 2$ considered here, the decision partitions the two-dimensional space into the two disjoint areas $I_0$ (highlighted in red) and $I_1$ (blue), as the following graphic illustrates. If the received value lies in $I_0$, $m_0$ is output as the estimated value, otherwise $m_1$.

Decision regions for equal (left) or unequal (right) occurrence probabilities

$\text{Derivation and picture description:}$ For the AWGN channel and $M = 2$, the decision rule is thus:

Always choose message $m_0$ if the following condition is satisfied:

$${\rm Pr}( m_0) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 \right ] > {\rm Pr}( m_1) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 \right ] \hspace{0.05cm}.$$

The boundary line between the two decision regions $I_0$ and $I_1$ is obtained by replacing the greater than sign with the equal sign in the above equation and transforming the equation slightly:

$$\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}\big [{\rm Pr}( m_0)\big ] = \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}\big [{\rm Pr}( m_1)\big ]$$

$$\Rightarrow \hspace{0.3cm} \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 + 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_0)}{ {\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$

From this plot one can see:

The boundary curve between regions $I_0$ and $I_1$ is a straight line, since the equation of determination is linear in the received vector $\boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2)$.

For equally probable symbols, the boundary is exactly halfway between $\boldsymbol{ s }_0$ and $\boldsymbol{ s }_1$ and rotated by $90^\circ$ with respect to the line connecting the transmitting points (left graph):

$$\vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert ^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert ^2 = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$

For ${\rm Pr}(m_0) > {\rm Pr}(m_1)$, the decision boundary is shifted toward the less likely symbol $\boldsymbol{ s }_1$, and the more so the larger the AWGN standard deviation $\sigma_n$.

The green-dashed decision boundary in the right figure as well as the decision regions $I_0$ (red) and $I_1$ (blue) are valid for the (normalized) standard deviation $\sigma_n = 1$ and the dashed boundary lines for $\sigma_n = 0$ and $\sigma_n = 2$, respectively.

The special case of equally probable binary symbols

We continue to assume a binary system $(M = 2)$, but now consider the simple case where this can be described by a single basis function $(N = 1)$. The error probability for this has already been calculated in the section "Definition of the Bit Error Probability".

With the nomenclature and representation form chosen for the fourth main chapter the following constellation results:

The received value $r = s + n$ is now a scalar and is composed of the transmitted signal $s \in \{s_0, \hspace{0.05cm}s_1\}$ and the noise term $n$ additively. The abscissa $\rho$ denotes a realization of $r$.

In addition, the abscissa is normalized to the reference quantity $\sqrt{E}$, whereas here the normalization energy $E$ has no prominent, physically interpretable meaning.

The noise term $n$ is Gaussian distributed with mean $m_n = 0$ and variance $\sigma_n^2$. The root of the variance $(\sigma_n)$ is called the rms value or the standard deviation.

The decision boundary $G$ divides the entire value range of $r$ into the two subranges $I_0$ $($in which, among other things, $s_0$ lies$)$ and $I_1$ $($with the signal value $s_1)$.

If $\rho > G$, the decision returns the estimated value $m_0$, otherwise $m_1$. Here it is assumed that the message $m_i$ is uniquely related to the transmitted signal $s_i$: $m_i \Leftrightarrow s_i$.

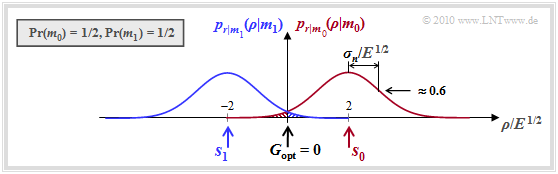
Conditional density functions for equal probability symbols

The graph shows the conditional (one-dimensional) probability density functions $p_{\hspace{0.02cm}r\hspace{0.05cm} \vert \hspace{0.05cm}m_0}$ and $p_{\hspace{0.02cm}r\hspace{0.05cm} \vert \hspace{0.05cm}m_1}$ for the AWGN channel, assuming equal symbol probabilities: ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. Thus, the (optimal) decision boundary is $G = 0$. One can see from this plot:

If $m = m_0$ and thus $s = s_0 = 2 \cdot E^{1/2}$, an erroneous decision occurs only if $\eta$, the realization of the noise quantity $n$, is smaller than $-2 \cdot E^{1/2}$. In this case, $\rho < 0$, where $\rho$ denotes a realization of the received value $r$.
In contrast, for $m = m_1$ ⇒ $s = s_1 = -2 \cdot E^{1/2}$, an erroneous decision occurs whenever $\eta$ is greater than $+2 \cdot E^{1/2}$. In this case, $\rho > 0$.

Error probability for symbols with equal probability

Let ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. For AWGN noise with rms (standard deviation) $\sigma_n$, as already calculated in the section "Definition of the bit error probability" with different nomenclature, we obtain for the probability of a wrong decision $(\cal E)$ under the condition that message $m_0$ was sent:

$${\rm Pr}({ \cal E}\hspace{0.05cm} \vert \hspace{0.05cm} m_0) = \int_{-\infty}^{G = 0} p_{r \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \rho } \hspace{0.05cm} \vert \hspace{0.05cm}m_0 ) \,{\rm d} \rho = \int_{-\infty}^{- s_0 } p_{{ n} \hspace{0.05cm}\vert\hspace{0.05cm}m_0 } ({ \eta } \hspace{0.05cm}|\hspace{0.05cm}m_0 ) \,{\rm d} \eta = \int_{-\infty}^{- s_0 } p_{{ n} } ({ \eta } ) \,{\rm d} \eta = \int_{ s_0 }^{\infty} p_{{ n} } ({ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {s_0 }/{\sigma_n} \right ) \hspace{0.05cm}.$$

In deriving the equation, it was considered that the AWGN noise $\eta$ is independent of the signal $(m_0$ or $m_1)$ and has a symmetric PDF. The complementary Gaussian error integral was also used

$${\rm Q}(x) = \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \hspace{0.05cm}.$$

Correspondingly, for $m = m_1$ ⇒ $s = s_1 = -2 \cdot E^{1/2}$:

$${\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1) = \int_{0}^{\infty} p_{{ r} \hspace{0.05cm}\vert\hspace{0.05cm}m_1 } ({ \rho } \hspace{0.05cm}\vert\hspace{0.05cm}m_1 ) \,{\rm d} \rho = \int_{- s_1 }^{\infty} p_{{ n} } (\boldsymbol{ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {- s_1 }/{\sigma_n} \right ) \hspace{0.05cm}.$$

$\text{Conclusion:}$ With the distance $d = s_1 - s_0$ of the signal space points, we can summarize the results, still considering ${\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$:

$${\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0) = {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1) = {\rm Q} \big ( {d}/(2{\sigma_n}) \big )$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_0) + {\rm Pr}(m_1) \cdot {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1)= \big [ {\rm Pr}(m_0) + {\rm Pr}(m_1) \big ] \cdot {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] \hspace{0.05cm}.$$

Notes:

This equation is valid under the condition $G = 0$ quite generally, thus also for ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$.
For "non-equally probable symbols", however, the error probability can be reduced by a different decision threshold.
The equation mentioned here is also valid if the signal space points are not scalars but are described by the vectors $\boldsymbol{ s}_0$ and $\boldsymbol{ s}_1$.
The distance $d$ results then as the norm of the difference vector: $d = \vert \hspace{-0.05cm} \vert \hspace{0.05cm} \boldsymbol{ s}_1 - \boldsymbol{ s}_0 \hspace{0.05cm} \vert \hspace{-0.05cm} \vert \hspace{0.05cm}.$

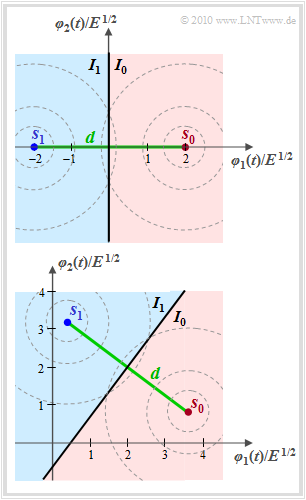
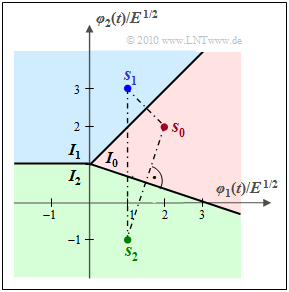
$\text{Example 1:}$ Let's look again at the signal space constellation from the "first chapter page" (lower graphic) with the values

Two signal space constellations

$\boldsymbol{ s}_0/E^{1/2} = (3.6, \hspace{0.05cm}0.8)$ and
$\boldsymbol{ s}_1/E^{1/2} = (0.4, \hspace{0.05cm}3.2)$.

Here the distance of the signal space points is

$$d = \vert \hspace{-0.05cm} \vert s_1 - s_0 \vert \hspace{-0.05cm} \vert = \sqrt{E \cdot (0.4 - 3.6)^2 + E \cdot (3.2 - 0.8)^2} = 4 \cdot \sqrt {E}\hspace{0.05cm}.$$

This results in exactly the same value as for the upper constellation with

$\boldsymbol{ s}_0/E^{1/2} = (2, \hspace{0.05cm}0)$ and
$\boldsymbol{ s}_1/E^{1/2} = (-2, \hspace{0.05cm}0)$.

The figures show these two constellations and reveal the following similarities and differences, respectively, assuming AWGN noise variance $\sigma_n^2 = N_0/2$ in each case. The circles in the graph illustrate the circular symmetry of 2D AWGN noise.

As said before, both the distance of the signal points from the decision line $(d/2 = 2 \cdot \sqrt {E})$ and the AWGN characteristic value $\sigma_n$ are the same in both cases.

It follows: The two arrangements lead to the same error probability if the parameter $E$ (a kind of normalization energy) is kept constant:

$${\rm Pr} ({\rm Symbolfehler}) = {\rm Pr}({ \cal E} ) = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ]\hspace{0.05cm}.$$

The mean energy per symbol $(E_{\rm S})$ for the upper constellation is given by

$$E_{\rm S} = 1/2 \cdot \vert \hspace{-0.05cm} \vert s_0 \vert \hspace{-0.05cm} \vert^2 + 1/2 \cdot \vert \hspace{-0.05cm} \vert s_1 \vert \hspace{-0.05cm} \vert^2 = E/2 \cdot \big[(+2)^2 + (-2)^2\big] = 4 \cdot {E}\hspace{0.05cm}.$$

With the lower constellation one receives in the same way:

$$E_{\rm S} = \ \text{...} \ = E/2 \cdot \big[(3.6)^2 + (0.8)^2\big] + E/2 \cdot \big[(0.4)^2 + (3.2)^2 \big] = 12 \cdot {E}\hspace{0.05cm}.$$

For a given mean energy per symbol $(E_{\rm S})$, the upper constellation is therefore clearly superior to the lower one: The same error probability results with one third of the energy per symbol. This issue will be discussed in detail in "Exercise 4.6Z".

Optimal threshold for non-equally probable symbols

If ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$ holds, a slightly smaller error probability can be obtained by shifting the decision boundary $G$. The following results are derived in detail in the sample solution to "Exercise 4.7":

For unequal symbol probabilities, the optimal decision boundary $G_{\rm opt}$ between regions $I_0$ and $I_1$ is closer to the less likely symbol.

The normalized optimal shift with respect to the limit $G = 0$ for equally probable symbols is

\[\gamma_{\rm opt} = \frac{G_{\rm opt}}{s_0 } = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm}.\]

The error probability is then equal to

$${\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Q} \big[ {d}/(2{\sigma_n}) \cdot (1 - \gamma_{\rm opt}) \big ] + {\rm Pr}(m_1) \cdot {\rm Q} \big [ {d}/(2{\sigma_n}) \cdot (1 + \gamma_{\rm opt}) \big ]\hspace{0.05cm}.$$

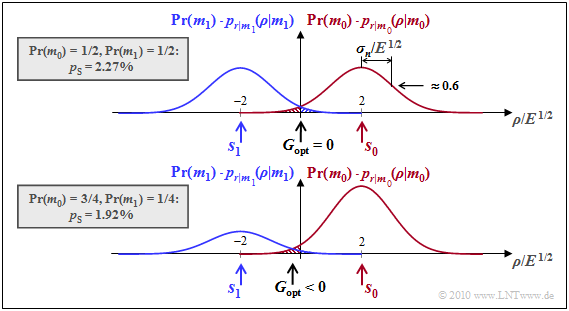
Density functions for equal/unequal symbol probabilities

$\text{Example 2:}$ The formal parameter $\rho$ (abscissa) again denotes a realization of the AWGN random variable $r = s + n$.

For the following is further valid:

$$\boldsymbol{ s }_0 = (2 \cdot \sqrt{E}, \hspace{0.1cm} 0), \hspace{0.2cm} \boldsymbol{ s }_1 = (- 2 \cdot \sqrt{E}, \hspace{0.1cm} 0)$$

$$ \Rightarrow \hspace{0.2cm} d = 2 \cdot \sqrt{E}, \hspace{0.2cm} \sigma_n = \sqrt{E} \hspace{0.05cm}.$$

For equally probable symbols ⇒ ${\rm Pr}( m_0) = {\rm Pr}( m_1) = 1/2$, the optimal decision boundary is $G_{\rm opt} = 0$ (see upper sketch). This gives us for the error probability:

$${\rm Pr}({ \cal E} ) = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] = {\rm Q} (2) \approx 2.26\% \hspace{0.05cm}.$$

Now we consider unequal symbol probabilities with ${\rm Pr}( m_0) = 3/4\hspace{0.05cm},\hspace{0.1cm}{\rm Pr}( m_1) = 1/4\hspace{0.05cm}$ (lower sketch). Let the other system variables be unchanged from the upper graph. In this case the optimal (normalized) shift factor is

\[\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_1)}{ {\rm Pr}( m_0)} = 2 \cdot \frac{ E}{16 \cdot E} \cdot {\rm ln} \hspace{0.15cm} \frac{1/4}{3/4 } \approx - 0.14 \hspace{0.05cm},\]

which is a $14\%$ shift toward the less likely symbol $\boldsymbol {s}_1$ (i.e., to the left). This makes the error probability slightly smaller than for equally likely symbols:

\[{\rm Pr}({ \cal E} )= 0.75 \cdot {\rm Q} \left ( 2 \cdot 1.14 \right ) + 0.25 \cdot {\rm Q} \left ( 2 \cdot 0.86 \right ) = 0.75 \cdot 0.0113 + 0.25 \cdot 0.0427 \approx 1.92\% \hspace{0.05cm}.\]

One recognizes from these numerical values:

Due to the threshold shift, the symbol $\boldsymbol {s}_1$ is now more distorted, but the more probable symbol $\boldsymbol {s}_0$ is distorted disproportionately less.

However, the result should not lead to misinterpretations. In the asymmetrical case ⇒ ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$ there is a smaller error probability than for ${\rm Pr}( m_0) ={\rm Pr}( m_1) = 0.5$, but then only less information can be transmitted with each symbol.
With the selected numerical values $0.81 \ \rm bit/symbol$ instead of $1\ \rm bit/symbol$. From an information theoretic point of view, ${\rm Pr}( m_0) ={\rm Pr}( m_1)$ would be optimal.

$\text{Conclusion:}$

In the symmetric case ⇒ ${\rm Pr}( m_0) ={\rm Pr}( m_1)$, the conventional conditional PDF values $p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$ can be used for decision.
In the asymmetric case ⇒ ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$, these functions must be weighted beforehand: ${\rm Pr}(m_i) \cdot p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m_i } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$.

In the following, we consider this issue.

Decision regions in the non-binary case

In general, the decision regions $I_i$ partition the $N$–dimensional real space into $M$ mutually disjoint regions. Here, $I_i$ is defined as the set of all points leading to the estimate $m_i$:

\[\boldsymbol{ \rho } \in I_i \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} \hat{m} = m_i, \hspace{0.3cm}{\rm where}\hspace{0.3cm}I_i = \left \{ \boldsymbol{ \rho } \in { \cal R}^N \hspace{0.05cm} | \hspace{0.05cm} {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm} | \hspace{0.05cm} m_i ) > {\rm Pr}( m_k) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm} | \hspace{0.05cm}m_k )\hspace{0.15cm} \forall k \ne i \right \} \hspace{0.05cm}.\]

The shape of the decision regions $I_i$ with $i = 0$, ... , $M-1$ in the $N$–dimensional space depend on the conditional probability density functions $p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m }$, i.e. on the considered channel.
In many cases – including the AWGN channel – the decision boundaries between every two signal points are even, which simplifies further considerations.

AWGN decision regions for
$N = 2$, $M = 3$

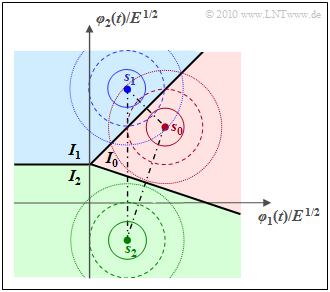
$\text{Example 3:}$ The graph shows the decision regions $I_0$, $I_1$ and $I_2$ for a transmission system with the parameters $N = 2$ and $M = 3$. The normalized transmission vectors here are

\[\boldsymbol{ s }_0 = (2,\hspace{0.05cm} 2), \hspace{0.2cm} \hspace{0.01cm} \boldsymbol{ s }_1 = (1,\hspace{0.05cm} 3), \hspace{0.01cm} \hspace{0.2cm} \boldsymbol{ s }_2 = (1,\hspace{0.05cm} -1) \hspace{0.05cm}.\]

Now two cases have to be distinguished:

For equally probable symbols ⇒ ${\rm Pr}( m_0) = {\rm Pr}( m_1) ={\rm Pr}( m_2) = 1/3 $, the boundaries between two regions are always straight, centered and perpendicular to the connecting lines.

In the case of unequal symbol probabilities, on the other hand, the decision boundaries are to be shifted in the direction of the more improbable symbol (parallel) in each case – the further the greater the AWGN standard deviation $\sigma_n$.

Error probability calculation in the non-binary case

After the decision regions $I_i$ are fixed, we can compute the symbol error probability of the overall system. We use the following names, although we sometimes have to use different names in continuous text than in equations because of the limitations imposed by our character set:

Symbol error probability: ${\rm Pr}({ \cal E} ) = {\rm Pr(symbol error)} \hspace{0.05cm},$

Probability of correct decision: ${\rm Pr}({ \cal C} ) = 1 - {\rm Pr}({ \cal E} ) = {\rm Pr(correct \hspace{0.15cm} decision)} \hspace{0.05cm},$

Conditional probability of a correct decision under the condition $m = m_i$: ${\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) \hspace{0.05cm}.$

With these definitions, the probability of a correct decision is:

\[{\rm Pr}({ \cal C} ) \hspace{-0.1cm} = \hspace{-0.1cm} \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } \hspace{0.05cm}.\]

For the AWGN channel, this is according to the section "$N$–dimensional Gaussian noise":

\[{\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) = \frac{1}{(\sqrt{2\pi} \cdot \sigma_n)^N} \cdot \int_{I_i} {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot || \boldsymbol{ \rho } - \boldsymbol{ s }_i ||^2 \right ] \,{\rm d} \boldsymbol {\rho }\hspace{0.05cm}.\]

This integral must be calculated numerically in the general case.
Only for a few, easily describable decision regions $\{I_i\}$ an analytical solution is possible.

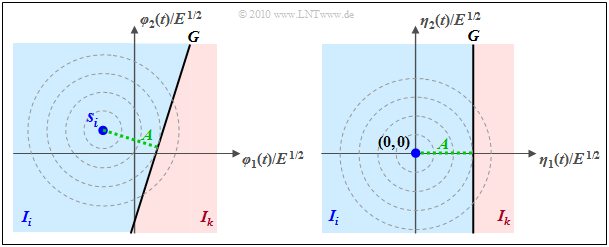
$\text{Example 4:}$ For the AWGN channel, there is a 2D Gaussian bell around the transmitting point $\boldsymbol{ s }_i$, recognizable in the left graphic by the concentric contour lines.

In addition, the decision line $G$ is drawn somewhat arbitrarily.
Shown on the right in a different coordinate system (shifted and rotated) is the PDF of the noise component alone.

To calculate the probability of error for AWGN

The graph can be interpreted as follows:

The probability that the received vector does not fall into the "target area" $I_i$, but into the red highlighted area $I_k$, is $ {\rm Q} (A/\sigma_n)$.
$A$ denotes the distance between $\boldsymbol{ s }_i$ and $G$.
$\sigma_n$ indicates the rms value (root of the variance) of the AWGN noise and ${\rm Q}(x)$ is the Gaussian error function.

Correspondingly, the probability for the event $r \in I_i$ is equal to the complementary value

\[{\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) = {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) = 1 - {\rm Q} (A/\sigma_n)\hspace{0.05cm}.\]

We now consider the equations given above

\[{\rm Pr}({ \cal C} ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.3cm}{\rm with} \hspace{0.3cm} {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } \hspace{0.05cm}\]

in a little more detail, where we again assume two basis functions $(N = 2)$ and three signal space points $\boldsymbol{ s }_0$, $\boldsymbol{ s }_1$ and $\boldsymbol{ s }_2$ $(M = 3)$.

Error probability calculation for AWGN channel and $M = 3$

The decision regions $I_0$, $I_1$ and $I_2$ are chosen best as possible.
The AWGN noise is indicated in the sketch by three circular contour lines each.

One can see from this plot:

Assuming that $m = m_i \ \Leftrightarrow \ \boldsymbol{ s } = \boldsymbol{ s }_i$ was sent, a correct decision is made only if the received value $\boldsymbol{ r }$ iis in region $I_i$.

The probability ${\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm}m_2)$ ist für $i = 2$ is (by far) largest for ⇒ correct decision. ${\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm}m_2)$ is much smaller. Almost negligible is ${\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm}m_2)$.

Thus, the falsification probabilities for $m = m_0$ and $m = m_1$ are:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 )={\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ),\]

\[ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) ={\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}.\]

The largest falsification probability is obtained for $m = m_0$. Because of

\[{\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \approx {\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}, \]

\[{\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \gg {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}\]

the following relations hold: ${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) > {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) >{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_2 )\hspace{0.05cm}. $

$\text{Conclusion:}$ These results can be summarized as follows:

To calculate the (average) error probability, it is necessary to average over all $M$ terms in general, even in the case of equally probable symbols.
In the case of equally probable symbols, ${\rm Pr}(m_i) = 1/M$ can be drawn in front of the summation, but this does not simplify the calculation procedure very much.
Only in the case of symmetrical arrangement the averaging can be omitted.

Union Bound - Upper bound for the error probability

For arbitrary values of $M$, the following applies to the falsification probability under the condition that the message $m_i$ $($or the signal $\boldsymbol{s}_i)$ has been sent:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.5cm}{ \cal E}_{ik}\hspace{-0.1cm}: \boldsymbol{ r }{\rm \hspace{0.15cm}is \hspace{0.15cm}closer \hspace{0.15cm}to \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}than \hspace{0.15cm}to \hspace{0.15cm}the \hspace{0.15cm}nominal \hspace{0.15cm}value \hspace{0.15cm}}\boldsymbol{ s }_i \hspace{0.05cm}. \]

$\text{Definition:}$ Für diesen Ausdruck lässt sich mit einer Booleschen Ungleichung – der so genannten Union Bound – eine obere Schranke angeben:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) \le \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1} {\rm Pr}({ \cal E}_{ik}) = \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1}{\rm Q} \big [ d_{ik}/(2{\sigma_n}) \big ]\hspace{0.05cm}. \]

Anmerkungen:

$d_{ik} = \vert \hspace{-0.05cm} \vert \boldsymbol{s}_i - \boldsymbol{s}_k \vert \hspace{-0.05cm} \vert$ ist der Abstand der Signalraumpunkte $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$.
$\sigma_n$ gibt den Effektivwert des AWGN–Rauschens an.
Die Union Bound ist nur bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}(m_i) = 1/M$ anwendbar.
Auch dann muss zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit über alle $m_i$ gemittelt werden.

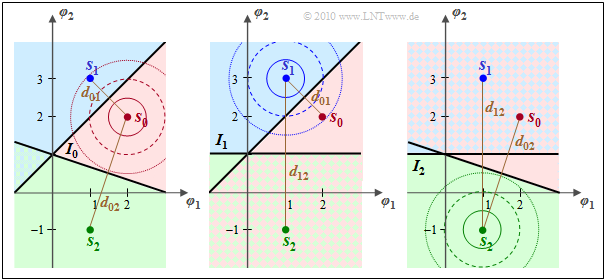
$\text{Beispiel 5:}$ Die Grafik verdeutlicht die Union Bound am Beispiel $M = 3$ mit gleichwahrscheinlichen Symbolen: ${\rm Pr}(m_0) = {\rm Pr}(m_1) = {\rm Pr}(m_2) =1/3$.

Zur Verdeutlichung der „Union Bound”

Zu diesen Darstellungen ist anzumerken:

Für die Symbolfehlerwahrscheinlichkeit gilt:

\[{\rm Pr}({ \cal E} ) = 1 - {\rm Pr}({ \cal C} ) \hspace{0.05cm},\hspace{0.2cm}{\rm Pr}({ \cal C} ) = {1}/{3} \cdot \big [ {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_1 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_2 ) \big ]\hspace{0.05cm}.\]

Der erste Term ${\rm Pr}(\boldsymbol{r} \in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ im Klammerausdruck unter der Voraussetzung $m = m_0 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_0$ ist in der linken Grafik durch die rote Region $I_0$ visualisiert.

Die Komplementärregion ${\rm Pr}(\boldsymbol{r} \not\in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ ist links entweder blau oder grün oder blau–grün schraffiert markiert. Es gilt ${\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = 1 - {\rm Pr}({ \cal E}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 )$ mit

$${\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\cup \hspace{0.05cm} \boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) \le {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) + {\rm Pr}(\boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) ={\rm Q} \big [ d_{01}/(2{\sigma_n}) \big ]+ {\rm Q} \big [ d_{02}/(2{\sigma_n}) \big ] \hspace{0.05cm}.$$

Das "$\le$"–Zeichen berücksichtigt hier, dass die blau–grün schraffierte Fläche sowohl zum Gebiet "$\boldsymbol{r} \in I_1$" als auch zum Gebiet "$\boldsymbol{r} \in I_2$" gehört, so dass die Summe einen zu großen Wert liefert. Das heißt: Die Union Bound liefert stets eine obere Schranke.

Die mittlere Grafik verdeutlicht die Berechnung der Union Bound unter der Voraussetzung, dass $m = m_1 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_1$ gesendet wurde.
Dem rechten Bild liegt $m = m_2 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_2$ zugrunde.

Weitere Aufwandsreduzierung bei der Union Bound

Zur Definition der Nachbarmengen $N(i)$

Die Abschätzung nach der "Union Bound" lässt sich weiter verbessern, indem man nur solche Signalraumpunkte berücksichtigt, die direkte Nachbarn des aktuellen Sendevektors $\boldsymbol{s}_i$ sind:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}{\rm Q}\big [ d_{ik}/(2{\sigma_n}) \big ] \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \hspace{0.05cm}\in \hspace{0.05cm}N(i)}^{M-1}\hspace{-0.4cm}{\rm Q} \big [ d_{ik}/(2{\sigma_n}) \big ] \hspace{0.05cm}. \]

Dazu definieren wir die Nachbarn von $\boldsymbol{s}_i$ als

\[N(i) = \left \{ k \in \left \{ i = 0, 1, 2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, M-1 \right \}\hspace{0.05cm}|\hspace{0.05cm} I_i {\rm \hspace{0.15cm}grenzt \hspace{0.15cm}direkt \hspace{0.15cm}an \hspace{0.15cm}}I_k \right \} \hspace{0.05cm}. \]

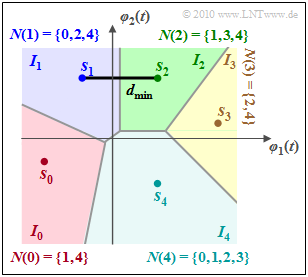
Die Grafik verdeutlicht diese Definiton am Beispiel $M = 5$. Die Regionen $I_0$ und $I_3$ haben jeweils nur zwei direkte Nachbarn, während $I_4$ an alle anderen Entscheidungsregionen angrenzt.

Durch die Einführung der Nachbarmengen $N(i)$ wird die Qualität der Union Bound–Approximation verbessert, das heißt, die Schranke liegt dann näher an der tatsächlichen Fehlerwahrscheinlichkeit, wird also nach unten verschoben.
Eine weitere und häufig verwendete Schranke benutzt nur den minimalen Abstand $d_{\rm min}$ zwischen zwei Signalraumpunkten. Im obigen Beispiel tritt dieser zwischen $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ auf. Für gleichwahrscheinliche Symbole ⇒ ${\rm Pr}(m_i) =1/M$ gilt dann die folgende Abschätzung:

\[{\rm Pr}({ \cal E} ) \le \sum\limits_{i = 0 }^{M-1} \left [ {\rm Pr}(m_i) \cdot \sum\limits_{k \ne i }{\rm Q} \big [d_{ik}/(2{\sigma_n})\big ] \right ] \le \frac{1}{M} \cdot \sum\limits_{i = 0 }^{M-1} \left [ \sum\limits_{k \ne i } {\rm Q} [d_{\rm min}/(2{\sigma_n})] \right ] = \sum\limits_{k \ne i }{\rm Q} \big [d_{\rm min}/(2{\sigma_n})\big ] = (M-1) \cdot {\rm Q} \big [d_{\rm min}/(2{\sigma_n})\big ] \hspace{0.05cm}. \]

Hierzu ist anzumerken:

Diese Schranke ist auch für große $M$–Werte sehr einfach zu berechnen. Bei vielen Anwendungen ergibt sich jedoch damit für die Fehlerwahrscheinlichkeit ein viel zu großer Wert.

Die Schranke ist nur dann gleich der tatsächlichen Fehlerwahrscheinlichkeit, wenn alle Regionen an alle anderen direkt angrenzen und die Distanzen aller $M$ Signalpunkte zueinander gleich $d_{\rm min}$ sind.

Im Sonderfall $M = 2$ sind diese beiden Voraussetzungen häufig erfüllt, so dass die Schranke exakt mit der tatsächlichen Fehlerwahrscheinlichkeit übereinstimmt.