Redundancy-Free Coding

Blockwise coding vs. symbolwise coding

In transmission coding, a distinction is made between two fundamentally different methods:

Symbolwise coding

Here, a code symbol $c_\nu$ is generated with each incoming source symbol $q_\nu$, which can depend not only on the current symbol but also on previous symbols $q_{\nu -1}$, $q_{\nu -2}$, ...
It is typical for all transmission codes for symbolwise coding that the symbol duration $T_c$ of the usually multilevel and redundant encoder signal $c(t)$ corresponds to the bit duration $T_q$ of the message source, which is assumed to be binary and redundancy-free.

Details can be found in the chapter Symbol-Wise Coding with Pseudo Ternary Codes.

Blockwise coding

Here, a block of $m_q$ binary source symbols $(M_q = 2)$ of bit duration $T_q$ is assigned a one–to–one sequence of $m_c$ code symbols from an alphabet with code symbol range $M_c \ge 2$.
For the symbol duration of a code symbol then holds:

$$T_c = \frac{m_q}{m_c} \cdot T_q \hspace{0.05cm},$$

The relative redundancy of a block code is in general

$$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.05cm}.$$

More detailed information on the block codes can be found in the chapter Block Coding with 4B3T Codes.

$\text{Example 1:}$ For the pseudoternary codes, increasing the number of stages from $M_q = 2$ to $M_c = 3$ for the same symbol duration $(T_c = T_q)$ adds a relative redundancy of $r_c = 1 - 1/\log_2 \hspace{0.05cm} (3) \approx 37\%$.

In contrast, the so-called 4B3T codes operate at block level with the code parameters $m_q = 4$, $M_q = 2$, $m_c = 3$ and $M_c = 3$ and have a relative redundancy of approx. $16\%$. Because of ${T_c}/{T_q} = 4/3$, the transmitted signal $s(t)$ is lower in frequency here than in uncoded transmission, which reduces the expensive bandwidth and is also advantageous for many message channels from a transmission point of view.

Quaternary signal with r_c = 0 and ternary signal with r_c ≈ 0

A special case of a block code is a redundancy-free multilevel code. Starting from the redundancy-free binary source signal $q(t)$ with bit duration $T_q$, a $M_c$–level code signal $c(t)$ with symbol duration $T_c = T_q \cdot \log_2 \hspace{0.05cm} (M_c)$ is generated. Thus, the relative redundancy is given by:

$$r_c = 1- \frac{T_c}{T_q \cdot {\rm log_2}\hspace{0.05cm} (M_c)} = 1- \frac{m_q}{m_c \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\to 0 \hspace{0.05cm}.$$

Thereby holds:

If $M_c$ is a power to the base $2$, then $m_q = \log_2 \hspace{0.05cm} (M_c)$ are combined into a single code symbol $(m_c = 1)$. In this case, the relative redundancy is actually $r_c = 0$.
If $M_c$ is not a power of two, a hundred percent redundancy-free block coding is not possible. For example, if $m_q = 3$ binary symbols are encoded by $m_c = 2$ ternary symbols and $T_c = 1.5 \cdot T_q$ is set, a relative redundancy of $r_c = 1-1.5/ \log_2 \hspace{0.05cm} (3) \approx 5\%$ remains.
Encoding a block of $128$ binary symbols with $81$ ternary symbols results in a relative code redundancy of less than $r_c = 0.3\%$.

To simplify the notation and to align the nomenclature with the first main chapter, we use in the following

the bit duration $T_{\rm B} = T_q$ of the redundancy-free binary source signal,
the symbol duration $T = T_c$ of the encoder signal and the transmitted signal, and
the number of steps $M = M_c$.

This results in the identical form for the transmitted signal as for the binary transmission, but with different amplitude coefficients:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm with}\hspace{0.3cm} a_\nu \in \{ a_1, \text{...} , a_\mu , \text{...} , a_{ M}\}\hspace{0.05cm}.$$

In principle, the amplitude coefficients $a_\nu$ can be assigned arbitrarily – but uniquely – to the encoder symbols $c_\nu$. It is convenient to choose equal distances between adjacent amplitude coefficients.
Thus, for bipolar signaling $(-1 \le a_\nu \le +1)$, the following applies to the possible amplitude coefficients with index $\mu = 1$, ... , $M$:

$$a_\mu = \frac{2\mu - M - 1}{M-1} \hspace{0.05cm}.$$

Independently of the number of steps $M$ one obtains from this for the outer amplitude coefficients $a_1 = -1$ and $a_M = +1$.
For a ternary signal $(M = 3)$, the possible amplitude coefficients are $-1$, $0$ and $+1$.
For a quaternary signal $(M = 4)$, the coefficients are $-1$, $-1/3$, $+1/3$ and $+1$.

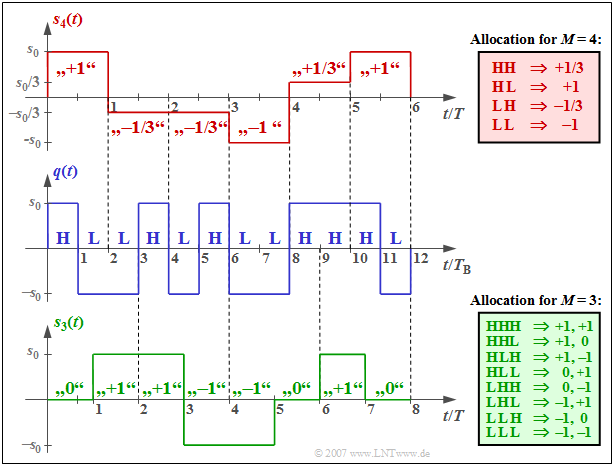
$\text{Example 2:}$ The graphic above shows the quaternary redundancy-free transmitted signal $s_4(t)$ with the possible amplitude coefficients $\pm 1$ and $\pm 1/3$, which results from the binary source signal $q(t)$ shown in the center.

Two binary symbols each are combined to a quaternary amplitude coefficient according to the table with red background. The symbol duration $T$ of the signal $s_4(t)$ is twice the bit duration $T_{\rm B}$ (previously: $T_q$) of the source signal.

If $q(t)$ is redundancy-free, it also results in a redundancy-free quaternary signal, i.e., the possible amplitude coefficients $\pm 1$ and $\pm 1/3$ are equally probable and there are no statistical ties within the sequence $⟨a_ν⟩$.

Redundancy-free ternary and quaternary signal

The lower plot shows the (almost) redundancy-free ternary signal $s_3(t)$ and the mapping of three binary symbols each to two ternary symbols.

The possible amplitude coefficients are $-1$, $0$ and $+1$ and $T/T_{\rm B} = 3/2$.
It can be seen from the green mapping table that the amplitude coefficients $+1$ and $-1$ occur somewhat more frequently than the amplitude coefficient $a_\nu = 0$.
This results in the above mentioned relative redundancy of $5\%$.
However, from the very short signal section – only eight ternary symbols corresponding to twelve binary symbols – this property is not apparent.

ACF and PSD of a multilevel signal

For a redundancy-free coded $M$–level bipolar digital signal $s(t)$, the following holds for the discrete auto-correlation function (ACF) of the amplitude coefficients and for the corresponding power-spectral density (PSD):

$$\varphi_a(\lambda) = \left\{ \begin{array}{c} \frac{M+ 1}{3 \cdot (M-1)} \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\\ \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \\ \end{array} \hspace{0.9cm}\Rightarrow \hspace{0.9cm}{\it \Phi_a(f)} = \frac{M+ 1}{3 \cdot (M-1)}= {\rm const.}$$

Considering the spectral shaping by the basic transmission pulse $g_s(t)$ with spectrum $G_s(f)$, we obtain:

$$\varphi_{s}(\tau) = \frac{M+ 1}{3 \cdot (M-1)} \cdot \varphi^{^{\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_{s}(f) = \frac{M+ 1}{3 \cdot (M-1)}\cdot |G_s(f)|^2 \hspace{0.05cm}.$$

One can see from these equations:

In the case of redundancy-free multilevel coding, the shape of ACF and PSD is determined solely by the basic transmission pulse $g_s(t)$.
The magnitude of the ACF is lower than the redundancy-free binary signal by a factor $\varphi_a(\lambda = 0) = {\rm E}\big[a_\nu^2\big] = (M + 1)/(3M-3)$ for the same shape.
This factor describes the lower signal power of the multilevel signal due to the $M-2$ inner amplitude coefficients.
For $M = 3$ this factor is equal to $2/3$, for $M = 4$ it is equal to $5/9$.
However, a fair comparison between binary signal and multilevel signal with the same information flow (same equivalent bit rate) should also take into account the different symbol durations.
This shows that a multilevel signal requires less bandwidth than the binary signal due to the narrower PSD when the same information is transmitted.

$\text{Example 3:}$ We assume a binary source with bit rate $R_{\rm B} = 1 \ \rm Mbit/s$, so that the bit duration $T_{\rm B} = 1 \ \rm µ s$.

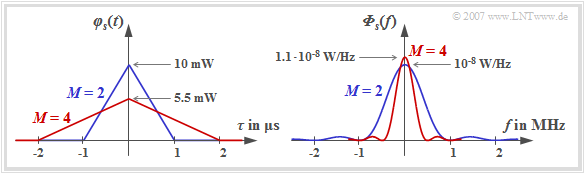
For binary transmission $(M = 2)$, the symbol duration $T$ of the transmitted signal is equal to $T_{\rm B}$ and the auto-correlation function shown in blue in the left graph results for NRZ rectangular pulses (assuming $s_0^2 = 10 \ \rm mW$).
For the quaternary system $(M = 4)$, the ACF is also triangular, but lower by a factor of $5/9$ and twice as wide because of $T = 2 \cdot T_{\rm B}$.

ACF and PSD of binary and quaternary signal

The $\rm sinc^2$–shaped power-spectral density in the binary case (blue curve) has the maximum value ${\it \Phi}_{s}(f = 0) = 10^{-8} \ \rm W/Hz$ (area of the blue triangle) for the signal parameters selected here and the first zero point is at $f = 1 \ \rm MHz$.

The power-spectral density of the quaternary signal (red curve) is only half as wide and slightly higher. Here ${\it \Phi}_{s}(f = 0) \approx 1.1 \cdot 10^{-8} \ \rm W/Hz$ is valid.
The value results from the area of the red triangle. This is lower $($factor $0.55)$ and wider (factor $2$).

Error probability of a multilevel system

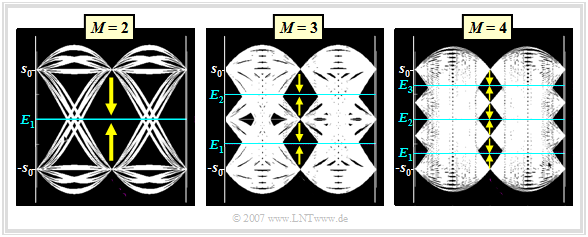
Eye diagrams for redundancy–free binary, ternary and quaternary signals

The diagram shows the eye diagrams

of a binary transmission system $(M = 2)$,
a ternary transmission system $(M = 3)$ and
a quaternary transmission system $(M = 4)$.

Here, a cosine rolloff characteristic is assumed for the overall system $H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f)$ of transmitter, channel and receiver, so that intersymbol interference does not play a role. The rolloff factor is $r= 0.5$. The noise is assumed to be negligible.

The eye diagram is used to estimate intersymbol interference. A detailed description follows in the section Definition and statements of the eye diagram. However, the following text should be understandable even without detailed knowledge.

It can be seen from the above diagrams:

In the binary system $(M = 2)$, there is only one decision threshold: $E_1 = 0$. A transmission error occurs if the noise component $d_{\rm N}(T_{\rm D})$ at the time of detection is greater than $+s_0$ $\big ($if $d_{\rm S}(T_{\rm D}) = -s_0$ $\big )$ or if $d_{\rm N}(T_{\rm D})$ is less than $-s_0$ $\big ($if $d_{\rm S}(T_{\rm D}) = +s_0$ $\big )$.

In the case of the ternary system $(M = 3)$, two eye openings and two decision thresholds $E_1 = -s_0/2$ and $E_2 = +s_0/2$ can be recognized. The distance of the possible detection useful signal values $d_{\rm S}(T_{\rm D})$ to the nearest threshold is $-s_0/2$ in each case. The outer amplitude values $(d_{\rm S}(T_{\rm D}) = \pm s_0)$ can only be falsified in one direction in each case, while $d_{\rm S}(T_{\rm D}) = 0$ is limited by two thresholds.

Accordingly, an amplitude coefficient $a_\nu = 0$ is falsified twice as often compared to $a_\nu = +1$ or $a_\nu = -1$. For AWGN noise with rms value $\sigma_d$ as well as equal probability amplitude coefficients, according to the section Definition of the bit error probability for the symbol error probability:

$$p_{\rm S} = { 1}/{3} \cdot \left[{\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)+ 2 \cdot {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)+ {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)\right]= \frac{ 4}{3} \cdot {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)\hspace{0.05cm}.$$

Please note that this equation no longer specifies the bit error probability $p_{\rm B}$, but the symbol error probability $p_{\rm S}$. The corresponding a posteriori parameters are Bit Error Rate (BER) and Symbol Error Rate (SER). More details are given in the last section of this chapter.

Beim Quaternärsystem $(M = 4)$ mit den möglichen Amplitudenwerten $\pm s_0$ und $\pm s_0/3$ gibt es drei Augenöffnungen und somit auch drei Entscheiderschwellen bei $E_1 = -2s_0/3$, $E_2 = 0$ und $E_3 = +2s_0/3$. Unter Berücksichtigung der Auftrittswahrscheinlichkeiten $($bei gleichwahrscheinlichen Symbolen jeweils $1/4)$ und der sechs Verfälschungsmöglichkeiten (siehe Pfeile in der Grafik) erhält man nun:

$$p_{\rm S} = { 6}/{4} \cdot {\rm Q} \left( \frac{s_0/3}{\sigma_d}\right)\hspace{0.05cm}.$$

$\text{Fazit:}$ Allgemein gilt für die Symbolfehlerwahrscheinlichkeit bei $M$–stufiger Digitalsignalübertragung:

$$p_{\rm S} = \frac{ 2 + 2 \cdot (M-2)}{M} \cdot {\rm Q} \left( \frac{s_0/(M-1)}{\sigma_d(M)}\right) = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \frac{s_0}{\sigma_d (M)\cdot (M-1)}\right)\hspace{0.05cm}.$$

Die Schreibweise $\sigma_d(M)$ soll deutlich machen, dass der Effektivwert des Rauschanteils $d_{\rm N}(t)$ signifikant von der Stufenzahl $M$ abhängt.

Vergleich zwischen Binärsystem und Mehrstufensystem

Für diesen Systemvergleich unter fairen Bedingungen werden vorausgesetzt:

Die äquivalente Bitrate $R_{\rm B} = 1/T_{\rm B}$ sei konstant. Abhängig von der Stufenzahl $M$ beträgt somit die Symboldauer von Codersignal und Sendesignal:

$$T = T_{\rm B} \cdot {\rm log_2} (M) \hspace{0.05cm}.$$

Die Nyquistbedingung wird durch eine Wurzel–Wurzel–Charakteristik mit Rolloff–Faktor $r$ erfüllt. Es treten weiterhin keine Impulsinterferenzen auf. Für die Detektionsrauschleistung gilt:

$$\sigma_d^2 = \frac{N_0}{2T} \hspace{0.05cm}.$$

Der Vergleich der Symbolfehlerwahrscheinlichkeiten $p_{\rm S}$ erfolgt für Leistungsbegrenzung. Die Energie pro Bit beträgt bei $M$–stufiger Übertragung:

$$E_{\rm B} = \frac{M+ 1}{3 \cdot (M-1)} \cdot s_0^2 \cdot T_{\rm B} \hspace{0.05cm}.$$

Setzt man diese Gleichungen in das allgemeine Ergebnis der letzten Seite ein, so erhält man:

$$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \sqrt{\frac{s_0^2 /(M-1)^2}{\sigma_d^2}}\right) = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \sqrt{\frac{3 \cdot {\rm log_2}\hspace{0.05cm} (M)}{M^2 -1}\cdot \frac{2 \cdot E_{\rm B}}{N_0}}\right)= K_1 \cdot {\rm Q} \left( \sqrt{K_2\cdot \frac{2 \cdot E_{\rm B}}{N_0}}\right)\hspace{0.05cm}.$$

Für $M = 2$ ist $K_1 = K_2 = 1$ zu setzen. Für größere Stufenzahlen erhält man für die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$, die sich mit $M$–stufiger redundanzfreier Codierung erreichen lässt:

Symbolfehlerwahrscheinlichkeitskurven für verschiedene Stufenzahlen $M$

$$M = 3\text{:} \ \ K_1 = 1.333, \ K_2 = 0.594;\hspace{0.5cm}M = 4\text{:} \ \ K_1 = 1.500, \ K_2 = 0.400;$$

$$M = 5\text{:} \ \ K_1 = 1.600, \ K_2 = 0.290;\hspace{0.5cm}M = 6\text{:} \ \ K_1 = 1.666, \ K_2 = 0.221;$$

$$M = 7\text{:} \ \ K_1 = 1.714, \ K_2 = 0.175;\hspace{0.5cm}M = 8\text{:} \ \ K_1 = 1.750, \ K_2 = 0.143.$$

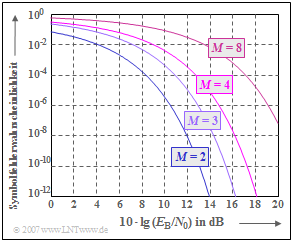
Die Grafik fasst die Ergebnisse für $M$–stufige redundanzfreie Codierung zusammen.

Aufgetragen sind die Symbolfehlerwahrscheinlichkeiten $p_{\rm S}$ über der Abszisse $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0)$.
Alle Systeme sind für das jeweilige $M$ optimal, wenn man vom AWGN–Kanal und Leistungsbegrenzung ausgeht.
Aufgrund der hier gewählten doppelt–logarithmischen Darstellung führt ein $K_2$–Wert kleiner als $1$ zu einer Parallelverschiebung der Fehlerwahrscheinlichkeitskurve nach rechts.
Gilt $K_1 > 1$, so verschiebt sich die Kurve gegenüber dem Binärsystem $(K_1= 1)$ nach oben.

$\text{Systemvergleich unter der Nebenbedingung Leistungsbegrenzung:}$
Die obigen Kurvenverläufe kann man wie folgt interpretieren:

Hinsichtlich Symbolfehlerwahrscheinlichkeit ist das Binärsystem $(M = 2)$ den Mehrstufensystemen überlegen. Bereits mit $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) = 12 \ \rm dB$ erreicht man $p_{\rm S} <10^{-8}$. Beim Quaternärsystem $(M = 4)$ muss $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) > 16 \ \rm dB$ aufgewendet werden, um die gleiche Symbolfehlerwahrscheinlichkeit $p_{\rm S} =10^{-8}$ zu erreichen.
Diese Aussage gilt jedoch nur bei verzerrungsfreiem Kanal, das heißt für $H_{\rm K}(f)= 1$. Bei verzerrenden Übertragungskanälen kann dagegen ein höherstufiges System wegen der signifikant kleineren Detektionsstörleistung (nach dem Entzerrer) eine deutliche Verbesserung bringen.
Beim AWGN–Kanal ist der einzige Vorteil einer höherstufigen Übertragung der niedrigere Bandbreitenbedarf aufgrund der kleineren äquivalenten Bitrate, der bei Basisbandübertragung nur eine untergeordnete Rolle spielt im Gegensatz zu digitalen Trägerfrequenzsystemen, z. B. Quadratur–Amplitudenmodulation (QAM).

$\text{Systemvergleich unter der Nebenbedingung Spitzenwertbegrenzung:}$

Mit der Nebenbedingung "Spitzenwertbegrenzung" führt die Kombination aus rechteckförmigem $g_s(t)$ und rechteckförmigem $h_{\rm E}(t)$ unabhängig von der Stufenzahl $M$ zum Optimum.
Der Verlust der Mehrstufensystemen gegenüber dem Binärsystem ist hier noch größer als bei Leistungsbegrenzung. Dies erkennt man an dem mit $M$ abnehmenden Faktor $K_2$, für den dann gilt:

$$p_{\rm S} = K_1 \cdot {\rm Q} \left( \sqrt{K_2\cdot \frac{2 \cdot s_{\rm 0}^2 \cdot T}{N_0} }\right)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} K_2 = \frac{ {\rm log_2}\,(M)}{(M-1)^2} \hspace{0.05cm}.$$

Die Konstante $K_1$ ist gegenüber der obigen Angabe für Leistungsbegrenzung unverändert, während $K_2$ um den Faktor $3$ kleiner ist:

$$M = 3\text{:} \ \ K_1 = 1.333, \ K_2 = 0.198;\hspace{1cm}M = 4\text{:} \ \ K_1 = 1.500, \ K_2 = 0.133;$$

$$M = 5\text{:} \ \ K_1 = 1.600, \ K_2 = 0.097;\hspace{1cm}M = 6\text{:} \ \ K_1 = 1.666, \ K_2 = 0.074;$$

$$M = 7\text{:} \ \ K_1 = 1.714, \ K_2 = 0.058;\hspace{1cm}M = 8\text{:} \ \ K_1 = 1.750, \ K_2 = 0.048.$$

Symbol and bit error probability

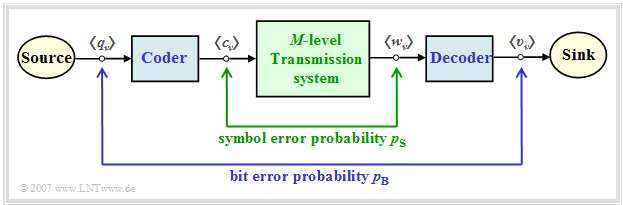
Bei einem mehrstufigen Übertragungssystem muss man zwischen der Symbolfehlerwahrscheinlichkeit und der Bitfehlerwahrscheinlichkeit unterscheiden, die hier sowohl als Scharmittelwerte als auch als Zeitmittelwerte angegeben werden:

Die Symbolfehlerwahrscheinlichkeit bezieht sich auf die $M$–stufigen und eventuell redundanten Folgen $\langle c_\nu \rangle$ und $\langle w_\nu \rangle$:

$$p_{\rm S} = \overline{{\rm Pr} (w_\nu \ne c_\nu)} = \lim_{N \to \infty} \frac{1}{N} \cdot \sum \limits^{N} _{\nu = 1} {\rm Pr} (w_\nu \ne c_\nu) \hspace{0.05cm}.$$

Die Bitfehlerwahrscheinlichkeit beschreibt die Verfälschungen bezüglich der Binärfolgen $\langle q_\nu \rangle$ und $\langle v_\nu \rangle$ von Quelle und Sinke:

$$p_{\rm B} = \overline{{\rm Pr} (v_\nu \ne q_\nu)} = \lim_{N \to \infty} \frac{1}{N} \cdot \sum \limits^{N} _{\nu = 1} {\rm Pr} (v_\nu \ne q_\nu) \hspace{0.05cm}.$$

Die Grafik veranschaulicht diese beiden Definitionen und ist auch für die nächsten Kapitel gültig. Der Block "Coder" bewirkt

im vorliegenden Kapitel eine redundanzfreie Codierung,
im anschließendem Kapitel eine blockweise Übertragungscodierung, und schließlich
im letzten Kapitel die symbolweise Codierung mit Pseudoternärcodes.

Symbolfehlerwahrscheinlichkeit und Bitfehlerwahrscheinlichkeit

$\text{Fazit:}$

Bei mehrstufiger und(oder codierter Übertragung muss zwischen der Bitfehlerwahrscheinlichkeit $p_{\rm B}$ und der Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ unterschieden werden. Nur beim redundanzfreien Binärsystem gilt $p_{\rm B} = p_{\rm S}$.
Im allgemeinen kann bei redundanzbehafteten Mehrstufensystem die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ etwas einfacher berechnet werden als die Bitfehlerwahrscheinlichkeit $p_{\rm B}$.
Ein Vergleich von Systemen mit unterschiedlicher Stufenzahl oder verschiedenartiger Codierung sollte aber aus Fairnisgründen stets auf der Bitfehlerwahrscheinlichkeit $p_{\rm B}$ basieren.
Dabei muss auch die Zuordnung zwischen den Quellen– und Codesymbolen berücksichtigt werden, wie im folgenden Beispiel gezeigt wird.

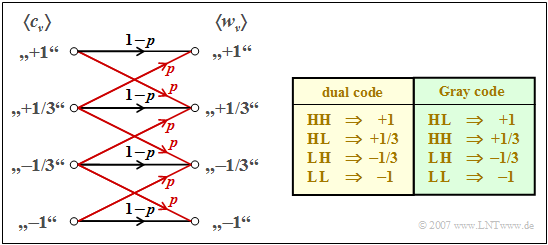
$\text{Beispiel 4:}$ Wir betrachten ein quaternäres Übertragungssystem, dessen Übertragungsverhalten wie folgt charakterisiert werden kann (siehe linke Grafik):

Die Verfälschungswahrscheinlichkeit zu einem benachbarten Symbol ist $p={\rm Q}\big [s_0/(3\sigma_d)\big ]$.
Eine Verfälschung zu einem nicht benachbarten Symbol wird ausgeschlossen.
Das Modell berücksichtigt die doppelten Verfälschungsmöglichkeiten der inneren Symbole.

Gegenüberstellung von Graycode und Dualcode

Bei gleichwahrscheinlichen binären Quellensymbolen $q_\nu$ treten auch die quaternären Codesymbole $c_\nu$ mit gleicher Wahrscheinlichkeit auf. Damit erhält man für die Symbolfehlerwahrscheinlichkeit:

$$p_{\rm S} ={1}/{4}\cdot (2 \cdot p + 2 \cdot 2 \cdot p) = {3}/{2} \cdot p\hspace{0.05cm}.$$

Zur Berechnung der Bitfehlerwahrscheinlichkeit muss man auch die Zuordnung zwischen den Binär– und den Quaternärsymbolen berücksichtigen:

Bei der Dualcodierung gemäß der gelb hinterlegten Tabelle kann ein Symbolfehler $(w_\nu \ne c_\nu)$ ein oder zwei Bitfehler $(v_\nu \ne q_\nu)$ zur Folge haben. Von den sechs Verfälschungsmöglichkeiten auf Quaternärsymbolebene führen vier zu jeweils einem und nur die beiden inneren zu zwei Bitfehlern. Daraus folgt:

$$p_{\rm B} = {1}/{4}\cdot (4 \cdot 1 \cdot p + 2 \cdot 2 \cdot p ) \cdot {1}/{2} = p\hspace{0.05cm}.$$

Der Faktor $1/2$ berücksichtigt, dass ein Quaternärsymbol zwei Binärsymbole beinhaltet.

Dagegen ist bei der so genannten Graycodierung gemäß der grün hinterlegten Tabelle die Zuordnung zwischen den Binärsymbolen und den Quaternärsymbolen so gewählt, dass jeder Symbolfehler genau einen Bitfehler zur Folge hat. Daraus folgt:

$$p_{\rm B} = {1}/{4}\cdot (4 \cdot 1 \cdot p + 2 \cdot 1 \cdot p ) \cdot {1}/{2} = {3}/{4} \cdot p\hspace{0.05cm}.$$