Difference between revisions of "Linear and Time Invariant Systems/System Description in Frequency Domain"
| (236 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
{{FirstPage}} | {{FirstPage}} | ||
{{Header| | {{Header| | ||
| − | Untermenü= | + | Untermenü=Basics of System Theory |
| − | |Nächste Seite= | + | |Nächste Seite=System Description in Time Domain |
}} | }} | ||
| − | == | + | == # OVERVIEW OF THE FIRST MAIN CHAPTER # == |
| + | <br> | ||
| + | *In the book »Signal Representation« you were familiarized with the mathematical description of deterministic signals in the time and frequency domain. | ||
| − | + | *The second book »Linear Time-Invariant Systems« now describes what changes a signal or its spectrum undergoes through a transmission system and how these changes can be captured mathematically. | |
| − | + | *In the first chapter, the basics of the so-called »Systems Theory« are mentioned, which allows a uniform and simple description of such systems. We start with the system description in the frequency domain with the partial aspects listed above. | |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Please note:}$ | ||
| + | *The »'''system'''« can be a simple circuit as well as a complete, highly complicated transmission system with a multitude of components. | ||
| − | * | + | *Here it is only assumed that the system has the two properties »'''linear'''« and »'''time-invariant'''«.}} |
| − | |||
| − | |||
| − | + | ==The cause-and-effect principle== | |
| + | <br> | ||
| + | [[File:P_ID775__LZI_T_1_1_S1_neu.png|right|frame|Simplest system model|class=fit]] | ||
| + | We always consider here the simple model outlined on the right. This arrangement is to be interpreted as follows: | ||
| − | == | + | *The focus is on the so-called »system«, which is largely abstracted in its function ⇒ »black box«. Nothing is known in detail about the realization of the system. |
| − | + | ||
| + | *The time-dependent input $x(t)$ acting on this system is also referred to as the »'''cause function'''« in the following. | ||
| + | |||
| + | *At the system output, the »'''effect function'''« $y(t)$ appears as the system response to the input function $x(t)$. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Please note:}$ | ||
| + | |||
| + | #The »system« can generally be of any kind and is not limited to communications technology alone. In fact, attempts are also made in other fields of science, such as the natural sciences, economics and business administration, sociology and political science, to capture and describe causal relationships between different variables by means of the cause-and-effect principle. | ||
| + | #However, the methods used for these phenomenological systems theories differ significantly from the approach in Communications Engineering, which is outlined in this first main chapter of the present book »Linear Time-Invariant Systems«.}} | ||
| + | |||
| + | ==Application in Communications Engineering== | ||
| + | <br> | ||
| + | The cause-and-effect principle can be applied in Communications Engineering, for example to describe one-port circuits which are also reffered to as one-ports. Here, one can consider the current curve $i(t)$ as a cause function and the voltage $u(t)$ as an effect function. By observing the I/U relationships, conclusions can be drawn about the properties of the actually unknown one-port. | ||
| + | |||
| + | [[File:EN_LZI_T_1_1_S2.png|right|frame|General model of signal transmission|class=fit]] | ||
| + | In Germany, [https://en.wikipedia.org/wiki/Karl_K%C3%BCpfm%C3%BCller $\text{Karl Küpfmüller}$] introduced the term »Systems Theory« for the first time in 1949. | ||
| + | He considers it as a method for describing complex causal relationships in natural sciences and technology, based on a spectral transformation, e.g. the | ||
| + | [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»Fourier transform«]]. | ||
| − | + | A transmission system can entirely be described in terms of systems theory . Here | |
| + | *the »cause function« is the input signal $x(t)$ or its spectrum $X(f)$, | ||
| + | |||
| + | *the »effect function« is the output signal $y(t)$ or its spectrum $Y(f)$. | ||
| − | |||
| − | + | Also in the following graphs, input variables are mostly drawn in blue, output variables in red and system variables in green. | |
| + | <br clear=all> | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 1:}$ | ||
| − | + | (1) For example, if the »system« describes a given linear electric circuit, then given a known input signal $x(t)$ the output signal $y(t)$ can be predicted with the help of "Systems Theory". | |
| − | + | (2) A second task of "Systems Theory" is to classify the transmission system by measuring $y(t)$ knowing $x(t)$ but without knowing the system in detail. | |
| − | |||
| − | + | (3) If $x(t)$ describes, for instance, the voice of a caller in Hamburg and $y(t)$ the recording of an answering machine in Munich, then the »transmission system« consists of the following components: | |
| − | + | :Microphone – telephone – electrical line – signal converter $($electrical-optical$)$ – fiber optic cable – optical amplifier – signal converter $($optical-electrical$)$ – receiver filter $($for equalization and noise limitation$)$ – . . . . . . – electromagnetic transducer. }} | |
| − | |||
| − | == | + | ==Prerequisites for the application of Systems Theory== |
| − | + | <br> | |
| − | + | The model of a transmission system given above holds generally and independently of the boundary conditions. However, the application of systems theory requires some additional limiting preconditions. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Unless explicitly stated otherwise, the following shall always apply: | |
| + | *Both $x(t)$ and $y(t)$ are »'''deterministic'''« signals. Otherwise, one must proceed according to the chapter [[Theory_of_Stochastic_Signals/Stochastische_Systemtheorie|»Stochastic System Theory«]]. | ||
| − | + | *The system is »'''linear'''«. This can be seen, for example, from the fact that a harmonic oscillation $x(t)$ at the input also results in a harmonic oscillation $y(t)$ of the same frequency at the output: | |
| − | + | :$$x(t) = A_x \cdot \cos(\omega_0 \hspace{0.05cm}t - \varphi_x)\hspace{0.2cm}\Rightarrow \hspace{0.2cm} y(t) = A_y \cdot\cos(\omega_0 \hspace{0.05cm}t - \varphi_y).$$ | |
| + | *New frequencies do not arise. Only amplitude and phase of the harmonic oscillation can be changed. Nonlinear systems are treated in the chapter [[Linear_and_Time_Invariant_Systems/Nonlinear_Distortions|»Nonlinear Distortions«]]. | ||
| − | + | *Because of linearity, the superposition principle is applicable. This states that due to $x_1(t) ⇒ y_1(t)$ and $x_2(t) ⇒ y_2(t)$ the following mapping also necessarily holds: | |
| + | :$$x_1(t) + x_2(t) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y_1(t) + y_2(t).$$ | ||
| + | *The system is »'''time-invariant'''«. This means that an input signal shifted by $\tau$ results in the same output signal, but this is also delayed by $\tau$: | ||
| + | :$$x(t - \tau) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y(t -\tau)\hspace{0.4cm}{\rm if} \hspace{0.4cm}x(t )\hspace{0.2cm}\Rightarrow \hspace{0.1cm} y(t).$$ | ||
| + | :Time-varying systems are discussed in the book [[Mobile_Communications|»Mobile Communications«]]. | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Please note:}$ | |
| − | $ | + | If all the conditions listed here are fulfilled, one deals with a »'''linear time-invariant system'''«, abbreviated $\rm LTI$ system.}} |
| − | |||
| − | |||
| + | ==Frequency response – Transfer function== | ||
| + | <br> | ||
| + | We assume an LTI system whose input and output spectra $X(f)$ and $Y(f)$ are known or can be derived from the time signals $x(t)$ and $y(t)$ via [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»Fourier transform«]]. | ||
| − | + | [[File:EN_LZI_T_1_1_S4.png|right|frame|Definition of the frequency response|class=fit]] | |
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ | ||
| + | The behaviour of a system is described in the frequency domain by the »'''frequency response'''«: | ||
| + | :$$H(f) = \frac{Y(f)}{X(f)}= \frac{ {\rm response\:function} }{ {\rm cause\:function} }.$$ | ||
| + | Other terms for $H(f)$ are »system function« and »transfer function«. }} | ||
| − | |||
| − | |||
| − | = | + | {{GraueBox|TEXT= |
| − | + | $\text{Example 2:}$ | |
| − | + | The signal $x(t)$ with real spectrum $X(f)$ $($blue curve$)$ is applied to the input of an LTI system. | |
| − | + | [[File:P_ID778__LZI_T_1_1_S4b_neu.png |right|frame|Input spectrum, output spectrum and frequency response|class=fit]] | |
| − | + | The measured output spectrum $Y(f)$ – marked red in the graph – | |
| − | + | *is larger than $X(f)$ at frequencies lower than $2 \ \rm kHz$, | |
| − | |||
| − | |||
| − | |||
| − | $ | ||
| − | |||
| − | |||
| − | + | *has a steeper slope in the region around $2 \ \rm kHz$, and | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | [[File: | + | *above $2.8 \ \rm kHz$ the signal $y(t)$ has no spectral components. |
| + | |||
| + | |||
| + | The green circles mark some measuring points of the frequency response $H(f) = Y(f)/X(f)$ which is real, too. | ||
| + | #At low frequencies it holds $H(f)>1$: In this range the LTI system has an amplifying effect. | ||
| + | #The frequency roll-off of $H(f)$ is similar to that of $Y(f)$ but not identical.}} | ||
| + | |||
| + | ==Properties of the frequency response== | ||
| + | <br> | ||
| + | The frequency response $H(f)$ is a central variable in the description of communication systems. | ||
| + | |||
| + | Some properties of this important system characteristic are listed below: | ||
| + | *The frequency response describes the LTI system on its own. It can be calculated, for example, from the linear components of an electrical network. With a different input signal $x(t)$ and a correspondingly different output signal $y(t)$ the result is exactly the same frequency response $H(f)$. | ||
| + | *The frequency response can have a "unit". For example, if one considers the voltage curve $u(t)$ as cause and the current $i(t)$ as effect for a one-port, the frequency response $H(f) = I(f)/U(f)$ has the unit $\rm A/V$. $I(f)$ and $U(f)$ are the Fourier transforms of $i(t)$ and $u(t)$, respectively. | ||
| + | *In the following we only consider »'''two-port networks'''« or so-called »'''quadripoles'''«. Moreover, without loss of generality, we usually assume that $x(t)$ and $y(t)$ are voltages, respectively. In this case $H(f)$ is always dimensionless. | ||
| + | *Since the spectra $X(f)$ and $Y(f)$ are generally complex, the frequency response $H(f)$ is also a complex function. The magnitude $|H(f)|$ is called the »'''amplitude response'''« or the "magnitude frequency response". | ||
| + | *This is also often represented in logarithmic form and called the "attenuation curve" or "gain curve": | ||
| + | :$$a(f) = - \ln |H(f)| = - 20 \cdot \lg |H(f)|.$$ | ||
| + | *Depending on whether the first form with the natural logarithm or the second with the decadic logarithm is used, the pseudo-unit "neper" $\rm (Np)$ or "decibel" $\rm (dB)$ must be added. | ||
| + | *The »'''phase response'''« can be calculated from $H(f)$ in the following way: | ||
| + | :$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in\hspace{0.1cm}radian \hspace{0.1cm}(rad)}.$$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Thus, the total frequency response can also be represented as follows}$: | ||
| + | :$$H(f) = \vert H(f)\vert \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm} \cdot\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{ - {\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$}} | ||
| + | |||
| + | ==Low-pass, high-pass, band-pass and band-stop filters== | ||
| + | <br> | ||
| + | [[File:EN_LZI_T_1_1_S6.png|right|frame|Left: Low-pass and high-pass; cut-off frequency $f_{\rm G}$ $($German: Grenzfrequenz ⇒ $\rm G)$ ,<br>Right: Band-pass; lower cut-off frequency $f_{\rm U}$, upper cut-off frequency $f_{\rm O}$|class=fit]] | ||
| + | According to the amplitude response $|H(f)|$ one distinguishes between | ||
| + | |||
| + | *»'''Low-pass filters'''«: Signal components tend to be more attenuated with increasing frequency. | ||
| + | *»'''High-pass filters'''«: Here, high-frequency signal components are attenuated less than low-frequency ones. A direct signal $($that is, a signal component with the frequency $f = 0)$ cannot be transmitted via a high-pass filter. | ||
| + | *»'''Band-pass filters'''«: There is a preferred frequency called the center frequency $f_{\rm M}$. The further away the frequency of a signal component is from $f_{\rm M}$, the more it will be attenuated. | ||
| + | *»'''Band-stop filters'''«: This is the counterpart to the band-pass filter and it is $|H(f_{\rm M})| ≈ 0$. However, very low-frequency and very high-frequency signal components are let pass. | ||
| + | |||
| + | |||
| + | The graph shows on the left the amplitude responses of the filter types "low-pass" $\rm (LP)$ and "high-pass" $\rm (HP)$, and an the right "band-pass" $\rm (BP)$. | ||
| + | |||
| + | In the sketch also shown are the »'''cut-off frequencies'''«. These denote 3dB cut-off frequencies here, for example, according to the following definition. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | The »'''3 dB cut-off frequency'''« of a low-pass filter specifies the frequency $f_{\rm G}$, for which holds: | ||
| + | :$$\vert H(f = f_{\rm G})\vert = {1}/{\sqrt{2} } \cdot \vert H(f = 0)\vert \hspace{0.5cm}\Rightarrow\hspace{0.5cm} \vert H(f = f_{\rm G})\vert^2 = {1}/{2} \cdot \vert H(f = 0) \vert^2.$$}} | ||
| + | |||
| + | |||
| + | #Note that there are also a number of other definitions for the cut-off frequency. | ||
| + | #These can be found in the section [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#General_remarks|»General Remarks«]] in the chapter »Some Low-Pass Functions in Systems Theory«. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Test signals for measuring the frequency response== |
| − | + | <br> | |
| − | $$H(f) = \frac{Y(f)}{X(f)}.$$ | + | For measuring the frequency response $H(f)$ any input signal $x(t)$ with spectrum $X(f)$  is suitable,  as long as $X(f)$ has no zeros (in the range of interest). By measuring the output spectrum $Y(f)$ the frequency response can thus be determined in a simple way: |
| − | + | :$$H(f) = \frac{Y(f)}{X(f)}.$$ | |
| − | * | + | In particular,  the following input signals are suitable: |
| − | : | + | *'''»Dirac delta function'''« $x(t) = K · δ(t)$ ⇒ spectrum $X(f) = K$: |
| − | * | + | :Thus, the frequency response by magnitude and phase is of the same shape as the output spectrum $Y(f)$ and it holds $H(f) = 1/K · Y(f)$. <br>If one approximates the Dirac delta function by a narrow rectangle of equal area $K$, then $H(f)$ must be corrected by means of a ${\rm sin}(x)/x$–function. |
| − | : | + | *'''»Dirac comb'''« – the infinite sum of equally weighted Dirac delta functions at the time interval $T_{\rm A}$: |
| − | * | + | :This leads according to the chapter [[Signal_Representation/Discrete-Time_Signal_Representation#Dirac_comb_in_time_and_frequency_domain|»Discrete-Time Signal Representation«]] to a Dirac comb in the frequency domain with distance $f_{\rm A} =1/T_{\rm A}$. This allows a discrete frequency measurement of $H(f)$ with the spectral samples spaced $f_{\rm A}$. |
| − | : | + | *'''»Harmonic oscillation'''« $x(t) = A_x · \cos (2πf_0t - φ_x)$ ⇒ Dirac-shaped spectrum at $\pm f_0$: |
| − | $$H(f_0) = \frac{Y(f_0)}{X(f_0)} = \frac{A_y}{A_x}\cdot{\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} (\varphi_x - \varphi_y)}.$$ | + | :The output signal $y(t) = A_y · \cos(2πf_0t - φ_y)$ is an oscillation of the same frequency $f_0$. The frequency response for $f_0 \gt 0$ is: |
| − | : | + | :$$H(f_0) = \frac{Y(f_0)}{X(f_0)} = \frac{A_y}{A_x}\cdot{\rm e}^{\hspace{0.05cm} {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} (\varphi_x - \varphi_y)}.$$ |
| + | :To determine the total frequency response $H(f)$ an infinite number of measurements at different frequencies $f_0$ are required. | ||
| + | |||
| + | |||
| + | |||
| + | ==Exercises for the chapter== | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_1.1:_Simple_Filter_Functions| Exercise 1.1: Simple Filter Functions]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.1Z:_Low-Pass_Filter_of_1st_and_2nd_Order|Exercise 1.1Z: Low-Pass Filter of 1st and 2nd Order]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.2:_Coaxial_Cable|Exercise 1.2: Coaxial Cable]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.2Z:_Measurement_of_the_Frequency_Response|Exercise 1.2Z: Measurement of the Frequency Response]] | ||
| + | |||
| + | |||
{{Display}} | {{Display}} | ||
Latest revision as of 18:50, 1 November 2023
- [[Linear and Time Invariant Systems/{{{Vorherige Seite}}} | Previous page]]
- [[Linear and Time Invariant Systems/{{{Vorherige Seite}}} | Previous page]]
Contents
- 1 # OVERVIEW OF THE FIRST MAIN CHAPTER #
- 2 The cause-and-effect principle
- 3 Application in Communications Engineering
- 4 Prerequisites for the application of Systems Theory
- 5 Frequency response – Transfer function
- 6 Properties of the frequency response
- 7 Low-pass, high-pass, band-pass and band-stop filters
- 8 Test signals for measuring the frequency response
- 9 Exercises for the chapter
# OVERVIEW OF THE FIRST MAIN CHAPTER #
- In the book »Signal Representation« you were familiarized with the mathematical description of deterministic signals in the time and frequency domain.
- The second book »Linear Time-Invariant Systems« now describes what changes a signal or its spectrum undergoes through a transmission system and how these changes can be captured mathematically.
- In the first chapter, the basics of the so-called »Systems Theory« are mentioned, which allows a uniform and simple description of such systems. We start with the system description in the frequency domain with the partial aspects listed above.
$\text{Please note:}$
- The »system« can be a simple circuit as well as a complete, highly complicated transmission system with a multitude of components.
- Here it is only assumed that the system has the two properties »linear« and »time-invariant«.
The cause-and-effect principle
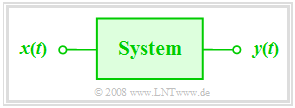
We always consider here the simple model outlined on the right. This arrangement is to be interpreted as follows:
- The focus is on the so-called »system«, which is largely abstracted in its function ⇒ »black box«. Nothing is known in detail about the realization of the system.
- The time-dependent input $x(t)$ acting on this system is also referred to as the »cause function« in the following.
- At the system output, the »effect function« $y(t)$ appears as the system response to the input function $x(t)$.
$\text{Please note:}$
- The »system« can generally be of any kind and is not limited to communications technology alone. In fact, attempts are also made in other fields of science, such as the natural sciences, economics and business administration, sociology and political science, to capture and describe causal relationships between different variables by means of the cause-and-effect principle.
- However, the methods used for these phenomenological systems theories differ significantly from the approach in Communications Engineering, which is outlined in this first main chapter of the present book »Linear Time-Invariant Systems«.
Application in Communications Engineering
The cause-and-effect principle can be applied in Communications Engineering, for example to describe one-port circuits which are also reffered to as one-ports. Here, one can consider the current curve $i(t)$ as a cause function and the voltage $u(t)$ as an effect function. By observing the I/U relationships, conclusions can be drawn about the properties of the actually unknown one-port.
In Germany, $\text{Karl Küpfmüller}$ introduced the term »Systems Theory« for the first time in 1949. He considers it as a method for describing complex causal relationships in natural sciences and technology, based on a spectral transformation, e.g. the »Fourier transform«.
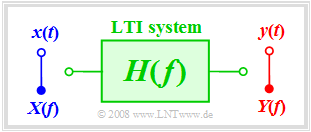
A transmission system can entirely be described in terms of systems theory . Here
- the »cause function« is the input signal $x(t)$ or its spectrum $X(f)$,
- the »effect function« is the output signal $y(t)$ or its spectrum $Y(f)$.
Also in the following graphs, input variables are mostly drawn in blue, output variables in red and system variables in green.
$\text{Example 1:}$
(1) For example, if the »system« describes a given linear electric circuit, then given a known input signal $x(t)$ the output signal $y(t)$ can be predicted with the help of "Systems Theory".
(2) A second task of "Systems Theory" is to classify the transmission system by measuring $y(t)$ knowing $x(t)$ but without knowing the system in detail.
(3) If $x(t)$ describes, for instance, the voice of a caller in Hamburg and $y(t)$ the recording of an answering machine in Munich, then the »transmission system« consists of the following components:
- Microphone – telephone – electrical line – signal converter $($electrical-optical$)$ – fiber optic cable – optical amplifier – signal converter $($optical-electrical$)$ – receiver filter $($for equalization and noise limitation$)$ – . . . . . . – electromagnetic transducer.
Prerequisites for the application of Systems Theory
The model of a transmission system given above holds generally and independently of the boundary conditions. However, the application of systems theory requires some additional limiting preconditions.
Unless explicitly stated otherwise, the following shall always apply:
- Both $x(t)$ and $y(t)$ are »deterministic« signals. Otherwise, one must proceed according to the chapter »Stochastic System Theory«.
- The system is »linear«. This can be seen, for example, from the fact that a harmonic oscillation $x(t)$ at the input also results in a harmonic oscillation $y(t)$ of the same frequency at the output:
- $$x(t) = A_x \cdot \cos(\omega_0 \hspace{0.05cm}t - \varphi_x)\hspace{0.2cm}\Rightarrow \hspace{0.2cm} y(t) = A_y \cdot\cos(\omega_0 \hspace{0.05cm}t - \varphi_y).$$
- New frequencies do not arise. Only amplitude and phase of the harmonic oscillation can be changed. Nonlinear systems are treated in the chapter »Nonlinear Distortions«.
- Because of linearity, the superposition principle is applicable. This states that due to $x_1(t) ⇒ y_1(t)$ and $x_2(t) ⇒ y_2(t)$ the following mapping also necessarily holds:
- $$x_1(t) + x_2(t) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y_1(t) + y_2(t).$$
- The system is »time-invariant«. This means that an input signal shifted by $\tau$ results in the same output signal, but this is also delayed by $\tau$:
- $$x(t - \tau) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y(t -\tau)\hspace{0.4cm}{\rm if} \hspace{0.4cm}x(t )\hspace{0.2cm}\Rightarrow \hspace{0.1cm} y(t).$$
- Time-varying systems are discussed in the book »Mobile Communications«.
$\text{Please note:}$ If all the conditions listed here are fulfilled, one deals with a »linear time-invariant system«, abbreviated $\rm LTI$ system.
Frequency response – Transfer function
We assume an LTI system whose input and output spectra $X(f)$ and $Y(f)$ are known or can be derived from the time signals $x(t)$ and $y(t)$ via »Fourier transform«.
$\text{Definition:}$ The behaviour of a system is described in the frequency domain by the »frequency response«:
- $$H(f) = \frac{Y(f)}{X(f)}= \frac{ {\rm response\:function} }{ {\rm cause\:function} }.$$
Other terms for $H(f)$ are »system function« and »transfer function«.
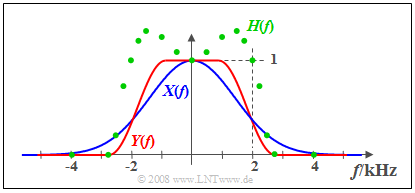
$\text{Example 2:}$ The signal $x(t)$ with real spectrum $X(f)$ $($blue curve$)$ is applied to the input of an LTI system.
The measured output spectrum $Y(f)$ – marked red in the graph –
- is larger than $X(f)$ at frequencies lower than $2 \ \rm kHz$,
- has a steeper slope in the region around $2 \ \rm kHz$, and
- above $2.8 \ \rm kHz$ the signal $y(t)$ has no spectral components.
The green circles mark some measuring points of the frequency response $H(f) = Y(f)/X(f)$ which is real, too.
- At low frequencies it holds $H(f)>1$: In this range the LTI system has an amplifying effect.
- The frequency roll-off of $H(f)$ is similar to that of $Y(f)$ but not identical.
Properties of the frequency response
The frequency response $H(f)$ is a central variable in the description of communication systems.
Some properties of this important system characteristic are listed below:
- The frequency response describes the LTI system on its own. It can be calculated, for example, from the linear components of an electrical network. With a different input signal $x(t)$ and a correspondingly different output signal $y(t)$ the result is exactly the same frequency response $H(f)$.
- The frequency response can have a "unit". For example, if one considers the voltage curve $u(t)$ as cause and the current $i(t)$ as effect for a one-port, the frequency response $H(f) = I(f)/U(f)$ has the unit $\rm A/V$. $I(f)$ and $U(f)$ are the Fourier transforms of $i(t)$ and $u(t)$, respectively.
- In the following we only consider »two-port networks« or so-called »quadripoles«. Moreover, without loss of generality, we usually assume that $x(t)$ and $y(t)$ are voltages, respectively. In this case $H(f)$ is always dimensionless.
- Since the spectra $X(f)$ and $Y(f)$ are generally complex, the frequency response $H(f)$ is also a complex function. The magnitude $|H(f)|$ is called the »amplitude response« or the "magnitude frequency response".
- This is also often represented in logarithmic form and called the "attenuation curve" or "gain curve":
- $$a(f) = - \ln |H(f)| = - 20 \cdot \lg |H(f)|.$$
- Depending on whether the first form with the natural logarithm or the second with the decadic logarithm is used, the pseudo-unit "neper" $\rm (Np)$ or "decibel" $\rm (dB)$ must be added.
- The »phase response« can be calculated from $H(f)$ in the following way:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in\hspace{0.1cm}radian \hspace{0.1cm}(rad)}.$$
$\text{Thus, the total frequency response can also be represented as follows}$:
- $$H(f) = \vert H(f)\vert \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm} \cdot\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{ - {\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
Low-pass, high-pass, band-pass and band-stop filters
According to the amplitude response $|H(f)|$ one distinguishes between
- »Low-pass filters«: Signal components tend to be more attenuated with increasing frequency.
- »High-pass filters«: Here, high-frequency signal components are attenuated less than low-frequency ones. A direct signal $($that is, a signal component with the frequency $f = 0)$ cannot be transmitted via a high-pass filter.
- »Band-pass filters«: There is a preferred frequency called the center frequency $f_{\rm M}$. The further away the frequency of a signal component is from $f_{\rm M}$, the more it will be attenuated.
- »Band-stop filters«: This is the counterpart to the band-pass filter and it is $|H(f_{\rm M})| ≈ 0$. However, very low-frequency and very high-frequency signal components are let pass.
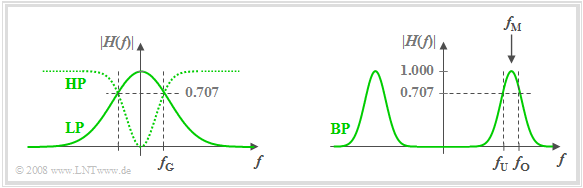
The graph shows on the left the amplitude responses of the filter types "low-pass" $\rm (LP)$ and "high-pass" $\rm (HP)$, and an the right "band-pass" $\rm (BP)$.
In the sketch also shown are the »cut-off frequencies«. These denote 3dB cut-off frequencies here, for example, according to the following definition.
$\text{Definition:}$ The »3 dB cut-off frequency« of a low-pass filter specifies the frequency $f_{\rm G}$, for which holds:
- $$\vert H(f = f_{\rm G})\vert = {1}/{\sqrt{2} } \cdot \vert H(f = 0)\vert \hspace{0.5cm}\Rightarrow\hspace{0.5cm} \vert H(f = f_{\rm G})\vert^2 = {1}/{2} \cdot \vert H(f = 0) \vert^2.$$
- Note that there are also a number of other definitions for the cut-off frequency.
- These can be found in the section »General Remarks« in the chapter »Some Low-Pass Functions in Systems Theory«.
Test signals for measuring the frequency response
For measuring the frequency response $H(f)$ any input signal $x(t)$ with spectrum $X(f)$  is suitable,  as long as $X(f)$ has no zeros (in the range of interest). By measuring the output spectrum $Y(f)$ the frequency response can thus be determined in a simple way:
- $$H(f) = \frac{Y(f)}{X(f)}.$$
In particular,  the following input signals are suitable:
- »Dirac delta function« $x(t) = K · δ(t)$ ⇒ spectrum $X(f) = K$:
- Thus, the frequency response by magnitude and phase is of the same shape as the output spectrum $Y(f)$ and it holds $H(f) = 1/K · Y(f)$.
If one approximates the Dirac delta function by a narrow rectangle of equal area $K$, then $H(f)$ must be corrected by means of a ${\rm sin}(x)/x$–function.
- »Dirac comb« – the infinite sum of equally weighted Dirac delta functions at the time interval $T_{\rm A}$:
- This leads according to the chapter »Discrete-Time Signal Representation« to a Dirac comb in the frequency domain with distance $f_{\rm A} =1/T_{\rm A}$. This allows a discrete frequency measurement of $H(f)$ with the spectral samples spaced $f_{\rm A}$.
- »Harmonic oscillation« $x(t) = A_x · \cos (2πf_0t - φ_x)$ ⇒ Dirac-shaped spectrum at $\pm f_0$:
- The output signal $y(t) = A_y · \cos(2πf_0t - φ_y)$ is an oscillation of the same frequency $f_0$. The frequency response for $f_0 \gt 0$ is:
- $$H(f_0) = \frac{Y(f_0)}{X(f_0)} = \frac{A_y}{A_x}\cdot{\rm e}^{\hspace{0.05cm} {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} (\varphi_x - \varphi_y)}.$$
- To determine the total frequency response $H(f)$ an infinite number of measurements at different frequencies $f_0$ are required.
Exercises for the chapter
Exercise 1.1: Simple Filter Functions
Exercise 1.1Z: Low-Pass Filter of 1st and 2nd Order
Exercise 1.2Z: Measurement of the Frequency Response