Difference between revisions of "Signal Representation/Differences and Similarities of Low-Pass and Band-Pass Signals"
m (Text replacement - "lowpass" to "low-pass") |
|||
| (26 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Band-Pass Signals |
|Vorherige Seite=The Convolution Theorem and Operation | |Vorherige Seite=The Convolution Theorem and Operation | ||
|Nächste Seite=Analytical Signal and Its Spectral Function | |Nächste Seite=Analytical Signal and Its Spectral Function | ||
| Line 8: | Line 8: | ||
== # OVERVIEW OF THE FOURTH MAIN CHAPTER # == | == # OVERVIEW OF THE FOURTH MAIN CHAPTER # == | ||
<br> | <br> | ||
| − | In the third main chapter | + | In the third main chapter ⇒ [[Signal_Representation|»Aperiodic Signals – Pulses«]] mostly "low-pass signals" were assumed ⇒ those signals whose spectral functions lie in the range around the frequency $f = 0$. Particularly in optical transmission and in radio transmission systems - but not only in these - the transmitted signals are in the range around a carrier frequency $f_{\rm T}$. Such signals are called »'''band-pass signals'''«. |
| − | All principles of the Fourier transform and the inverse Fourier transform described in the last chapter apply to | + | All principles of the Fourier transform and the inverse Fourier transform described in the last chapter apply to band-pass signals in the same way. Besides there are some special features of band-pass signals, whose observance can lead to a simpler description. |
This chapter contains in detail: | This chapter contains in detail: | ||
| − | + | #The enumeration of »differences and similarities« of low-pass and band-pass signals, | |
| − | + | #the »synthesis of band-pass signals« from the »equivalent low-pass signal«, | |
| − | + | #the equivalent low-pass signal in the time and frequency domain, and finally | |
| − | + | #the representation of the »analytical signal« and of the »equivalent low-pass signal« in the complex plane. | |
| − | ==Motivation of | + | ==Motivation of band-pass signals for Communications Engineering== |
<br> | <br> | ||
| − | In the previous chapters of this book, only signals whose spectra lie in a narrow range around the frequency $f = 0$ | + | In the previous chapters of this book, only signals have been considered whose spectra lie in a narrow range around the frequency $f = 0$. Examples are analog speech, music and image signals, which all – despite their different bandwidths – can be described as »low-pass signals«. |
| − | If you want to transmit such a low-pass signal to a spatially distant sink, the signal may have to be converted to another frequency position. There can be several reasons for this: | + | If you want to transmit such a low-pass signal to a spatially distant sink, the signal may have to be converted to another frequency position. |
| − | *Often the transmission channel is unsuitable for the direct transmission of the source signal in the original frequency band, because this band contains frequencies that are unfavorable for it. Only by a frequency shift by means of a so-called | + | |
| − | *A single transmission channel can be used for the simultaneous transmission of several signals, if they are modulated with different carrier frequencies at the transmitting end. This method is called [[Modulation_Methods/ | + | There can be several reasons for this: |
| − | *The transmission quality can be improved compared to the simplest analog method[[Modulation_Methods/Zweiseitenband-Amplitudenmodulation|Amplitude Modulation]] at the expense of a larger bandwidth and thus a higher | + | *Often the transmission channel is unsuitable for the direct transmission of the source signal in the original frequency band, because this band contains frequencies that are unfavorable for it. Only by a frequency shift by means of a so-called »modulator« a transmission is made possible. |
| + | |||
| + | *A single transmission channel can be used for the simultaneous transmission of several signals, if they are modulated with different carrier frequencies at the transmitting end. This method is called [[Modulation_Methods/Objectives_of_Modulation_and_Demodulation#Channel_bundling_.E2.80.93_Frequency_Division_Multiplexing|»Frequency Division Multiple Access»]] $\text{(FDMA)}$. | ||
| + | |||
| + | *The transmission quality can be improved compared to the simplest analog method [[Modulation_Methods/Zweiseitenband-Amplitudenmodulation|»Amplitude Modulation«]] $\text{(AM)}$ at the expense of a larger bandwidth and thus a higher »signal-to-noise ratio» $\text{(SNR)}$ can be achieved. Examples are the analog [[Modulation_Methods/Frequenzmodulation_(FM)|»Frequency Modulation«]] $\text{(FM)}$ and the digital [[Modulation_Methods/Pulse_Code_Modulation|»Pulse Code Modulation«]] $\text{(PCM)}$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Remember:}$ The transmitted signals of many transmission methods are | + | $\text{Remember:}$ The transmitted signals of many transmission methods are »band-pass signals«.}} |
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 1 : To classify signals with respect to »low-pass« and »band-pass«}$ | ||
| + | '''(a)''' Speech and music are low-pass signals with a bandwidth of $\text{20 kHz}$ $($at very good quality$)$. Since a radio transmission is only possible from $\approx \text{100 kHz}$, a conversion is needed to carrier frequencies between | ||
| + | *$\text{0.525 ... 1.61 MHz}$ $($medium wave broadcasting, amplitude modulation, channel spacing $\text{9 kHz})$, | ||
| − | + | *$\text{87.5 ... 108 MHz}$ $($radio on FM, frequency modulation, channel spacing $\text{300 kHz})$. | |
| − | |||
| − | |||
| − | '''( | + | '''(b)''' TV image signals have a larger bandwidth, e.g. $\text{5 MHz}$. Here, as well, a frequency band shift occurs before the sound and image transmission due to carrier frequencies between |
| − | *$\text{ | + | *$\text{41 ... 68 / 174 ... 230 MHz}$ $($television, VHF band, channel spacing $\text{7 MHz})$, |
| − | |||
| − | |||
| + | *$\text{470 ... 850 MHz}$ $($television, UHF band, channel spacing $\text{8 MHz})$. | ||
| − | |||
| − | |||
| − | |||
| − | '''(c)''' With | + | '''(c)''' With »GSM mobile radio« the carrier frequencies in the D-band are $\text{900 MHz}$ and in the E-band $\text{1800 MHz}$. |
| − | '''(d)''' With | + | '''(d)''' With »optical communication« the electrical signals are converted into light, i.e. to frequencies $\text{200 THz ... 350 THz}$ ⇒ wavelengths: $\text{1.55 µm ... 0.85 µm}$.}} |
| − | ==Properties of | + | ==Properties of band-pass signals== |
<br> | <br> | ||
| − | + | In this section – without claiming to be complete – some characteristics of band-pass signals $x_{\rm BP}(t)$ are compiled and compared to low-pass signals $x_{\rm TP}(t)$, because of "low-pass" ⇒ German: "Tiefpass" ⇒ "$\rm TP$". We start from the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ according to the following sketch. | |
| − | [[File:P_ID679__Sig_T_4_1_S2a_neu.png| | + | Regarding the graphic is to be remarked: |
| + | [[File:P_ID679__Sig_T_4_1_S2a_neu.png|right|frame|Low-pass and band-pass spectrum]] | ||
| − | + | #The triangular shape of the displayed spectra is to be understood schematically and is only to mark the occupied frequency band. | |
| − | + | #So it should not be concluded that all frequencies within the band are actually occupied and that all spectral functions increase linearly with frequency $f$. | |
| − | + | #The corresponding time functions $x_{\rm TP}(t)$ and $x_{\rm BP}(t)$ are real. This means that according to the [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|»Assignment Theorem«]] the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ each have an even real part and an odd imaginary part $($related to the frequency $f = 0)$. | |
| − | + | #As bandwidth $B_{\rm TP}$ or $B_{\rm BP}$ for both low-pass and band-pass we refer to the occupied frequency band at positive frequencies $($in the graph: solid lines$)$. | |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Example 2:}$ An example with discrete spectral lines follows. The left graph shows the spectrum $Q(f)$ of the | + | $\text{Example 2:}$ An example with discrete spectral lines follows. |
| + | [[File:P_ID698__Sig_T_4_1_S2b_neu.png|right|frame|Example of a low-pass spectrum (left) and of a band-pass spectrum (right)]] | ||
| + | |||
| + | The left graph shows the spectrum $Q(f)$ of the source signal | ||
| − | :$$q(t) = 3\hspace{0.05cm}{\rm V} + 4\hspace{0.05cm}{\rm V} \cdot \cos (2 \pi \cdot 3\hspace{0.05cm}{\rm kHz} \cdot t) + 2\hspace{0.05cm}{\rm V} \cdot \sin (2 \pi \cdot 4\hspace{0.05cm}{\rm kHz} \cdot t). $$ | + | :$$q(t) = 3\hspace{0.05cm}{\rm V} + 4\hspace{0.05cm}{\rm V} \cdot \cos (2 \pi \hspace{-0.05cm} \cdot\hspace{-0.05cm} 3\hspace{0.05cm}{\rm kHz} \cdot t) + 2\hspace{0.05cm}{\rm V} \cdot \sin (2 \pi\hspace{-0.05cm} \cdot\hspace{-0.05cm} 4\hspace{0.05cm}{\rm kHz} \cdot t). $$ |
The discrete spectral lines of the real part ⇒ ${\rm Re}\big[Q(f)\big]$ are shown in blue and those of the imaginary part ⇒ ${\rm Im}\big[Q(f)\big]$ in red. | The discrete spectral lines of the real part ⇒ ${\rm Re}\big[Q(f)\big]$ are shown in blue and those of the imaginary part ⇒ ${\rm Im}\big[Q(f)\big]$ in red. | ||
| − | |||
| − | On the right | + | ⇒ On the right you see the spectrum $S(f)$ after »Single–sideband Amplitude Modulation« $\text{(SSB-AM)}$ with carrier frequency $f_{\rm T} = 100 \,\text{kHz}$. |
| − | |||
| − | |||
| − | |||
| + | A description of this special transmission system can be found in chapter [[Modulation_Methods/Hüllkurvendemodulation|»Envelope Demodulation»]] of the book »Modulation Methods«. | ||
| + | *According to this description, $q(t)$ is uniquely a low-pass signal and $s(t)$ is a band-pass signal. The bandwidths are $B_{\rm TP} = B_{\rm BP} = 4 \,\text{kHz}$. | ||
| + | *The signals $q(t)$ and $s(t)$ are real, since both $Q(f)$ and $S(f)$ have an even real and an odd imaginary part. | ||
| + | *If the DC component $(3 \,\text{V})$ would be missing in the source signal, one would sensibly $q(t)$ still call it "low-pass" with bandwidth $B_{\rm TP} = 4 \,\text{kHz}$. | ||
| + | *But without knowledge of the task, one could interpret $q(t)$ then also as a "band-pass signal" with bandwidth $B_{\rm BP} = 1 \,\text{kHz}$. | ||
| + | This example shows that there is no clear mathematical distinction between low-pass and band-pass signals.}} | ||
| − | + | ==Description of a band-pass signal with low-pass signals== | |
| − | |||
| − | ==Description of a | ||
<br> | <br> | ||
We consider two low-pass spectra $X_1(f)$ and $X_2(f)$ with the bandwidths $B_1$ and $B_2$ corresponding to the left graph. | We consider two low-pass spectra $X_1(f)$ and $X_2(f)$ with the bandwidths $B_1$ and $B_2$ corresponding to the left graph. | ||
| − | [[File:P_ID684__Sig_T_4_1_S3a.png| | + | [[File:P_ID684__Sig_T_4_1_S3a.png|right|frame|Generation of a band-pass spectrum from two low-pass spectra]] |
You can see from this diagram: | You can see from this diagram: | ||
| − | *If $X_1(f)$ and $X_2(f)$ up to a frequency $f_{12}$ | + | *If $X_1(f)$ and $X_2(f)$ are identical up to a frequency $f_{12}$, the difference describes a band-pass spectrum with bandwidth $B_{\rm BP} = B_1 - f_{12}$. |
| + | |||
| + | *According to the graph on the right, the following then applies: | ||
:$$X_{\rm BP}(f) = X_1(f) -X_2(f).$$ | :$$X_{\rm BP}(f) = X_1(f) -X_2(f).$$ | ||
| − | *Due to the linearity of the Fourier transform, the time function associated with the | + | *Due to the linearity of the Fourier transform, the time function associated with the band-pass spectrum $X_{\rm BP}(f)$ is valid: |
:$$x_{\rm BP}(t) = x_1(t) - x_2(t).$$ | :$$x_{\rm BP}(t) = x_1(t) - x_2(t).$$ | ||
| − | *It generally follows from the Fourier | + | *It generally follows from the Fourier transform that the integral over the time function is equal to the spectral value at $f = 0$. |
| + | |||
| + | * Consequently, this integral is always zero for every band-pass signal: | ||
:$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | :$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | ||
d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$ | d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$ | ||
| Line 104: | Line 115: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 3:}$ | $\text{Example 3:}$ | ||
| − | The red curves in the two graphs show the | + | The red curves in the two graphs show the band-pass spectrum $X_{\rm BP}(f)$ and the corresponding time function |
:$$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm | :$$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm | ||
| − | V} \cdot {\rm | + | V} \cdot {\rm sinc} ( 10 \hspace{0.05cm}{\rm kHz} \cdot t) |
| − | \cdot {\rm | + | \cdot {\rm sinc} ( 2 \hspace{0.05cm}{\rm kHz} \cdot t) - |
| − | 2\hspace{0.05cm}{\rm V} \cdot {\rm | + | 2\hspace{0.05cm}{\rm V} \cdot {\rm sinc} ( 2 |
\hspace{0.05cm}{\rm kHz} \cdot t).$$ | \hspace{0.05cm}{\rm kHz} \cdot t).$$ | ||
| − | [[File:EN_Sig_T_4_1_S3a.png| | + | [[File:EN_Sig_T_4_1_S3a.png|right|frame|Low-pass and band-pass spectrum and their signals]] |
| − | Also shown are | + | Also shown are two low-pass spectra and signals. You can see from these diagrams: |
| − | *The blue-dotted curve in the left graph represents the trapezoidal spectrum $X_1(f)$ where the equivalent bandwidth $\Delta f_1= 10 \,\text{kHz}$ and the rolloff factor $r_1 = 0.2$ | + | *The blue-dotted curve in the left graph represents the trapezoidal spectrum $X_1(f)$ where the equivalent bandwidth is $\Delta f_1= 10 \,\text{kHz}$ and the rolloff factor $r_1 = 0.2$. |
| − | *The blue-dotted curve in the right graphic shows the corresponding low-pass | + | |
| + | *The blue-dotted curve in the right graphic shows the corresponding low-pass signal $x_1(t)$. The signal value at $t = 0$ corresponds to the blue trapezoidal area of the spectrum $X_1(f)$: | ||
:$$x_1(t = 0) = 10 \,\text{V}.$$ | :$$x_1(t = 0) = 10 \,\text{V}.$$ | ||
| − | *The green curve applies to the rectangular spectrum $X_2(f)$ with the equivalent bandwidth $\Delta f_2= 2 \,\text{kHz}$. The corresponding time signal $x_2(t)$ | + | *The green curve applies to the rectangular spectrum $X_2(f)$ with the equivalent bandwidth $\Delta f_2= 2 \,\text{kHz}$. The corresponding time signal $x_2(t)$ is $\rm sinc$-shaped. It holds: |
:$$x_2(t = 0) = 2 \,\text{V}.$$ | :$$x_2(t = 0) = 2 \,\text{V}.$$ | ||
| − | The red curve for the | + | *The red curve for the band-pass signal is the difference between the blue and green curve, both on the left and the right. Accordingly: |
:$$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$ | :$$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$ | ||
| − | :$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | + | :$$\Rightarrow \ \int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm |
d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$}} | d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$}} | ||
| − | == | + | ==Band-pass signal synthesis from the equivalent low-pass signal== |
<br> | <br> | ||
We consider a low-pass signal $x_{\rm TP}(t)$ with spectrum $X_{\rm TP}(f)$ according to the left sketch. | We consider a low-pass signal $x_{\rm TP}(t)$ with spectrum $X_{\rm TP}(f)$ according to the left sketch. | ||
| − | If this signal is multiplied by a (dimensionless) harmonic oscillation | + | [[File:P_ID2724__Sig_T_4_1_S4a.png|center|frame|Band-pass spectrum is obtained by shifting a low-pass spectrum on both sides]] |
| + | |||
| + | *If this signal is multiplied by a $($dimensionless$)$ »harmonic oscillation« | ||
:$$z(t) = {\cos} ( 2\pi \cdot f_{\rm T} \cdot | :$$z(t) = {\cos} ( 2\pi \cdot f_{\rm T} \cdot | ||
| Line 136: | Line 150: | ||
\delta (f - f_{\rm T})+ {1}/{2}\cdot \delta (f + f_{\rm T}),$$ | \delta (f - f_{\rm T})+ {1}/{2}\cdot \delta (f + f_{\rm T}),$$ | ||
| − | the convolution theorem for the spectrum of the signal $x_{\rm BP}(t) = x_{\rm TP}(t) | + | :the convolution theorem for the spectrum of the signal yields $x_{\rm BP}(t) = x_{\rm TP}(t) \cdot z(t)$: |
:$$X_{\rm BP}(f) = X_{\rm TP}(f)\star Z(f) = {1}/{2}\cdot X_{\rm | :$$X_{\rm BP}(f) = X_{\rm TP}(f)\star Z(f) = {1}/{2}\cdot X_{\rm | ||
TP} (f - f_{\rm T})+ {1}/{2}\cdot X_{\rm TP}(f + f_{\rm T}).$$ | TP} (f - f_{\rm T})+ {1}/{2}\cdot X_{\rm TP}(f + f_{\rm T}).$$ | ||
| − | Here it is considered that the [[Signal_Representation/The_Convolution_Theorem_and_Operation| | + | *Here it is considered that the [[Signal_Representation/The_Convolution_Theorem_and_Operation|»convolution«]] of the spectral function $X_{\rm TP}(f)$ with the frequency-shifted Dirac delta $\delta (f - f_\rm {T})$ yields the same spectral function $X_{\rm TP}(f-f_\rm {T})$ shifted to the right by $f_\rm {T}$ . |
| − | + | *From spectral function on the right you can clearly see that | |
| − | |||
| − | From the right | ||
:$$x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T} | :$$x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T} | ||
\cdot t)$$ | \cdot t)$$ | ||
| − | is a | + | :is a band-pass signal: |
| − | For example, this principle is applied to the [[Modulation_Methods/Zweiseitenband-Amplitudenmodulation|amplitude modulation without carrier]],which is discussed thoroughly in the book & | + | *The envelope of $x_{\rm BP}(t)$ is given by the magnitude of $|x_{\rm TP}(t)|$. |
| + | |||
| + | *For example, this principle is applied to the [[Modulation_Methods/Zweiseitenband-Amplitudenmodulation|»amplitude modulation without carrier«]], which is discussed thoroughly in the book» »Modulation Methods«. | ||
| + | |||
| + | |||
| + | You can further see from the above graphic: | ||
| + | #The spectrum $X_{\rm BP}(f)$ has the same form in the range around the carrier frequency $f_{\rm T}$ as $X_{\rm TP}(f)$ in the range around $f = 0$, but the band-pass spectrum is attenuated with respect to the low-pass spectrum by the factor $2$. | ||
| + | #Since $X_{\rm TP}(f)$ relative to $f = 0$ has an even real and an odd imaginary part, the band-pass spectrum $X_{\rm BP}(f)$ has the same symmetry properties – but now relative to the carrier frequency $f_{\rm T}$. | ||
| + | #$X_{\rm BP}(f)$ also has parts at negative frequencies. Since the corresponding signal $x_{\rm BP}(t)$ is real according to the above equation, $X_{\rm BP}(f)$ must also have an even real and an odd imaginary part with respect to the frequency $f = 0$. | ||
| + | #The bandwidth of the band-pass signal is twice that of the low-pass signal: $B_{\rm BP} = 2 \cdot B_{\rm TP}$. Prerequisite for the validity of this statement is that the carrier frequency $f_{\rm T}$ is at least twice as large than the maximum frequency $(B_{\rm TP})$ of the signal $x_{\rm TP}(t)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 4:}$ A low-pass signal has discrete spectral components at $f_1 = 1\,\text{ kHz}, \,f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ and $f_4 = 4\,\text{ kHz}$: | $\text{Example 4:}$ A low-pass signal has discrete spectral components at $f_1 = 1\,\text{ kHz}, \,f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ and $f_4 = 4\,\text{ kHz}$: | ||
| − | :$$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + | + | [[File:P_ID687__Sig_T_4_1_S4b.png|right|frame|DSB-AM signal with two different carrier frequencies]] |
| + | |||
| + | :$$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + $$ | ||
| + | :$$\hspace{1.5cm}+ \ 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + | ||
120^{ \circ}) +0.14\cdot {\cos} ( \omega_4 \hspace{0.05cm} t -40^{ | 120^{ \circ}) +0.14\cdot {\cos} ( \omega_4 \hspace{0.05cm} t -40^{ | ||
\circ}).$$ | \circ}).$$ | ||
| Line 167: | Line 186: | ||
The corresponding spectrum $X_{\rm TP}(f)$ is complex because of the non-zero phase positions. | The corresponding spectrum $X_{\rm TP}(f)$ is complex because of the non-zero phase positions. | ||
| − | + | *If one multiplies the $($blue$)$  signal $x_{\rm TP}(t)$ with a cosine signal of amplitude $1$ and frequency $f_{\rm T} = 20 \,\text{kHz}$, the (red) band-pass signal is obtained according to the upper graphic. | |
| − | + | ||
| − | *If one multiplies $x_{\rm TP}(t)$ with a cosine signal of amplitude $1$ and frequency $f_{\rm T} = 20 \,\text{kHz}$, the | + | *The lower sketch applies to the band-pass signal with carrier frequency $f_{\rm T} = 100 \,\text{kHz}$. |
| − | *The lower sketch applies to the | + | |
| − | *In both illustrations the | + | *In both illustrations the time curves $\pm \vert x_{\rm TP}(t) \vert $ can be recognized as the envelope of the band-pass signals $x_{\rm BP}(t)$. |
| − | + | The topic of this chapter is covered in the (German language) learning video [[Eigenschaften_von_Tiefpass-_und_Bandpasssignalen_(Lernvideo)|»Eigenschaften von Tiefpass- und Bandpass-Signalen«]] ⇒ "Properties of low-pass and band-pass signals".}} | |
| − | |||
| − | |||
| − | |||
| Line 184: | Line 200: | ||
==Exercises for the Chapter== | ==Exercises for the Chapter== | ||
<br> | <br> | ||
| − | [[Aufgaben:Exercise 4.1: | + | [[Aufgaben:Exercise 4.1: Low-Pass and Band-Pass Signals|Exercise 4.1: Low-Pass and Band-Pass Signals]] |
| − | [[Aufgaben:Exercise 4.1Z: | + | [[Aufgaben:Exercise 4.1Z: High-Pass System|Exercise 4.1Z: High-Pass System]] |
| − | [[Aufgaben:Exercise 4.2: Rectangular-Shaped Spectra|Exercise 4.2: Rectangular | + | [[Aufgaben:Exercise 4.2: Rectangular-Shaped Spectra|Exercise 4.2: Rectangular Spectra]] |
[[Aufgaben:Exercise 4.2Z: Multiplication with a Sine Signal|Exercise 4.2Z: Multiplication with a Sine Signal]] | [[Aufgaben:Exercise 4.2Z: Multiplication with a Sine Signal|Exercise 4.2Z: Multiplication with a Sine Signal]] | ||
Latest revision as of 16:37, 19 June 2023
Contents
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
In the third main chapter ⇒ »Aperiodic Signals – Pulses« mostly "low-pass signals" were assumed ⇒ those signals whose spectral functions lie in the range around the frequency $f = 0$. Particularly in optical transmission and in radio transmission systems - but not only in these - the transmitted signals are in the range around a carrier frequency $f_{\rm T}$. Such signals are called »band-pass signals«.
All principles of the Fourier transform and the inverse Fourier transform described in the last chapter apply to band-pass signals in the same way. Besides there are some special features of band-pass signals, whose observance can lead to a simpler description.
This chapter contains in detail:
- The enumeration of »differences and similarities« of low-pass and band-pass signals,
- the »synthesis of band-pass signals« from the »equivalent low-pass signal«,
- the equivalent low-pass signal in the time and frequency domain, and finally
- the representation of the »analytical signal« and of the »equivalent low-pass signal« in the complex plane.
Motivation of band-pass signals for Communications Engineering
In the previous chapters of this book, only signals have been considered whose spectra lie in a narrow range around the frequency $f = 0$. Examples are analog speech, music and image signals, which all – despite their different bandwidths – can be described as »low-pass signals«.
If you want to transmit such a low-pass signal to a spatially distant sink, the signal may have to be converted to another frequency position.
There can be several reasons for this:
- Often the transmission channel is unsuitable for the direct transmission of the source signal in the original frequency band, because this band contains frequencies that are unfavorable for it. Only by a frequency shift by means of a so-called »modulator« a transmission is made possible.
- A single transmission channel can be used for the simultaneous transmission of several signals, if they are modulated with different carrier frequencies at the transmitting end. This method is called »Frequency Division Multiple Access» $\text{(FDMA)}$.
- The transmission quality can be improved compared to the simplest analog method »Amplitude Modulation« $\text{(AM)}$ at the expense of a larger bandwidth and thus a higher »signal-to-noise ratio» $\text{(SNR)}$ can be achieved. Examples are the analog »Frequency Modulation« $\text{(FM)}$ and the digital »Pulse Code Modulation« $\text{(PCM)}$.
$\text{Remember:}$ The transmitted signals of many transmission methods are »band-pass signals«.
$\text{Example 1 : To classify signals with respect to »low-pass« and »band-pass«}$
(a) Speech and music are low-pass signals with a bandwidth of $\text{20 kHz}$ $($at very good quality$)$. Since a radio transmission is only possible from $\approx \text{100 kHz}$, a conversion is needed to carrier frequencies between
- $\text{0.525 ... 1.61 MHz}$ $($medium wave broadcasting, amplitude modulation, channel spacing $\text{9 kHz})$,
- $\text{87.5 ... 108 MHz}$ $($radio on FM, frequency modulation, channel spacing $\text{300 kHz})$.
(b) TV image signals have a larger bandwidth, e.g. $\text{5 MHz}$. Here, as well, a frequency band shift occurs before the sound and image transmission due to carrier frequencies between
- $\text{41 ... 68 / 174 ... 230 MHz}$ $($television, VHF band, channel spacing $\text{7 MHz})$,
- $\text{470 ... 850 MHz}$ $($television, UHF band, channel spacing $\text{8 MHz})$.
(c) With »GSM mobile radio« the carrier frequencies in the D-band are $\text{900 MHz}$ and in the E-band $\text{1800 MHz}$.
(d) With »optical communication« the electrical signals are converted into light, i.e. to frequencies $\text{200 THz ... 350 THz}$ ⇒ wavelengths: $\text{1.55 µm ... 0.85 µm}$.
Properties of band-pass signals
In this section – without claiming to be complete – some characteristics of band-pass signals $x_{\rm BP}(t)$ are compiled and compared to low-pass signals $x_{\rm TP}(t)$, because of "low-pass" ⇒ German: "Tiefpass" ⇒ "$\rm TP$". We start from the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ according to the following sketch.
Regarding the graphic is to be remarked:
- The triangular shape of the displayed spectra is to be understood schematically and is only to mark the occupied frequency band.
- So it should not be concluded that all frequencies within the band are actually occupied and that all spectral functions increase linearly with frequency $f$.
- The corresponding time functions $x_{\rm TP}(t)$ and $x_{\rm BP}(t)$ are real. This means that according to the »Assignment Theorem« the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ each have an even real part and an odd imaginary part $($related to the frequency $f = 0)$.
- As bandwidth $B_{\rm TP}$ or $B_{\rm BP}$ for both low-pass and band-pass we refer to the occupied frequency band at positive frequencies $($in the graph: solid lines$)$.
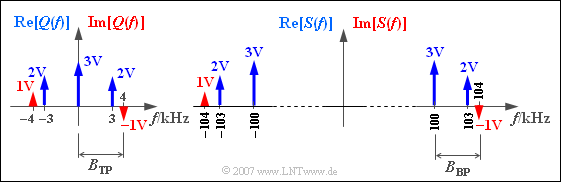
$\text{Example 2:}$ An example with discrete spectral lines follows.
The left graph shows the spectrum $Q(f)$ of the source signal
- $$q(t) = 3\hspace{0.05cm}{\rm V} + 4\hspace{0.05cm}{\rm V} \cdot \cos (2 \pi \hspace{-0.05cm} \cdot\hspace{-0.05cm} 3\hspace{0.05cm}{\rm kHz} \cdot t) + 2\hspace{0.05cm}{\rm V} \cdot \sin (2 \pi\hspace{-0.05cm} \cdot\hspace{-0.05cm} 4\hspace{0.05cm}{\rm kHz} \cdot t). $$
The discrete spectral lines of the real part ⇒ ${\rm Re}\big[Q(f)\big]$ are shown in blue and those of the imaginary part ⇒ ${\rm Im}\big[Q(f)\big]$ in red.
⇒ On the right you see the spectrum $S(f)$ after »Single–sideband Amplitude Modulation« $\text{(SSB-AM)}$ with carrier frequency $f_{\rm T} = 100 \,\text{kHz}$.
A description of this special transmission system can be found in chapter »Envelope Demodulation» of the book »Modulation Methods«.
- According to this description, $q(t)$ is uniquely a low-pass signal and $s(t)$ is a band-pass signal. The bandwidths are $B_{\rm TP} = B_{\rm BP} = 4 \,\text{kHz}$.
- The signals $q(t)$ and $s(t)$ are real, since both $Q(f)$ and $S(f)$ have an even real and an odd imaginary part.
- If the DC component $(3 \,\text{V})$ would be missing in the source signal, one would sensibly $q(t)$ still call it "low-pass" with bandwidth $B_{\rm TP} = 4 \,\text{kHz}$.
- But without knowledge of the task, one could interpret $q(t)$ then also as a "band-pass signal" with bandwidth $B_{\rm BP} = 1 \,\text{kHz}$.
This example shows that there is no clear mathematical distinction between low-pass and band-pass signals.
Description of a band-pass signal with low-pass signals
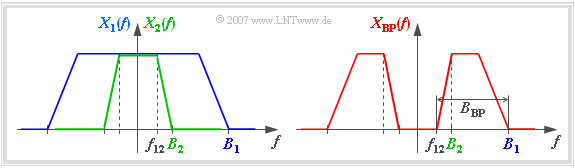
We consider two low-pass spectra $X_1(f)$ and $X_2(f)$ with the bandwidths $B_1$ and $B_2$ corresponding to the left graph.
You can see from this diagram:
- If $X_1(f)$ and $X_2(f)$ are identical up to a frequency $f_{12}$, the difference describes a band-pass spectrum with bandwidth $B_{\rm BP} = B_1 - f_{12}$.
- According to the graph on the right, the following then applies:
- $$X_{\rm BP}(f) = X_1(f) -X_2(f).$$
- Due to the linearity of the Fourier transform, the time function associated with the band-pass spectrum $X_{\rm BP}(f)$ is valid:
- $$x_{\rm BP}(t) = x_1(t) - x_2(t).$$
- It generally follows from the Fourier transform that the integral over the time function is equal to the spectral value at $f = 0$.
- Consequently, this integral is always zero for every band-pass signal:
- $$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$
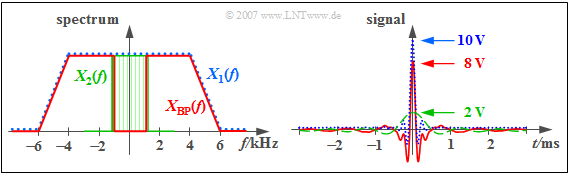
$\text{Example 3:}$ The red curves in the two graphs show the band-pass spectrum $X_{\rm BP}(f)$ and the corresponding time function
- $$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm V} \cdot {\rm sinc} ( 10 \hspace{0.05cm}{\rm kHz} \cdot t) \cdot {\rm sinc} ( 2 \hspace{0.05cm}{\rm kHz} \cdot t) - 2\hspace{0.05cm}{\rm V} \cdot {\rm sinc} ( 2 \hspace{0.05cm}{\rm kHz} \cdot t).$$
Also shown are two low-pass spectra and signals. You can see from these diagrams:
- The blue-dotted curve in the left graph represents the trapezoidal spectrum $X_1(f)$ where the equivalent bandwidth is $\Delta f_1= 10 \,\text{kHz}$ and the rolloff factor $r_1 = 0.2$.
- The blue-dotted curve in the right graphic shows the corresponding low-pass signal $x_1(t)$. The signal value at $t = 0$ corresponds to the blue trapezoidal area of the spectrum $X_1(f)$:
- $$x_1(t = 0) = 10 \,\text{V}.$$
- The green curve applies to the rectangular spectrum $X_2(f)$ with the equivalent bandwidth $\Delta f_2= 2 \,\text{kHz}$. The corresponding time signal $x_2(t)$ is $\rm sinc$-shaped. It holds:
- $$x_2(t = 0) = 2 \,\text{V}.$$
- The red curve for the band-pass signal is the difference between the blue and green curve, both on the left and the right. Accordingly:
- $$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$
- $$\Rightarrow \ \int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$
Band-pass signal synthesis from the equivalent low-pass signal
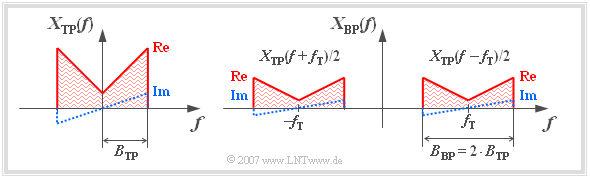
We consider a low-pass signal $x_{\rm TP}(t)$ with spectrum $X_{\rm TP}(f)$ according to the left sketch.
- If this signal is multiplied by a $($dimensionless$)$ »harmonic oscillation«
- $$z(t) = {\cos} ( 2\pi \cdot f_{\rm T} \cdot t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.15cm} Z(f) = {1}/{2}\cdot \delta (f - f_{\rm T})+ {1}/{2}\cdot \delta (f + f_{\rm T}),$$
- the convolution theorem for the spectrum of the signal yields $x_{\rm BP}(t) = x_{\rm TP}(t) \cdot z(t)$:
- $$X_{\rm BP}(f) = X_{\rm TP}(f)\star Z(f) = {1}/{2}\cdot X_{\rm TP} (f - f_{\rm T})+ {1}/{2}\cdot X_{\rm TP}(f + f_{\rm T}).$$
- Here it is considered that the »convolution« of the spectral function $X_{\rm TP}(f)$ with the frequency-shifted Dirac delta $\delta (f - f_\rm {T})$ yields the same spectral function $X_{\rm TP}(f-f_\rm {T})$ shifted to the right by $f_\rm {T}$ .
- From spectral function on the right you can clearly see that
- $$x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T} \cdot t)$$
- is a band-pass signal:
- The envelope of $x_{\rm BP}(t)$ is given by the magnitude of $|x_{\rm TP}(t)|$.
- For example, this principle is applied to the »amplitude modulation without carrier«, which is discussed thoroughly in the book» »Modulation Methods«.
You can further see from the above graphic:
- The spectrum $X_{\rm BP}(f)$ has the same form in the range around the carrier frequency $f_{\rm T}$ as $X_{\rm TP}(f)$ in the range around $f = 0$, but the band-pass spectrum is attenuated with respect to the low-pass spectrum by the factor $2$.
- Since $X_{\rm TP}(f)$ relative to $f = 0$ has an even real and an odd imaginary part, the band-pass spectrum $X_{\rm BP}(f)$ has the same symmetry properties – but now relative to the carrier frequency $f_{\rm T}$.
- $X_{\rm BP}(f)$ also has parts at negative frequencies. Since the corresponding signal $x_{\rm BP}(t)$ is real according to the above equation, $X_{\rm BP}(f)$ must also have an even real and an odd imaginary part with respect to the frequency $f = 0$.
- The bandwidth of the band-pass signal is twice that of the low-pass signal: $B_{\rm BP} = 2 \cdot B_{\rm TP}$. Prerequisite for the validity of this statement is that the carrier frequency $f_{\rm T}$ is at least twice as large than the maximum frequency $(B_{\rm TP})$ of the signal $x_{\rm TP}(t)$.
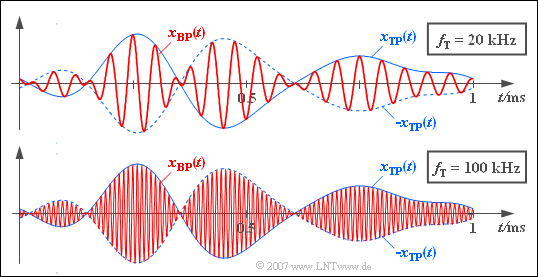
$\text{Example 4:}$ A low-pass signal has discrete spectral components at $f_1 = 1\,\text{ kHz}, \,f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ and $f_4 = 4\,\text{ kHz}$:
- $$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + $$
- $$\hspace{1.5cm}+ \ 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + 120^{ \circ}) +0.14\cdot {\cos} ( \omega_4 \hspace{0.05cm} t -40^{ \circ}).$$
The corresponding spectrum $X_{\rm TP}(f)$ is complex because of the non-zero phase positions.
- If one multiplies the $($blue$)$  signal $x_{\rm TP}(t)$ with a cosine signal of amplitude $1$ and frequency $f_{\rm T} = 20 \,\text{kHz}$, the (red) band-pass signal is obtained according to the upper graphic.
- The lower sketch applies to the band-pass signal with carrier frequency $f_{\rm T} = 100 \,\text{kHz}$.
- In both illustrations the time curves $\pm \vert x_{\rm TP}(t) \vert $ can be recognized as the envelope of the band-pass signals $x_{\rm BP}(t)$.
The topic of this chapter is covered in the (German language) learning video »Eigenschaften von Tiefpass- und Bandpass-Signalen« ⇒ "Properties of low-pass and band-pass signals".
Exercises for the Chapter
Exercise 4.1: Low-Pass and Band-Pass Signals
Exercise 4.1Z: High-Pass System
Exercise 4.2: Rectangular Spectra
Exercise 4.2Z: Multiplication with a Sine Signal