Difference between revisions of "Theory of Stochastic Signals/Matched Filter"
| (56 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Filtering of Stochastic Signals |
|Vorherige Seite=Erzeugung vorgegebener AKF-Eigenschaften | |Vorherige Seite=Erzeugung vorgegebener AKF-Eigenschaften | ||
|Nächste Seite=Wiener–Kolmogorow–Filter | |Nächste Seite=Wiener–Kolmogorow–Filter | ||
}} | }} | ||
| − | == | + | ==Optimization criterion of the matched filter== |
| − | + | <br> | |
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ The »'''matched filter'''« – also called "correlation filter" – is used to prove the signal existence. | ||
| + | [[File:EN_Sto_T_5_4_S1_neu2.png |right|frame| Block diagram of the "matched filter receiver"]] | ||
| + | The »'''matched filter receiver'''« can decide with the greatest possible certainty – in other words: with maximum SNR – whether or not a pulse $g(t)$ disturbed by additive white noise $n(t)$ is present. | ||
| + | |||
| + | To derive the "matched filter receiver", consider the block diagram on the right. }} | ||
| − | |||
| + | The following conditions apply to the individual components: | ||
| + | *Let the useful component $g(t)$ of the received signal $r(t)=g(t)+n(t)$ be pulse-shaped and thus "energy-limited". | ||
| + | *That means: The integral over $\big [g(t)\big ]^2$ from $–∞$ to $+∞$ yields the finite value $E_g$. | ||
| + | *Let the noise signal $n(t)$ be "white Gaussian noise" with (one–sided) noise power density $N_0$. | ||
| + | *The signal $d(t)$ is additively composed of two components: The component $d_{\rm S}(t)$ is due to the "$\rm S$"ignal $g(t)$, the component $d_{\rm N}(t)$ is due to the "$\rm N$"oise $n(t)$. | ||
| + | *The receiver, consisting of a linear filter ⇒ frequency response $H_{\rm MF}(f)$ and the "decision", is to be dimensioned <br>so that the instantaneous S/N ratio at the output is maximized: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$ | ||
| + | *Here, $σ_d^2$ denotes the variance ("power") of the signal $d_{\rm N}(t)$, and $T_{\rm D}$ denotes the (suitably chosen) "detection time". | ||
| − | + | ==Matched filter optimization== | |
| − | + | <br> | |
| − | + | Let be given an energy-limited useful signal $g(t)$ with the corresponding spectrum $G(f)$. | |
| − | + | *Thus, the filter output signal at detection time $T_{\rm D}$ for any filter with impulse response $h(t)$ and frequency response $H(f) =\mathcal{ F}\{h(t)\}$ can be written as follows <br>(ignoring noise ⇒ subscript $\rm S$ for "signal"): | |
| − | + | :$$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$ | |
| − | $$\rho _d ( {T_{\rm D} } ) = \frac{ { | + | *The "noise component" $d_{\rm N}(t)$ of the filter output signal (subscript $\rm N$ for "noise") stems solely from the white noise $n(t)$ at the input of the receiver. For its variance (power) applies independently of the detection time $T_{\rm D}$: |
| − | + | :$$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$ | |
| + | *Thus, the optimization problem at hand is: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$ | ||
| − | = | + | {{BlaueBox|TEXT= |
| − | + | $\text{Here first without proof:}$ One can show that this quotient becomes largest for the following frequency response $H(f)$: | |
| − | $$ | + | :$$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$ |
| − | + | *Thus, for the signal–to–noise power ratio at the matched filter output $($independent of the dimensionally constant $K_{\rm MF})$, we obtain: | |
| − | + | :$$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } }.$$ | |
| − | |||
| − | |||
| − | |||
| − | $$ | ||
| − | |||
| − | $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } | ||
| − | |||
| − | |||
| − | |||
| + | * $E_g$ denotes the energy of the input pulse, which can be calculated using [https://en.wikipedia.org/wiki/Parseval%27s_theorem $\text{Parseval's theorem}$] in both the time and frequency domains: | ||
| + | :$$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$}} | ||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = | + | $\text{Example 1:}$ A rectangular pulse $g(t)$ with amplitude $\rm 1\hspace{0.05cm}V$, duration $0.5\hspace{0.05cm} \rm ms$ and unknown position is to be found in a noisy environment. |
| + | *Thus the pulse energy $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$. | ||
| + | *Let the noise power density be $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$. | ||
| + | |||
| + | |||
| + | The best result ⇒ the »'''maximum S/N ratio'''« is obtained with the matched filter: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = | ||
\frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 | \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm} | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
| − | 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$ | + | 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$}} |
| − | |||
| − | + | The matched filter criterion given above is now derived step by step. If you are not interested in this, please skip to the next section [[Theory_of_Stochastic_Signals/Matched_Filter#Interpretation_of_the_matched_filter|"Interpretation of the matched filter"]]. | |
| − | = | + | {{BlaueBox|TEXT= |
| − | + | $\text{Derivation of the matched filter criterion:}$ | |
| + | $(1)$ The Schwarz inequality with the two (generally complex) functions $A(f)$ and $B(f)$: | ||
| + | :$$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$ | ||
| + | $(2)$ We now apply this equation to the signal–to–noise ratio: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$ | ||
| + | $(3)$ Thus, with $A(f) = G(f)$ and $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ the following bound is obtained: | ||
| + | :$$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$ | ||
| + | $(4)$ We now tentatively set for the filter frequency response: | ||
| + | :$$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$ | ||
| + | $(5)$ Then, from the above equation $(2)$, we obtain the following result: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$ | ||
| − | + | $\text{This means:}$ | |
| − | + | *With the approach $(4)$ for the matched filter $H_{\rm MF}(f)$, the maximum possible value is indeed obtained in the above estimation. | |
| − | + | *No other filter $H(f) ≠ H_{\rm MF}(f)$ can achieve a higher signal–to–noise power ratio. | |
| − | + | *The matched filter is optimal with respect to the maximization criterion on which it is based. | |
| − | + | <div align="right">'''q.e.d.'''</div> | |
| − | + | }} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We refer here to the HTML5/JavaScript applet [[Applets:Matched_Filter_Properties|"Matched Filter Properties"]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Interpretation of the matched filter== | ||
| + | <br> | ||
| + | In the last section, the frequency response of the matched filter was derived as follows: | ||
| + | :$$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$ | ||
| + | By [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|$\text{Fourier inverse transformation}$]] the corresponding impulse response is obtained: | ||
| + | :$$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$ | ||
| − | + | These two functions can be interpreted as follows: | |
| − | * | + | *The "matched filter" is matched by the term $G^{\star}(f)$ to the spectrum of the pulse $g(t)$ which is to be found – hence its name. |
| − | * | + | *The "constant" $K_{\rm MF}$ is necessary for dimensional reasons. |
| − | * | + | *If $g(t)$ is a voltage pulse, this constant has the unit "Hz/V". The frequency response $H_{\rm MF} (f)$ is therefore dimensionless. |
| − | * | + | *The "impulse response" $h_{\rm MF}(t)$ results from the useful signal $g(t)$ by mirroring ⇒ from $g(t)$ becomes $g(–t)$ $]$ as well as a shift by $T_{\rm D}$ to the right. |
| − | * | + | *The "earliest detection time" $T_{\rm D}$ follows for realizable systems from the condition $h_{\rm MF}(t < 0)\equiv 0$ $($"causality", see book [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Causal_systems|"Linear and Time-Invariant Systems"]]$)$. |
| − | $$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$ | + | *The "useful component" $d_{\rm S} (t)$ of the filter output signal is equal in shape to the [[Digital_Signal_Transmission/Basics_of_Coded_Transmission#ACF_calculation_of_a_digital_signal|$\text{energy auto-correlation function}$]] $\varphi^{^{\bullet} }_{g} (t )$ and shifted with respect to it by $T_{\rm D}$. It holds: |
| − | + | :$$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$ | |
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Please note:}$ | ||
| + | For an energy-limited signal $g(t)$, one can only specify the »'''energy ACF'''«: | ||
| + | :$$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$ | ||
| + | Compared to the ACF definition of a power-limited signal $x(t)$, viz. | ||
| + | :$$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$ | ||
| + | the division by the measurement duration $T_{\rm M}$ and the boundary transition $T_{\rm M} → ∞$ are omitted in the calculation of the energy ACF.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ We assume that the rectangular pulse is between $\rm 2\hspace{0.08cm}ms$ and $\rm 2.5\hspace{0.08cm}ms$ and the detection time $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ is desired. | ||
| − | + | Under these conditions: | |
| − | + | *The matched filter impulse response $h_{\rm MF}(t)$ must be constant in the range from $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ to $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$. | |
| − | * | + | *For $t < t_1$ as well as for $t > t_2$ it must not have any components. |
| − | * | + | *The magnitude frequency response $\vert H_{\rm MF}(f)\vert$ is $\rm sinc$–shaped here. |
| + | *The magnitude of the impulse response $h_{\rm MF}(t)$ is not important for the S/N ratio, because $\rho _d ( {T_{\rm D} } )$ is independent of $K_{\rm MF}$.}} | ||
| − | + | We refer here to the HTML5/JavaScript applet [[Applets:Matched_Filter_Properties|"Matched Filter Properties"]]. | |
| − | |||
| − | |||
| − | + | ==Generalized matched filter for the case of colored interference== | |
| + | <br> | ||
| + | In the derivations of this section, white noise has always been assumed so far. Now the following question shall be clarified:<br> How should the receiver filter $H(f) = H_{\rm MF}(f)$ be designed in the presence of »'''colored interference'''« $n(t)$ so that the signal to noise power ratio is maximized? | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{To explain some terminology:}$ The term "interference" is somewhat more general than "noise." | ||
| + | *Rather, noise is a subset of all interference, which includes, for example, crosstalk from adjacent lines. | ||
| + | *We speak of (white) noise $n(t)$ only if the power-spectral density ${\it Φ}_n(f)$ is the same for all frequencies. | ||
| + | *If this is not satisfied, we refer to $n(t)$ as "colored interference".}} | ||
| − | + | <br> | |
| + | [[File:EN_Sto_T_5_4_S4.png |right|frame| Matched filter with colored resp. white noise]] | ||
| + | The top diagram shows the block diagram for deriving the matched filter $H_{\rm MF}(f)$ in the presence of colored interference $n(t)$, denoted by the power-spectral density ${\it Φ}_n(f) ≠\text{ const}$. All other conditions stated so far for this section still apply. | ||
| + | |||
| + | Regarding the modified model according to the diagram below, note: | ||
| + | *The colored interference signal $n(t)$ with power-spectral density ${\it Φ}_n(f)$ can be modeled – at least mentally – by a "white" noise source $n_{\rm WN}(t)$ with the constant (two-sided) noise power density $N_0/2$ and a shape filter with frequency response $H_{\rm N}(f)$: | ||
| + | :$${\it{\Phi} }_n \left( f \right) = { {N_{\rm 0} } }/{\rm 2} \cdot \left| {H_{\rm N} \left( f \right)} \right|^{\rm 2} .$$ | ||
| − | + | *Since implementation aspects are not considered here, $H_{\rm N}(f)$ is assumed to be real (for simplicity). The phase response of $H_{\rm N}(f)$ is not important for what follows. | |
| − | * | + | *In this representation the shape filter $H_{\rm N}(f)$ is shifted to the right side of the interference addition. To obtain a model which is also equivalent with respect to the useful signal $d_{\rm S}(t)$, the shape filter in the useful signal branch is compensated by the inverse filter $H_{\rm N}(f)^{–1}$. |
| − | |||
| − | |||
| − | |||
| − | *In | ||
| − | |||
| − | |||
| + | Using this modified model, the matched filter is now derived for the case of colored interference. If $H_{\rm N}(f)$ has no zero, which shall be assumed for the following, this arrangement is identical to the block diagram above. | ||
| − | + | White noise $n_{\rm WN}(t)$ is now present at the interference addition point. The derivation of the [[Theory_of_Stochastic_Signals/Matched_Filter#Matched_filter_optimization|$\text{matched filter optimization in the presence of white noise}$]] can be easily adapted to the current problem by considering the following: | |
| + | *Instead of the actual useful signal $g(t)$, consider the signal $g_{\rm WN}(t)$ before the interference addition. | ||
| + | *The corresponding spectral function is: $G_{\rm WN}(f) = G(f)/H_{\rm N}(f)$. | ||
| + | *Instead of $H_{\rm MF}(f)$, the resulting frequency response ${H_{\rm MF} }' (f) = H_{\rm N}(f) · H_{\rm MF}$ is now to be substituted to the right of the interference addition point. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Conclusion:}$ | |
| − | |||
| + | '''(1)''' | ||
| + | For the »'''matched filter in the presence of colored interference'''« we get: | ||
| + | :$${H_{\rm MF} }\hspace{0.01cm}' (f) = H_{\rm N} (f) \cdot H_{\rm MF} (f) = K_{\rm MF} \cdot G_{\rm WN} ^ {\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm MF} (f) = K_{\rm MF} \cdot \frac{ {G^{\star} (f)} }{ {\left\vert {H_{\rm N} (f)} \right\vert^2 } } \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$ | ||
| + | '''(2)''' Thus, the »'''signal-to-interference power ratio'''« before the decider is maximum: | ||
| + | :$$\rho _{d,\ \max } ( {T_{\rm D} } ) = \frac{1}{ {N_0 /2} }\int_{ - \infty }^{ + \infty } {\left\vert{G_{\rm WN} (f)} \right\vert^2 }\, {\rm{d} }f = \int_{ - \infty }^{ + \infty } \frac{\left \vert G(f) \right\vert^2 }{ {\it{\Phi _n {\rm (f)} } } } \,{\rm{d} }f.$$ | ||
| + | '''(3)''' The "white noise" case is included in this more general equation for ${\it Φ}_n(f) = N_0/2$. | ||
| + | '''(4)''' However, all equations given here lead to meaningful results, which can also be used in practice, '''in case of colored interference only if the energy spectrum $\vert G(f)\vert ^2$ of the useful signal decays asymptotically faster than the interference power-spectral density ${\it Φ}_n(f)$'''.}} | ||
| − | + | ==Exercises for the chapter== | |
| − | + | <br> | |
| − | + | [[Aufgaben:Exercise_5.7:_Rectangular_Matched_Filter|Exercise 5.7: Rectangular Matched Filter]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Aufgaben:Exercise_5.7Z:_Matched_Filter_-_All_Gaussian|Exercise 5.7Z: Matched Filter - All Gaussian]] | ||
| − | + | [[Aufgaben:Exercise_5.8:_Matched_Filter_for_Colored_Interference|Exercise 5.8: Matched Filter for Colored Interference]] | |
| + | [[Aufgaben:Exercise_5.8Z:_Matched_Filter_for_Rectangular_PSD|Exercise 5.8Z: Matched Filter for Rectangular PSD]] | ||
| − | |||
{{Display}} | {{Display}} | ||
Latest revision as of 11:22, 22 December 2022
Contents
Optimization criterion of the matched filter
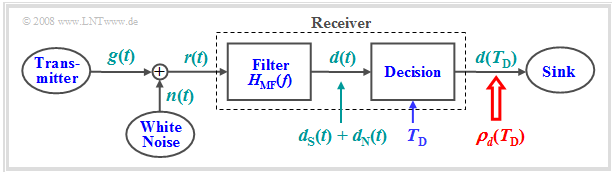
$\text{Definition:}$ The »matched filter« – also called "correlation filter" – is used to prove the signal existence.
The »matched filter receiver« can decide with the greatest possible certainty – in other words: with maximum SNR – whether or not a pulse $g(t)$ disturbed by additive white noise $n(t)$ is present.
To derive the "matched filter receiver", consider the block diagram on the right.
The following conditions apply to the individual components:
- Let the useful component $g(t)$ of the received signal $r(t)=g(t)+n(t)$ be pulse-shaped and thus "energy-limited".
- That means: The integral over $\big [g(t)\big ]^2$ from $–∞$ to $+∞$ yields the finite value $E_g$.
- Let the noise signal $n(t)$ be "white Gaussian noise" with (one–sided) noise power density $N_0$.
- The signal $d(t)$ is additively composed of two components: The component $d_{\rm S}(t)$ is due to the "$\rm S$"ignal $g(t)$, the component $d_{\rm N}(t)$ is due to the "$\rm N$"oise $n(t)$.
- The receiver, consisting of a linear filter ⇒ frequency response $H_{\rm MF}(f)$ and the "decision", is to be dimensioned
so that the instantaneous S/N ratio at the output is maximized:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$
- Here, $σ_d^2$ denotes the variance ("power") of the signal $d_{\rm N}(t)$, and $T_{\rm D}$ denotes the (suitably chosen) "detection time".
Matched filter optimization
Let be given an energy-limited useful signal $g(t)$ with the corresponding spectrum $G(f)$.
- Thus, the filter output signal at detection time $T_{\rm D}$ for any filter with impulse response $h(t)$ and frequency response $H(f) =\mathcal{ F}\{h(t)\}$ can be written as follows
(ignoring noise ⇒ subscript $\rm S$ for "signal"):
- $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$
- The "noise component" $d_{\rm N}(t)$ of the filter output signal (subscript $\rm N$ for "noise") stems solely from the white noise $n(t)$ at the input of the receiver. For its variance (power) applies independently of the detection time $T_{\rm D}$:
- $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
- Thus, the optimization problem at hand is:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$
$\text{Here first without proof:}$ One can show that this quotient becomes largest for the following frequency response $H(f)$:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$
- Thus, for the signal–to–noise power ratio at the matched filter output $($independent of the dimensionally constant $K_{\rm MF})$, we obtain:
- $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } }.$$
- $E_g$ denotes the energy of the input pulse, which can be calculated using $\text{Parseval's theorem}$ in both the time and frequency domains:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$
$\text{Example 1:}$ A rectangular pulse $g(t)$ with amplitude $\rm 1\hspace{0.05cm}V$, duration $0.5\hspace{0.05cm} \rm ms$ and unknown position is to be found in a noisy environment.
- Thus the pulse energy $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$.
- Let the noise power density be $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$.
The best result ⇒ the »maximum S/N ratio« is obtained with the matched filter:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$
The matched filter criterion given above is now derived step by step. If you are not interested in this, please skip to the next section "Interpretation of the matched filter".
$\text{Derivation of the matched filter criterion:}$
$(1)$ The Schwarz inequality with the two (generally complex) functions $A(f)$ and $B(f)$:
- $$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$
$(2)$ We now apply this equation to the signal–to–noise ratio:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$
$(3)$ Thus, with $A(f) = G(f)$ and $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ the following bound is obtained:
- $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$
$(4)$ We now tentatively set for the filter frequency response:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$
$(5)$ Then, from the above equation $(2)$, we obtain the following result:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
$\text{This means:}$
- With the approach $(4)$ for the matched filter $H_{\rm MF}(f)$, the maximum possible value is indeed obtained in the above estimation.
- No other filter $H(f) ≠ H_{\rm MF}(f)$ can achieve a higher signal–to–noise power ratio.
- The matched filter is optimal with respect to the maximization criterion on which it is based.
We refer here to the HTML5/JavaScript applet "Matched Filter Properties".
Interpretation of the matched filter
In the last section, the frequency response of the matched filter was derived as follows:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$
By $\text{Fourier inverse transformation}$ the corresponding impulse response is obtained:
- $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$
These two functions can be interpreted as follows:
- The "matched filter" is matched by the term $G^{\star}(f)$ to the spectrum of the pulse $g(t)$ which is to be found – hence its name.
- The "constant" $K_{\rm MF}$ is necessary for dimensional reasons.
- If $g(t)$ is a voltage pulse, this constant has the unit "Hz/V". The frequency response $H_{\rm MF} (f)$ is therefore dimensionless.
- The "impulse response" $h_{\rm MF}(t)$ results from the useful signal $g(t)$ by mirroring ⇒ from $g(t)$ becomes $g(–t)$ $]$ as well as a shift by $T_{\rm D}$ to the right.
- The "earliest detection time" $T_{\rm D}$ follows for realizable systems from the condition $h_{\rm MF}(t < 0)\equiv 0$ $($"causality", see book "Linear and Time-Invariant Systems"$)$.
- The "useful component" $d_{\rm S} (t)$ of the filter output signal is equal in shape to the $\text{energy auto-correlation function}$ $\varphi^{^{\bullet} }_{g} (t )$ and shifted with respect to it by $T_{\rm D}$. It holds:
- $$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$
$\text{Please note:}$ For an energy-limited signal $g(t)$, one can only specify the »energy ACF«:
- $$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$
Compared to the ACF definition of a power-limited signal $x(t)$, viz.
- $$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$
the division by the measurement duration $T_{\rm M}$ and the boundary transition $T_{\rm M} → ∞$ are omitted in the calculation of the energy ACF.
$\text{Example 2:}$ We assume that the rectangular pulse is between $\rm 2\hspace{0.08cm}ms$ and $\rm 2.5\hspace{0.08cm}ms$ and the detection time $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ is desired.
Under these conditions:
- The matched filter impulse response $h_{\rm MF}(t)$ must be constant in the range from $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ to $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$.
- For $t < t_1$ as well as for $t > t_2$ it must not have any components.
- The magnitude frequency response $\vert H_{\rm MF}(f)\vert$ is $\rm sinc$–shaped here.
- The magnitude of the impulse response $h_{\rm MF}(t)$ is not important for the S/N ratio, because $\rho _d ( {T_{\rm D} } )$ is independent of $K_{\rm MF}$.
We refer here to the HTML5/JavaScript applet "Matched Filter Properties".
Generalized matched filter for the case of colored interference
In the derivations of this section, white noise has always been assumed so far. Now the following question shall be clarified:
How should the receiver filter $H(f) = H_{\rm MF}(f)$ be designed in the presence of »colored interference« $n(t)$ so that the signal to noise power ratio is maximized?
$\text{To explain some terminology:}$ The term "interference" is somewhat more general than "noise."
- Rather, noise is a subset of all interference, which includes, for example, crosstalk from adjacent lines.
- We speak of (white) noise $n(t)$ only if the power-spectral density ${\it Φ}_n(f)$ is the same for all frequencies.
- If this is not satisfied, we refer to $n(t)$ as "colored interference".
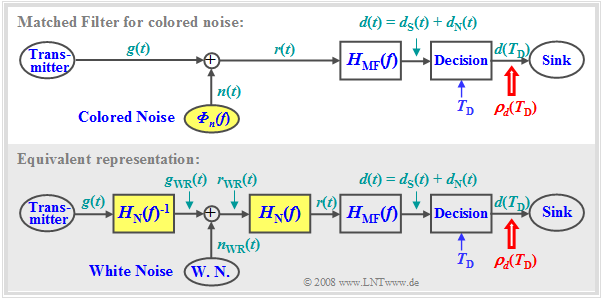
The top diagram shows the block diagram for deriving the matched filter $H_{\rm MF}(f)$ in the presence of colored interference $n(t)$, denoted by the power-spectral density ${\it Φ}_n(f) ≠\text{ const}$. All other conditions stated so far for this section still apply.
Regarding the modified model according to the diagram below, note:
- The colored interference signal $n(t)$ with power-spectral density ${\it Φ}_n(f)$ can be modeled – at least mentally – by a "white" noise source $n_{\rm WN}(t)$ with the constant (two-sided) noise power density $N_0/2$ and a shape filter with frequency response $H_{\rm N}(f)$:
- $${\it{\Phi} }_n \left( f \right) = { {N_{\rm 0} } }/{\rm 2} \cdot \left| {H_{\rm N} \left( f \right)} \right|^{\rm 2} .$$
- Since implementation aspects are not considered here, $H_{\rm N}(f)$ is assumed to be real (for simplicity). The phase response of $H_{\rm N}(f)$ is not important for what follows.
- In this representation the shape filter $H_{\rm N}(f)$ is shifted to the right side of the interference addition. To obtain a model which is also equivalent with respect to the useful signal $d_{\rm S}(t)$, the shape filter in the useful signal branch is compensated by the inverse filter $H_{\rm N}(f)^{–1}$.
Using this modified model, the matched filter is now derived for the case of colored interference. If $H_{\rm N}(f)$ has no zero, which shall be assumed for the following, this arrangement is identical to the block diagram above.
White noise $n_{\rm WN}(t)$ is now present at the interference addition point. The derivation of the $\text{matched filter optimization in the presence of white noise}$ can be easily adapted to the current problem by considering the following:
- Instead of the actual useful signal $g(t)$, consider the signal $g_{\rm WN}(t)$ before the interference addition.
- The corresponding spectral function is: $G_{\rm WN}(f) = G(f)/H_{\rm N}(f)$.
- Instead of $H_{\rm MF}(f)$, the resulting frequency response ${H_{\rm MF} }' (f) = H_{\rm N}(f) · H_{\rm MF}$ is now to be substituted to the right of the interference addition point.
$\text{Conclusion:}$
(1) For the »matched filter in the presence of colored interference« we get:
- $${H_{\rm MF} }\hspace{0.01cm}' (f) = H_{\rm N} (f) \cdot H_{\rm MF} (f) = K_{\rm MF} \cdot G_{\rm WN} ^ {\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm MF} (f) = K_{\rm MF} \cdot \frac{ {G^{\star} (f)} }{ {\left\vert {H_{\rm N} (f)} \right\vert^2 } } \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$
(2) Thus, the »signal-to-interference power ratio« before the decider is maximum:
- $$\rho _{d,\ \max } ( {T_{\rm D} } ) = \frac{1}{ {N_0 /2} }\int_{ - \infty }^{ + \infty } {\left\vert{G_{\rm WN} (f)} \right\vert^2 }\, {\rm{d} }f = \int_{ - \infty }^{ + \infty } \frac{\left \vert G(f) \right\vert^2 }{ {\it{\Phi _n {\rm (f)} } } } \,{\rm{d} }f.$$
(3) The "white noise" case is included in this more general equation for ${\it Φ}_n(f) = N_0/2$.
(4) However, all equations given here lead to meaningful results, which can also be used in practice, in case of colored interference only if the energy spectrum $\vert G(f)\vert ^2$ of the useful signal decays asymptotically faster than the interference power-spectral density ${\it Φ}_n(f)$.
Exercises for the chapter
Exercise 5.7: Rectangular Matched Filter
Exercise 5.7Z: Matched Filter - All Gaussian
Exercise 5.8: Matched Filter for Colored Interference
Exercise 5.8Z: Matched Filter for Rectangular PSD