Difference between revisions of "Digital Signal Transmission/Linear Nyquist Equalization"
| Line 8: | Line 8: | ||
== Structure of the optimal Nyquist equalizer == | == Structure of the optimal Nyquist equalizer == | ||
<br> | <br> | ||
| + | In this section we assume the following block diagram of a binary system. In this regard, it should be noted: | ||
[[File:P ID1423 Dig T 3 5 S1 version1.png|right|frame|Block diagram of the optimal Nyquist equalizer|class=fit]] | [[File:P ID1423 Dig T 3 5 S1 version1.png|right|frame|Block diagram of the optimal Nyquist equalizer|class=fit]] | ||
| − | |||
| − | |||
| − | *The | + | *The "Dirac source" provides the message to be transmitted in binary bipolar form ⇒ amplitude coefficients $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. The source is assumed to be redundancy-free. |
| − | |||
| − | |||
| − | *The | + | *The "transmission pulse shape" $g_s(t)$ is taken into account by the transmitter frequency response $H_{\rm S}(f)$. Mostly, $H_{\rm S}(f) = {\rm sinc}(f T)$ is based ⇒ NRZ rectangular transmission pulses. |
| − | *The total frequency response between | + | *In some derivations, transmitter and channel are combined by the "common frequency response" $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$. <br> |
| + | |||
| + | *The receiver filter $H_{\rm E}(f)$ is multiplicatively composed of the [[Theory_of_Stochastic_Signals/Matched_Filter|matched filter]] $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ and the [[Digital_Signal_Transmission/Linear_Nyquist_Equalization#Mode_of_action_of_the_transversal_filter|transversal filter]] $H_{\rm TF}(f)$, at least it can be split up mentally in this way. | ||
| + | |||
| + | *The total frequency response between Dirac source and threshold decision should satisfy the [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_frequency_domain| "first Nyquist condition"]]. Thus, it must hold: | ||
:$$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) | :$$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) | ||
= H_{\rm Nyq}(f) | = H_{\rm Nyq}(f) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *With this condition, there is no intersymbol interference and the maximum eye opening is obtained. Therefore, the [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission#Optimal_binary_receiver_.E2.80.93_.22Matched_Filter.22_realization|"detection SNR"]] and [[Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems#System_optimization_with_peak_limitation|"system efficiency"]] for binary signaling are: | + | *With this condition, there is no [[Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference|"intersymbol interference"]] $\rm (ISI)$ and the maximum eye opening is obtained. |
| + | |||
| + | *Therefore, the [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission#Optimal_binary_receiver_.E2.80.93_.22Matched_Filter.22_realization|"detection SNR"]] and [[Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems#System_optimization_with_peak_limitation|"system efficiency"]] for binary signaling are: | ||
:$$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | :$$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 31: | Line 34: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The optimization task is therefore limited to determining the receiver filter $H_{\rm E}(f)$ such that the normalized noise power before the decision takes the smallest possible value: | + | *The optimization task is therefore limited to determining the receiver filter $H_{\rm E}(f)$ such <br>'''that the normalized noise power before the decision takes the smallest possible value''': |
::<math>\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ::<math>\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ||
| Line 38: | Line 41: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ We refer to the configuration described here as '''Optimal Nyquist Equalization''' | + | $\text{Definition:}$ We refer to the configuration described here as '''Optimal Nyquist Equalization''' $\rm (ONE)$.}} |
| − | == | + | |
| − | + | Although this can also – and especially effectively – be applied to multi-level systems, we initially set $M = 2$. | |
| − | [[File:P ID1424 Dig T 3 5 S2 version2.png|right|frame| | + | |
| − | Let us first clarify the task of the symmetric transversal filter | + | == Operating principle of the transversal filter== |
| + | |||
| + | [[File:P ID1424 Dig T 3 5 S2 version2.png|right|frame|Second order transversal filter as part of the optimal Nyquist equalizer|class=fit]] | ||
| + | <br>Let us first clarify the task of the symmetric transversal filter with frequency response | ||
:$$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ | :$$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ | ||
\hspace{0.4cm} | \hspace{0.4cm} | ||
| Line 49: | Line 55: | ||
$$ | $$ | ||
| − | + | and the following properties: | |
| − | *$N$ indicates the | + | *$N$ indicates the "order" of the filter ⇒ the graph shows a second order filter $(N=2)$. |
| + | |||
*For the filter coefficients $k_{-\lambda} = k_{\lambda}$ ⇒ symmetric structure ⇒ $H_{\rm TF}(f)$ is real. | *For the filter coefficients $k_{-\lambda} = k_{\lambda}$ ⇒ symmetric structure ⇒ $H_{\rm TF}(f)$ is real. | ||
| − | *$H_{\rm TF}(f)$ is thus completely determined by the coefficients $k_0$, ... , $k_N$ | + | |
| + | *$H_{\rm TF}(f)$ is thus completely determined by the coefficients $k_0$, ... , $k_N$. | ||
| − | For the input pulse $g_m(t)$ we assume without restriction of generality that it | + | For the input pulse $g_m(t)$ we assume without restriction of generality that it |
| − | *symmetric about $t=0$ (output of the matched filter),<br> | + | *is symmetric about $t=0$ (output of the matched filter),<br> |
| − | *has the value $g_m(\nu)$ at times $\nu \cdot T$ and $-\nu \cdot T$, respectively.<br> | + | *has the value $g_m(\nu)$ at times $\nu \cdot T$ and $-\nu \cdot T$, respectively.<br> |
| − | Thus, the input pulse values are: | + | Thus, the input pulse values are: |
:$$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | :$$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | ||
{0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | ||
\text{...}\hspace{0.05cm}.$$ | \text{...}\hspace{0.05cm}.$$ | ||
| − | Consequently, for the basic | + | Consequently, for the basic detection pulse $g_d(t)$ at the filter output, the following values result at the time instants $\nu \cdot T$ with the abbreviations $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$: |
:$$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | :$$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | ||
\cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$ | \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$ | ||
| Line 75: | Line 83: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | From this system with three linearly independent equations, one can | + | From this system with three linearly independent equations, one can determine the filter coefficients $k_0$, $k_1$ and $k_2$ in such a way that the basic detection pulse $g_d(t)$ has the following interpolation points: |
:$$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 | :$$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 | ||
,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 | ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 | ||
| Line 87: | Line 95: | ||
\hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$ | \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$ | ||
| − | For the output pulse $g_d(t =0) = 1$ and $g_d(t =\pm T) = 0$ should be valid. For this purpose, a first-order delay filter with coefficients $k_0$ and $k_1$ is suitable, which must satisfy the following conditions: | + | ⇒ For the output pulse $g_d(t =0) = 1$ and $g_d(t =\pm T) = 0$ should be valid. For this purpose, a first-order delay filter with coefficients $k_0$ and $k_1$ is suitable, which must satisfy the following conditions: |
| − | [[File:P ID1425 Dig T 3 5 S2b version1.png|right|frame|Input and output pulse of the optimal Nyquist equalizer]] | + | [[File:P ID1425 Dig T 3 5 S2b version1.png|right|frame|Input and output pulse of the <br>optimal Nyquist equalizer]] |
:$$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | :$$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | ||
\big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow | \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow | ||
| Line 97: | Line 105: | ||
= 1 \hspace{0.05cm}.$$ | = 1 \hspace{0.05cm}.$$ | ||
| − | From this, the optimal filter coefficients $k_0 = 1.116$ and $k_1 = 0.239$ are obtained. | + | From this, the optimal filter coefficients $k_0 = 1.116$ and $k_1 = 0.239$ are obtained. |
| − | *The middle diagram shows that thus the first precursor and the first trailer can be compensated and at the same time $g_d(0) =1$ is valid (yellow background). | + | *The middle diagram shows that thus the first precursor and the first trailer can be compensated and at the same time $g_d(0) =1$ is valid (yellow background). |
| − | *However, the further basic | + | *However, the further basic detection pulse values (blue circles) are different from zero and cause intersymbol interference.<br><br> |
| − | The lower diagram shows that with a second order filter $(N = 2)$ zero crossings are forced at $\pm T$ and at $\pm 2T$ if the coefficients $k_0 = 1.127$, $k_1 = 0.219$ and $k_2 = 0.075$ are suitably chosen. The system of equations for determining the optimal coefficients is thereby: | + | ⇒ The lower diagram shows that with a second order filter $(N = 2)$ zero crossings are forced at $\pm T$ and at $\pm 2T$ if the coefficients $k_0 = 1.127$, $k_1 = 0.219$ and $k_2 = 0.075$ are suitably chosen. The system of equations for determining the optimal coefficients is thereby: |
:$$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 | :$$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 | ||
\cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$ | \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$ | ||
| Line 111: | Line 119: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Conclusion:}$ The results can be generalized as follows: | $\text{Conclusion:}$ The results can be generalized as follows: | ||
| − | + | #With an $N$–th order delay filter, the main value can be made to $g_d(0)=1$ (normalized). | |
| − | + | #The first $N$ trailers $g_{\nu}$ and the first $N$ precursors $g_{-\nu}$ can be made to zero.<br> | |
| − | + | #Further precursors and trailers $(\nu \gt N)$ cannot be compensated in this way. | |
| − | + | #It is even possible that the precursors and trailers outside the compensation range are enlarged or even new ones are created.<br> | |
| − | + | #In the limit $N \to \infty$ (in practice this means: a filter with very many coefficients) a complete Nyquist equalization and thus an ISI-free transmission is possible.}} | |
Revision as of 17:02, 21 June 2022
Contents
- 1 Structure of the optimal Nyquist equalizer
- 2 Operating principle of the transversal filter
- 3 Description in the frequency domain
- 4 Approximation of the optimal Nyquist equalizer
- 5 Calculation of the normalized noise power
- 6 Comparison based on the system efficiency
- 7 Exercises for the chapter
- 8 References
Structure of the optimal Nyquist equalizer
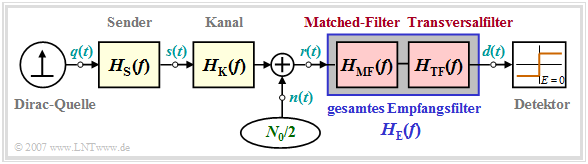
In this section we assume the following block diagram of a binary system. In this regard, it should be noted:
- The "Dirac source" provides the message to be transmitted in binary bipolar form ⇒ amplitude coefficients $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. The source is assumed to be redundancy-free.
- The "transmission pulse shape" $g_s(t)$ is taken into account by the transmitter frequency response $H_{\rm S}(f)$. Mostly, $H_{\rm S}(f) = {\rm sinc}(f T)$ is based ⇒ NRZ rectangular transmission pulses.
- In some derivations, transmitter and channel are combined by the "common frequency response" $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$.
- The receiver filter $H_{\rm E}(f)$ is multiplicatively composed of the matched filter $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ and the transversal filter $H_{\rm TF}(f)$, at least it can be split up mentally in this way.
- The total frequency response between Dirac source and threshold decision should satisfy the "first Nyquist condition". Thus, it must hold:
- $$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) = H_{\rm Nyq}(f) \hspace{0.05cm}.$$
- With this condition, there is no "intersymbol interference" $\rm (ISI)$ and the maximum eye opening is obtained.
- Therefore, the "detection SNR" and "system efficiency" for binary signaling are:
- $$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} = \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} = \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.05cm}.$$
- The optimization task is therefore limited to determining the receiver filter $H_{\rm E}(f)$ such
that the normalized noise power before the decision takes the smallest possible value:
- \[\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \stackrel {!}{=} {\rm minimum}\hspace{0.05cm}.\]
$\text{Definition:}$ We refer to the configuration described here as Optimal Nyquist Equalization $\rm (ONE)$.
Although this can also – and especially effectively – be applied to multi-level systems, we initially set $M = 2$.
Operating principle of the transversal filter
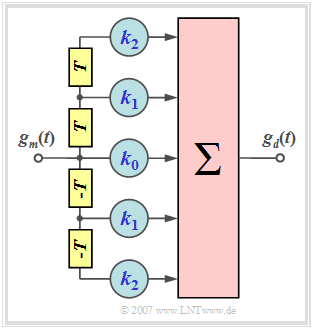
Let us first clarify the task of the symmetric transversal filter with frequency response
- $$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) $$
and the following properties:
- $N$ indicates the "order" of the filter ⇒ the graph shows a second order filter $(N=2)$.
- For the filter coefficients $k_{-\lambda} = k_{\lambda}$ ⇒ symmetric structure ⇒ $H_{\rm TF}(f)$ is real.
- $H_{\rm TF}(f)$ is thus completely determined by the coefficients $k_0$, ... , $k_N$.
For the input pulse $g_m(t)$ we assume without restriction of generality that it
- is symmetric about $t=0$ (output of the matched filter),
- has the value $g_m(\nu)$ at times $\nu \cdot T$ and $-\nu \cdot T$, respectively.
Thus, the input pulse values are:
- $$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} \text{...}\hspace{0.05cm}.$$
Consequently, for the basic detection pulse $g_d(t)$ at the filter output, the following values result at the time instants $\nu \cdot T$ with the abbreviations $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$:
- $$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$
- $$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 \cdot \big [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3) \big ], $$
- $$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 \cdot \big [g_m(1)+g_m(3)\big ]+ k_2 \cdot \big [g_m(2)+g_m(4)\big ] \hspace{0.05cm}. $$
From this system with three linearly independent equations, one can determine the filter coefficients $k_0$, $k_1$ and $k_2$ in such a way that the basic detection pulse $g_d(t)$ has the following interpolation points:
- $$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} \text{...}$$
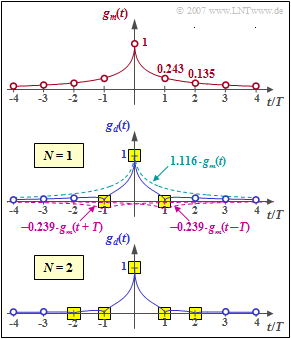
$\text{Example 1:}$ We assume the symmetrical input signal according to the upper diagram in the graph. With the abbreviation $g_m(\nu)= g_m(\pm \nu \cdot T)$ there are the following samples at the distance of the symbol duration $T$:
- $$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= 0.243,\hspace{0.35cm}g_m(2)= 0.135,\hspace{0.35cm}g_m(3)= 0.086, \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$
⇒ For the output pulse $g_d(t =0) = 1$ and $g_d(t =\pm T) = 0$ should be valid. For this purpose, a first-order delay filter with coefficients $k_0$ and $k_1$ is suitable, which must satisfy the following conditions:
- $$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{k_1} = -0.214 \cdot {k_0}\hspace{0.05cm},$$
- $$ t = 0 \hspace{-0.1cm} : \hspace{0.6cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243= 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm}0.896 \cdot {k_0} = 1 \hspace{0.05cm}.$$
From this, the optimal filter coefficients $k_0 = 1.116$ and $k_1 = 0.239$ are obtained.
- The middle diagram shows that thus the first precursor and the first trailer can be compensated and at the same time $g_d(0) =1$ is valid (yellow background).
- However, the further basic detection pulse values (blue circles) are different from zero and cause intersymbol interference.
⇒ The lower diagram shows that with a second order filter $(N = 2)$ zero crossings are forced at $\pm T$ and at $\pm 2T$ if the coefficients $k_0 = 1.127$, $k_1 = 0.219$ and $k_2 = 0.075$ are suitably chosen. The system of equations for determining the optimal coefficients is thereby:
- $$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$
- $$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000+0.135 \big ]+ k_2 \cdot \big [0.243+0.086 \big ] = 0\hspace{0.05cm},$$
- $$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot \big [0.243+0.086\big ]+ k_2 \cdot \big [1.000 + 0.059 \big ]= 0 \hspace{0.05cm}.$$
$\text{Conclusion:}$ The results can be generalized as follows:
- With an $N$–th order delay filter, the main value can be made to $g_d(0)=1$ (normalized).
- The first $N$ trailers $g_{\nu}$ and the first $N$ precursors $g_{-\nu}$ can be made to zero.
- Further precursors and trailers $(\nu \gt N)$ cannot be compensated in this way.
- It is even possible that the precursors and trailers outside the compensation range are enlarged or even new ones are created.
- In the limit $N \to \infty$ (in practice this means: a filter with very many coefficients) a complete Nyquist equalization and thus an ISI-free transmission is possible.
Description in the frequency domain
The fact that the optimal Nyquist equalizer is multiplicatively derived from
- the matched filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – i.e. matched to the basic receiver pulse $g_r(t)$ – and
- a transversal filter $H_{\rm MF}(f)$ with infinitely many filter coefficients
follows from the first Nyquist criterion. By applying the "calculus of variations", the frequency response of the transversal filter is obtained – see [TS87][1]:
- $$H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - \frac{\kappa}{T}) |^2} \hspace{0.3cm}{\rm{mit}}\hspace{0.3cm}H_{\rm SK}(f) = H_{\rm S}(f)\cdot H_{\rm K}(f) \hspace{0.05cm}.$$
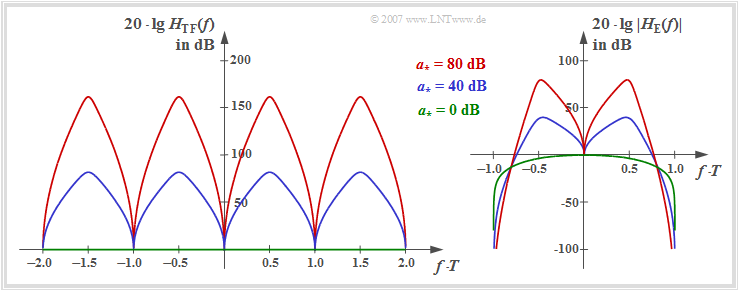
The left graph shows the function $20 \cdot \lg \ H_{\rm TF}(f)$ in the range $| f | \le 1/T$. This assumes rectangular NRZ transmission pulses and a coaxial cable with the characteristic cable attenuation $a_\star$.
One can see from the above equation and the left graph:
- $H_{\rm TF}(f)$ is real, which results in the symmetrical structure of the transversal filter: $k_{-\lambda} =k_{+\lambda} $.
- $H_{\rm TF}(f)$ is at the same time a function periodic with frequency $1/T$.
- The coefficients are thus obtained from the "Fourier series" (applied to the spectral function):
- $$k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2} \hspace{0.2cm} {\rm d} f \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = \sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.$$
The right graph shows the frequency response $20 \cdot \lg \ |H_{\rm E}(f)|$ of the entire receiver filter including the matched filter. It holds:
- $$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}.$$
To these representations it is to be noted:
- For $a_\star = 0 \ \rm dB$ (ideal channel, green zero line) the transversal filter $H_{\rm TF}(f)$ can be omitted and it is valid for NRZ rectangular pulses as already derived in the section "Optimal binary receiver – "Matched Filter" realization":
- $$H_{\rm E}(f) =H_{\rm S}(f) = {\rm sinc} (f T).$$
- While the transversal filter frequency response $H_{\rm TF}(f)$ is symmetrical to the Nyquist frequency $f_{\rm Nyq} = 1/(2T)$ at $a_\star \ne 0 \ \rm dB$, this symmetry is no longer given for the receiver filter overall frequency response $H_{\rm E}(f)$.
- The maxima of the frequency responses $H_{\rm TF}(f)$ and $|H_{\rm E}(f)|$ depend significantly on the characteristic cable attenuation $a_\star$. From the blue and red function curves, respectively, can be read:
- $$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)| \ \big] \approx 40\,{\rm dB}\hspace{0.05cm},$$
- $$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big] \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)|\ \big] \approx 80\,{\rm dB}\hspace{0.05cm}.$$
Approximation of the optimal Nyquist equalizer
We now consider the overall frequency response between the Dirac source and the decision.
- This is made up multiplicatively of the frequency responses of the transmitter, channel and receiver.
- According to the derivation, the total frequency response must satisfy the Nyquist condition:
- $$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = \frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}\hspace{0.05cm}.$$
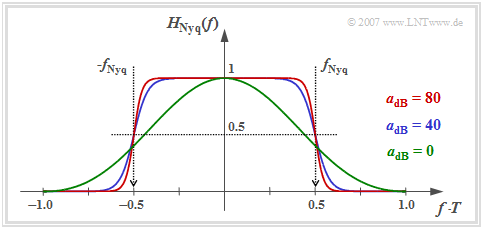
The graph shows the following properties of the optimal Nyquist equalizer (ONE):
- If the cable attenuation is sufficiently large $(a_\star \ge 10 \ \rm dB)$, the overall frequency response can be described with good approximation by the "cosine rolloff low-pass filter".
- The larger $a_\star$ is, the smaller is the rolloff factor $r$ and the steeper is the edge drop. For the characteristic cable attenuation $a_\star = 40 \ \rm dB$ (blue curve) we get $r \approx 0.4$, for $a_\star = 80 \ \rm dB$ (red curve) $r \approx 0.18$.
- Above the frequency $f_{\rm Nyq} \cdot (1 + r)$, $H_{\rm Nyq}(f)$ has no components. However, with ideal channel ⇒ $a_\star = 0 \ \rm dB$ (green curve), $H_{\rm Nyq}(f)= {\rm sinc}^2(f T)$ theoretically extends to infinity.
The interactive applet "Frequency & Impulse Responses" illustrates, among other things, the properties of the cosine rolloff low–pass filter.
Calculation of the normalized noise power
We now consider the (normalized) noise power at the decision. For this holds:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ (2T)} =T \cdot \int_{-1/(2T)}^{+1/(2T)} |H_{\rm E}(f)|^2 \,{\rm d} f .$$
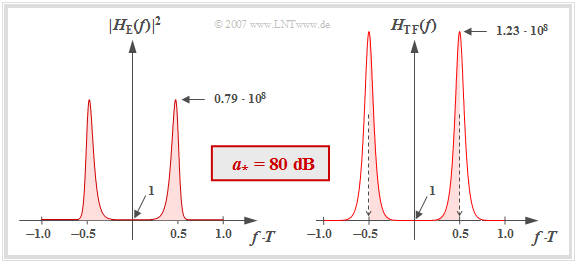
- The left plot of the graph shows $|H_{\rm E}(f)|^2$ in linear scale for the characteristic cable attenuation $a_\star = 80 \ \rm dB$. Note that $|H_{\rm E}(f = 0)|^2 = 1$.
- Since the frequency has been normalized to $1/T$ in this plot, the normalized noise power corresponds exactly to the area (highlighted in red) under this curve. The numerical evaluation results in:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = 1.68 \cdot 10^7\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 \approx 72.25\,{\rm dB} \hspace{0.05cm}.$$
- It can be shown that the normalized noise power can be calculated using the transverse filter frequency response $H_{\rm TF}(f)$ alone, as shown in the right graph:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f \hspace{0.3cm}(= k_0)\hspace{0.05cm}.$$
- The red surfaces are exactly the same in both images.
$\text{Conclusion:}$ The normalized noise power of the optimal Nyquist equalizer is equal to the Fourier coefficient $k_0$ when the real, symmetric, and periodic transverse filter frequency response $H_{\rm TF}(f)$ is represented as a Fourier series.
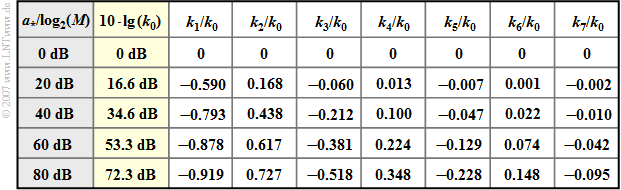
- In the second column of the table, $10 \cdot \lg \ (k_0)$ is given depending on the characteristic cable attenuation $a_\star$ of a coaxial cable.
- Due to the chosen normalization, the table is also valid for "redundancy-free multi-level systems"; here $M$ denotes the level number.
- The coefficients $k_1$, $k_2$, $k_3$, ... of the transversal filter have alternating signs for $a_\star \ne 0 \ \rm dB$.
- For $a_\star = 40 \ \rm dB$, four coefficients are greater in magnitude than $k_0/10$, and for $a_\star = 80 \ \rm dB$ even seven.
Comparison based on the system efficiency
For a system comparison, the "system efficiency" is suitable, which relates the achievable detection SNR $\rho_d$ to the maximum SNR $\rho_{d, \ {\rm max}}$, which, however, is only achievable for ideal channel $H_{\rm K}(f) \equiv 1$. For the system efficiency, with $M$–level transmission and optimal Nyquist equalization:
- $$\eta = \frac{\rho_d}{s_0^2 \cdot T / N_0}=\frac{{\rm log_2}\hspace{0.1cm}M}{(M-1)^2 \cdot k_0}.$$
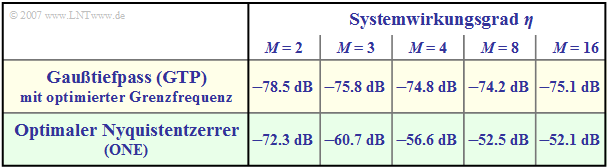
The (normalized) noise power $k_0$ can be read from the "table" in the last sec tion. Note the normalization of the characteristic cable attenuation $a_\star$ in the first column. The following table from [TS87][1] allows a system comparison for the characteristic cable attenuation $a_\star = 80 \ \rm dB$.
Compared are:
- the "Gaussian total frequency response" $\text{(GTP)}$, which leads to an intersymbol interference system even when optimized,
- the "optimal Nyquist equalizer" $\text{(ONE)}$, with which intersymbol interference is excluded per se.
$\text{Conclusion:}$ The results of this system comparison can be summarized as follows:
- In the binary case $(M = 2)$, the intersymbol interference-free system $\text{(ONE)}$ outperforms the intersymbol interference system $\text{(GTP)}$ by about $6 \ \rm dB$.
- If the optimal Nyquist equalization is applied to multilevel systems, a further, significant gain in signal-to-noise ratio is possible compared to $\text{GTP}$. For $M =4$, this gain is about $18.2 \ \rm dB$.
- However, the narrowband $\text{GTP}$ system can be significantly improved by using a receiver with decision feedback. This will be discussed in the next chapter.
At this point we refer to the interactive applet "Linear Nyquist Equalization".
Exercises for the chapter
Exercise 3.6: Transversal Filter of the Optimal Nyquist Equalizer
Exercise 3.6Z: Optimum Nyquist Equalizer for Exponential Pulse
Exercise 3.7: Optimal Nyquist Equalization once again
Exercise 3.7Z: Regenerator Field Length
References