Difference between revisions of "Digital Signal Transmission/Linear Nyquist Equalization"
| (41 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Intersymbol Interfering and Equalization Methods |
|Vorherige Seite=Impulsinterferenzen bei mehrstufiger Übertragung | |Vorherige Seite=Impulsinterferenzen bei mehrstufiger Übertragung | ||
|Nächste Seite=Entscheidungsrückkopplung | |Nächste Seite=Entscheidungsrückkopplung | ||
}} | }} | ||
| − | == | + | == Structure of the optimal Nyquist equalizer == |
<br> | <br> | ||
| − | In | + | In this section we assume the following block diagram of a binary system. In this regard, it should be noted: |
| + | [[File:EN_Dig_T_3_5_S1.png|right|frame|Block diagram of the optimal Nyquist equalizer|class=fit]] | ||
| − | + | *The "Dirac source" provides the message to be transmitted in binary bipolar form ⇒ amplitude coefficients $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. The source is assumed to be redundancy-free. | |
| − | + | *The "transmission pulse shape" $g_s(t)$ is taken into account by the transmitter frequency response $H_{\rm S}(f)$. Mostly, $H_{\rm S}(f) = {\rm sinc}(f T)$ is based ⇒ NRZ rectangular transmission pulses. | |
| − | * | ||
| − | * | + | *In some derivations, transmitter and channel are combined by the "common frequency response" $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$. <br> |
| − | * | + | *The receiver filter $H_{\rm E}(f)$ is multiplicatively composed of the [[Theory_of_Stochastic_Signals/Matched_Filter|matched filter]] $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ and the [[Digital_Signal_Transmission/Linear_Nyquist_Equalization#Operating_principle_of_the_transversal_filter|transversal filter]] $H_{\rm TF}(f)$, at least it can be split up mentally in this way. |
| − | * | + | *The overall frequency response between Dirac source and threshold decision should satisfy the [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_frequency_domain| "first Nyquist condition"]]. Thus, it must hold: |
| − | |||
| − | |||
:$$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) | :$$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) | ||
= H_{\rm Nyq}(f) | = H_{\rm Nyq}(f) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *With this condition, there is no [[Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference|"intersymbol interference"]] $\rm (ISI)$ and the maximum eye opening is obtained. |
| + | |||
| + | *Therefore, the [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission#Optimal_binary_receiver_.E2.80.93_.22Matched_Filter.22_realization|"detection SNR"]] and [[Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems#System_optimization_with_peak_limitation|"system efficiency"]] for binary signaling are: | ||
:$$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | :$$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 34: | Line 34: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The optimization task is therefore limited to determining the receiver filter $H_{\rm E}(f)$ such <br>'''that the normalized noise power before the decision takes the smallest possible value''': |
::<math>\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ::<math>\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ||
T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 | T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 | ||
| − | \,{\rm d} f \stackrel {!}{=} {\rm | + | \,{\rm d} f \stackrel {!}{=} {\rm minimum}\hspace{0.05cm}.</math> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ We refer to the configuration described here as '''Optimal Nyquist Equalization''' $\rm (ONE)$.}} |
| + | |||
| − | == | + | Although this can also – and especially effectively – be applied to multi-level systems, we initially set $M = 2$. |
| − | + | ||
| − | [[File:P ID1424 Dig T 3 5 S2 version2.png|right|frame| | + | == Operating principle of the transversal filter== |
| − | + | ||
| + | [[File:P ID1424 Dig T 3 5 S2 version2.png|right|frame|Second order transversal filter as part of the optimal Nyquist equalizer|class=fit]] | ||
| + | <br>Let us first clarify the task of the symmetric transversal filter with frequency response | ||
:$$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ | :$$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ | ||
\hspace{0.4cm} | \hspace{0.4cm} | ||
| Line 52: | Line 55: | ||
$$ | $$ | ||
| − | + | and the following properties: | |
| − | *$N$ | + | *$N$ indicates the "order" of the filter ⇒ the graph shows a second order filter $(N=2)$. |
| − | * | + | |
| − | *$H_{\rm TF}(f)$ | + | *For the filter coefficients $k_{-\lambda} = k_{\lambda}$ ⇒ symmetric structure ⇒ $H_{\rm TF}(f)$ is real. |
| + | |||
| + | *$H_{\rm TF}(f)$ is thus completely determined by the coefficients $k_0$, ... , $k_N$. | ||
| − | + | For the input pulse $g_m(t)$ we assume without restriction of generality that it | |
| − | * | + | *is symmetric about $t=0$ (output of the matched filter),<br> |
| − | * | + | *has the value $g_m(\nu)$ at times $\nu \cdot T$ and $-\nu \cdot T$, respectively.<br> |
| − | + | Thus, the input pulse values are: | |
:$$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | :$$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | ||
{0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | ||
\text{...}\hspace{0.05cm}.$$ | \text{...}\hspace{0.05cm}.$$ | ||
| − | + | Consequently, for the basic detection pulse $g_d(t)$ at the filter output, the following values result at the time instants $\nu \cdot T$ with the abbreviations $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$: | |
:$$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | :$$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | ||
\cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$ | \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$ | ||
:$$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 | :$$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 | ||
| − | \cdot [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3)], $$ | + | \cdot \big [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3) \big ], $$ |
:$$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 | :$$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 | ||
| − | \cdot [g_m(1)+g_m(3)]+ k_2 \cdot [g_m(2)+g_m(4)] | + | \cdot \big [g_m(1)+g_m(3)\big ]+ k_2 \cdot \big [g_m(2)+g_m(4)\big ] |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | From this system with three linearly independent equations, one can determine the filter coefficients $k_0$, $k_1$ and $k_2$ in such a way that the basic detection pulse $g_d(t)$ has the following interpolation points: | |
:$$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 | :$$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 | ||
,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 | ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 | ||
| Line 84: | Line 89: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We assume the symmetrical input signal according to the upper diagram in the graph. With the abbreviation $g_m(\nu)= g_m(\pm \nu \cdot T)$ there are the following samples at the distance of the symbol duration $T$: |
:$$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} | :$$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= | \Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= | ||
| Line 90: | Line 95: | ||
\hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$ | \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$ | ||
| − | + | ⇒ For the output pulse $g_d(t =0) = 1$ and $g_d(t =\pm T) = 0$ should be valid. For this purpose, a first-order delay filter with coefficients $k_0$ and $k_1$ is suitable, which must satisfy the following conditions: | |
| − | [[File:P ID1425 Dig T 3 5 S2b version1.png|right|frame| | + | [[File:P ID1425 Dig T 3 5 S2b version1.png|right|frame|Input and output pulse of the <br>optimal Nyquist equalizer]] |
:$$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | :$$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | ||
| − | [1.000 +0.135] = 0\hspace{0.3cm}\Rightarrow | + | \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow |
\hspace{0.3cm}{k_1} = | \hspace{0.3cm}{k_1} = | ||
-0.214 \cdot {k_0}\hspace{0.05cm},$$ | -0.214 \cdot {k_0}\hspace{0.05cm},$$ | ||
| Line 100: | Line 105: | ||
= 1 \hspace{0.05cm}.$$ | = 1 \hspace{0.05cm}.$$ | ||
| − | + | From this, the optimal filter coefficients $k_0 = 1.116$ and $k_1 = 0.239$ are obtained. | |
| − | * | + | *The middle diagram shows that thus the first precursor and the first trailer can be compensated and at the same time $g_d(0) =1$ is valid (yellow background). |
| − | |||
| + | *However, the further basic detection pulse values (blue circles) are different from zero and cause intersymbol interference.<br><br> | ||
| − | + | ⇒ The lower diagram shows that with a second order filter $(N = 2)$ zero crossings are forced at $\pm T$ and at $\pm 2T$ if the coefficients $k_0 = 1.127$, $k_1 = 0.219$ and $k_2 = 0.075$ are suitably chosen. The system of equations for determining the optimal coefficients is thereby: | |
:$$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 | :$$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 | ||
\cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$ | \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$ | ||
:$$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | :$$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | ||
| − | [1.000+0.135]+ k_2 \cdot [0.243+0.086] = 0\hspace{0.05cm},$$ | + | \big [1.000+0.135 \big ]+ k_2 \cdot \big [0.243+0.086 \big ] = 0\hspace{0.05cm},$$ |
:$$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot | :$$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot | ||
| − | [0.243+0.086]+ k_2 \cdot [1.000 + 0.059]= 0 \hspace{0.05cm}.$$}}<br> | + | \big [0.243+0.086\big ]+ k_2 \cdot \big [1.000 + 0.059 \big ]= 0 \hspace{0.05cm}.$$}}<br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ The results can be generalized as follows: |
| − | + | #With an $N$–th order delay filter, the main value can be made to $g_d(0)=1$ (normalized). | |
| − | + | #The first $N$ trailers $g_{\nu}$ and the first $N$ precursors $g_{-\nu}$ can be made to zero.<br> | |
| − | + | #Further precursors and trailers $(\nu \gt N)$ cannot be compensated in this way. | |
| − | + | #It is even possible that the precursors and trailers outside the compensation range are enlarged or even new ones are created.<br> | |
| − | + | #In the limit $N \to \infty$ (in practice this means: a filter with very many coefficients) a complete Nyquist equalization and thus an ISI-free transmission is possible.}} | |
| − | == | + | == Description in the frequency domain == |
<br> | <br> | ||
| − | + | The fact that the optimal Nyquist equalizer is multiplicatively derived from | |
| − | * | + | *the matched filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – i.e. matched to the basic receiver pulse $g_r(t)$ – and<br> |
| − | * | + | *a transversal filter $H_{\rm MF}(f)$ with infinitely many filter coefficients<br><br> |
| − | + | follows from the first Nyquist criterion. By applying the [https://en.wikipedia.org/wiki/Calculus_of_variations "Calculus of Variations"], the frequency response of the transversal filter is obtained – see [TS87]<ref name='TS87'>Tröndle, K.; Söder, G.: Optimization of Digital Transmission Systems. Boston – London: Artech House, 1987, ISBN: 0-89006-225-0.</ref>: | |
| − | :$$H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | + | [[File:Dig_T_3_5_S3b_version2.png|right|frame|Magnitude frequency response of the transversal filter (left) and the entire optimal Nyquist equalizer (right)|class=fit]] |
| + | $$H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
\frac{\kappa}{T}) | \frac{\kappa}{T}) | ||
| − | |^2} \ | + | |^2},$$ |
| − | \ | + | $$\text{where }H_{\rm SK}(f) = H_{\rm S}(f)\cdot H_{\rm K}(f).$$ |
| + | |||
| + | The left graph shows $20 \cdot \lg \ H_{\rm TF}(f)$ in the range $| f | \le 1/T$. This assumes rectangular NRZ transmission pulses and a coaxial cable with the characteristic cable attenuation $a_\star$. | ||
| − | + | One can see from the equation and the left graph: | |
| + | *$H_{\rm TF}(f)$ is "real", which results in the symmetrical structure of the transversal filter: $k_{-\lambda} =k_{+\lambda} $.<br> | ||
| − | + | *$H_{\rm TF}(f)$ is at the same time "periodic" with frequency $1/T$. | |
| − | + | *The coefficients are thus obtained from the [[Signal_Representation/Fourier_Series|"Fourier series"]] (applied to the spectral function): | |
| − | * | ||
| − | |||
| − | |||
:$$k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | :$$k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
{\kappa}/{T}) | {\kappa}/{T}) | ||
| − | |^2} \hspace{0.2cm} {\rm d} f \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = | + | |^2} \hspace{0.2cm} {\rm d} f$$ |
| + | :$$ \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = | ||
\sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm | \sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm | ||
e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.$$ | e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.$$ | ||
| + | The right graph shows the frequency response $20 \cdot \lg \ |H_{\rm E}(f)|$ of the entire receiver filter including the matched filter. It holds: | ||
| − | + | :$$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | |
| − | |||
| − | :$$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{ | ||
{\kappa}/{T}) | {\kappa}/{T}) | ||
|^2}.$$ | |^2}.$$ | ||
| − | + | To these representations it is to be noted: | |
| − | * | + | *For $a_\star = 0 \ \rm dB$ (ideal channel, green zero line) the transversal filter $H_{\rm TF}(f)$ can be omitted and it is valid for NRZ rectangular pulses as already derived in the section [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission#Optimal_binary_receiver_.E2.80.93_.22Matched_Filter.22_realization|"Optimal binary receiver – "Matched Filter" realization"]]: |
| − | * | + | :$$H_{\rm E}(f) =H_{\rm S}(f) = {\rm sinc} (f T).$$ |
| − | * | + | *While the transversal filter frequency response $H_{\rm TF}(f)$ is symmetrical to the Nyquist frequency $f_{\rm Nyq} = 1/(2T)$ at $a_\star \ne 0 \ \rm dB$, this symmetry is no longer given for the receiver filter overall frequency response $H_{\rm E}(f)$. <br> |
| − | :$$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}[H_{\rm | + | |
| − | TF}(f)]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm | + | *The maxima of the frequency responses $H_{\rm TF}(f)$ and $|H_{\rm E}(f)|$ depend significantly on the characteristic cable attenuation $a_\star$. From the blue and red function curves, respectively, can be read: |
| − | Max}[\ |H_{\rm E}(f)| \ ] \approx 40\,{\rm dB}\hspace{0.05cm},$$ | + | :$$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm |
| − | :$$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}[H_{\rm TF}(f)] | + | TF}(f)\big]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm |
| − | \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}[\ |H_{\rm E}(f)|\ ] | + | Max}\big[\ |H_{\rm E}(f)| \ \big] \approx 40\,{\rm dB}\hspace{0.05cm},$$ |
| + | :$$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big] | ||
| + | \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)|\ \big] | ||
\approx 80\,{\rm dB}\hspace{0.05cm}.$$ | \approx 80\,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | == Approximation | + | == Approximation of the optimal Nyquist equalizer == |
<br> | <br> | ||
| − | + | We now consider the overall frequency response between the Dirac source and the decision. | |
| + | *This is made up multiplicatively of the frequency responses of the transmitter, channel and receiver. | ||
| + | *According to the derivation, the overall frequency response must satisfy the Nyquist condition: | ||
| + | [[File:P ID1428 Dig T 3 5 S3c version1.png|right|frame|Optimum overall Nyquist frequency response for a coaxial cable system|class=fit]] | ||
| + | |||
:$$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = | :$$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = | ||
\frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | \frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
| Line 176: | Line 188: | ||
|^2}\hspace{0.05cm}.$$ | |^2}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | + | The graph shows the following properties of the '''optimal Nyquist equalizer''' $\rm (ONE)$: | |
| + | *If the cable attenuation is sufficiently large $(a_\star \ge 10 \ \rm dB)$, the overall frequency response can be described with good approximation by the [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#1.2FT_Nyquist_spectra| "cosine rolloff low-pass"]]. <br> | ||
| − | * | + | *The larger $a_\star$ is, the smaller is the rolloff factor $r$ and the steeper is the edge drop. For the characteristic cable attenuation $a_\star = 40 \ \rm dB$ (blue curve) we get $r \approx 0.4$, for $a_\star = 80 \ \rm dB$ (red curve) $r \approx 0.18$.<br> |
| − | + | *Above the frequency $f_{\rm Nyq} \cdot (1 + r)$, $H_{\rm Nyq}(f)$ has no components. However, with ideal channel ⇒ $a_\star = 0 \ \rm dB$ (green curve), $H_{\rm Nyq}(f)= {\rm sinc}^2(f T)$ theoretically extends to infinity. | |
| − | |||
| − | |||
| − | |||
| − | == | + | |
| + | The interactive applet [[Applets:Frequency_%26_Impulse_Responses|"Frequency & Impulse Responses"]] illustrates, among other things, the properties of the "cosine rolloff low–pass". | ||
| + | |||
| + | |||
| + | == Calculation of the normalized noise power == | ||
<br> | <br> | ||
| − | + | We now consider the (normalized) noise power at the decision. For this holds: | |
:$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ | ||
| Line 196: | Line 208: | ||
\,{\rm d} f .$$ | \,{\rm d} f .$$ | ||
| − | + | [[File:P ID1429 Dig T 3 5 S5 version1.png|right|frame|To calculate the normalized noise power at the optimal Nyquist equalizer $\rm (ONE)$|class=fit]] | |
| + | *The left plot shows $|H_{\rm E}(f)|^2$ in linear scale for the characteristic cable attenuation $a_\star = 80 \ \rm dB$. Note that $|H_{\rm E}(f = 0)|^2 = 1$. | ||
| − | + | *Since the frequency has been normalized to $1/T$ in this plot, the normalized noise power corresponds exactly to the area (highlighted in red) under this curve. The numerical evaluation results in: | |
| − | + | ||
| − | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = 1.68 \cdot 10^7 | + | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = 1.68 \cdot 10^7\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm |
| − | |||
lg}\hspace{0.1cm}\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 \approx | lg}\hspace{0.1cm}\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 \approx | ||
72.25\,{\rm dB} \hspace{0.05cm}.$$ | 72.25\,{\rm dB} \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | + | *It can be shown that the normalized noise power can be calculated using the transversal filter frequency response $H_{\rm TF}(f)$ alone, as shown in the right graph: | |
:$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot | ||
\int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f | \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f | ||
\hspace{0.3cm}(= k_0)\hspace{0.05cm}.$$ | \hspace{0.3cm}(= k_0)\hspace{0.05cm}.$$ | ||
| − | + | *The red areas are exactly the same in both images. | |
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Conclusion:}$ The normalized noise power of the optimal Nyquist equalizer is equal to the Fourier coefficient $k_0$ when the real, symmetric, and periodic transversal filter frequency response $H_{\rm TF}(f)$ is represented as a Fourier series. | ||
| − | + | [[File:P ID1430 Dig T 3 5 S5b version3.png|right|frame|Coefficients of the optimal Nyquist equalizer $\rm (ONE)$|class=fit]] | |
| − | + | *In the second column of the table, $10 \cdot \lg \ (k_0)$ is given depending on the characteristic cable attenuation $a_\star$ of a coaxial cable. | |
| − | *In | + | |
| − | * | + | *Due to the chosen normalization, the table is also valid for [[Digital_Signal_Transmission/Intersymbol_Interference_for_Multi-Level_Transmission#Eye_opening_for_redundancy-free_multi-level_systems|"redundancy-free multi-level systems"]]; here $M$ denotes the level number.<br> |
| − | |||
| − | |||
| − | + | *The coefficients $k_1$, $k_2$, $k_3$, ... of the transversal filter have alternating signs for $a_\star \ne 0 \ \rm dB$. | |
| + | |||
| + | *For $a_\star = 40 \ \rm dB$, four coefficients are greater in magnitude than $k_0/10$, and for $a_\star = 80 \ \rm dB$ even seven.}} | ||
| − | == | + | == Comparison based on the system efficiency == |
<br> | <br> | ||
| − | + | For a system comparison, the [[Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems#System_optimization_with_power_limitation|"system efficiency"]] is suitable, which relates the achievable detection SNR $\rho_d$ to the maximum SNR $\rho_{d, \ {\rm max}}$, which, however, is only achievable for ideal channel $H_{\rm K}(f) \equiv 1$. | |
| + | |||
| + | [[File:EN_Dig_T_3_5_S6_neu.png|right|frame|Comparison of binary and multi-level transmission systems according to $\text{GLP}$ and $\text{ONE}$|class=fit]] | ||
| + | For the system efficiency, with $M$–level transmission and optimal Nyquist equalization: | ||
:$$\eta = \frac{\rho_d}{s_0^2 \cdot T / N_0}=\frac{{\rm log_2}\hspace{0.1cm}M}{(M-1)^2 \cdot k_0}.$$ | :$$\eta = \frac{\rho_d}{s_0^2 \cdot T / N_0}=\frac{{\rm log_2}\hspace{0.1cm}M}{(M-1)^2 \cdot k_0}.$$ | ||
| − | + | *The (normalized) noise power $k_0$ can be read from the [[Digital_Signal_Transmission/Linear_Nyquist_Equalization#Calculation_of_the_normalized_noise_power|'''table''']] in the last section. | |
| + | |||
| + | *Note the normalization of the characteristic cable attenuation $a_\star$ in the first column. | ||
| − | + | *The table on the right from [TS87]<ref name='TS87'/> allows a system comparison for the characteristic cable attenuation $a_\star = 80 \ \rm dB$. | |
| − | |||
| − | |||
| − | + | Compared are: | |
| + | * the [[Digital_Signal_Transmission/Berücksichtigung_von_Kanalverzerrungen_und_Entzerrung|"Gaussian overall frequency response"]] $\text{(GLP)}$, which leads to an intersymbol interference system even when optimized, <br> | ||
| − | * | + | *the [[Digital_Signal_Transmission/Linear_Nyquist_Equalization#Structure_of_the_optimal_Nyquist_equalizer|"optimal Nyquist equalizer"]] $\text{(ONE)}$; here, intersymbol interference is excluded per se. |
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ The results of this system comparison can be summarized as follows: |
| − | + | #In the binary case $(M = 2)$, the intersymbol interference-free system $\text{(ONE)}$ outperforms the intersymbol interference system $\text{(GLP)}$ by about $6 \ \rm dB$. <br> | |
| − | + | #If the optimal Nyquist equalization is applied to multi-level systems, a further, significant gain in signal-to-noise ratio is possible compared to $\text{GLP}$. | |
| − | + | #For $M =4$, this gain is about $18.2 \ \rm dB$.<br> | |
| + | #However, the narrowband $\text{GLP}$ system can be significantly improved by using a receiver with decision feedback. This will be discussed in the next chapter.}}<br> | ||
| + | |||
| + | ⇒ At this point we refer to the (German language) SWF applet [[Applets:Lineare_Nyquistentzerrung|"Lineare Nyquistentzerrung"]] ⇒ "Linear Nyquist Equalization". | ||
| + | |||
| − | |||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.6:_Transversal_Filter_of_the_Optimal_Nyquist_Equalizer| Exercise 3.6: Transversal Filter of the Optimal Nyquist Equalizer]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.6Z:Optimum_Nyquist_Equalizer_for_Exponential_Pulse| Exercise 3.6Z: Optimum Nyquist Equalizer for Exponential Pulse]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.7:_Optimal_Nyquist_Equalization_once_again|Exercise 3.7: Optimal Nyquist Equalization once again]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.7Z:_Regenerator_Field_Length|Exercise 3.7Z: Regenerator Field Length]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
Latest revision as of 11:21, 13 July 2022
Contents
- 1 Structure of the optimal Nyquist equalizer
- 2 Operating principle of the transversal filter
- 3 Description in the frequency domain
- 4 Approximation of the optimal Nyquist equalizer
- 5 Calculation of the normalized noise power
- 6 Comparison based on the system efficiency
- 7 Exercises for the chapter
- 8 References
Structure of the optimal Nyquist equalizer
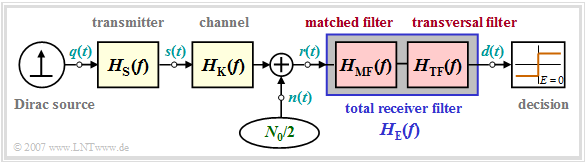
In this section we assume the following block diagram of a binary system. In this regard, it should be noted:
- The "Dirac source" provides the message to be transmitted in binary bipolar form ⇒ amplitude coefficients $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. The source is assumed to be redundancy-free.
- The "transmission pulse shape" $g_s(t)$ is taken into account by the transmitter frequency response $H_{\rm S}(f)$. Mostly, $H_{\rm S}(f) = {\rm sinc}(f T)$ is based ⇒ NRZ rectangular transmission pulses.
- In some derivations, transmitter and channel are combined by the "common frequency response" $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$.
- The receiver filter $H_{\rm E}(f)$ is multiplicatively composed of the matched filter $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ and the transversal filter $H_{\rm TF}(f)$, at least it can be split up mentally in this way.
- The overall frequency response between Dirac source and threshold decision should satisfy the "first Nyquist condition". Thus, it must hold:
- $$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) = H_{\rm Nyq}(f) \hspace{0.05cm}.$$
- With this condition, there is no "intersymbol interference" $\rm (ISI)$ and the maximum eye opening is obtained.
- Therefore, the "detection SNR" and "system efficiency" for binary signaling are:
- $$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} = \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} = \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.05cm}.$$
- The optimization task is therefore limited to determining the receiver filter $H_{\rm E}(f)$ such
that the normalized noise power before the decision takes the smallest possible value:
- \[\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \stackrel {!}{=} {\rm minimum}\hspace{0.05cm}.\]
$\text{Definition:}$ We refer to the configuration described here as Optimal Nyquist Equalization $\rm (ONE)$.
Although this can also – and especially effectively – be applied to multi-level systems, we initially set $M = 2$.
Operating principle of the transversal filter
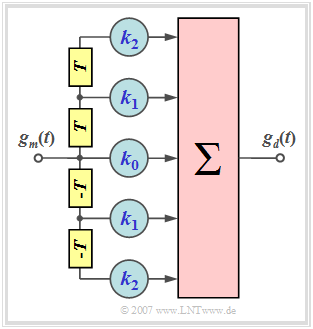
Let us first clarify the task of the symmetric transversal filter with frequency response
- $$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) $$
and the following properties:
- $N$ indicates the "order" of the filter ⇒ the graph shows a second order filter $(N=2)$.
- For the filter coefficients $k_{-\lambda} = k_{\lambda}$ ⇒ symmetric structure ⇒ $H_{\rm TF}(f)$ is real.
- $H_{\rm TF}(f)$ is thus completely determined by the coefficients $k_0$, ... , $k_N$.
For the input pulse $g_m(t)$ we assume without restriction of generality that it
- is symmetric about $t=0$ (output of the matched filter),
- has the value $g_m(\nu)$ at times $\nu \cdot T$ and $-\nu \cdot T$, respectively.
Thus, the input pulse values are:
- $$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} \text{...}\hspace{0.05cm}.$$
Consequently, for the basic detection pulse $g_d(t)$ at the filter output, the following values result at the time instants $\nu \cdot T$ with the abbreviations $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$:
- $$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$
- $$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 \cdot \big [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3) \big ], $$
- $$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 \cdot \big [g_m(1)+g_m(3)\big ]+ k_2 \cdot \big [g_m(2)+g_m(4)\big ] \hspace{0.05cm}. $$
From this system with three linearly independent equations, one can determine the filter coefficients $k_0$, $k_1$ and $k_2$ in such a way that the basic detection pulse $g_d(t)$ has the following interpolation points:
- $$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} \text{...}$$
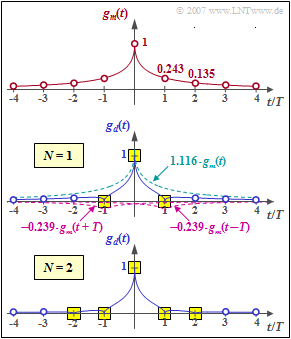
$\text{Example 1:}$ We assume the symmetrical input signal according to the upper diagram in the graph. With the abbreviation $g_m(\nu)= g_m(\pm \nu \cdot T)$ there are the following samples at the distance of the symbol duration $T$:
- $$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= 0.243,\hspace{0.35cm}g_m(2)= 0.135,\hspace{0.35cm}g_m(3)= 0.086, \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$
⇒ For the output pulse $g_d(t =0) = 1$ and $g_d(t =\pm T) = 0$ should be valid. For this purpose, a first-order delay filter with coefficients $k_0$ and $k_1$ is suitable, which must satisfy the following conditions:
- $$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{k_1} = -0.214 \cdot {k_0}\hspace{0.05cm},$$
- $$ t = 0 \hspace{-0.1cm} : \hspace{0.6cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243= 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm}0.896 \cdot {k_0} = 1 \hspace{0.05cm}.$$
From this, the optimal filter coefficients $k_0 = 1.116$ and $k_1 = 0.239$ are obtained.
- The middle diagram shows that thus the first precursor and the first trailer can be compensated and at the same time $g_d(0) =1$ is valid (yellow background).
- However, the further basic detection pulse values (blue circles) are different from zero and cause intersymbol interference.
⇒ The lower diagram shows that with a second order filter $(N = 2)$ zero crossings are forced at $\pm T$ and at $\pm 2T$ if the coefficients $k_0 = 1.127$, $k_1 = 0.219$ and $k_2 = 0.075$ are suitably chosen. The system of equations for determining the optimal coefficients is thereby:
- $$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$
- $$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000+0.135 \big ]+ k_2 \cdot \big [0.243+0.086 \big ] = 0\hspace{0.05cm},$$
- $$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot \big [0.243+0.086\big ]+ k_2 \cdot \big [1.000 + 0.059 \big ]= 0 \hspace{0.05cm}.$$
$\text{Conclusion:}$ The results can be generalized as follows:
- With an $N$–th order delay filter, the main value can be made to $g_d(0)=1$ (normalized).
- The first $N$ trailers $g_{\nu}$ and the first $N$ precursors $g_{-\nu}$ can be made to zero.
- Further precursors and trailers $(\nu \gt N)$ cannot be compensated in this way.
- It is even possible that the precursors and trailers outside the compensation range are enlarged or even new ones are created.
- In the limit $N \to \infty$ (in practice this means: a filter with very many coefficients) a complete Nyquist equalization and thus an ISI-free transmission is possible.
Description in the frequency domain
The fact that the optimal Nyquist equalizer is multiplicatively derived from
- the matched filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – i.e. matched to the basic receiver pulse $g_r(t)$ – and
- a transversal filter $H_{\rm MF}(f)$ with infinitely many filter coefficients
follows from the first Nyquist criterion. By applying the "Calculus of Variations", the frequency response of the transversal filter is obtained – see [TS87][1]:
$$H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - \frac{\kappa}{T}) |^2},$$ $$\text{where }H_{\rm SK}(f) = H_{\rm S}(f)\cdot H_{\rm K}(f).$$
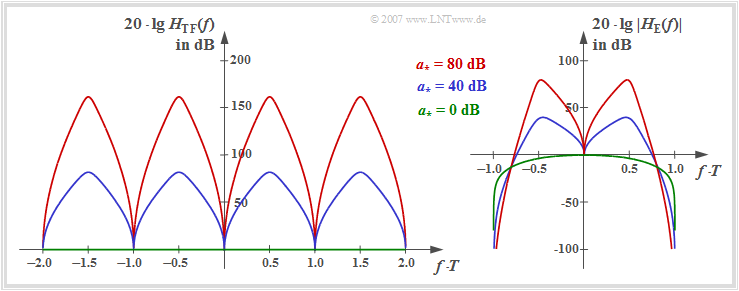
The left graph shows $20 \cdot \lg \ H_{\rm TF}(f)$ in the range $| f | \le 1/T$. This assumes rectangular NRZ transmission pulses and a coaxial cable with the characteristic cable attenuation $a_\star$.
One can see from the equation and the left graph:
- $H_{\rm TF}(f)$ is "real", which results in the symmetrical structure of the transversal filter: $k_{-\lambda} =k_{+\lambda} $.
- $H_{\rm TF}(f)$ is at the same time "periodic" with frequency $1/T$.
- The coefficients are thus obtained from the "Fourier series" (applied to the spectral function):
- $$k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2} \hspace{0.2cm} {\rm d} f$$
- $$ \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = \sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.$$
The right graph shows the frequency response $20 \cdot \lg \ |H_{\rm E}(f)|$ of the entire receiver filter including the matched filter. It holds:
- $$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}.$$
To these representations it is to be noted:
- For $a_\star = 0 \ \rm dB$ (ideal channel, green zero line) the transversal filter $H_{\rm TF}(f)$ can be omitted and it is valid for NRZ rectangular pulses as already derived in the section "Optimal binary receiver – "Matched Filter" realization":
- $$H_{\rm E}(f) =H_{\rm S}(f) = {\rm sinc} (f T).$$
- While the transversal filter frequency response $H_{\rm TF}(f)$ is symmetrical to the Nyquist frequency $f_{\rm Nyq} = 1/(2T)$ at $a_\star \ne 0 \ \rm dB$, this symmetry is no longer given for the receiver filter overall frequency response $H_{\rm E}(f)$.
- The maxima of the frequency responses $H_{\rm TF}(f)$ and $|H_{\rm E}(f)|$ depend significantly on the characteristic cable attenuation $a_\star$. From the blue and red function curves, respectively, can be read:
- $$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)| \ \big] \approx 40\,{\rm dB}\hspace{0.05cm},$$
- $$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big] \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)|\ \big] \approx 80\,{\rm dB}\hspace{0.05cm}.$$
Approximation of the optimal Nyquist equalizer
We now consider the overall frequency response between the Dirac source and the decision.
- This is made up multiplicatively of the frequency responses of the transmitter, channel and receiver.
- According to the derivation, the overall frequency response must satisfy the Nyquist condition:
- $$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = \frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}\hspace{0.05cm}.$$
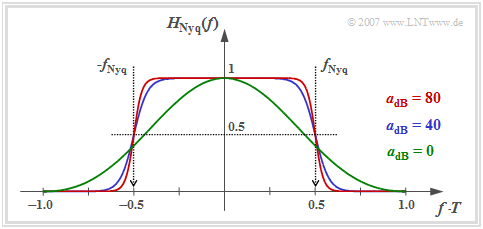
The graph shows the following properties of the optimal Nyquist equalizer $\rm (ONE)$:
- If the cable attenuation is sufficiently large $(a_\star \ge 10 \ \rm dB)$, the overall frequency response can be described with good approximation by the "cosine rolloff low-pass".
- The larger $a_\star$ is, the smaller is the rolloff factor $r$ and the steeper is the edge drop. For the characteristic cable attenuation $a_\star = 40 \ \rm dB$ (blue curve) we get $r \approx 0.4$, for $a_\star = 80 \ \rm dB$ (red curve) $r \approx 0.18$.
- Above the frequency $f_{\rm Nyq} \cdot (1 + r)$, $H_{\rm Nyq}(f)$ has no components. However, with ideal channel ⇒ $a_\star = 0 \ \rm dB$ (green curve), $H_{\rm Nyq}(f)= {\rm sinc}^2(f T)$ theoretically extends to infinity.
The interactive applet "Frequency & Impulse Responses" illustrates, among other things, the properties of the "cosine rolloff low–pass".
Calculation of the normalized noise power
We now consider the (normalized) noise power at the decision. For this holds:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ (2T)} =T \cdot \int_{-1/(2T)}^{+1/(2T)} |H_{\rm E}(f)|^2 \,{\rm d} f .$$
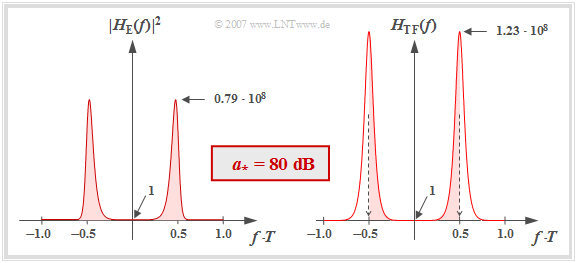
- The left plot shows $|H_{\rm E}(f)|^2$ in linear scale for the characteristic cable attenuation $a_\star = 80 \ \rm dB$. Note that $|H_{\rm E}(f = 0)|^2 = 1$.
- Since the frequency has been normalized to $1/T$ in this plot, the normalized noise power corresponds exactly to the area (highlighted in red) under this curve. The numerical evaluation results in:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = 1.68 \cdot 10^7\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 \approx 72.25\,{\rm dB} \hspace{0.05cm}.$$
- It can be shown that the normalized noise power can be calculated using the transversal filter frequency response $H_{\rm TF}(f)$ alone, as shown in the right graph:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f \hspace{0.3cm}(= k_0)\hspace{0.05cm}.$$
- The red areas are exactly the same in both images.
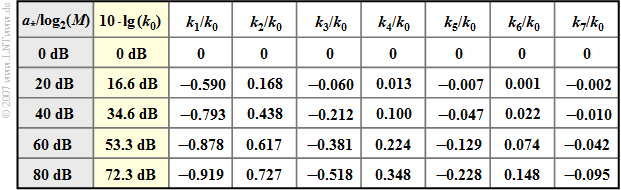
$\text{Conclusion:}$ The normalized noise power of the optimal Nyquist equalizer is equal to the Fourier coefficient $k_0$ when the real, symmetric, and periodic transversal filter frequency response $H_{\rm TF}(f)$ is represented as a Fourier series.
- In the second column of the table, $10 \cdot \lg \ (k_0)$ is given depending on the characteristic cable attenuation $a_\star$ of a coaxial cable.
- Due to the chosen normalization, the table is also valid for "redundancy-free multi-level systems"; here $M$ denotes the level number.
- The coefficients $k_1$, $k_2$, $k_3$, ... of the transversal filter have alternating signs for $a_\star \ne 0 \ \rm dB$.
- For $a_\star = 40 \ \rm dB$, four coefficients are greater in magnitude than $k_0/10$, and for $a_\star = 80 \ \rm dB$ even seven.
Comparison based on the system efficiency
For a system comparison, the "system efficiency" is suitable, which relates the achievable detection SNR $\rho_d$ to the maximum SNR $\rho_{d, \ {\rm max}}$, which, however, is only achievable for ideal channel $H_{\rm K}(f) \equiv 1$.
For the system efficiency, with $M$–level transmission and optimal Nyquist equalization:
- $$\eta = \frac{\rho_d}{s_0^2 \cdot T / N_0}=\frac{{\rm log_2}\hspace{0.1cm}M}{(M-1)^2 \cdot k_0}.$$
- The (normalized) noise power $k_0$ can be read from the table in the last section.
- Note the normalization of the characteristic cable attenuation $a_\star$ in the first column.
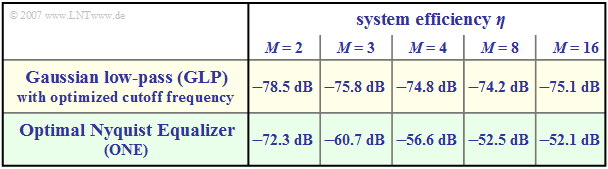
- The table on the right from [TS87][1] allows a system comparison for the characteristic cable attenuation $a_\star = 80 \ \rm dB$.
Compared are:
- the "Gaussian overall frequency response" $\text{(GLP)}$, which leads to an intersymbol interference system even when optimized,
- the "optimal Nyquist equalizer" $\text{(ONE)}$; here, intersymbol interference is excluded per se.
$\text{Conclusion:}$ The results of this system comparison can be summarized as follows:
- In the binary case $(M = 2)$, the intersymbol interference-free system $\text{(ONE)}$ outperforms the intersymbol interference system $\text{(GLP)}$ by about $6 \ \rm dB$.
- If the optimal Nyquist equalization is applied to multi-level systems, a further, significant gain in signal-to-noise ratio is possible compared to $\text{GLP}$.
- For $M =4$, this gain is about $18.2 \ \rm dB$.
- However, the narrowband $\text{GLP}$ system can be significantly improved by using a receiver with decision feedback. This will be discussed in the next chapter.
⇒ At this point we refer to the (German language) SWF applet "Lineare Nyquistentzerrung" ⇒ "Linear Nyquist Equalization".
Exercises for the chapter
Exercise 3.6: Transversal Filter of the Optimal Nyquist Equalizer
Exercise 3.6Z: Optimum Nyquist Equalizer for Exponential Pulse
Exercise 3.7: Optimal Nyquist Equalization once again
Exercise 3.7Z: Regenerator Field Length
References