Difference between revisions of "Modulation Methods/General Description of OFDM"
| (7 intermediate revisions by 2 users not shown) | |||
| Line 13: | Line 13: | ||
| − | *In OFDM, the subcarriers themselves are usually modulated by conventional [[Modulation_Methods/Quadratur–Amplitudenmodulation|quadrature amplitude modulation]] $\rm (QAM)$ or by [[Modulation_Methods/Lineare_digitale_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|binary phase modulation]] $\rm (BPSK)$, although the individual carriers may well differ in terms of the modulation type. | + | *In OFDM, the subcarriers themselves are usually modulated by conventional [[Modulation_Methods/Quadratur–Amplitudenmodulation|$\text{quadrature amplitude modulation}$]] $\rm (QAM)$ or by [[Modulation_Methods/Lineare_digitale_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|$\text{binary phase modulation}$]] $\rm (BPSK)$, although the individual carriers may well differ in terms of the modulation type. |
| Line 22: | Line 22: | ||
*The $N–1$ parts of the data stream $〈q_{\mu,k}〉$ present at time $k$ are first 4-QAM encoded by combining two bits at a time. | *The $N–1$ parts of the data stream $〈q_{\mu,k}〉$ present at time $k$ are first 4-QAM encoded by combining two bits at a time. | ||
*Then the generally complex amplitude $a_{\mu,\hspace{0.08cm}k}$ $($with control variables $\mu = 1$, ... , $N–1)$ is pulse-shaped and modulated with the $\mu$–th multiple of the basic frequency $f_0$. | *Then the generally complex amplitude $a_{\mu,\hspace{0.08cm}k}$ $($with control variables $\mu = 1$, ... , $N–1)$ is pulse-shaped and modulated with the $\mu$–th multiple of the basic frequency $f_0$. | ||
| − | *The transmitted signal is now the additive superposition of the individual partial signals. The consideration takes place here and also in the following in the [[Signal_Representation/Equivalent_Low-Pass_Signal_and_its_Spectral_Function|equivalent low-pass range]], whereby the index "TP" (German: "Tiefpassbereich") is renounced. | + | *The transmitted signal is now the additive superposition of the individual partial signals. The consideration takes place here and also in the following in the [[Signal_Representation/Equivalent_Low-Pass_Signal_and_its_Spectral_Function|$\text{equivalent low-pass range}$]], whereby the index "TP" (German: "Tiefpassbereich") is renounced. |
*The pulse shape filter $g_s(t)$ is a rectangle of height $s_0$ limited to the range $0 ≤ t < T$. | *The pulse shape filter $g_s(t)$ is a rectangle of height $s_0$ limited to the range $0 ≤ t < T$. | ||
| − | *We call $T$ the '''symbol duration''' and denote the reciprocal $f_0 = 1/T$ as the '''basic frequency'''. | + | *We call $T$ the »'''symbol duration'''« and denote the reciprocal $f_0 = 1/T$ as the »'''basic frequency'''«. |
If we now summarize this filter with the respective modulation to | If we now summarize this filter with the respective modulation to | ||
:$$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm otherwise} \\ \end{array} \right.$$ | :$$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm otherwise} \\ \end{array} \right.$$ | ||
| − | with $\mu ∈ \{0, \ \text{...}\ , N–1\}$, we obtain the '''OFDM transmitted signal $s_k(t)$ in the $k$–th time interval''': | + | with $\mu ∈ \{0, \ \text{...}\ , N–1\}$, we obtain the »'''OFDM transmitted signal $s_k(t)$ in the $k$–th time interval'''«: |
:$$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )}.$$ | :$$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )}.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | The total '''OFDM transmitted signal considering all time intervals''' is then: | + | The total »'''OFDM transmitted signal considering all time intervals'''« is then: |
:$$s(t) = \sum\limits_{k = - \infty }^{+\infty} {\sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R} } )} }.$$ | :$$s(t) = \sum\limits_{k = - \infty }^{+\infty} {\sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R} } )} }.$$ | ||
*$T_{\rm R}$ denotes the frame (German: "Rahmen" ⇒ subscript "R") duration. Within this time the same data is present at the input and after $T_{\rm R}$ the next frame follows. | *$T_{\rm R}$ denotes the frame (German: "Rahmen" ⇒ subscript "R") duration. Within this time the same data is present at the input and after $T_{\rm R}$ the next frame follows. | ||
| Line 48: | Line 48: | ||
*The symbol duration in the single carrier $($ $\rm SC)$ case is then: | *The symbol duration in the single carrier $($ $\rm SC)$ case is then: | ||
:$$T_\text{SC} = 1 \cdot {\rm{log}_2}(4) \cdot 1.3 \,{\rm{µ s} } \approx 2.6 \,{\rm{µ s} }.$$ | :$$T_\text{SC} = 1 \cdot {\rm{log}_2}(4) \cdot 1.3 \,{\rm{µ s} } \approx 2.6 \,{\rm{µ s} }.$$ | ||
| − | *Assuming that for a | + | *Assuming that for a multicarrier $($ $\rm MC)$ system with $N = 32$ carriers the modulation method $\text{16–QAM}$ is used, the symbol duration is larger by a factor of $64$: |
:$$T_\text{MC} = 32 \cdot {\rm{log}_2}(16) \cdot 1.3 \,{\rm{µ s} } \approx 0.167\, {\rm{ms} }.$$ }} | :$$T_\text{MC} = 32 \cdot {\rm{log}_2}(16) \cdot 1.3 \,{\rm{µ s} } \approx 0.167\, {\rm{ms} }.$$ }} | ||
| Line 56: | Line 56: | ||
*The duration of a symbol increases significantly for a multicarrier system compared to a single-carrier system, reducing the spurious influence of the channel impulse response and decreasing intersymbol interference. | *The duration of a symbol increases significantly for a multicarrier system compared to a single-carrier system, reducing the spurious influence of the channel impulse response and decreasing intersymbol interference. | ||
| − | *The ability to use different robust modulation schemes for different subbands is one of the '''major advantages of OFDM'''. This will be discussed in more detail in the following sections [[Modulation_Methods/OFDM_für_4G–Netze|OFDM for 4G networks]] and [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_DSL|Digital Subscriber Line]] $\rm (DSL)$. }} | + | *The ability to use different robust modulation schemes for different subbands is one of the »'''major advantages of OFDM'''«. This will be discussed in more detail in the following sections [[Modulation_Methods/OFDM_für_4G–Netze|"OFDM for 4G networks"]] and [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_DSL|"Digital Subscriber Line"]] $\rm (DSL)$. }} |
| Line 67: | Line 67: | ||
For simplicity, we assume the basic pulse $g_{\mu}(t)$ to be symmetric at $t = 0$. Then it is valid with $f_0 = 1/T$: | For simplicity, we assume the basic pulse $g_{\mu}(t)$ to be symmetric at $t = 0$. Then it is valid with $f_0 = 1/T$: | ||
:$$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad \quad - T/2 < t < T/2, \\ 0 \quad \quad \quad \quad \quad \quad \; {\rm otherwise.} \\ \end{array} \right.$$ | :$$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad \quad - T/2 < t < T/2, \\ 0 \quad \quad \quad \quad \quad \quad \; {\rm otherwise.} \\ \end{array} \right.$$ | ||
| − | In the spectral domain, such an acausal rectangular function modulated by a (complex) exponential function of frequency $\mu · f_0$ corresponds to | + | In the spectral domain, such an acausal rectangular function modulated by a (complex) exponential function of frequency $\mu · f_0$ corresponds to a $\rm sinc$ function shifted by $\mu · f_0$: |
:$$G_\mu (f) = s_0 \cdot T \cdot {\rm{sinc}} \big((f - \mu f_0 )\cdot T \big ).$$ | :$$G_\mu (f) = s_0 \cdot T \cdot {\rm{sinc}} \big((f - \mu f_0 )\cdot T \big ).$$ | ||
On the right, this spectral function $($normalized to the maximum $s_0 · T)$ is shown for $\mu = 5$. – The arrow is to suggest that if the basic pulse is unconstrained in time, the $\rm sinc$ function shown would have to be replaced by a Dirac delta function at $\mu · f_0$. | On the right, this spectral function $($normalized to the maximum $s_0 · T)$ is shown for $\mu = 5$. – The arrow is to suggest that if the basic pulse is unconstrained in time, the $\rm sinc$ function shown would have to be replaced by a Dirac delta function at $\mu · f_0$. | ||
| Line 91: | Line 91: | ||
The diagram shows an example of the magnitude spectrum of an OFDM signal with five carriers. | The diagram shows an example of the magnitude spectrum of an OFDM signal with five carriers. | ||
| − | [[File: | + | [[File:ENneu_Mod_T_5_5_S4_v2.png|right|frame| Spectrum of an OFDM signal]] |
*It is remarkable that the maximum of each subcarrier coincides with the zeros of all other carriers. This corresponds to the first Nyquist condition in the frequency domain. | *It is remarkable that the maximum of each subcarrier coincides with the zeros of all other carriers. This corresponds to the first Nyquist condition in the frequency domain. | ||
| Line 101: | Line 101: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Conclusion:}$ An OFDM signal under the condition of a rectangular pulse shaping and a subcarrier spacing of $f_0$ | $\text{Conclusion:}$ An OFDM signal under the condition of a rectangular pulse shaping and a subcarrier spacing of $f_0$ | ||
| − | *fulfills the [[Digital_Signal_Transmission/ | + | *fulfills the [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_time_domain|$\text{first Nyquist condition in the time domain}$]] and thus, of course, |
| − | *also the [[Digital_Signal_Transmission/ | + | *also the [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_frequency_domain |$\text{first Nyquist condition in the frequency domain}$]].}} |
| Line 111: | Line 111: | ||
Here, the $k$–th transmitted pulse | Here, the $k$–th transmitted pulse | ||
*is the sum of the basic pulses $g_{\mu}(t)$ shifted by $k · T$, | *is the sum of the basic pulses $g_{\mu}(t)$ shifted by $k · T$, | ||
| − | *each of which is weighted by the $\mu$–th amplitude coefficients of the QAM | + | *each of which is weighted by the $\mu$–th amplitude coefficients of the QAM encoder at time $k$. |
| Line 161: | Line 161: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ The '''orthogonality of the OFDM signal''' $s(t)$ | + | $\text{Conclusion:}$ The »'''orthogonality of the OFDM signal'''« $s(t)$ |
*is given for the control variable $k$ $\rm (time)$ | *is given for the control variable $k$ $\rm (time)$ | ||
*as well as for the control variable $\mu$ $\text{(carrier frequencies)}$ !}} | *as well as for the control variable $\mu$ $\text{(carrier frequencies)}$ !}} | ||
Latest revision as of 17:31, 23 January 2023
Contents
The principle of OFDM - system consideration in the time domain
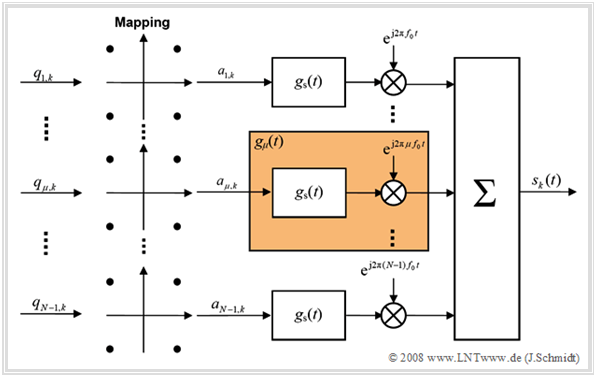
Orthogonal Frequency Division Multiplex $\rm (OFDM)$ is a digital multicarrier modulation method with the following characteristics:
- Instead of a broadband, strongly modulated signal, a large number of narrowband, mutually orthogonal subcarriers are used for data transmission. Among other things, this enables adaptation to a frequency-selective channel.
- In OFDM, the subcarriers themselves are usually modulated by conventional $\text{quadrature amplitude modulation}$ $\rm (QAM)$ or by $\text{binary phase modulation}$ $\rm (BPSK)$, although the individual carriers may well differ in terms of the modulation type.
- Differences in the degree of modulation result in different data rates for the subcarriers. This means that a high-rate source signal must be split into several signals of significantly lower symbol rate for transmission.
The diagram shows the principle of an OFDM transmitter based on the modulation method $\text{4-QAM}$.
- The representation of the "zeroth" branch $(\mu = 0)$, which represents the DC part, has been deliberately omitted here because it is often set to zero ⇒ for all frames $k$ ⇒ $a_{0,\hspace{0.08cm} k} =0 $ holds.
- The $N–1$ parts of the data stream $〈q_{\mu,k}〉$ present at time $k$ are first 4-QAM encoded by combining two bits at a time.
- Then the generally complex amplitude $a_{\mu,\hspace{0.08cm}k}$ $($with control variables $\mu = 1$, ... , $N–1)$ is pulse-shaped and modulated with the $\mu$–th multiple of the basic frequency $f_0$.
- The transmitted signal is now the additive superposition of the individual partial signals. The consideration takes place here and also in the following in the $\text{equivalent low-pass range}$, whereby the index "TP" (German: "Tiefpassbereich") is renounced.
- The pulse shape filter $g_s(t)$ is a rectangle of height $s_0$ limited to the range $0 ≤ t < T$.
- We call $T$ the »symbol duration« and denote the reciprocal $f_0 = 1/T$ as the »basic frequency«.
If we now summarize this filter with the respective modulation to
- $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm otherwise} \\ \end{array} \right.$$
with $\mu ∈ \{0, \ \text{...}\ , N–1\}$, we obtain the »OFDM transmitted signal $s_k(t)$ in the $k$–th time interval«:
- $$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )}.$$
The total »OFDM transmitted signal considering all time intervals« is then:
- $$s(t) = \sum\limits_{k = - \infty }^{+\infty} {\sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T_{\rm{R} } )} }.$$
- $T_{\rm R}$ denotes the frame (German: "Rahmen" ⇒ subscript "R") duration. Within this time the same data is present at the input and after $T_{\rm R}$ the next frame follows.
- For a multicarrier system with $M$ QAM signal space points and the bit duration $T_{\rm B}$ of the binary source symbols, the symbol duration $T$ is generally given by
- $$T = N \cdot {\rm{log}_2}(M) \cdot T_{\rm{B} } ,$$
- where $N$ is again the number of subcarriers.
- For the frame duration, $T_{\rm R} \ge T$ must hold. Initially, let $T_{\rm R} = T$.
$\text{Example 1:}$
- We first assume a single-carrier system with data rate $R_{\rm B} = 768 \ \rm kbit/s$ ⇒ $T_{\rm B} ≈ 1.3 \ \rm µ s$ and a mapping with $M = 4$ signal space points $\text{(4–QAM)}$.
- The symbol duration in the single carrier $($ $\rm SC)$ case is then:
- $$T_\text{SC} = 1 \cdot {\rm{log}_2}(4) \cdot 1.3 \,{\rm{µ s} } \approx 2.6 \,{\rm{µ s} }.$$
- Assuming that for a multicarrier $($ $\rm MC)$ system with $N = 32$ carriers the modulation method $\text{16–QAM}$ is used, the symbol duration is larger by a factor of $64$:
- $$T_\text{MC} = 32 \cdot {\rm{log}_2}(16) \cdot 1.3 \,{\rm{µ s} } \approx 0.167\, {\rm{ms} }.$$
$\text{Conclusions:}$
- The duration of a symbol increases significantly for a multicarrier system compared to a single-carrier system, reducing the spurious influence of the channel impulse response and decreasing intersymbol interference.
- The ability to use different robust modulation schemes for different subbands is one of the »major advantages of OFDM«. This will be discussed in more detail in the following sections "OFDM for 4G networks" and "Digital Subscriber Line" $\rm (DSL)$.
System consideration in the frequency domain with acausal basic pulse
We consider again the OFDM transmitted signal in the $k$–th time interval with setting $T_{\rm R} = T$:
- $$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T)}.$$
For simplicity, we assume the basic pulse $g_{\mu}(t)$ to be symmetric at $t = 0$. Then it is valid with $f_0 = 1/T$:
- $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad \quad - T/2 < t < T/2, \\ 0 \quad \quad \quad \quad \quad \quad \; {\rm otherwise.} \\ \end{array} \right.$$
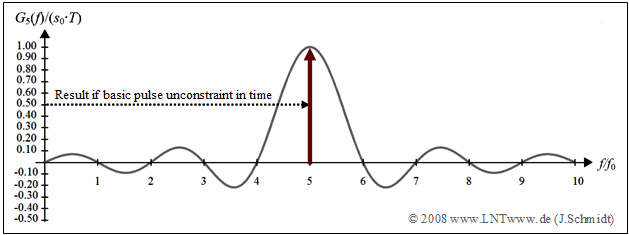
In the spectral domain, such an acausal rectangular function modulated by a (complex) exponential function of frequency $\mu · f_0$ corresponds to a $\rm sinc$ function shifted by $\mu · f_0$:
- $$G_\mu (f) = s_0 \cdot T \cdot {\rm{sinc}} \big((f - \mu f_0 )\cdot T \big ).$$
On the right, this spectral function $($normalized to the maximum $s_0 · T)$ is shown for $\mu = 5$. – The arrow is to suggest that if the basic pulse is unconstrained in time, the $\rm sinc$ function shown would have to be replaced by a Dirac delta function at $\mu · f_0$.
$\text{Conclusions:}$ If all amplitude coefficients $a_{μ,\hspace{0.08cm}k} ≠ 0$, the spectrum $S_k(f)$ of the transmitted signal in the $k$–th time domain interval
- is composed of $N$ $\rm sinc$ functions ⇒ ${\rm sinc}(x) = \sin(\pi x)/(\pi x),$
- each shifted by a multiple of the basic frequency $f_0$.
System consideration in the frequency domain with causal basic pulse
$\text{Important result:}$
- If one also takes into account that in reality a causal basic pulse
- $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e} }^{ {\kern 1pt} {\rm{j{\kern 1pt}\cdot {\kern 1pt}2 \pi} } {\kern 1pt}\cdot {\kern 1pt} \mu f_0 {\kern 1pt}\cdot {\kern 1pt}t} \quad 0 \le t < T, \\ 0\quad \quad \quad \quad \quad \quad {\rm otherwise}, \\ \end{array} \right.$$
- has to be assumed, the spectrum is given by
- $$S_k (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot \,} {\rm{sinc} }\big( (f - \mu \cdot f_0 )\cdot T\big) \cdot {\rm{e} }^{ - {\rm{j{\kern 1pt}\cdot {\kern 1pt}2\pi} }\hspace{0.05cm}\cdot \hspace{0.05cm} {T}/{2} \hspace{0.05cm}\cdot \hspace{0.05cm} (f - \mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_0 )} .$$
- The complex exponential function comes from the limits of the rectangle used here for pulse shaping in the time domain $0$ ... $T$ $($shift by $T/2)$.
- The purely real $\rm sinc$ function shown before, on the other hand, would correspond to the non-causal rectangle of $ -T/2$ ... $+T/2$.
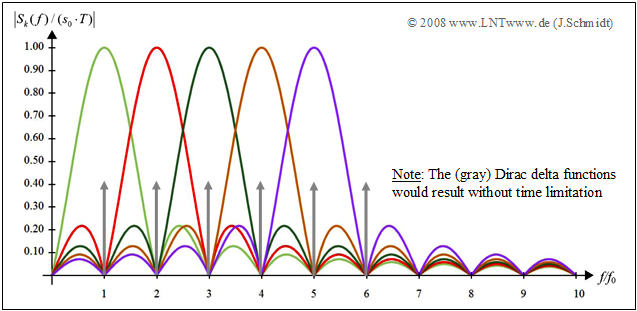
The diagram shows an example of the magnitude spectrum of an OFDM signal with five carriers.
- It is remarkable that the maximum of each subcarrier coincides with the zeros of all other carriers. This corresponds to the first Nyquist condition in the frequency domain.
- This property allows "ICI"–free sampling (that is: without intercarrier interference) of the spectrum at multiples of $f_0$. Orthogonality is therefore guaranteed.
- If one were to dispense with the time limit in pulse shaping, the displayed $\rm sinc$ functions would each become Dirac delta lines at the distance $f_0$ (drawn in gray in the diagram).
- This idealizing simplification is unfortunately not realizable in practice. Indeed, the requirement $T → ∞$ means at the same time that only one frame could be transmitted in an infinitely long time.
$\text{Conclusion:}$ An OFDM signal under the condition of a rectangular pulse shaping and a subcarrier spacing of $f_0$
- fulfills the $\text{first Nyquist condition in the time domain}$ and thus, of course,
- also the $\text{first Nyquist condition in the frequency domain}$.
Orthogonality properties of the carriers
The time limit of the basic pulse allows the separate consideration of the two sums in the equation of the OFDM transmitted signal:
- $$s(t) = \sum\limits_{k = - \infty }^{+\infty} {s_k (t)} \quad {\rm{with}} \quad s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,\hspace{0.08cm}k} \cdot g_\mu (t - k \cdot T )}.$$
Here, the $k$–th transmitted pulse
- is the sum of the basic pulses $g_{\mu}(t)$ shifted by $k · T$,
- each of which is weighted by the $\mu$–th amplitude coefficients of the QAM encoder at time $k$.
$\text{Another important result:}$
This gives for the spectrum $S_{\mu,\hspace{0.08cm}k}(f)$ of the $\mu$–th carrier in the $k$–th interval:
- $$S_{\mu ,\hspace{0.08cm}k} (f) = s_0 \cdot a_{\mu ,\hspace{0.08cm}k} \cdot T \cdot {\rm{sinc} }\big( (f - \mu \cdot f_0 )\cdot T\big) \cdot {\rm{e} }^{ - {\rm{j \hspace{0.05cm} \cdot \hspace{0.05cm} \pi} } \hspace{0.05cm} \cdot \hspace{0.05cm}T \hspace{0.05cm} \cdot \hspace{0.05cm} (f - \mu \hspace{0.05cm} \cdot \hspace{0.05cm} f_0)}.$$
The following properties, which are important for the OFDM principle, apply:
- The $s_k(t)$ are orthogonal to each other in time $($control variable $k)$, since they do not overlap in time due to the time limitation of the pulse shape filter $g_s(t)$.
- Although the time limitation of the pulses leads to a spectral overlap, there is nevertheless also orthogonality with respect to the carriers $($control variable $\mu)$, since:
- $$S_k (\mu \cdot f_0 ) = S_{\mu ,\hspace{0.08cm}k} (\mu \cdot f_0 ) = s_0 \cdot a_{\mu ,\hspace{0.08cm}k} \cdot T.$$
$\text{Proof:}$ For orthogonality at the frequency support points $\mu · f_0$ must hold:
- $$S(\mu \cdot f_0 ) = S_0 (\mu \cdot f_0 ) + \ \text{...} \ + S_\mu (\mu \cdot f_0 ) + \ \text{...} \ + S_{N - 1} (\mu \cdot f_0 ) = S_\mu (\mu \cdot f_0 ).$$
- Here and in the following, we omit the index $k$ of the frame number. From
- $$s_\mu (t) = s_0 \cdot a_\mu \cdot {\rm{e} }^{{\rm j \hspace{0.03cm}\cdot\hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm} \mu \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{rect} } \left( {\frac{ {t - T/2} }{T} } \right) \hspace{0.45cm} {\rm{and }} \hspace{0.45cm} S_\mu (f) = \int_{ - \infty }^{+\infty} {s_\mu (t) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t}$$
- the spectrum $S(f)$ results in general to:
- $$S(f) = \left( {s_0 \cdot a_0 \cdot T \cdot {\rm{sinc} }(f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}/{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \int_{ - \infty }^{+\infty} { {\rm{e} }^{\rm{0} } \cdot {\rm{e} }^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} \hspace{0.08cm}+ \text{...} $$
- $$\hspace{0.5cm}\text{...} + \left( {s_0 \cdot a_\mu \cdot T \cdot {\rm{sinc} } ( f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm}{T}/{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \int_{ - \infty }^{+\infty} { {\rm{e} }^{ {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm}\mu \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{e} }^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} \hspace{0.08cm}+ \text{...} $$
- $$ \hspace{0.5cm}\text{...} +\left( {s_0 \cdot a_{N - 1} \cdot T \cdot {\rm{sinc} } ( f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}/{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} }\right) * \int_{ - \infty }^{+\infty} { {\rm{e} }^{ {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm}(N-1) \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{e} }^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} .$$
- With distributions, this equation can be expressed as follows:
- $$S(f) = \left( {s_0 \cdot a_0 \cdot T \cdot {\rm{sinc} }(f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \delta (f) \hspace{0.08cm}+ \text{...} $$
- $$\hspace{0.5cm} \text{...} + \left( {s_0 \cdot a_\mu \cdot T \cdot {\rm{sinc} } ( fT )\cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \delta (f - \mu \cdot f_0 )\hspace{0.08cm}+ \text{...} $$
- $$\hspace{0.5cm} \text{...} + \left( {s_0 \cdot a_{N - 1} \cdot T \cdot {\rm{sinc} } ( f T ) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} }\right) * \delta (f-(N - 1) \cdot f_0 ) .$$
- $$\Rightarrow \hspace{0.3cm}S(f) = {s_0 \cdot a_0 \cdot T \cdot {\rm{sinc} }( T \cdot f) \cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \hspace{0.08cm}+\hspace{0.08cm} \text{...} $$
- $$\hspace{1.4cm}\text{...} + {s_0 \cdot a_\mu \cdot T \cdot {\rm{sinc} } ( T \cdot (f - \mu \cdot f_0 ))\cdot {\rm{e} }^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} (f - \mu \hspace{0.03cm}\cdot \hspace{0.03cm}f_0 )} } \hspace{0.08cm}+ \hspace{0.08cm}\text{...}$$
- $$ \hspace{1.4cm}\text{...} + s_0 \cdot a_{N - 1} \cdot T \cdot {\rm sinc } ( T \cdot \big [f-(N - 1) \cdot f_0 ) \big ] \cdot {\rm e}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\hspace{0.03cm}\cdot \hspace{0.03cm} \big [f-(N - 1) \hspace{0.03cm}\cdot \hspace{0.03cm}f_0 \big ]}.$$
- Now setting $f = \mu · f_0$, we obtain:
- $$S (\mu \cdot f_0) = 0 \hspace{0.08cm}+ \hspace{0.08cm} \text{...} \hspace{0.08cm}+\hspace{0.08cm} s_0 \cdot a_\mu \cdot T \cdot {\rm{sinc} } (0) \cdot {\rm{e} }^0 \hspace{0.08cm}+\hspace{0.08cm} \text{...}+ 0 = s_0 \cdot a_\mu \cdot T = S_\mu ( \mu \cdot f_0 ).$$
- Thus, the spectrum at $f = \mu · f_0$ is composed only of components of the $\mu$–th carrier, with all other carriers becoming identically zero.
- Orthogonality is guaranteed. q.e.d.
$\text{Conclusion:}$ The »orthogonality of the OFDM signal« $s(t)$
- is given for the control variable $k$ $\rm (time)$
- as well as for the control variable $\mu$ $\text{(carrier frequencies)}$ !
Exercises for the chapter
Exercise 5.6Z: Single and Multiple Beam System