Modulation Methods/Quality Criteria

1. Modulation Methods
2. General Description
3. Quality Criteria

• Previous page
• Next page

• Previous page
• Next page

Ideal Distortionless System

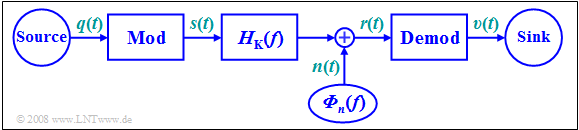
In all subsequent chapters, the following model will be assumed:

Block diagram describing modulation and demodulation

The task of any message transmission system is to provide a signal  $v(t)$  at a spatially distant sink that differs as little as possible from the source signal   $q(t)$ .

$\text{Definition:}$  An  ideal system  is achieved when the following conditions hold:

$$v(t) = q(t) + n(t), \hspace{1cm}n(t) \to 0.$$

This takes into account that  $n(t) \equiv 0$  is physically impossible due to Thermal Noise.

In practice, the  $q(t)$  and  $v(t)$  signals will not differ by more than  $n(t)$  for the following reasons:

• Non-ideal realization of the modulator and demodulator,
• linear attenuation distortions and phase distortions, as well as nonlinearities,
• external disturbances and additional stochastic noise processes,
• frequency-independent damping and delay.

$\text{Definition:}$  A  distortionless system  is achieved, if from the above list only the last restriction is effective:

$$v(t) = \alpha \cdot q(t- \tau) + n(t), \hspace{1cm}n(t) \to 0.$$

• Due to the damping ratio  $α$ , the sink signal  $v(t)$ is only "quieter" compared to the source signal  $q(t)$ .
• Even a delay  $τ$  is often tolerable, at least for a unidirectional transmission.
• In contrast, in bidirectional communications – such as a telephone call – a delay of 300 milliseconds is already perceived as a significant disturbance.

Signal–to–noise power ratio

In the general case, the sink signal  $v(t)$  will still differ from   $α · q(t - τ)$  , and the error signal is characterised by:

$$\varepsilon (t) = v(t) - \alpha \cdot q(t- \tau) = \varepsilon_{\rm V} (t) + \varepsilon_{\rm St} (t).$$

This error signal is composed of two components:

• linear and nonlinear distortions  $ε_{\rm V}(t)$, which are caused by the frequency responses of the modulator, channel, and demodulator and thus exhibit deterministic (time-invariant) behavior;
• a stochastic component $ε_{\rm St}(t)$ , which originates from the RF interference   $n(t)$  at the demodulator input. However, unlike   $n(t)$ ,   $ε_{\rm St}(t)$  is usually a low-frequency noise disturbance.

$\text{Definition:}$  As a measure of the quality of the communication system, the signal-to-noise power ratio  $ρ_v$  at the sink is defined as the quotient of the signal power (variance) of the useful component  $v(t) - ε(t)$  and the interference component  $ε(t)$ , respectively:

$$\rho_{v} = \frac{ P_{v -\varepsilon} }{P_{\varepsilon} } \hspace{0.05cm},\hspace{0.7cm}\text{with}\hspace{0.7cm} P_{v -\varepsilon} = \overline{[v(t)-\varepsilon(t)]^2} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M} } \cdot \int_{0}^{ T_{\rm M} } {\big[v(t)-\varepsilon(t)\big]^2 }\hspace{0.1cm}{\rm d}t,\hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon^2(t)} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M} } \cdot \int_{0}^{ T_{\rm M} } {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t\hspace{0.05cm}.$$

For the power of the useful part, we obtain  $τ$ regardless of the running time :

$$P_{v -\varepsilon} = \overline{\big[v(t)-\varepsilon(t)\big]^2} = \overline{\alpha^2 \cdot q^2(t - \tau)}= \alpha^2 \cdot P_{q}.$$

Here,  $P_q$  denotes the power of the source signal $q(t)$:

$$P_{q} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {q^2(t) }\hspace{0.1cm}{\rm d}t .$$

  This gives:

$$\rho_{v} = \frac{\alpha^2 \cdot P_{q} }{P_{\varepsilon} } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho_{v} = 10 \cdot {\rm lg} \hspace{0.15cm} \frac{\alpha^2 \cdot P_{q} }{P_{\varepsilon} } \hspace{0.05cm}.$$

In the following, we will refer to  $ρ_v$  as the Signal–to–Noise–Ratio (or Sink SNR for short) and  $10 · \lg \ ρ_v$ as the Sink–to-Noise Ratio, which is expressed in dB when using the logarithm of ten   $(\lg)$ .

Zur Verdeutlichung des Fehlersignals

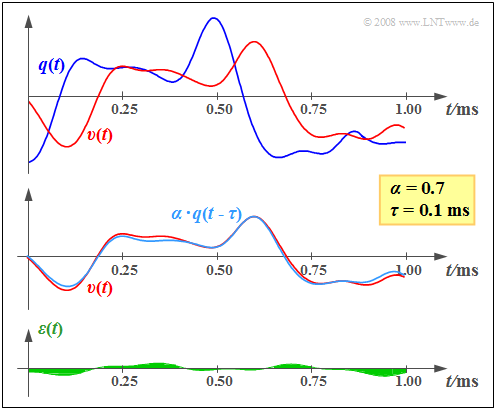
$\text{Example 1:}$  On the right, you can see an exemplary section of the (blue) source signal  $q(t)$  and the (red) sink signal  $v(t)$, which are noticeably different.

However, the middle graph makes it clear that the main difference between  $q(t)$  and  $v(t)$  is due to the damping factor  $α = 0.7$  and the transmission delay  $τ = 0.1\text{ ms}$ 

The bottom sketch shows the remaining error signal  $ε(t) = v(t) - α · q(t - τ)$  after correcting for attenuation and delay.  We refer to the root mean square (variance) of this signal as the noise power  $P_ε$.

To calculate the sink SNR  $ρ_v$ ,  $P_ε$  must be related to the useable signal power  $α^2 · P_q$ . This is obtained from the variance of the signal  $α · q(t - τ)$, plotted in light blue in the middle graph.

From the assumed properties  $\alpha = 0.7$   ⇒   $\alpha^2 \approx 0.5$  as well as  $P_{q} = 8\,{\rm V^2}$  and  ${P_{\varepsilon} } = 0.04\,{\rm V^2}$ , we obtain the sink SNR  $ρ_v ≈ 100$  and the sink-to-noise ratio $10 · \lg ρ_v ≈ 20$ dB.

• The error signal  $ε(t)$  – and thus also the sink SNR  $ρ_v$  – takes into account all imperfections of the message transmission system under consideration (e.g. distortions, external interferences, noise, etc.).
• In the following, we will consider each of these different effects separately for the sake of explanation.

Investigating signal distortion

All modulation methods described in the following chapters lead to distortions under non-ideal conditions, i.e. to a sink signal  $v(t) ≠ α · q(t - τ)$, which differs from  $q(t)$  by more than just damping and delay.  For the study and description of these signal distortions, we always assume the following premises and model:

Simplified model of a communication system

• The additive noise signal  $n(t)$  at the channel output (demodulator input) is negligible and ignored.
• All components of modulator and demodulator are treated as linear,
• Similarly, the channel is assumed linear, and is thus completely characterized by its frequency response  $H_{\rm K}(f)$ .

Depending on the type and realization of modulator and demodulator, the following signal distortions occur:

Linear Disortions, as described in the  chapter of the same name  in the book "Linear and Time-Invariant Systems":

• Linear can generally be compensated by an equalizer, but this will always result in higher interference power and thus lower sink SNR in the presence of a stochastic interference  $n(t)$ .
• These linear distortions can be further divided into attenuation distortions and phase distortions.

Non-linear Distortions, as described in the  chapter of the same name  in the book "Linear and Time-Invariant Systems":

• Nonlinear distortions are irreversible and thus a more severe problem than linear distortions.
• A suitable quantitative measure of such distortions is the distortion factor  $K$, for example, which is related to the sink SNR in the following way:

$$\rho_{v} = {1}/{K^2} \hspace{0.05cm}.$$

• However, specifying a distortion factor assumes a harmonic oscillation as the source signal.

We refer you to three basic tutorial videos:

• Linear and non-linear distortions,
• Properties of the transmission channel,
• Some remarks on the transmission function..

$\text{Two further points:}$

1.   The distortions with respect to  $q(t)$  and  $v(t)$  are nonlinear in nature whenever the channel contains nonlinear components and, as such, nonlinear distortions are already present with respect to the  $s(t)$  and  $r(t)$  signals.
2.   Similarly, nonlinearities in the modulator or demodulator always lead to nonlinear distortions.

Some remarks on the AWGN channel model

To investigate the noise behavior of each individual modulation and demodulation method, the starting point is usually the so-called AWGN channel, where the abbreviation stands for  "$\rm A$dditive $\rm W$hite $\rm G$aussian $\rm N$oise"  and already sufficiently describes the properties of this channel model. We would also like to refer you to the three-part tutorial video  The AWGN Channel.

• The additive noise signal includes all frequency components equally;  $n(t)$  has a constant power density spectrum   $\rm (LDS)$ and a Dirac-shaped autocorrelation function $\rm (ACF)$:

$${\it \Phi}_n(f) = \frac{N_0}{2}\hspace{0.15cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm} \varphi_n(\tau) = \frac{N_0}{2} \cdot \delta (\tau)\hspace{0.05cm}.$$:

In each case, the factor  $1/2$  in these equations accounts for the two-sided spectral representation.

• For example, in the case of thermal noise, for the physical noise power density (from a one-sided view) with a noise value  $F ≥ 1$  and an absolute temperature  $θ$:

$${N_0}= F \cdot k_{\rm B} \cdot \theta , \hspace{0.3cm}k_{\rm B} = 1.38 \cdot 10^{-23}{ {\rm Ws} }/{ {\rm K} }\hspace{0.2cm}{\rm (Boltzmann-Konstante)}\hspace{0.05cm}.$$

• Bei echt weißem Rauschen würde sich eine unendliche große Leistung ergeben.  Deshalb ist stets eine Bandbegrenzung auf  $B$  zu berücksichtigen, und es gilt für die wirksame Rauschleistung:

$$N = \sigma_n^2 = {N_0} \cdot B \hspace{0.05cm}.$$

• Das Störsignal  $n(t)$  besitzt eine Gaußsche Wahrscheinlichkeitsdichtefunktion  $\rm (WDF)$   ⇒ Amplitudenverteilung  mit Störeffektivwert  $σ_n$:

$$f_n(n) = \frac{1}{\sqrt{2\pi}\cdot\sigma_n}\cdot {\rm e}^{-{\it n^{\rm 2}}/{(2\sigma_{\it n}^2)}}.$$

• Eigentlich ist beim AWGN–Kanal  $H_{\rm K}(f) = 1$  zu setzen.  Wir modifizieren dieses Modell für unsere Untersuchungen jedoch in der Form, dass wir eine frequenzunabhängige Dämpfung zulassen  (beachten Sie:  Ein frequenzunabhängiger Dämpfungsfaktor führt ebenfalls nicht zu Verzerrungen):

$$H_{\rm K}(f) = \alpha_{\rm K}= {\rm const.}$$

Untersuchungen beim AWGN–Kanal

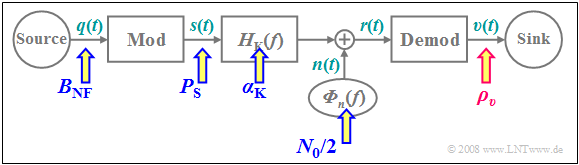
Bei allen Untersuchungen hinsichtlich Rauschverhalten gehen wir vom unten skizzierten Blockschaltbild aus.  Wir werden dabei stets das Sinken–SNR  $ρ_v$  in Abhängigkeit aller Systemparameter berechnen und zu folgenden Ergebnissen kommen:

• Je mehr Sendeleistung  $P_{\rm S}$  aufgewendet wird, desto besser ist das Sinken–SNR  $ρ_v$.  Bei einigen Verfahren ergibt sich sogar ein linearer Zusammenhang.
• $ρ_v$  nimmt mit steigender Rauschleistungsdichte  $N_0$  monoton ab.  Eine Vergrößerung von  $N_0$  kann meist durch eine größere Sendeleistung  $P_{\rm S}$  ausgeglichen werden.
• Je kleiner der Parameter  $α_{\rm K}$  des Kanals ist, um so kleiner wird  $ρ_v$.  Es besteht oft eine quadratische Abhängigkeit, da die Empfangsleistung  $P_{\rm E} = {α_{\rm K}}^2 · P_{\rm S}$  ist.
• Ein breitbandigeres Quellensignal  $($größeres  $B_{\rm NF})$  führt zu kleinerem  $ρ_v$   ⇒   man muss auch die HF–Bandbreite vergrößern   ⇒   mehr werden Störungen wirksam.

Blockschaltbild zur Untersuchung des Rauschverhaltens

$\text{Fazit:}$  Unter Berücksichtigung dieser vier Aussagen kommt man zu dem Schluss, dass es Sinn macht, das Sinken–SNR in der Form

$$\rho_{v } = \rho_{v }(\xi) \hspace{0.5cm} {\rm mit} \hspace{0.5cm}\xi = \frac{ {\alpha_{\rm K} }^2 \cdot P_{\rm S} }{N_0 \cdot B_{\rm NF} }$$

normiert darzustellen.  Im Folgenden bezeichnen wir  $ξ$  als die  Leistungskenngröße.

Die in  $ξ$  zusammengefassten Eingangsgrößen sind in obigem Blockschaltbild mit blauen Pfeilen markiert, während das Qualitätskriterium  $ρ_v$  durch den roten Pfeil hervorgehoben ist.

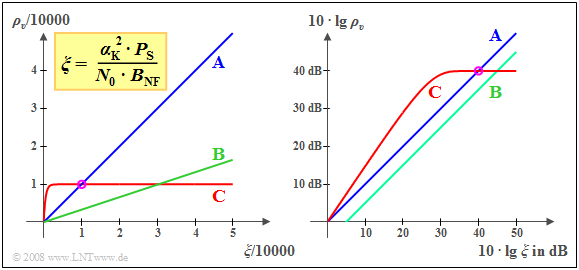
$\text{Beispiel 2:}$  In der linken Grafik ist das Sinken–SNR  $ρ_v$  für drei verschiedene Systeme dargestellt, jeweils in Abhängigkeit von der normierten Leistungskenngröße  

Untersuchungen beim AWGN–Kanal

$$\xi = { {\alpha_{\rm K} }^2 \cdot P_{\rm S} }/({N_0 \cdot B_{\rm NF} }).$$

• Beim  $\text{System A}$  gilt  $ρ_ν = ξ$.  Beispielsweise führen die Systemparameter

$$P_{\rm S}= 10 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 10^{-4}\hspace{0.05cm},$$

$$ {N_0} = 10^{-12}\hspace{0.05cm}{ {\rm W} }/{ {\rm Hz} }\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 10\; {\rm kHz}$$

zu  $ξ = ρ_v = 10000$  (siehe kreisförmige Markierung der Skizze).  Exakt das gleiche Sinken–SNR ergäbe sich mit den Parametern

$$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 10^{-6}\hspace{0.05cm},$$

$${N_0} = 10^{-16}\hspace{0.05cm}{ {\rm W} }/{ {\rm Hz} }\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$

• Auch beim  $\text{System B}$  besteht mit  $ρ_v = ξ/3$  ein linearer Zusammenhang.  Die Gerade geht ebenfalls durch den Nullpunkt.  Die Steigung beträgt aber nur  $1/3$. 

Anzumerken ist, dass ein Rauschverhalten entsprechend  $\text{System A}$  bei  Zweiseitenband–Amplitudenmodulation ohne Träger   ⇒   Modulationsgrad  $m → ∞$  festzustellen ist, während  $\text{System B}$  eine  Zweiseitenband–Amplitudenmodulation mit Träger und Modulationsgrad  $m ≈ 0.5$  beschreibt.

• Das  $\text{System C}$  zeigt ein völlig anderes Rauschverhalten.  Für kleine  $ξ$–Werte ist dieses System dem  $\text{System A}$  überlegen, während für  $ξ = 10000$  die Qualität beider Systeme gleich ist.

Durch eine Erhöhung der Leistungskenngröße  $ξ$  wird das  $\text{System C}$  im Gegensatz zum $\text{System A}$ nicht signifikant verbessert.  Ein solches Verhalten ist zum Beispiel bei Digitalsystemen feststellbar, bei denen das Sinken–SNR durch das Quantisierungsrauschen begrenzt wird.  Befindet man sich bereits auf dem horizontalen Abschnitt der Kurve, so ist durch eine größere Sendeleistung – und damit verbunden eine kleinere Bitfehlerwahrscheinlichkeit – kein besseres Sinken–SNR zu erzielen.

Meist werden die Größen  $ρ_v$  und  $ξ$  in logarithmierter Form dargestellt, wie in der rechten Grafik zu sehen ist:

• Durch die doppelt–logarithmische Darstellung ergibt sich für das  $\text{System A}$  weiterhin die Winkelhalbierende.  Die geringere Steigung  $($Faktor $3)$  von  $\text{System B}$  führt nun zu einer Verschiebung um  $10 · \lg 3 ≈ 5\text{ dB}$  nach unten.
• Der Schnittpunkt der Systeme  $\text{A}$  und  $\text{C}$  verschiebt sich durch die doppelt–logarithmische Darstellung von  $ξ = ρ_v = 10000$  auf  $10 · \lg ξ = 10 · \lg ρ_v = 40\text{ dB}$.

Aufgaben zum Kapitel

Aufgabe 1.2:   Verzerrungen? Oder keine Verzerrung?

Aufgabe 1.2Z:   Linear verzerrendes System

Aufgabe 1.3:   Systemvergleich beim AWGN–Kanal

Aufgabe 1.3Z:   Thermisches Rauschen