Contents
- 1 Differences between analog and digital modulation methods
- 2 ASK – Amplitude Shift Keying
- 3 Coherent demodulation of ASK signals
- 4 Inkohärente Demodulation von ASK–Signalen
- 5 BPSK – Binary Phase Shift Keying
- 6 Demodulation und Detektion von BPSK–Signalen
- 7 DPSK – Differential Phase Shift Keying
- 8 Differentiell-kohärente Demodulation des DPSK-Signals
- 9 Error probabilities - a brief overview
- 10 Aufgaben zum Kapitel
Differences between analog and digital modulation methods
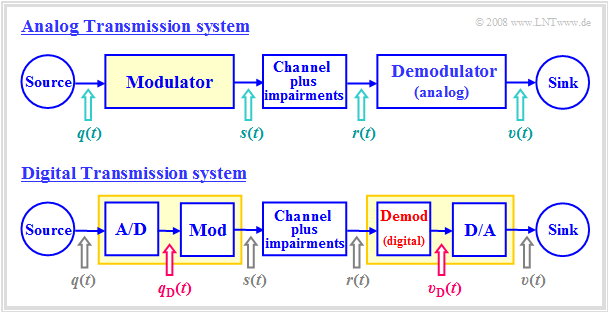
The diagram shows an analog transmission system at the top and a digital system drawn below. The main differences are highlighted in red:
- While in the upper system the analog source signal $q(t)$ is applied to the modulator input, in the lower digital system the modulating signal $q_{\rm D}(t)$ is a digital signal, characterized by the amplitude coefficients $a_ν$, the basic pulse $g_q(t)$ and the symbol duration $T$:
- $$q_{\rm D}(t) = \sum_{\nu=-\infty}^{+\infty}a_\nu \cdot g_q(t - \nu \cdot T) \hspace{0.05cm}.$$
- The A/D conversion can be done for example by pulse code modulation and includes the functions sampling, quantization, binary coding and signal shaping. The basic pulse $g_q(t)$ is often assumed to be NRZ-rectangular with amplitude $s_0$ and duration $T$. For the spectral function holds with ${\rm si}(x) = \sin(x)/x$:
- $$G_q(f) = s_0 · T · {\rm si}(π f T).$$
- The modulators can be the same for both systems. They change one of the three signal parameters of the carrier signal $z(t)$ according to the modulator input signal. The digital variants of AM, PM and FM are called Amplitude Shift Keying $\rm (ASK)$, Phase Shift Keying $\rm (PSK)$ and Frequency Shift Keying $\rm (FSK)$.
- In contrast, the demodulator of the digital system differs fundamentally from an analog demodulator by the required decision component (in hardware or software). Like $q_{\rm D}(t)$, the signal $v_{\rm D}(t)$ is digital and must then be D/A converted into the analog sink signal $v(t)$.
- The decisive quality criterion for both systems is the sink SNR ⇒ quotient of the power of the source signal $q(t)$ and the error signal $ε(t) = v(t) \ – \ q(t)$. In a digital system, one usually makes do with the quality characteristic Bit Error Rate $($ $\rm BER)$, which refers to the digital signals $q_{\rm D}(t)$ and $v_{\rm D}(t)$. This can be converted into a $\rm SNR$.
ASK – Amplitude Shift Keying
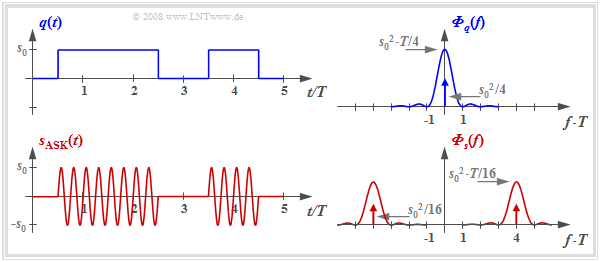
The diagram shows the digital source signal $q(t)$ – the index "D" is omitted from now on – and the ASK transmitted signal
- $$s_{\rm ASK}(t) = q(t) · \sin(2π · f_{\rm T} · t),$$
where unipolar amplitude coefficients $a_ν ∈ \{0, \ 1\}$ and a sinusoidal carrier are assumed here.
This method is used, for example, in optical transmission systems (since it is known that there are no negative light pulses) and is also known as "On–Off–Keying".
In the right half of the figure, the corresponding power-spectral densities $($abbreviated: $\rm PSD)$ are shown - although not to scale. With rectangular basic pulse $g_q(t)$ and equally probable unipolar amplitude coefficients holds:
- $$\begin{align*}{{\it \Phi}_{q}(f)}& = \frac{{s_0}^2 \cdot T}{4} \cdot {\rm si}^2 (\pi f T) + \frac{{s_0}^2 }{4} \cdot \delta (f)\hspace{0.05cm},\\ {{\it \Phi}_{s}(f)}& = \frac{1}{4} \cdot \big [ {{\it \Phi}_{q}(f- f_{\rm T})}+ {{\it \Phi}_{q}(f+ f_{\rm T})}\big]\hspace{0.05cm}.\end{align*}$$
It should be noted about these equations:
- The DC component $m_q = s_0/2$ of the source signal leads to a Dirac function at frequency $f = 0$ with weight ${s_0}^2/4$ in the power-spectral density $ϕ_q(f)$.
- The power-spectral density of the ASK transmitted signal is equal to $ϕ_s(f) = ϕ_q(f) ∗ ϕ_z(f)$, where the PSD $ϕ_z(f)$ of the carrier signal $z(t)$ is composed of two Dirac functions at $±f_{\rm T}$ with respective weight $1/4$. The equation is also valid with other carrier phase; the symbol "∗" describes the convolution.
- The power-spectral density $ϕ_s(f)$ is identical in shape to $ϕ_q(f)$ except for the shift by $±f_{\rm T}$ ⇒ the ASK belongs to the linear digital modulation methods.
Coherent demodulation of ASK signals
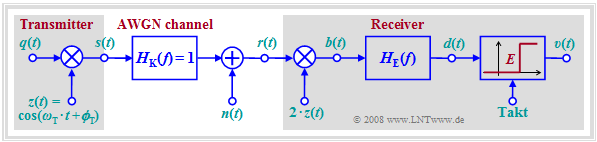
The diagram shows the block diagram of an ASK system including the receiver components.
- Let the source signal $q(t)$ be NRZ-rectangular and unipolar, that is, $a_ν ∈ \{0, \ 1\}$ .
- Let the channel be initially ideal, characterized by $H_{\rm K}(f) = 1$ and $n(t) = 0$ ⇒ $r(t) = s(t)$.
The demodulation is performed coherently by means of a synchronous demodulator, the operation of which has already been described for the analog modulation methods AM and PM.
To summarize:
- The same carrier signal is added at the receiver as at the transmitter, but with double amplitude. $z(t)$ denotes the carrier at the transmitter and the carrier at the receiver is $2 · z(t) = z_{\rm E}(t)$.
- Multiplication is followed by a suitably sized low-pass filter with frequency response $H_{\rm E}(f)$, which removes the higher frequency components of the signal $b(t)$.
- The detection signal $d(t)$ is sampled at instants $ν · T$ and decided using a threshold decision with threshold $E = {s_0}/2$.
- The sink signal $v(t)$ at the decision output is rectangular and in the noise-free case equal to the source signal $q(t)$ except for the transit time $T/2$.
$\text{To be noted:}$
- Coherent demodulation requires that the carrier frequency $f_{\rm T}$ and the carrier phase $ϕ_{\rm T}$ are exactly known to the receiver.
- The receiver must extract these two quantities from the received signal $r(t)$, which can be quite costly in the presence of strong channel distortion and large noise disturbances. Such realization aspects are dealt with, for example, in Exercise 4.9 to this chapter.
- If the carrier phase $ϕ_{\rm T}$ is not known to the receiver, this is called incoherent demodulation, even if the carrier frequency $f_{\rm T}$ is known.
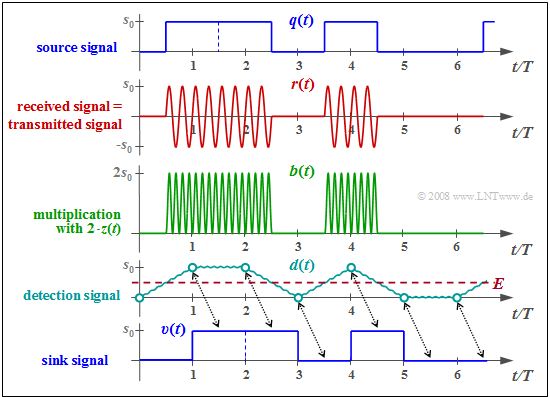
$\text{Example 1:}$ The diagram shows the signals mentioned in the ASK block diagram with ideal channel: $H_{\rm K}(f) = 1, \ \ n(t) = 0.$
The individual signal characteristics can be interpreted as follows:
- The transmitted signal $s(t)$ is the product of the unipolar source signal $q(t)$ and the carrier signal $z(t) = \sin(2π\hspace{0.05cm}f_{\rm T}\hspace{0.05cm}t)$, where in the example $f_{\rm T} = 4/T$ holds (only four oscillations per symbol duration).
- The received signal $r(t) = s(t)$ is first multiplied by the carrier $z_{\rm E}(t) = 2 · \sin(2π\hspace{0.05cm}f_{\rm T}\hspace{0.05cm}t)$ ⇒ twice the amplitude compared to $z(t)$, no frequency and phase offset. This gives:
- $$b(t) = 2 \cdot z(t)\cdot r(t)= 2 \cdot z^2(t)\cdot q(t) $$
- $$\Rightarrow \hspace{0.35cm}b(t) = q(t) \cdot \big [ 1 - \cos(4\pi\hspace{0.05cm} f_{\rm T}\hspace{0.05cm} t)\big] \hspace{0.05cm}.$$
- The low-pass filter with frequency response $H_{\rm E}(f) = {\rm si}(π\hspace{0.05cm} f_{\rm T}\hspace{0.05cm} T)$ and corresponding rectangular impulse response $h_{\rm E}(t)$ forms the detection signal $d(t) = b(t) \star h_{\rm E}(t)$ from the signal $b(t)$.
- $h_{\rm E}(t)$ is matched to the rectangular basic pulse $g_q(t)$; this is called the matched filter ⇒ best possible compromise between equalization and noise power limitation.
- In the absence of noise, $d(νT) = q(νT) ∈ \{0, \ s_0\}$. In the presence of (moderate) noise, it is very likely that $d(νT) > s_0/2,$ if $a_ν = +1$, and it will be $d(νT) < s_0/2$ for $a_ν = 0$.
- The decision obtains from the comparison of the detection samples $d(νT)$ with the threshold $E = s_0/2$ the sink signal $v(t)$, which is equal to $q(t)$ if the decision is error-free except for the running time $T/2$.
Inkohärente Demodulation von ASK–Signalen
Wir gehen weiter von ASK–Modulation sowie dem idealen, also
- verzerrungsfreien,
- dämpfungsfreien und
- rauschfreien
Übertragungskanal aus, so dass gilt:
- $$r(t) = s(t) = q(t) \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}.$$
Weiter wird für diesen Abschnitt vorausgesetzt, dass dem Empfänger zwar die Trägerfrequenz $f_{\rm T}$, nicht jedoch die Trägerphase $ϕ_{\rm T}$ bekannt ist. Üblich ist, auch diesen Demodulator als inkohärent zu bezeichnen.
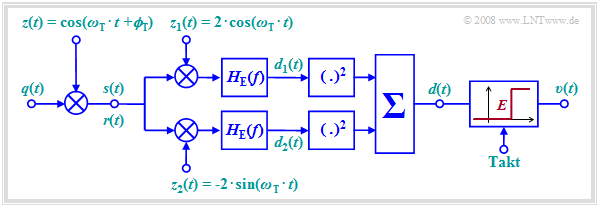
Die Grafik zeigt einen solchen inkohärenten Demodulator, dessen Funktionsweise hier nur stichpunktartig angegeben werden soll. Das Demodulationsergebnisse ist unabhängig von der Trägerphase $ϕ_{\rm T}$, die der Empfänger nicht kennt.
- Die Signale $d_1(t)$ und $d_2(t)$ nach den beiden Matched–Filtern mit jeweiligen Frequenzgang $H_{\rm E}(f)$ sind formgleich mit dem Detektionssignal $d(t)$ ⇒ $d_{\rm koh}(t)$ gemäß dem vorherigen Blockschaltbild , aber gegenüber diesem im Allgemeinen wegen der fehlenden Phasenanpassung gedämpft:
- $$d_1(t) = d_{\rm koh}(t) \cdot \cos( \phi_{\rm T}), \hspace{0.5cm}d_2(t) = -d_{\rm koh}(t) \cdot \sin( \phi_{\rm T}) \hspace{0.05cm}.$$
- Ist der Amplitudenkoeffizient $a_ν = 0$, so sind im rauschfreien Fall die beiden Signalwerte jeweils Null: $d_1(ν · T) = 0$ und $d_2(ν · T) = 0$. Andernfalls $(a_ν = 1)$ gilt für den Zeitpunkt $ν · T$:
- $$d_1(\nu \cdot T) = s_{\rm 0} \cdot \cos( \phi_{\rm T}), \hspace{0.5cm}d_2(\nu \cdot T) = -s_{\rm 0} \cdot \sin( \phi_{\rm T}) \hspace{0.05cm}.$$
- Nach Quadrierung der zwei Teilsignale erhält man für das Summensignal:
- $$d(\nu \cdot T) = \left\{ \begin{array}{c} 0 \\ {s_0}^2 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}a_\nu = 0, \\ {\rm falls}\hspace{0.15cm}a_\nu = 1. \\ \end{array}$$
- Durch die Schwellenwertentscheidung – sinnvollerweise mit der Entscheiderschwelle $E = {s_0}^2/2$ – können die Amplitudenkoeffizienten $a_ν$ entschieden werden. Allerdings ergibt sich eine etwas größere Bitfehlerwahrscheinlichkeit als bei kohärenter Demodulation.
BPSK – Binary Phase Shift Keying
Bei analoger Phasenmodulation $\rm (PM)$ lautet das Sendesignal:
- $$s_{\rm PM}(t) = s_0 \cdot \cos\big [2 \pi f_{\rm T} t + \phi_{\rm T}+ K_{\rm PM} \cdot q(t)\big ]\hspace{0.05cm}.$$
Bei bipolarem Quellensignal ⇒ $a_ν ∈ \{-1, +1\}$, der Trägerphase $ϕ_{\rm T} = π \ (180^\circ)$ und mit der Modulatorkonstanten $K_{\rm PM} = π/(2s_0)$ ergibt sich im $ν$–ten Zeitintervall:
- $$s_{\rm BPSK}(t) = \left\{ \begin{array}{c} s_0 \cdot \cos(2 \pi f_{\rm T} t + \pi+ \pi/2) \\ s_0 \cdot \cos(2 \pi f_{\rm T} t + \pi- \pi/2) \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}a_\nu = +1, \\ {\rm falls}\hspace{0.15cm}a_\nu = -1. \\ \end{array}$$
Diese Gleichung für die binäre Phasenmodulation $($englisch: Binary Phase Shift Keying, $\rm BPSK)$ lässt sich wie folgt umformen:
- $$s_{\rm BPSK}(t) = a_\nu \cdot s_0 \cdot \sin(2 \pi f_{\rm T} t ) $$
- $$\Rightarrow \hspace{0.3cm}s_{\rm BPSK}(t) = \left\{ \begin{array}{c} s_0 \cdot \sin(2 \pi f_{\rm T} t ) \\ -s_0 \cdot \sin(2 \pi f_{\rm T} t ) \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}a_\nu = +1, \\ {\rm falls}\hspace{0.15cm}a_\nu = -1. \\ \end{array}$$
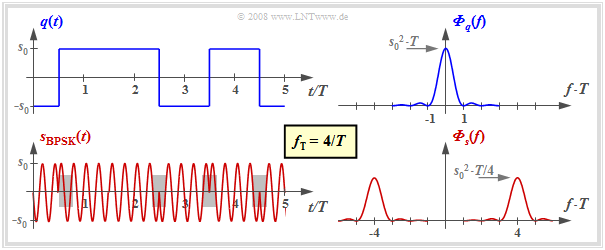
In der Grafik sind die Signale und die dazugehörigen Leistungsdichtespektren skizziert. Man erkennt:
- Das BPSK–Signal lässt sich wie das ASK–Signal als Produkt von Quellensignal $q(t)$ und Trägersignal $z(t)$ darstellen. Der einzige Unterschied liegt in den bipolaren Amplitudenkoeffizienten $a_ν ∈ \{-1, +1\}$ gegenüber den unipolaren Koeffizienten $(0$ oder $1)$ bei ASK.
- Im Gegensatz zur ASK ist bei der BPSK – wie bei jeder Form von Phasenmodulation – die Hüllkurve konstant. Die Information wird hier durch die Phasensprünge innerhalb des Sendesignals $s(t)$ übermittelt (graue Hinterlegungen in der Grafik).
- Die Leistungsdichtespektren bei BPSK unterscheiden sich von denen bei ASK lediglich durch die fehlenden Diracfunktionen $($da nun $q(t)$ keinen Gleichanteil beinhaltet$)$ sowie durch den Faktor $4$ bezüglich der kontinuierlichen LDS–Anteile.
- Daraus folgt weiter, dass die binäre Phasenmodulation zu den linearen Modulationsverfahren gezählt werden kann. Im Allgemeinen ist nämlich die (analoge) Phasenmodulation bis auf wenige Ausnahmen hinsichtlich des Quellensignals nichtlinear.
- Für die Grafiken wurden aus Darstellungsgründen im Abschnitt ASK (Sinus) und und hier bei BPSK (Minus–Cosinus) verschiedene Trägerphasen gewählt. Diese willkürliche Festlegung ist jedoch keine Einschränkung. Beide Verfahren funktionieren bei anderen Trägerphasen in gleicher Weise.
Demodulation und Detektion von BPSK–Signalen
Aufgrund der konstanten Hüllkurve des BPSK–Signals muss hier die Demodulation stets kohärent erfolgen. Es kann dabei vom gleichen Blockschaltbild wie bei der kohärenten ASK–Demodulation ausgegangen werden.
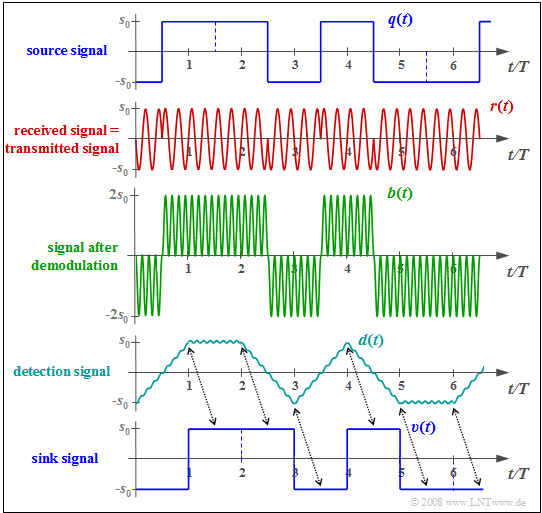
$\text{Beispiel 2:}$ Die Grafik zeigt von oben nach unten
- das Quellensignal $q(t)$,
- das Empfangssignal $r(t) = s(t)$ bei idealem Kanal,
- das Signal $b(t)$ nach Multiplikation mit dem empfängerseitigen Trägersignal $z_{\rm E}(t) = 2 \cdot z(t)$,
- das Detektionssignal $d(t)$ nach "Integration" durch das Matched-Filter,
- das Sinkensignal $v(t)$.
Ein Vergleich mit den entsprechenden Signalen bei der kohärenten Demodulation der ASK zeigt:
- Die Rechtecksignale $q(t)$ und $v(t)$ sind nun bipolar.
- Für das Detektionssignal bei BPSK gilt im Vergleich zur ASK:
- $$d_{\rm BPSK}(t) = 2 \cdot d_{\rm ASK}(t)-s_0.$$
- Im betrachteten dämpfungs–, verzerrungs– und rauschfreien Fall sind alle Detektionsabtastwerte $d(ν · T) = ±s_0$. Deshalb sollte hier die Entscheiderschwelle $E = 0$ verwendet werden.
- Man erkennt den doppelten Abstand der BPSK–Detektionsabtastwerte (Kreismarkierungen) von der Schwelle, was die Fehlerwahrscheinlichkeit entscheidend verbessert.
DPSK – Differential Phase Shift Keying
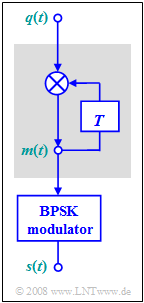
Die nebenstehende Grafik zeigt das Blockschaltbild des Modulators für Differential Phase Shift Keying $\rm (DPSK)$.
- Das (bipolare) Quellensignal $q(t)$ mit den Amplitudenkoeffizienten $q_ν ∈ \{-1, +1\}$ wird entsprechend dieses Mappings in das Signal $m(t)$ mit den Amplitudenkoeffizienten
- $$m_{\nu} = m_{\nu -1} \cdot q_{\nu} \in \{ -1, +1\}$$
abgebildet, bevor es dem BPSK–Modulator zugeführt wird.
- Ist $q_ν = m_{ν-1},$ so ergibt sich der gemappte Amplitudenkoeffizient $m_ν = +1$.
- Dagegen weist $m_ν = -1$ darauf hin, dass sich die Amplitudenkoeffizienten $q_ν$ und $m_{ν-1}$ unterscheiden.
Wesentlicher Vorteil der differentiellen binären Phasenmodulation ist, dass das so entstehende Signal $s(t)$ auch ohne Kenntnis der Trägerphase $ϕ_{\rm T}$ demoduliert werden kann, siehe nächster Abschnitt.
Obwohl dem Empfänger die genaue Trägerfrequenz $f_{\rm T}$ bekannt sein muss, spricht man trotzdem von einem inkohärenten, manchmal auch vom differentiell–kohärenten PSK–Demodulator.
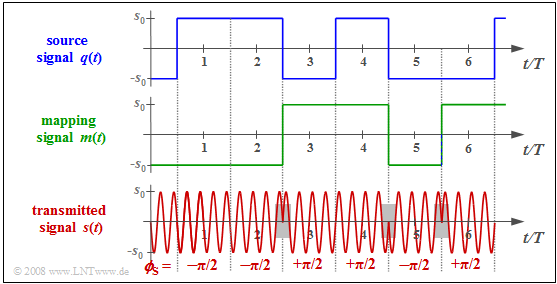
$\text{Beispiel 3:}$ Die rechts dargestellte Grafik zeigt
- das Quellensignal $q(t)$
- das Mapping–Signal $m(t)$ sowie
- das DPSK–Sendesignal $s(t)$.
Im Folgenden bezeichnet $v_ν$ die Koeffizienten nach der Entscheidung, die mit den sendeseitigen Amplitudenkoeffizienten $q_ν$ übereinstimmen sollten. Man erkennt folgendes Prinzip:
- Immer dann, wenn der Empfänger einen Phasensprung erkennt, entscheidet er sich für sich $v_ν = -1$. Es gilt:
- $$v_3 = v_5 =v_6 =-1.$$
- Ist kein Phasensprung erkennbar ist, so wird $v_ν = +1$ gesetzt:
- $$v_1 = v_2 =v_4 =+1.$$
Unterhalb des Sendesignals sind für die ersten sechs Symbole die Phasenwerte $ϕ_{\rm S}$ angegeben.
- Durch eine zusätzliche Phasendrehung auf dem Kanal, zum Beispiel um $70.3π$, ändern sich zwar die absoluten Phasenwerte auf $69.8π$, $69.8π$, $70.8π$, $70.8π$, $69.8π$ und $70.8π$.
- Die Phasendifferenz benachbarter Symbole bleibt jedoch erhalten, so dass die differentiell–kohärente Demodulation trotzdem funktioniert. Ein entsprechender Demodulator wird im folgenden Abschnitt vorgestellt.
Differentiell-kohärente Demodulation des DPSK-Signals
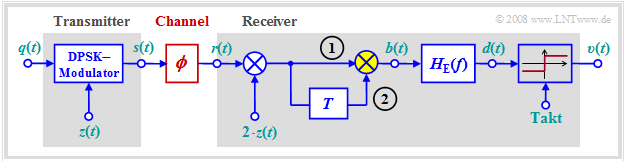
Dargestellt ist das Blockschaltbild eines Übertragungssystems mit DPSK–Modulation (Differential Phase Shift Keying) und differentiell–kohärenter Demodulation.
Stichpunktartig lässt sich die Funktionsweise wie folgt beschreiben:
- Ohne Berücksichtigung der Modulation mit den Trägersignalen $z(t)$ bzw. $2 · z(t)$ liegt im Intervall $ν$ am Eingang (1) des gelb hervorgehobenen Multiplizierers das Symbol $m_ν = m_{ν-1} · q_ν$ an und am Eingang (2) das Symbol $m_{ν-1}$.
- Die Multiplikation von (1) und (2) ergibt das gewünschte Ergebnis, nämlich $v_ν = m_{ν-1} · q_ν · m_{ν-1} = q_ν$. Berücksichtigt ist hierbei, dass $m_{ν-1} ∈ \{+1, –1\}$ gilt.
- Das Matched–Filter mit dem Frequenzgang $H_{\rm E}(f)$ eliminiert die unerwünschten Anteile um die doppelte Trägerfrequenz, die durch die zweifache Multiplikation mit $z(t)$ bzw. $2 · z(t)$ entstehen. Bei rechteckförmigem Grundimpuls $g_q(t)$ lässt sich der Frequenzgang $H_{\rm E}(f)$ auch sehr einfach durch einen Integrator realisieren.
- Wir nehmen an, dass der Kanal eine Phasendrehung um $ϕ$ bewirkt, die der Empfänger nicht kennt (roter Block). Geht man beispielsweise vom sendeseitigen Träger $z(t) = \cos (2π · f_{\rm T} · t)$ aus, so beinhaltet das Empfangssignal $r(t)$ einen multiplikativen Anteil mit $\cos (2π · f_{\rm T} · t + ϕ)$. Die Zusetzung des empfangsseitigen Trägers $2 · z(t)$ erfolgt also nicht phasensynchron.
- Das um eine Symboldauer $T$ verzögerte Signal $r(t – T)$ weist die gleiche Phase $ϕ$ auf. Durch die Korrelation zwischen $2 · r(t) · z(t)$ und $2 · r(t – T) · z(t – T)$ wird erreicht, dass das Entscheiderergebnis unabhängig von der zufälligen Phase $ϕ$ ist. Man bezeichnet diese Art der Demodulation als differentiell–kohärent.
Error probabilities - a brief overview
Die Fehlerwahrscheinlichkeiten der behandelten digitalen Modulationsverfahren (ASK, BPSK, DPSK) werden in Kapitel Lineare digitale Modulation – Kohärente Demodulation des Buches „Digitalsignalübertragung” unter verschiedenen Randbedingungen berechnet.
Hier werden nur einige Ergebnisse ohne Beweis vorweg genommen, gültig für
- ein Sendesignal mit der mittleren Energie $E_{\rm B}$ pro Bit,
- AWGN–Rauschen mit der (einseitigen) Rauschleistungsdichte $N_0$, und
- bestmögliche Empfänger–Realisierung nach dem Matched-Filter-Prinzip.
Betrachten wir zunächst die Bitfehlerwahrscheinlichkeit von Binary Phase Shift Keying $\rm (BPSK)$ unter der Voraussetzung eines kohärenten Empfängers:
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{ {2 \cdot E_{\rm B} }/{N_0 } } \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{ {E_{\rm B} }/{N_0 } } \hspace{0.1cm}\right ).$$
Dagegen git für Amplitude Shift Keying $\rm (ASK)$ bei kohärenter Demodulation:
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{{E_{\rm B} }/{N_0 } } \hspace{0.1cm}\right ) ={1}/{2}\cdot {\rm erfc}\left ( \sqrt{ {E_{\rm B}}/{(2 \cdot N_0) } } \hspace{0.1cm}\right ).$$
In den Formeln wurden zwei Varianten der komplementären Gaußschen Fehlerfunktion verwendet:
- $${\rm Q} ({\it x}) = \frac{\rm 1}{\sqrt{\rm 2\pi} }\int_{\it x}^{+\infty}{\rm e}^{ {\it -u}^{\rm 2}/\rm 2}\,{\rm d} {\it u} \hspace{0.05cm},\hspace{0.3cm} {\rm erfc} ( {\it x} ) = \frac{\rm 2}{\sqrt{\rm \pi} }\int_{\it x}^{+\infty}{\rm e}^{ {\it -u}^{\rm 2} }\,{\rm d} {\it u} \hspace{0.05cm}.$$
Trägt man die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ über den Quotienten $E_{\rm B}/N_0$ in doppelt–logarithmischem Maßstab auf, so liegt die ASK–Kurve stets um $3 \ \rm dB$ rechts von der BPSK–Kurve. Diese Degradation ist auch ein Grund dafür, dass ASK in der Praxis nur selten eingesetzt wird.
Der entscheidende Vorteil von Differential Phase Shift Keying (DPSK) ist es, dass diese auch ohne Kenntnis der Trägerphase demoduliert werden kann. Diese einfache Realisierung erkauft man sich durch eine gegenüber der kohärenten BPSK erhöhten Fehlerwahrscheinlichkeit:
- $$p_{\rm B} = {1}/{2}\cdot {\rm e}^{ - {E_{\rm B} }/{N_0 } } .$$
Die inkohärente Demodulation eines BPSK–Signals ist dagegen nicht möglich. Für die inkohärente ASK–Demodulation erhält man:
- $$p_{\rm B} = {1}/{2}\cdot {\rm e}^{-{E_{\rm B}}/{(2N_0) }} .$$
- Beispielsweise benötigt man bei der BPSK $10 · \lg \ E_{\rm B}/N_0 ≈ 8.4 \ \rm dB$, um die Fehlerwahrscheinlichkeit $p_{\rm B} = \rm 10^{–4}$ zu erreichen. Allerdings ist hierzu stets eine kohärente Demodulation erforderlich.
- Bei der (differentiell–kohärenten) DPSK sind hierfür $9.3 \ \rm dB$ notwendig, also fast ein Dezibel mehr, und bei der ASK sogar $11.4 \ \rm dB$ (bei kohärenter Demodulation) bzw. $12.3 \ \rm dB$ (bei inkohärenter Demodulation).
Die hier angegebenen Gleichungen sollen in der Aufgabe 4.8 ausgewertet werden.
Aufgaben zum Kapitel
Aufgabe 4.7: Spektren von ASK und BPSK
Aufgabe 4.7Z: Signalformen bei ASK, BPSK und DPSK
Aufgabe 4.8: Fehlerwahrscheinlichkeiten
Aufgabe 4.8Z: BPSK–Fehlerwahrscheinlichkeit
Aufgabe 4.9: Costas–Regelschleife