Equivalent Low-Pass Signal and its Spectral Function
Contents
- 1 Motivation für die Beschreibung im äquivalenten Tiefpassbereich
- 2 Definition im Frequenzbereich
- 3 Beschreibung im Zeitbereich
- 4 Definition der Ortskurve
- 5 Darstellung nach Betrag und Phase
- 6 Zusammenhang zwischen äquivalentem TP-Signal und BP-Signal
- 7 Warum gibt es für das gleiche Signal drei Darstellungsformen?
- 8 Darstellung nach Real- und Imaginärteil
- 9 Ermittlung des äquivalenten TP-Signals aus dem BP-Signal
- 10 Leistung und Energie eines Bandpass-Signals
- 11 Aufgaben zum Kapitel
Motivation für die Beschreibung im äquivalenten Tiefpassbereich
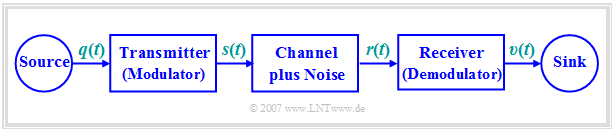
Die folgende Grafik zeigt einen möglichen Aufbau eines Nachrichtenübertragungssystems:
- Häufig wird das niederfrequente Quellensignal $q(t)$ in ein Bandpass–Signal $s(t)$ umgesetzt ⇒ Modulation.
- Nach der Übertragung muss das Empfangssignal $r(t)$ – gegenüber dem Sendesignal $s(t)$ eventuell verzerrt und mit (Rausch-)Störungen beaufschlagt – wieder in den ursprünglichen Frequenzbereich zurückgesetzt werden ⇒ Demodulation.
- Das Sinkensignal $v(t)$, das möglichst gut mit dem Quellensignal $q(t)$ übereinstimmen sollte, ist dann wieder ein Tiefpass–Signal.
Modulation und Demodulation sind also fundamentale Komponenten eines Übertragungssystems, die im Buch Modulation Methods eingehend behandelt werden. Eine kurze Zusammenfassung finden Sie im ersten Kapitel Prinzip der Nachrichtenübertragung des vorliegenden Buches.
Die Untersuchung, Simulation, Optimierung und Dimensionierung von Bandpass-Systemen erfolgen meist im äquivalenten Tiefpassbereich, wofür folgende Gründe genannt werden können:
- Sind Qualitätsmerkmale (Bandbreiteneffizienz, Signal-zu-Rauschverhältnis, Bitfehlerrate, Leistungsbedarf, usw.) eines Tiefpass-Systems bekannt, so lassen sich die entsprechenden Werte verwandter Bandpass-Systeme daraus relativ einfach herleiten. Beispiele hierfür sind die digitalen Modulationsverfahren Amplitude Shift Keying (ASK) und Binary Phase Shift Keying (BPSK), deren Performance-Größen aus dem vergleichbaren Basisbandsystem (also ohne Modulator und Demodulator) „hochgerechnet” werden können.
- Einzelne Teilkanäle bei einem so genannten Frequenzmultiplexsystem, die sich durch verschiedene Trägerfrequenzen unterscheiden, können oft als qualitativ gleichwertig angesehen werden. Deshalb genügt es, die Berechnung und Dimensionierung auf einen einzigen Kanal zu beschränken und diese Untersuchungen im äquivalenten Tiefpass-Bereich – das heißt ohne Berücksichtigung der spezifischen Trägerfrequenz – durchzuführen.
- Häufig ist es so, dass die Bandbreite einer Nachrichtenverbindung um Größenordnungen kleiner ist als die Trägerfrequenz. So liegen beispielsweise beim GSM-Mobilfunk die einzelnen Kanäle im Frequenzbereich um $900\ \rm MHz$ („D-Netz”) bzw. $1800\ \rm MHz$ („E-Netz”), während jedem Kanal nur eine geringe Bandbreite von $200\ \rm kHz$ zur Verfügung steht. Deshalb ist eine Simulation im äquivalenten Tiefpass–Bereich sehr viel weniger aufwändig als eine Simulation der entsprechenden Bandpass–Signale.
Definition im Frequenzbereich
Wir betrachten ein reelles Bandpass–Signal $x(t)$ mit dem Spektrum $X(f)$. Weiterhin soll gelten:
- Das Bandpass–Signal $x(t)$ sei aus der Modulation eines niederfrequenten Nachrichtensignals $q(t)$ mit dem Trägersignal $z(t)$ der Frequenz $f_{\rm T}$ entstanden. Die Art der Modulation (ob analog oder digital, Amplituden– oder Winkelmodulation, Einseitenband oder Zweiseitenband) sei nicht festgelegt.
- Die Spektralfunktion $X_+(f)$ des dazugehörigen analytischen Signals $x_+(t)$ existiert nur für positive Frequenzen und ist hier doppelt so groß wie $X(f)$. Für die Herleitung von $X_+(f)$ muss die Trägerfrequenz $f_{\rm T}$ des Systems nicht bekannt sein.
$\text{Definition:}$ Verschiebt man das Spektrum des analytischen Signals $x_+(t)$ um $f_{\rm T}$ nach links, so bezeichnet man das Ergebnis als das Spektrum des äquivalenten Tiefpass-Signals:
- $$X_{\rm TP}(f) = X_{\rm +}(f + f_{\rm T}).$$
Im allgemeinen sind $X(f)$, $X_+(f)$ und $X_{\rm TP}(f)$ komplexwertig. Ist allerdings $X(f)$ rein reell, so sind auch die Spektralfunktionen $X_+(f)$ und $X_{\rm TP}(f)$ rein reell, weil sich diese aus $X(f)$ nur aus den Operationen „Abschneiden und Verdoppeln” bzw. „Frequenzverschiebung” ergeben.
Bei der Berechnung des äquivalenten Tiefpass–Spektrums $X_{\rm TP}(f)$ ist – im Gegensatz zu $X_+(f)$ – die Kenntnis der Trägerfrequenz $f_{\rm T}$ unbedingt erforderlich. Für andere Werte von $f_{\rm T}$ ergeben sich auch andere Tiefpass–Spektren.
Transformiert man obige Gleichung in den Zeitbereich, so erhält man nach Anwendung des Verschiebungssatzes:
- $$x_{\rm TP}(t) = x_{\rm +}(t)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}.$$
Mit der Beziehung $x(t) = \text{Re}\big[x_+(t)\big]$ ergibt sich die Vorgehensweise, wie aus dem äquivalenten Tiefpass–Signal das tatsächliche, physikalische Bandpass–Signal ermittelt werden kann:
- $$x(t) = {\rm Re}[x_{\rm +}(t)] = {\rm Re}\big[x_{\rm TP}(t)\cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot 2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_{\rm T}\hspace{0.05cm} \cdot \hspace{0.05cm} \hspace{0.05cm}t}\big].$$
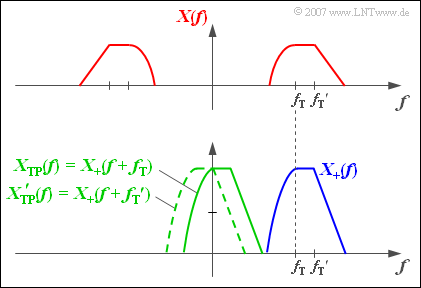
$\text{Beispiel 1:}$ Die obere Grafik zeigt die rein reelle Spektralfunktion $X(f)$ eines Bandpass–Signals $x(t)$, das aus der Modulation eines niederfrequenten Signals $q(t)$ mit der Trägerfrequenz $f_{\rm T}$ entstanden sei.
Darunter dargestellt sind die beiden ebenfalls reellen Spektralfunktionen $X_+(f)$ und $X_{\rm TP}(f)$. Aufgrund der Unsymmetrien bezüglich des Frequenzursprungs $(f = 0)$ sind die zugehörigen Zeitfunktionen komplex.
- Die durchgezogen–grün dargestellte Spektralfunktion $X_{\rm TP}(f)$ ist gegenüber $X_{+}(f)$ um die Trägerfrequenz $f_{\rm T}$ nach links verschoben.
- Wäre das Spektrum $X(f)$ aber das Modulationsergebnis eines anderen Nachrichtensignals $q\hspace{0.05cm}'(t)$ mit anderer Trägerfrequenz ${f_{\rm T} }\hspace{0.05cm}'$, so ergäbe sich auch ein anderes äquivalentes TP–Signal ${X_{\rm TP} }\hspace{0.05cm}'(f)$.
- Eine beispielhafte Spektralfunktion ${X_{\rm TP} }\hspace{0.05cm}'(f)$ ist in der Grafik grün-gestrichelt eingezeichnet.
Beschreibung im Zeitbereich
Zur Vereinfachung der Darstellung gehen wir nun von einem Linienspektrum aus, so dass man das analytische Signal als Zeigerverbund ⇒ Summe von komplexen Drehzeigern darstellen kann:
- $$X_{+}(f) = \sum_{i=1}^{I} {A_i} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_i}\cdot\delta (f - f_i) \hspace{0.3cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} x_{+}(t) = \sum_{i=1}^{I} A_i \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}( 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_i\hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$
Durch die Frequenzverschiebung um $f_{\rm T}$ nach links lautet somit das äquivalente Tiefpass–Signal in Frequenz– und Zeitbereich:
- $$X_{\rm TP}(f) = \sum_{i=1}^{I} {A_i} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_i}\cdot\delta (f - \nu_i)\hspace{0.3cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} x_{\rm TP}(t) = \sum_{i=1}^{I} A_i \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}( 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu_i \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$
Zwischen den Frequenzwerten $f_i$ und $\nu_i$ gilt folgender Zusammenhang $(i = 1, \ \text{...} \ , I)$:
- $$\nu_i = f_i - f_{\rm T} .$$
Diese Gleichungen können wie folgt interpretiert werden:
- Zur Zeit $t = 0$ ist das äquivalente Tiefpass-Signal identisch mit dem analytischen Signal:
- $$x_{\rm TP}(t = 0) = x_{\rm +}(t = 0)= \sum_{i=1}^{I} A_i \cdot {\rm e}^{{-\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_i}.$$
- Zu diesem Zeitpunkt ist der Zeigerverbund demnach allein durch die $I$ Amplitudenparameter $A_i$ und die $I$ Phasenlagen $\varphi_i$ festgelegt.
- Alle Zeiger des analytischen Signals $x_+(t)$ drehen für $t > 0$ entsprechend den (stets positiven) Frequenzen $f_i$ entgegen dem Uhrzeigersinn.
- Beim äquivalenten Tiefpass-Signal sind die Drehgeschwindigkeiten geringer. Zeiger mit $\nu_i > 0$ drehen in mathematisch positiver Richtung (entgegen dem Uhrzeigersinn), solche mit $\nu_i < 0$ in Gegenrichtung (im Uhrzeigersinn).
- Ist bei einem Zeiger der Frequenzparameter $\nu_i =0$, so ruht dieser Zeiger in der komplexen Ebene entsprechend seiner Ausgangslage.
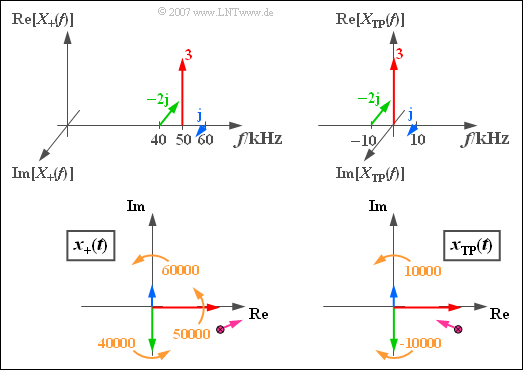
$\text{Beispiel 2:}$ Wir betrachten ein aus drei Spektrallinien bei $40\,\text{kHz}$, $50\,\text{kHz}$ und $60\,\text{kHz}$ bestehendes Spektrum $X_+(f)$. Mit den aus der Grafik erkennbaren Amplituden– und Phasenparametern erhält man das analytische Signal $x_+(t)$ entsprechend der unteren linken Skizze.
Die Momentaufnahme der linken unteren Grafik ⇒ analytisches Signal $x_+(t)$ gilt für die Zeit $t = 0$. Alle Zeiger drehen danach mit jeweils konstanter Winkelgeschwindigkeit entgegen dem Uhrzeigersinn.
- Der blaue Zeiger dreht hierbei mit $60000$ Umdrehungen pro Sekunde am schnellsten und der grüne Zeiger mit der Kreisfrequenz $\omega_{40} = 2\pi \cdot 40000 \hspace{0.1cm} 1/\text{s}$ am langsamsten.
- Der violette Summenpunkt aller drei Zeiger bewegt sich für $t > 0$ in der komplexen Ebene in komplizierter Weise, bei obigen Zahlenwerten zuerst grob in die eingezeichnete Richtung.
Die rechten Grafiken beschreiben das äquivalente Tiefpass–Signal im Frequenzbereich (oben) und im Zeitbereich (unten), gültig für $f_{\rm T} = 50\,\text{kHz}$.
- Der Träger liegt nun bei $f = 0$ und der dazugehörige rote Drehzeiger bewegt sich nicht.
- Der blaue Zeiger (OSB) dreht hier mit $\omega_{10} = 2\pi \cdot 10000 \hspace{0.1cm}1/\text{s}$ entgegen dem Uhrzeigersinn.
- Der grüne Zeiger (USB) dreht mit gleicher Geschwindigkeit entgegengesetzt ($-\omega_{10}$).
Definition der Ortskurve
$\text{Definition:}$ Als Ortskurve bezeichnen wir den Kurvenzug, auf dem sich das äquivalente Tiefpass-Signal $x_{\rm TP}(t)$ in der komplexen Ebene bewegt.
Hinweis: In anderer Fachliteratur wird dieser Begriff eher selten verwendet. Deshalb zunächst ein Beispiel.
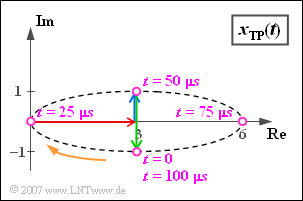
$\text{Beispiel 3:}$ Wir betrachten das äquivalente Tiefpass–Signal $x_{\rm TP}(t)$ von $\text{Beispiel 2}$, bestehend aus
- dem ruhenden Zeiger der Länge $3$ (rot)
- dem mit $\omega_{10} = 2\pi \cdot 10000 \hspace{0.1cm} 1/\text{s}$ in mathematisch positiver Richtung rotierenden blauen Zeiger mit der komplexen Amplitude j,
- den grünen Zeiger der Länge $2$, der zur Zeit $t = 0$ in Richtung der negativen imaginären Achse liegt. Dieser dreht mit gleicher Winkelgeschwindigkeit $\omega_{10}$ wie der blaue Zeiger, aber in umgekehrter Richtung ($-\omega_{10}$).
Der blaue Zeiger und der grüne Zeiger benötigen für eine Umdrehung jeweils genau eine Periodendauer $T_0 = 100 \,{\rm µ}\text{s}$. Der weitere Verlauf kann obiger Darstellung entnommen werden:
- Die violett eingezeichnete Zeigersumme ist zum Zeitpunkt $t = 0$ gleich $3 - \text{j}$.
- Nach $t = T_0/4 = 25 \,{\rm µ}\text{s}$ hat der resultierende Zeigerverbund den Wert „Null”, da nun die beiden rotierenden Zeiger in Gegenrichtung zum Träger liegen und diesen exakt kompensieren.
- Nach einer Periodendauer $(t = T_0 = 100 \,{\rm µ}\text{s})$ ist wieder der Ausgangszustand erreicht: $x_{\rm TP}(t = T_0) = x_{\rm TP}(t=0) = 3 - \text{j}$.
In diesem Beispiel ist die Ortskurve eine Ellipse, die vom äquivalenten Tiefpass–Signal pro Periodendauer einmal durchlaufen wird.
- Die Darstellung gilt für die Zweiseitenband–Amplitudenmodulation mit Träger eines sinusförmigen $10\ \rm kHz$–Signals mit einem cosinusförmigen Träger beliebiger Frequenz, wobei das obere Seitenband (blauer Zeiger) gedämpft ist.
- Wären die Längen des blauen und des grünen Drehzeigers gleich, so ergäbe sich als Ortskurve eine Horizontale auf der reellen Achse – siehe Aufgabe 4.5.
- Im Buch Modulationsverfahren werden die Ortskurven verschiedener Systemvarianten noch eingehend behandelt.
Darstellung nach Betrag und Phase
Das äquivalente Tiefpass-Signal des Bandpass-Signals $x(t)$ ist im allgemeinen komplex und kann deshalb auch in der Form
- $$x_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t)}$$
dargestellt werden. Zu beachten ist das Pluszeichen im Argument der Exponentialfunktion, das sich von der komplexen Fourierreihendarstellung unterscheidet. Man verwendet nämlich bei der Beschreibung der Modulationsverfahren auch für das physikalische Signal meist die Gleichung mit dem positiven Vorzeichen für die Phase:
- $$x(t) = a(t) \cdot {\cos} ( 2 \pi f_{\rm T} t + \phi(t)).$$
In vielen Lehrbüchern wird diese Gleichung je nach Anwendung mit Plus– oder Minuszeichen benutzt, aber stets mit gleichem „Phasenbezeichner”. Durch die Verwendung zweier verschiedener Symbole $(\varphi$ und $\phi)$ versuchen wir in unserem Lerntutorial $\rm LNTwww$, diese Doppeldeutigkeit zu umgehen.
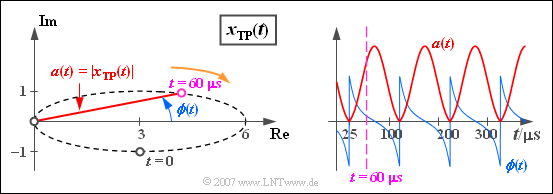
$\text{Beispiel 4:}$ Es gelten die gleichen Voraussetzungen wie im $\text{Beispiel 2}$ und im $\text{Beispiel 3}$. In der Grafik sind aber nun statt der komplexen Funktion $x_{\rm TP}(t)$ die beiden reellen Funktionen $a(t)$ und $\phi(t)$ dargestellt.
Zu dieser Darstellung ist anzumerken:
- Die Betragsfunktion gibt die Zeitabhängigkeit der Zeigerlänge wieder:
- $$a(t)= \vert x_{\rm TP}(t)\vert =\sqrt{ {\rm Re}\left[x_{\rm TP}(t)\right]^2 + {\rm Im}\left[x_{\rm TP}(t)\right]^2 }.$$
- Die Betragsfunktion $a(t)$ ist in diesem Beispiel wie das komplexe äquivalente Tiefpass-Signal $x_{\rm TP}(t)$ periodisch mit $T_0$ und nimmt Werte zwischen $0$ und $6$ an.
- Die Phasenfunktion beschreibt den zeitabhängigen Winkel des äquivalenten Tiefpass-Signals $x_{\rm TP}(t)$, bezogen auf den Koordinatenursprung:
- $$\phi(t)= {\rm arc} \left[x_{\rm TP}(t)\right]= {\rm arctan} \hspace{0.1cm}\frac{ {\rm Im}\left[x_{\rm TP}(t)\right]}{ {\rm Re}\left[x_{\rm TP}(t)\right]}.$$
Hier noch einige numerische Ergebnisse für die Phasenwerte:
- Die Phase im Startzeitpunkt ist $\phi (t = 0) =\hspace{0.1cm} -\arctan (1/3) ≈ \hspace{0.1cm} -18.43^{\circ} = \hspace{0.1cm}-0.32\,\text{rad}$.
- Bei $t = 25\,{\rm µ}\text{s}$ sowie zu allen äquidistanten Zeiten davon im Abstand $T_0 = 100 \,{\rm µ}\text{s}$ ist $x_{\rm TP}(t) = 0$, so dass zu diesen Zeitpunkten die Phase $\phi(t)$ sprungartig von $-\pi /2$ auf $+\pi /2$ wechselt.
- Zum violett eingezeichneten Zeitpunkt $t = 60\,{\rm µ}\text{s}$ hat die Phase einen leicht positiven Wert.
Zusammenhang zwischen äquivalentem TP-Signal und BP-Signal
Ein bandpassartiges Signal $x(t)$, das sich aus der Modulation eines niederfrequenten Nachrichtensignals $q(t)$ mit einem Trägersignal $z(t)$ der Frequenz $f_{\rm T}$ ergeben hat, kann wie folgt dargestellt werden:
- $$x(t) = a(t) \cdot {\cos} ( 2 \pi f_{\rm T} t + \phi(t)) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} x_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t)}.$$
Hierzu ist anzumerken:
- $a(t)$ ist die zeitabhängige Amplitude, die man oft auch als Hüllkurve bezeichnet. Diese ist gleich dem Betrag $|x_{\rm TP}(t)|$ des äquivalenten Tiefpass–Signals.
- $\phi(t)$ ist die Phasenfunktion, also die zeitabhängige Phase, die ebenfalls aus dem äquivalenten Tiefpass–Signal als der Winkel zum Koordinatenursprung der komplexen Ebene ermittelt werden kann.
- Im physikalischen Signal $x(t)$ erkennt man die Phase $\phi(t)$ an den Nulldurchgängen. Bei $\phi(t) > 0$ tritt der Nulldurchgang in $x(t)$ im Bereich der Zeit $t$ früher auf als beim Trägersignal $z(t)$. Dagegen bedeutet $\phi(t) < 0$ eine Verschiebung des Nulldurchgangs auf einen späteren Zeitpunkt.
- Man spricht von Amplitudenmodulation, wenn die gesamte Information über das Nachrichtensignal in der Hüllkurve $a(t)$ steckt, während $\phi(t)$ konstant ist.
- Dagegen beinhaltet bei Phasenmodulation die Phasenfunktion $\phi(t)$ die gesamte Information über das Nachrichtensignal, während $a(t)$ konstant ist.
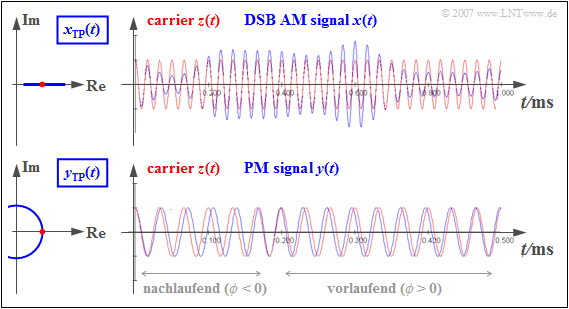
$\text{Beispiel 5:}$ Der obere Teil der folgenden Grafik beschreibt die Zweiseitenband–Amplitudenmodulation (ZSB-AM) mit Träger:
- Das äquivalente TP–Signal $x_{\rm TP}(t)$ ist hier stets reell ⇒ die Ortskurve ist eine horizontale Gerade.
- Deshalb stimmen die Nulldurchgänge des blauen ZSB–AM–Signals $x(t)$ mit denen des roten Trägersignals $z(t)$ exakt überein.
- Das heißt: Die Phasenfunktion $\phi(t)$ ist identisch Null ⇒ die Hüllkurve $a(t)$ beinhaltet die gesamte Information über das Nachrichtensignal.
Der untere Grafikteil gilt dagegen für die Phasenmodulation (PM):
- Das PM-Signal $y(t)$ hat stets eine konstante Einhüllende ⇒ die Ortskurve ist ein Kreisbogen.
- Der Phasenwert ist hier zunächst kleiner Null ⇒ die $y(t)$–Nulldurchgänge treten später auf als die des Trägers $z(t)$ ⇒ die Nulldurchgänge sind „nachlaufend”.
- Bei positiven Werten des Nachrichtensignals gilt auch $\phi (t) > 0$ ⇒ die Nulldurchgänge treten früher auf als beim Trägersignal ⇒ sie sind „vorlaufend”.
- Bei Phasenmodulation steckt also die gesamte Information über das Nachrichtensignal $q(t)$ in den Lagen der Nulldurchgänge.
Warum gibt es für das gleiche Signal drei Darstellungsformen?
Abschließend – hoffentlich nicht zu spät – wollen wir uns noch der Frage zuwenden, warum die beiden komplexen und im Verständnis komplizierteren Signale $x_+(t)$ und $x_{\rm TP}(t)$ zur Beschreibung des tatsächlichen Bandpass–Signals $x(t)$ eigentlich notwendig sind. Sie wurden nicht deshalb in der Nachrichtentechnik eingeführt, um Studierende zu verunsichern, sondern:
$\text{Fazit:}$
- Die Hüllkurve $a(t)$ und die Phasenfunktion $\phi (t)$ können aus dem tatsächlichen, physikalischen BP–Signal $x(t)$ nur in einigen Sonderfällen direkt und in einfacher Weise extrahiert werden.
- Das real nicht existierende äquivalente Tiefpass–Signal $x_{\rm TP}(t)$ ist ein mathematisches Hilfsmittel, mit dem die Zeitverläufe $a(t)$ und $\phi (t)$ durch einfache geometrische Überlegungen bestimmt werden können. Im Buch Modulation Methods werden wir darauf zurückkommen.
- Das analytische Signal $x_+(t)$ ist ein Zwischenschritt beim Übergang von $x(t)$ auf $x_{\rm TP}(t)$. Während $x_+(t)$ stets komplex ist, kann $x_{\rm TP}(t)$ in Sonderfällen reell sein, zum Beispiel bei idealer Amplitudenmodulation entsprechend dem Kapitel Zweiseitenband-Amplitudenmodulation (ZSB-AM).
Es gilt das gleiche Prinzip wie häufig in den Naturwissenschaften und Technik:
- Die Einführung von $x_+(t)$ und $x_{\rm TP}(t)$ bringt für einfache Probleme eher eine Verkomplizierung.
- Deren Vorteile erkennt man erst bei schwierigeren Aufgabenstellungen, die allein mit dem physikalischen Bandpass-Signal $x(t)$ nicht gelöst werden könnten oder nur mit sehr viel größerem Aufwand.
Zur weiteren Verdeutlichung stellen wir noch zwei interaktive Applets bereit:
- Physikalisches Signal & AnalytischesSignal ⇒ „Zeigerdiagramm”,
- Physikalisches Signal & Äquivalentes TP-Signal ⇒ „Ortskurve”.
Darstellung nach Real- und Imaginärteil
Insbesondere zur Beschreibung der Quadratur-Amplitudenmodulation (QAM) eignet sich die Darstellung des äquivalenten Tiefpass–Signals nach Real– und Imaginärteil:
- $$x_{\rm TP}(t) = x_{\rm I}(t)+ {\rm j} \cdot x_{\rm Q}(t).$$
In dieser Darstellung bezeichnet
- der Realteil $x_{\rm I}(t)$ die Inphasekomponente (Normalkomponente),
- der Imaginärteil $x_{\rm Q}(t)$ die Quadraturkomponente
von $x_{\rm TP}(t)$. Mit der Betragsfunktion $a(t) = |x_{\rm TP}(t)|$ und der Phasenfunktion $\phi (t) = \text{arc}\,x_{\rm TP}(t)$ entsprechend den Definitionen auf den vorangegangenen Seiten gilt:
- $$\begin{align*}x_{\rm I}(t) & = {\rm Re}[x_{\rm TP}(t)] = a(t) \cdot \cos (\phi(t)),\\ x_{\rm Q}(t) & = {\rm Im}[x_{\rm TP}(t)] = a(t) \cdot \sin (\phi(t)).\end{align*}$$
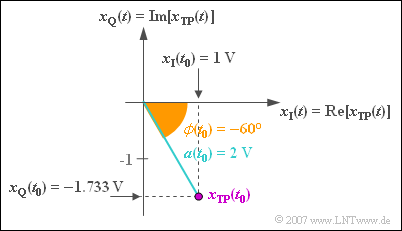
$\text{Beispiel 6:}$ Zum betrachteten Zeitpunkt $t_0$ gilt für das äquivalente Tiefpass–Signal:
- $$x_{\rm TP}(t = t_0) = 2\,{\rm V} \cdot {\rm e}^{- {\rm j \hspace{0.05cm}\cdot \hspace{0.05cm} 60 ^\circ} }.$$
Mit dem Satz von Euler kann hierfür geschrieben werden:
- $$x_{\rm TP}(t = t_0) = 2\,{\rm V} \cdot \cos(60 ^\circ) - {\rm j} \cdot 2\,{\rm V} \cdot \sin(60 ^\circ).$$
Damit gilt für die Inphasekomponente und für die Quadraturkomponente:
- $$x_{\rm I}(t = t_0) = 2\,{\rm V} \cdot \cos(60 ^\circ) = 1\text{V}, $$
- $$x_{\rm Q}(t = t_0) = \hspace{0.05cm} - {\rm j} \cdot 2\,{\rm V} \cdot \sin(60^\circ) =\hspace{0.05cm}-1.733\text{V}.$$
Durch Anwendung trigonometrischer Umformungen kann gezeigt werden, dass man das reelle, physikalische Bandpass–Signal auch in folgender Weise darstellen kann:
- $$x(t) = a(t) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi(t)) = x_{\rm I}(t)\cdot \cos (2 \pi \cdot f_{\rm T} \cdot t )-x_{\rm Q}(t)\cdot \sin (2 \pi \cdot f_{\rm T} \cdot t ). $$
Das Minuszeichen ergibt sich wegen der Verwendung der Phasenfunktion $\phi (t)$. Ein Vergleich mit der Seite Darstellung mit Cosinus- und Sinusanteil im zweiten Hauptkapitel zeigt, dass sich anstelle der Differenz die Summe ergibt, wenn man sich auf $\varphi (t) = -\phi (t)$ bezieht. Angepasst auf unser Beispiel erhält man dann:
- $$x(t) = a(t) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t - \varphi(t)) = x_{\rm I}(t)\cdot \cos (2 \pi \cdot f_{\rm T} \cdot t )+x_{\rm Q}(t)\cdot \sin (2 \pi \cdot f_{\rm T} \cdot t ).$$
Die Quadraturkomponente $x_{\rm Q}(t)$ unterscheidet sich gegenüber der oberen Gleichung also im Vorzeichen.
Ermittlung des äquivalenten TP-Signals aus dem BP-Signal
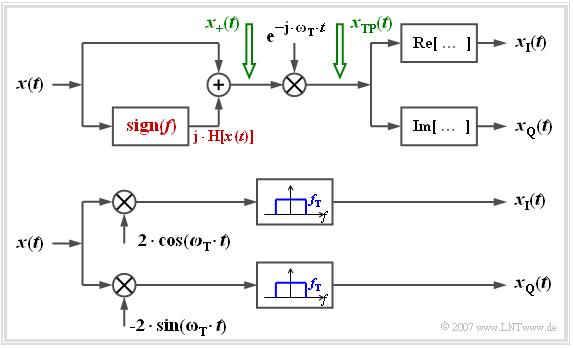
Die folgende Grafik zeigt zwei Anordnungen, um aus dem reellen Bandpass–Signal $x(t)$ das komplexe Tiefpass–Signal aufgespalten nach Inphase– und Quadraturkomponente zu ermitteln, beispielsweise zur Darstellung auf einem Oszilloskop. Betrachten wir zuerst das obere Modell:
- Hier wird zunächst das analytische Signal $x_+(t)$ durch Hinzufügen der Hilberttransformierten erzeugt.
- Durch Multiplikation mit der komplexen Exponentialfunktion (mit negativem Exponenten!) kommt man zum äquivalenten Tiefpass–Signal $x_{\rm TP}(t)$.
- Die gesuchten Komponenten $x_{\rm I}(t)$ und $x_{\rm Q}(t)$ erhält man dann durch Real– bzw. Imaginärteilbildung.
Bei der unteren (praxisrelevanteren) Anordnung erhält man für den oberen bzw. unteren Zweig nach den jeweiligen Multiplikationen:
- $$a(t)\cdot \cos (\omega_{\rm T} \cdot t + \phi(t)) \cdot 2 \cdot \cos (\omega_{\rm T} \cdot t ) = a(t)\cdot \cos ( \phi(t)) + \varepsilon_{\rm oben}(t),$$
- $$a(t)\cdot \cos (\omega_{\rm T} \cdot t + \phi(t)) \cdot (-2) \cdot \sin (\omega_{\rm T} \cdot t ) = a(t)\cdot \sin ( \phi(t)) + \varepsilon_{\rm unten}(t)).$$
Die jeweils zweiten Anteile liegen im Bereich um die doppelte Trägerfrequenz und werden durch die Tiefpässe mit jeweiliger Grenzfrequenz $f_{\rm T}$ entfernt:
- $$\varepsilon_{\rm oben}(t) = a(t)\cdot \cos (2\omega_{\rm T} \cdot t + \phi(t)),\hspace{0.8cm} \varepsilon_{\rm unten}(t) = - a(t)\cdot \sin (2\omega_{\rm T} \cdot t + \phi(t)).$$
Ein Vergleich mit obigen Gleichungen zeigt, dass am Ausgang die gewünschten Komponenten $x_{\rm I}(t)$ und $x_{\rm Q}(t)$ abgegriffen werden können:
- $$x_{\rm I}(t) = a(t)\cdot \cos ( \phi(t)) ,$$
- $$x_{\rm Q}(t) = a(t)\cdot \sin ( \phi(t)) .$$
Leistung und Energie eines Bandpass-Signals
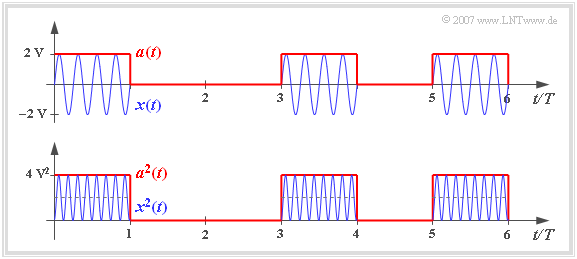
Wir betrachten das (blaue) Bandpass-Signal $x(t)$ gemäß der Grafik, das sich zum Beispiel bei Binary Amplitude Shift Keying ergibt. Dieses digitale Modulationsverfahren ist auch bekannt unter dem Namen On–Off–Keying.
Die auf $1 \,\Omega$ bezogene Signalleistung ergibt sich nach den Ausführungen auf der Seite Energiebegrenzte und leistungsbegrenzte Signale zu
- $$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{+T_{\rm M}/2} _{-T_{\rm M}/2}\hspace{-0.1cm} x^2(t)\,{\rm d}t.$$
Sind die binären Nullen und Einsen gleichwahrscheinlich, so kann man auf den unendlichen Integrationsbereich und den Grenzübergang verzichten, und man erhält für das oben skizzierte Mustersignal $x(t)$:
- $$P_x = \frac{1}{2T} \cdot \int ^{2T} _{0} x^2(t)\,{\rm d}t = \frac{4\,{\rm V}^2}{2T} \cdot \int^{T} _{0} \cos^2(\omega_{\rm T} \cdot t)\,{\rm d}t= 1\,{\rm V}^2.$$
Aus der unteren Skizze ist zu erkennen, dass man durch Mittelung über die quadrierte Hüllkurve $a^2(t)$ – also über das Betragsquadrat des äquivalenten Tiefpass–Signals $x_{\rm TP}(t)$ – ein doppelt so großes Ergebnis erhält. Deshalb gilt in gleicher Weise:
- $$P_x = { {1}/{2} \hspace{0.08cm}\cdot }\lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} |x_{\rm TP}(t)|^2\,{\rm d}t = {{1}/{2} \hspace{0.08cm}\cdot }\lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} a^2(t)\,{\rm d}t.$$
Dieses Resultat lässt sich verallgemeinern und es auch auf energiebegrenzte Signale anwenden. In diesem Fall gilt für die Energie entsprechend der Seite Energiebegrenzte und leistungsbegrenzte Signale:
- $$E_x = \int ^{+\infty} _{-\infty} x^2(t)\,{\rm d}t = { {1}/{2} \hspace{0.08cm}\cdot }\int ^{+\infty} _{-\infty} |x_{\rm TP}(t)|^2\,{\rm d}t = { {1}/{2} \hspace{0.08cm}\cdot }\int ^{+\infty} _{-\infty} a^2(t)\,{\rm d}t.$$
Diese Gleichung gilt allerdings nur dann exakt, wenn die Trägerfrequenz $f_{\rm T}$ sehr viel größer als die Bandbreite $B_{\rm BP}$ des Bandpasses ist.
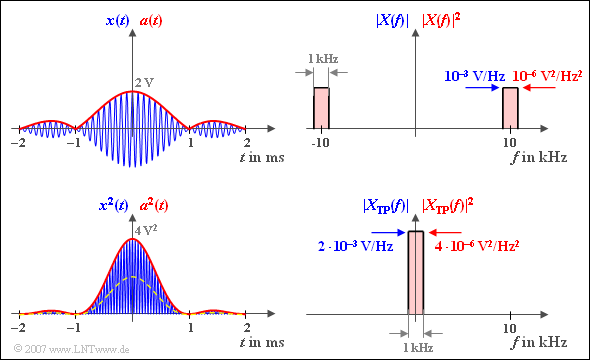
$\text{Beispiel 7:}$ Wir betrachten das in der Grafik links oben blau skizzierte Bandpass–Signal $x(t)$ mit $A = 2\,\text{V}$, $B = 1\,\text{kHz}$ und $f_{\rm T} = 10\,\text{kHz}$:
- $$x(t) = A \cdot {\rm si}(\pi \cdot B \cdot t) \cdot \cos(2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t + \phi(t)).$$
Oben rechts ist das zum Signal $x(t)$ gehörige Betragsspektrum $\vert X(f) \vert$ dargestellt. Es gilt die blaue Beschriftung:
- $X(f)$ ist aufgrund der Symmetrieverhältnisse rein reell:
- $$\vert X(f) \vert = X(f).$$
- $\vert X(f) \vert$ setzt sich also aus zwei Rechtecken um $\pm f_{\rm T}$ zusammen.
- Im Bereich um die Trägerfrequenz gilt:
- $$\vert X(f) \vert = A/(2B) = 10^{-3}\text{V/Hz}.$$
Die Energie dieses Bandpass–Signals könnte prinzipiell nach folgender Gleichung berechnet werden:
- $$E_x = \int^{+\infty} _{-\infty} A^2 \cdot \frac{ {\rm sin}^2(\pi \cdot B \cdot t)}{ (\pi \cdot B \cdot t)^2}\cdot \cos^2(2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t + \phi(t))\,{\rm d}t .$$
Entsprechend den obigen Gleichungen gilt mit der oben links rot eingezeichneten Hüllkurve $a(t)$ aber auch:
- $$E_x = { {1}/{2} \hspace{0.08cm}\cdot }\int^{+\infty} _{-\infty} a^2(t)\,{\rm d}t= { {1}/{2} \hspace{0.08cm}\cdot }\int^{+\infty} _{-\infty} \vert A \cdot {\rm si}(\pi \cdot B \cdot t)\vert^2\,{\rm d}t $$
- $$\Rightarrow \hspace{0.3cm} E_x = A^2\cdot \int^{+\infty} _{0} {\rm si}^2(\pi \cdot B \cdot t)\,{\rm d}t =A^2\cdot \frac {\pi}{2}\cdot \frac {1}{\pi B} = \frac {A^2}{2 B}= 2 \cdot 10^{-3}\,{\rm V}^2/{\rm Hz}.$$
Aus dieser Gleichung erkennt man sofort, dass die Signalenergie $E_x$ unabhängig von der Trägerphase $\phi$ ist.
Eine zweite Lösungsmöglichkeit mit gleichem Ergebnis bietet schließlich der Satz von Parseval:
- $$\int ^{+\infty} _{-\infty} a^2(t)\,{\rm d}t= \int ^{+\infty} _{-\infty} \vert A(f) \vert ^2\,{\rm d}f \hspace{0.3cm} \Rightarrow \hspace{0.3cm} E_x = {1}/{2}\cdot ( {A}/{B})^2 \cdot B = {A^2}/(2 B).$$
Hierbei ist berücksichtigt:
- Es gilt $\vert A(f) \vert = \vert X_{\rm TP}(f) \vert $.
- Innerhalb der Bandbreite $B$ um die Frequenz $f = 0$ ist $X_{\rm TP}(f)$ doppelt so groß wie $X(f)$ um die Frequenz $f = f_{\rm T}$, nämlich $A/B$.
- Dies hängt mit der Definition des Spektrums $X_+(f)$ des analtischen Signals zusammen, aus dem $X_{\rm TP}(f)$ durch Verschiebung entsteht.
Aufgaben zum Kapitel
Aufgabe 4.5: Ortskurve bei ZSB-AM
Aufgabe 4.5Z: Einfacher Phasenmodulator
Aufgabe 4.6: Ortskurve bei ESB-AM
Aufgabe 4.6Z: Ortskure bei Phasenmodulation