Equivalent Low-Pass Signal and its Spectral Function

1 Motivation for Describing in the Equivalent Low Pass Range
2 Definition in the Frequency Domain
3 Description in The Time Domain
4 Definition of The Locus Curve
5 Representing with Magnitude and Phase
6 Relation Between Equivalent LP-Signal and BP-Signal
7 Why Multiple Representations of The Same Signal Exist
8 Representation According to Real and Imaginary Part
9 Determination of the equivalent TP signal from the BP signal
10 Power and Energy of a Bandpass Signal
11 Exercises for The Chapter

Motivation for Describing in the Equivalent Low Pass Range

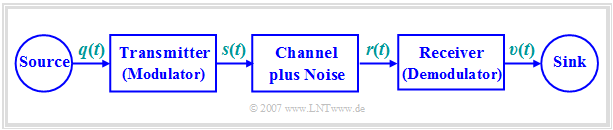
The following figure shows a possible structure of a message transmission system:

Often the low frequency source signal $q(t)$ is converted into a bandpass signal $s(t)$ ⇒ 'modulation.
After transmission, the received signal $r(t)$ - compared to the transmit signal $s(t)$ possibly distorted and with (noise) interference applied - must be reset to the original frequency range ⇒ 'Demodulation.
The sink signal $v(t)$, which should match the source signal $q(t)$ as closely as possible, is then again a low pass signal.

Block Diagram of a Bandpass Transmission System

Modulation and demodulation are therefore fundamental components of a transmission system, which are dealt with in detail in the book Modulation Methods . A short summary can be found in the first chapter Principles of Message Transmission of this book.

The investigation, simulation, optimization, and dimensioning of bandpass systems are mostly done in the 'equivalent low pass range, for which the following reasons can be given

If quality characteristics (bandwidth efficiency, signal-to-noise ratio, bit error rate, power requirements, etc.) of a low pass system are known, the corresponding values of related bandpass systems can be derived from them relatively easily. Examples are the digital modulation methods Amplitude Shift Keying (ASK) and Binary Phase Shift Keying (BPSK), whose performance variables can be "extrapolated" from the comparable baseband system (i.e., without modulator and demodulator).

Individual subchannels in a so-called frequency division multiplex system, which differ by different carrier frequencies, can often be considered qualitatively equivalent. Therefore, it is sufficient to limit the calculation and dimensioning to a single channel and to perform these investigations in the equivalent low-pass range - i.e. without considering the specific carrier frequency.

t is often the case that the bandwidth of a communication connection is orders of magnitude smaller than the carrier frequency. For example, in the GSM standard&nbsp the individual channels are located in the frequency range around $900\ \rm MHz$ („D-Network”) and $1800\ \rm MHz$ („E-Network”), while each channel has only a small bandwidth of $200\ \rm kHz$ available. Therefore a simulation in the equivalent low pass range is much less complex than a simulation of the corresponding bandpass signals.

Definition in the Frequency Domain

We consider a real bandpass signal $x(t)$ with the spectrum $X(f)$. Furthermore we want to apply:

The bandpass signal $x(t)$ is said to result from the modulation of a low-frequency message signal $q(t)$ with the carrier signal $z(t)$ the frequency $f_{\rm T}$ . The type of modulation (whether analog or digital, amplitudes– or angle modulation, single sideband or double sideband) is not specified.
The spectral function $X_+(f)$ of the corresponding analytical signal $x_+(t)$ exists only for positive frequencies and is twice as large as $X(f)$. For the derivation of $X_+(f)$ the carrier frequency $f_{\rm T}$ of the system does not need be known.

$\text{Definition:}$ If the spectrum of the analytical signal $x_+(t)$ is shifted to the left for $f_{\rm T}$ , the result is called the Spectrum of the Equivalent Low-Pass Signal:

$$X_{\rm TP}(f) = X_{\rm +}(f + f_{\rm T}).$$

In general $X(f)$, $X_+(f)$ and $X_{\rm TP}(f)$ are complex-valued. However, if $X(f)$ is purely real, then the spectral functions $X_+(f)$ and $X_{\rm TP}(f)$ are also purely real, because they result from $X(f)$ only from the operations "Cut and Double" or "Frequency Shift" respectively.

}

For the calculation of the equivalent low-pass spectrum $X_{\rm TP}(f)$ - in contrast to $X_+(f)$ - the knowledge of the carrier frequency $f_{\rm T}$ is absolutely necessary. For other values of $f_{\rm T}$ other low-pass spectra will also result.

If one transforms the above equation into the time domain, one obtains after applying the shifting theorem:

$$x_{\rm TP}(t) = x_{\rm +}(t)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}.$$

The relation $x(t) = \text{Re}\big[x_+(t)\big]$ yields the procedure to determine the actual physical bandpass signal from the equivalent lowpass signal:

$$x(t) = {\rm Re}[x_{\rm +}(t)] = {\rm Re}\big[x_{\rm TP}(t)\cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot 2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_{\rm T}\hspace{0.05cm} \cdot \hspace{0.05cm} \hspace{0.05cm}t}\big].$$

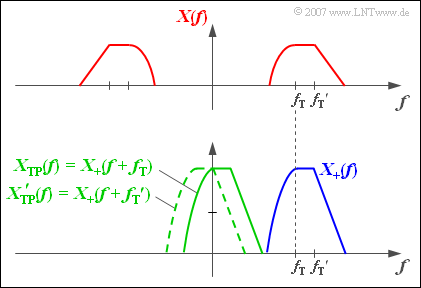
$\text{Example 1:}$ The upper figure shows the purely real spectral function $X(f)$ of a bandpass signal $x(t)$ which is the result of modulating a low frequency signal $q(t)$ with the carrier frequency $f_{\rm T}$ .

Construction of The Equivalent Low Pass Signals
in The Frequeny Domain

Below that, the two likewise real spectral functions $X_+(f)$ and $X_{\rm TP}(f)$ are shown. Due to the asymmetries concerning the frequency origin $(f = 0)$ the corresponding time functions are complex.

The continuous green spectral function $X_{\rm TP}(f)$ is shifted to the left with respect to $X_{+}(f)$ by the carrier frequency $f_{\rm T}$ .

If the spectrum $X(f)$ is the modulation result of another message signal $q\hspace{0.05cm}'(t)$ with a different carrier frequency ${f_{\rm T} }\hspace{0.05cm}'$, this would also result in another equivalent TP signal ${X_{\rm TP} }\hspace{0.05cm}'(f)$.

An exemplary spectral function ${X_{\rm TP} }\hspace{0.05cm}'(f)$ is drawn in the graphic with green-dashed lines.

Description in The Time Domain

To simplify the representation we now assume a line spectrum, so that the analytical signal can be represented as 'pointer compound ⇒ sum of complex rotating pointers:

$$X_{+}(f) = \sum_{i=1}^{I} {A_i} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_i}\cdot\delta (f - f_i) \hspace{0.3cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} x_{+}(t) = \sum_{i=1}^{I} A_i \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}( 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_i\hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$

By shifting the frequency by $f_{\rm T}$ to the left the equivalent low pass signal in frequency and time domain is thus:

$$X_{\rm TP}(f) = \sum_{i=1}^{I} {A_i} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_i}\cdot\delta (f - \nu_i)\hspace{0.3cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} x_{\rm TP}(t) = \sum_{i=1}^{I} A_i \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}( 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu_i \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$

The following relation is valid between the frequency values $f_i$ and $\nu_i$ $(i = 1, \ \text{...} \ , I)$:

$$\nu_i = f_i - f_{\rm T} .$$

These equations can be interpreted as follows:

At time $t = 0$ the equivalent low-pass signal is identical to the analytical signal:

$$x_{\rm TP}(t = 0) = x_{\rm +}(t = 0)= \sum_{i=1}^{I} A_i \cdot {\rm e}^{{-\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_i}.$$

At this point in time, the pointer group is thus defined by the $I$ amplitude parameter $A_i$ and the $I$ phase positions $\varphi_i$ alone.
All pointers of the analytical signal $x_+(t)$ rotate for $t > 0$ corresponding to the (always positive) frequencies $f_i$ counterclockwise.
For the equivalent low-pass signal, the rotation speeds are lower. Hands with $\nu_i > 0$ turn in mathematically positive direction (counterclockwise), those with $\nu_i < 0$ in counterclockwise direction (clockwise).
If the frequency parameter is $\nu_i = 0$ for a pointer, this pointer rests in the complex plane corresponding to its initial position.

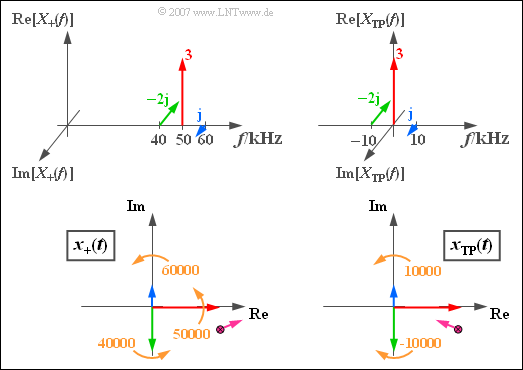
$\text{Example 2:}$ We consider a spectrum consisting of three spectral lines at $40\,\text{kHz}$, $50\,\text{kHz}$ and $60\,\text{kHz}$ consisting of spectrum $X_+(f)$. With the amplitude and phase parameters recognizable from the graphic you obtain the analytical signal $x_+(t)$ corresponding to the lower left sketch.

Construction of The Equivalent Low Pass Signals in The Time Domain

The snapshot of the lower left graph ⇒ analytical signal $x_+(t)$ applies to the time $t = 0$. All hands then turn counterclockwise at a constant angular velocity.

The blue pointer rotates with $60000$ rotations per second are fastest and the green pointer rotates with the angular frequency $\omega_{40} = 2\pi \cdot 40000 \hspace{0.1cm} 1/\text{s}$ is the slowest.
The violet sum point of all three pointers moves for $t > 0$ in the complex plane in a complicated manner, for the above numerical values first roughly in the direction drawn.

The graphics on the right describe the equivalent low-pass signal in the frequency domain (top) and in the time domain (bottom), valid for $f_{\rm T} = 50\,\text{kHz}$.

The carrier is now at $f = 0$ and the corresponding red rotating pointer does not move.
The blue pointer (OSB) rotates here with $\omega_{10} = 2\pi \cdot 10000 \hspace{0.1cm}1/\text{s}$ counterclockwise.
The green pointer (USB) rotates counterclockwise at the same speed ($-\omega_{10}$).

Definition of The Locus Curve

$\text{Definition:}$ As locus curve we call the curve on which the equivalent low-pass signal $x_{\rm TP}(t)$ moves in the complex plane

Notes: In other technical literature this term is rarely used. Therefore, initially, an example is shown.

Definition of The Locus Curve

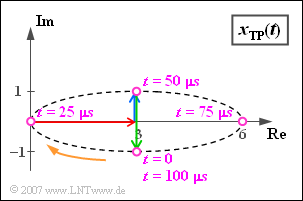
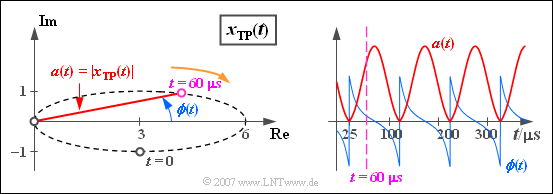
$\text{Example 3:}$ We consider the equivalent low-pass signal $x_{\rm TP}(t)$ of $\text{Example 2}$, consisting of

the resting pointer of length $3$ (red)
the pointer with $\omega_{10} = 2\pi \cdot 10000 \hspace{0.1cm} 1/\text{s}$ in mathematical positive direction rotating blue pointer with the complex amplitude j,
the green pointer of length $2$, which is currently $t = 0$ in the direction of the negative imaginary axis. This rotates with the same angular velocity $\omega_{10}$ as the blue pointer, but in the opposite direction ($-\omega_{10}$).

The blue and the green pointer each require exactly one period duration $T_0 = 100 \,{\rm µ}\text{s}$ for one rotation. The further course of the process can be seen in the above illustration:

The violet pointer sum is at time $t = 0$ equals $3 - \text{j}$.
After $t = T_0/4 = 25 \,{\rm µ}\text{s}$ the resulting pointer group has the value „Null”, since now the two rotating pointers lie in the opposite direction to the carrier and compensate it exactly.
After a period $(t = T_0 = 100 \,{\rm µ}\text{s})$ the initial state is reached again: $x_{\rm TP}(t = T_0) = x_{\rm TP}(t=0) = 3 - \text{j}$.

exactly.

After a period $(t = T_0 = 100 \,{\rm µ}\text{s})$ the initial state is reached again: $x_{\rm TP}(t = T_0) = x_{\rm TP}(t=0) = 3 - \text{j}$.}}}

In this example the locus curve is an ellipse, which is traversed by the equivalent low pass signal once per period.

The representation applies to the Double Sideband Amplitude Modulation with Carrier of a sinusoidal $10\ \rm kHz$ signal with a cosinusoidal carrier of any frequency, where the upper sideband (blue pointer) is attenuated.
If the lengths of the blue and the green rotating pointer were equal, the locus curve would be a horizontal one on the real axis - see Task 4.5.
In the book Modulation Methods the locus curves of different system variants are treated in detail.

In this example the locus curve is an ellipse, which is traversed by the equivalent low pass signal once per period.

The representation applies to the Double-Sideband–Amplitude Modulation with Carrier of a sinusoidal $10\ \rm kHz$ signal with a cosinusoidal carrier of any frequency, where the upper sideband (blue pointer) is attenuated.
If the lengths of the blue and the green rotating pointer were equal, the locus curve would be a horizontal one on the real axis - see Task 4.5.
In the book Modulation Methods ,the locus curves of different system variants are treated in detail.

Representing with Magnitude and Phase

The equivalent low-pass signal of the band-pass signal $x(t)$ is generally complex and can therefore be expressed in the form

$$x_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t)}$$.

Note the plus sign in the argument of the exponential function, which differs from the Complex Fourier Series . This is because the equation with the positive sign for the phase is usually used to describe the modulation method for the physical signal as well:

$$x(t) = a(t) \cdot {\cos} ( 2 \pi f_{\rm T} t + \phi(t)).$$

In many textbooks this equation is used with plus or minus signs depending on the application, but always with the same „phase identifier”. By using two different symbols $(\varphi$ and $\phi)$ we try to avoid this ambiguity in our learning tutorial $\rm LNTww$.

$\text{Example 4:}$ The same prerequisites apply as in the $\text{second example }$ and in the $\text{third one}$. InHowever, instead of the complex function $x_{\rm TP}(t)$ the two real functions $a(t)$ and $\phi(t)$ are now displayed in the graphic.

Magnitude and Phase of The Equivalent Lowpass-Signal

It should be noted that this is a representation:

The Magnitude function shows the time dependence of the pointer length:

$$a(t)= \vert x_{\rm TP}(t)\vert =\sqrt{ {\rm Re}\left[x_{\rm TP}(t)\right]^2 + {\rm Im}\left[x_{\rm TP}(t)\right]^2 }.$$

The magnitude function $a(t)$ is in this example like the complex equivalent low pass signal $x_{\rm TP}(t)$ periodic with $T_0$ and takes values between $0$ and $6$ .

The phase function describes the time-dependent angle of the equivalent low pass signal $x_{\rm TP}(t)$, related to the coordinate origin:

$$\phi(t)= {\rm arc} \left[x_{\rm TP}(t)\right]= {\rm arctan} \hspace{0.1cm}\frac{ {\rm Im}\left[x_{\rm TP}(t)\right]}{ {\rm Re}\left[x_{\rm TP}(t)\right]}.$$

Hier noch einige numerische Ergebnisse für die Phasenwerte: Here are some numerical results for the phase values:

The phase at start time is $\phi (t = 0) =\hspace{0.1cm} -\arctan (1/3) ≈ \hspace{0.1cm} -18.43^{\circ} = \hspace{0.1cm}-0.32\,\text{rad}$.
At $t = 25\,{\rm µ}\text{s}$ as well as at all equidistant times thereof in the distance $T_0 = 100 \,{\rm µ}\text{s}$ is $x_{\rm TP}(t) = 0$ so that at these times the phase $\phi(t)$ changes abruptly from $-\pi /2$ to $+\pi /2$ .
At the time $t = 60\,{\rm µ}\text{s}$ the phase has a slightly positive value.

Relation Between Equivalent LP-Signal and BP-Signal

A bandpass signal $x(t)$ resulting from the modulation of a low-frequency message signal $q(t)$ with a carrier signal $z(t)$ of frequency $f_{\rm T}$ can be represented as follows:

$$x(t) = a(t) \cdot {\cos} ( 2 \pi f_{\rm T} t + \phi(t)) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} x_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t)}.$$

It should be noted here:

$a(t)$ is the time-dependent amplitude, which is often also called envelope . This is equal to the amount $|x_{\rm TP}(t)|$ of the equivalent low pass signal.
$\phi(t)$ is the 'phase function, i.e., the time-dependent phase, which can also be determined from the equivalent low-pass signal as the angle to the coordinate origin of the complex plane.
In the physical signal $x(t)$ , the phase $\phi(t)$ can be recognized by the 'zero crossings. With $\phi(t) > 0$ the zero crossing occurs in $x(t)$ in the range of time $t$ earlier than with the carrier signal $z(t)$. In contrast, $\phi(t) < 0$ means a shift of the zero crossing to a later time.
One speaks of 'amplitude modulation if all information about the message signal is contained in the envelope $a(t)$ while $\phi(t)$ is constant.
Conversely, with Phase modulation the phase function $\phi(t)$ contains all information about the message signal, while $a(t)$ is constant.

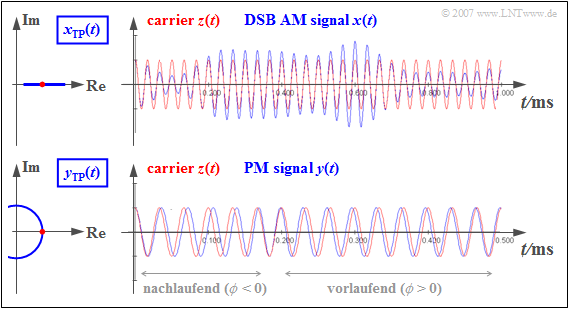
$\text{Example 5:}$ The upper part of the following figure describes the Double Sideband Amplitude Modulation (DSB-AM) With Carrier:

The equivalent TP signal $x_{\rm TP}(t)$ is here always real ⇒ the locus curve is a horizontal straight line.
Therefore the zero crossings of the blue DSB-AM signal $x(t)$ correspond exactly to those of the red carrier signal $z(t)$ .
This means: the phase function $\phi(t)$ is identical to zero ⇒ the envelope $a(t)$ contains all information about the message signal.

$x_{\rm TP}(t)$ For Double-Sideband Amplitude Modulation and Phase Modulation

However, the lower part of the graphic applies to the Phase Modulation (PM):

The PM signal $y(t)$ always has a constant envelope ⇒ the locus curve is an arc.
The phase value here is initially smaller than zero ⇒ the $y(t)$–zero crossings occur later than those of the carrier $z(t)$ ⇒ the zero crossings are "trailing".
For positive values of the message signal also $\phi (t) > 0$ ⇒ the zero crossings occur earlier than those of the carrier signal ⇒ they are "leading".
With phase modulation, therefore, all information about the message signal $q(t)$ is contained in the positions of the zero crossings.

Why Multiple Representations of The Same Signal Exist

Finally, and hopefully not too late, we want to turn to the question why the two complex and less comprehensible signals $x_+(t)$ and $x_{\rm TP}(t)$ are actually necessary to describe the actual bandpass signal $x(t)$ . They were not introduced in communications engineering in order to unsettle students, but:

$\text{Conclusion:}$

The envelope curve $a(t)$ and the phase function $\phi (t)$ can be extracted directly and easily from the actual, physical BP signal $x(t)$ only in some special cases
The real non existing equivalent low-pass signal $x_{\rm TP}(t)$ is a mathematical tool to determine the time histories $a(t)$ and $\phi (t)$ by simple geometrical considerations. We will come back to this later in the book Modulation Methods .
The analytical signal $x_+(t)$ is an intermediate step in the transition from $x(t)$ to $x_{\rm TP}(t)$. While $x_+(t)$ is always complex, $x_{\rm TP}(t)$ can be real in special cases, for example, with ideal amplitude modulation according to the chapter Double-Sideband Amplitude Modulation (DSB-AM).

The same principle applies as often used in the natural sciences and technology:

The introduction of $x_+(t)$ and $x_{\rm TP}(t)$ brings rather a complication for simple problems.
The advantages of this approach can only be seen in more difficult problems, which could not be solved with the physical bandpass signal $x(t)$ alone or only with much more effort.

For further clarification we provide two interactive applets:

Physical & Analytical Signal ⇒ „Vector Diagram”,
Physical & Equivalent TP-Signal ⇒ „Loot Curve”.

Representation According to Real and Imaginary Part

Especially for the description of Quadrature Amplitude Modulation (QAM), the representation of the equivalent low pass signal according to real and imaginary part is suitable:

$$x_{\rm TP}(t) = x_{\rm I}(t)+ {\rm j} \cdot x_{\rm Q}(t).$$

In this representation,

the real part $x_{\rm I}(t)$ describes the in-phase component (normal component), whereas
the imaginary part $x_{\rm Q}(t)$ describes the 'quadrature component

of $x_{\rm TP}(t)$. With the absolute value function $a(t) = |x_{\rm TP}(t)|$ and the phase function $\phi (t) = \text{arc}\,x_{\rm TP}(t)$ according to the definitions on the previous pages:

$$\begin{align*}x_{\rm I}(t) & = {\rm Re}[x_{\rm TP}(t)] = a(t) \cdot \cos (\phi(t)),\\ x_{\rm Q}(t) & = {\rm Im}[x_{\rm TP}(t)] = a(t) \cdot \sin (\phi(t)).\end{align*}$$

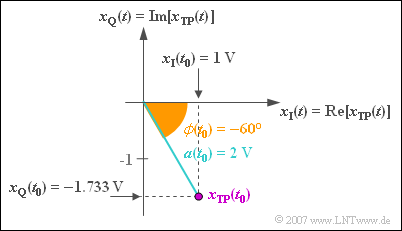
Real And Imaginary Part of The Equivalent Lowpass-Signal

$\text{Example 6:}$ At the considered time $t_0$ applies to the equivalent low pass signal:

$$x_{\rm TP}(t = t_0) = 2\,{\rm V} \cdot {\rm e}^{- {\rm j \hspace{0.05cm}\cdot \hspace{0.05cm} 60 ^\circ} }.$$

With the Euler's Theorem , it can be written like this:

$$x_{\rm TP}(t = t_0) = 2\,{\rm V} \cdot \cos(60 ^\circ) - {\rm j} \cdot 2\,{\rm V} \cdot \sin(60 ^\circ).$$

This applies to the in-phase and quadrature component:

$$x_{\rm I}(t = t_0) = 2\,{\rm V} \cdot \cos(60 ^\circ) = 1\text{V}, $$

$$x_{\rm Q}(t = t_0) = \hspace{0.05cm} - {\rm j} \cdot 2\,{\rm V} \cdot \sin(60^\circ) =\hspace{0.05cm}-1.733\text{V}.$$

By applying trigonometric transformations it can be shown that the real, physical bandpass signal can also be represented in the following way:

$$x(t) = a(t) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi(t)) = x_{\rm I}(t)\cdot \cos (2 \pi \cdot f_{\rm T} \cdot t )-x_{\rm Q}(t)\cdot \sin (2 \pi \cdot f_{\rm T} \cdot t ). $$

The minus sign results from the use of the phase function $\phi (t)$. A comparison with the page Representation With Cosine- and Sine Component in the second main chapter shows that instead of the difference, the sum results when referring to $\varphi (t) = -\phi (t)$ . Adapted to our example, you then get

$$x(t) = a(t) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t - \varphi(t)) = x_{\rm I}(t)\cdot \cos (2 \pi \cdot f_{\rm T} \cdot t )+x_{\rm Q}(t)\cdot \sin (2 \pi \cdot f_{\rm T} \cdot t ).$$

The quadrature component $x_{\rm Q}(t)$ thus differs from the above equation in the sign.

Determination of the equivalent TP signal from the BP signal

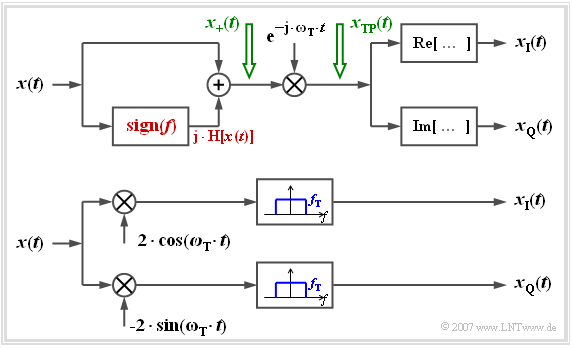
The following figure shows two arrangements to determine the complex low-pass signal split into inphase and quadrature components from the real bandpass signal $x(t)$ for display on an oscilloscope, for example Let us first look at the upper model:

The analytical signal $x_+(t)$ is first generated here by adding the Hilbert Transformed .
Multiplication with the complex exponential function (with negative exponent!) yields the equivalent low-pass signal $x_{\rm TP}(t)$.
The sought components $x_{\rm I}(t)$ and $x_{\rm Q}(t)$ are then obtained by forming real or imaginary parts.

Division of the Equivalent Low-Pass Signal Into In-phase and Quadrature Components

With the lower (more practical) arrangement, you get for the upper or lower branch after the respective multiplications:

$$a(t)\cdot \cos (\omega_{\rm T} \cdot t + \phi(t)) \cdot 2 \cdot \cos (\omega_{\rm T} \cdot t ) = a(t)\cdot \cos ( \phi(t)) + \varepsilon_{\rm oben}(t),$$

$$a(t)\cdot \cos (\omega_{\rm T} \cdot t + \phi(t)) \cdot (-2) \cdot \sin (\omega_{\rm T} \cdot t ) = a(t)\cdot \sin ( \phi(t)) + \varepsilon_{\rm unten}(t)).$$

The respective second parts are in the range around twice the carrier frequency and are removed by the low-pass filters with the respective cut-off frequency $f_{\rm T}$ :

$$\varepsilon_{\rm oben}(t) = a(t)\cdot \cos (2\omega_{\rm T} \cdot t + \phi(t)),\hspace{0.8cm} \varepsilon_{\rm unten}(t) = - a(t)\cdot \sin (2\omega_{\rm T} \cdot t + \phi(t)).$$

A comparison with the above equations shows that the desired components $x_{\rm I}(t)$ and $x_{\rm Q}(t)$ can be tapped at the output:

$$x_{\rm I}(t) = a(t)\cdot \cos ( \phi(t)) ,$$

$$x_{\rm Q}(t) = a(t)\cdot \sin ( \phi(t)) .$$

Power and Energy of a Bandpass Signal

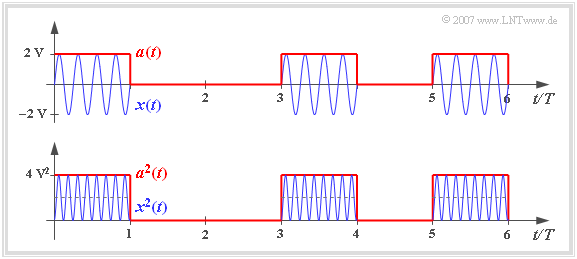
We look at the (blue) bandpass signal $x(t)$ according to the graph, which results for example from Binary Amplitude Shift Keying . This digital modulation method is also known as On-Off-Keying.

Power and Energy of a Bandpass Signal

The signal power related to $1 \,\Omega$ is given by the explanations on page Energy Limited and Power Limited Signals to

$$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{+T_{\rm M}/2} _{-T_{\rm M}/2}\hspace{-0.1cm} x^2(t)\,{\rm d}t.$$

If the binary zeros and ones are equally probable, then the infinite integration range and the boundary crossing can be omitted, and you get for the above sketched pattern signal

$$P_x = \frac{1}{2T} \cdot \int ^{2T} _{0} x^2(t)\,{\rm d}t = \frac{4\,{\rm V}^2}{2T} \cdot \int^{T} _{0} \cos^2(\omega_{\rm T} \cdot t)\,{\rm d}t= 1\,{\rm V}^2.$$

From the sketch below you can see that by averaging over the squared envelope $a^2(t)$ - i.e. over the magnitude square of the equivalent lowpass signal $x_{\rm TP}(t)$ - you get a result twice as large. Therefore the same holds here likewise:

$$P_x = { {1}/{2} \hspace{0.08cm}\cdot }\lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} |x_{\rm TP}(t)|^2\,{\rm d}t = {{1}/{2} \hspace{0.08cm}\cdot }\lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} a^2(t)\,{\rm d}t.$$

This result can be generalized and applied to energy limited signals. In this case, the energy according to page Energy Limited and Power Limited Signals:

$$E_x = \int ^{+\infty} _{-\infty} x^2(t)\,{\rm d}t = { {1}/{2} \hspace{0.08cm}\cdot }\int ^{+\infty} _{-\infty} |x_{\rm TP}(t)|^2\,{\rm d}t = { {1}/{2} \hspace{0.08cm}\cdot }\int ^{+\infty} _{-\infty} a^2(t)\,{\rm d}t.$$

However, this equation only applies exactly if the carrier frequency $f_{\rm T}$ is much larger than the bandwidth $B_{\rm BP}$ of the bandpass..

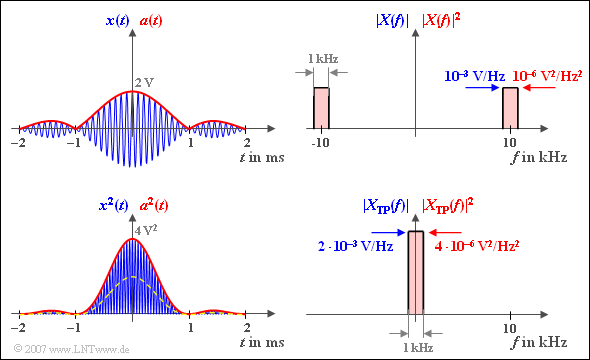
$\text{Example 7:}$ We look at the bandpass signal $x(t)$ with $A = 2\,\text{V}$, $B = 1\,\text{kHz}$ and $f_{\rm T} = 10\,\text{kHz}$:

Power Calculation in the Equivalent Lowpass Range

$$x(t) = A \cdot {\rm si}(\pi \cdot B \cdot t) \cdot \cos(2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t + \phi(t)).$$

The amount spectrum $x(t)$ belonging to the signal $x(t)$ $\vert X(f) \vert$ is displayed in the upper right corner. The blue label applies:

$X(f)$ is purely real due to the symmetry relations:

$$\vert X(f) \vert = X(f).$$

$\vert X(f) \vert$ s thus composed of two rectangles around $\pm f_{\rm T}$ .

In the range around the carrier frequency applies:

$$\vert X(f) \vert = A/(2B) = 10^{-3}\text{V/Hz}.$$
The energy of this bandpass signal could in principle be calculated by the following equation:

$$E_x = \int^{+\infty} _{-\infty} A^2 \cdot \frac{ {\rm sin}^2(\pi \cdot B \cdot t)}{ (\pi \cdot B \cdot t)^2}\cdot \cos^2(2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t + \phi(t))\,{\rm d}t .$$

According to the above equations, with the envelope curve $a(t)$ but also with the envelope curve&nbsp drawn in red in the upper left corner:

$$E_x = { {1}/{2} \hspace{0.08cm}\cdot }\int^{+\infty} _{-\infty} a^2(t)\,{\rm d}t= { {1}/{2} \hspace{0.08cm}\cdot }\int^{+\infty} _{-\infty} \vert A \cdot {\rm si}(\pi \cdot B \cdot t)\vert^2\,{\rm d}t $$

$$\Rightarrow \hspace{0.3cm} E_x = A^2\cdot \int^{+\infty} _{0} {\rm si}^2(\pi \cdot B \cdot t)\,{\rm d}t =A^2\cdot \frac {\pi}{2}\cdot \frac {1}{\pi B} = \frac {A^2}{2 B}= 2 \cdot 10^{-3}\,{\rm V}^2/{\rm Hz}.$$

According to the above equations, with the envelope $a(t)$ but also with the envelope drawn in red in the upper left corner:

A second solution with the same result is offered by the Parseval's theorem:

$$\int ^{+\infty} _{-\infty} a^2(t)\,{\rm d}t= \int ^{+\infty} _{-\infty} \vert A(f) \vert ^2\,{\rm d}f \hspace{0.3cm} \Rightarrow \hspace{0.3cm} E_x = {1}/{2}\cdot ( {A}/{B})^2 \cdot B = {A^2}/(2 B).$$

This is taken into account:

The following applies $\vert A(f) \vert = \vert X_{\rm TP}(f) \vert $.
Inside the bandwidth $B$ around the frequency $f = 0$ is $X_{\rm TP}(f)$ twice as large as $X(f)$ around the frequency $f = f_{\rm T}$, namely $A/B$.
This is related to the definition of the spectrum $X_+(f)$ the analemic signal from which $X_{\rm TP}(f)$ is created by shifting.