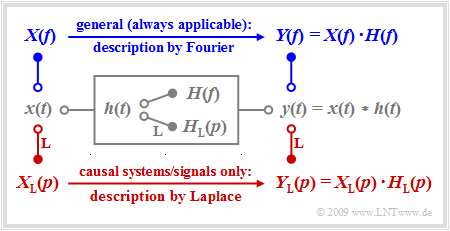
Considered system model
We consider a linear time-invariant system with the impulse response $h(t)$, to whose input the signal $x(t)$ is applied. The output signal $y(t)$ is then obtained as the convolution product $x(t) ∗ h(t)$.
For non-causal systems and signals, the first Fourier integral must always be applied to describe the spectral behavior, and the following is valid for the output spectrum:
- $$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$
The Fourier integral also continues to be valid for causal systems and signals, i.e. under the assumption
- $$x(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$
In this case, however, there are significant advantages in applying the Laplace transformation while taking into account certain restrictions:
- The systems treated in this way are always realizable by a circuit. The developer is not tempted to offer unrealistic solutions.
- The Laplace transform $X_{\rm L}(p)$ is always a real function of the spectral variable $p$. The fact that this variable is derived from the multiplication of the physical angular frequency $ω = 2πf$ by the imaginary unit $\rm j$ according to $p = {\rm j} · 2πf$ does not matter for the user.
- The implicit condition $x(t) = 0$ for $t < 0$ specifically allows for simpler analysis of transient behavior after switching-on processes than with the Fourier integral.
Definition of the Laplace transformation
Starting from the first Fourier integral
- $$X(f) = \int_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t,$$
the Laplace transformation is obtained directly using the formal substitution $p = {\rm j} · 2πf$ for a causal time function
- $$x(t) = 0 \ \ \text{for} \ \ t < 0.$$
$\text{Definition:}$ The Laplace transform of a causal time function $x(t)$ is:
- $$X_{\rm L}(p) = \int_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t} }\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm briefly}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}.$$
The relationship between the Laplace transform $X_{\rm L}(p)$ and the physical spectrum $X(f)$ is often given as follows:
- $$X(f) = X_{\rm L}(p) \Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}={\rm \hspace{0.05cm} j\hspace{0.05cm}2\pi \it f}}}.$$
- However, if the signal $x(t)$ has periodic components and thus the spectral function $X(f)$ contains Dirac functions, then this equation is not applicable.
- In this case, $p = α + {\rm j} · 2πf$ must be applied and then the limit $α → 0$ must be formed.
$\text{Example 1:}$ We assume the unilaterally and exponentially decreasing time function corresponding to the sketch in $\text{Example 1}$ of the chapter "Conclusions from the Allocation Theorem":
- $$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$
Thus, the Laplace transform is:
- $$X_{\rm L}(p) = \int_{0}^{\infty} {\rm e}^{-t/T} \cdot {\rm e}^{-pt} \hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.08cm}\cdot \hspace{0.08cm}t}}\hspace{0.15cm}\Bigg \vert_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$
Considering $p = {\rm j} · 2πf$, the conventional spectral function with respect to $f$ is obtained:
- $$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$
In contrast, if we consider the frequency response of a low-pass filter of first-order whose impulse response $h(t)$ differs from the above time function by the factor $1/T$ , then the following holds for the Laplace transform and the Fourier transform, respectively:
- $$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT} } = \frac {1}{1+{\rm j} \cdot f/f_{\rm G} } \hspace{0.05cm} .$$
Often, as in this equation, the 3dB cut-off frequency $f_{\rm G} = 1/(2πT). <div style="clear:both;"> </div> </div> is used instead of the parameter $T$ . =='"`UNIQ--h-2--QINU`"'Some important Laplace correspondences== <br> Some important Laplace correspondences are compiled subsequently. All time signals $x(t)$ considered here are assumed to be dimensionless. For this reason, $X_{\rm L}(p)$ dann als Integral über die Zeit stets the unit "second". [[File:EN_LZI_T_3_2_S3.png |center|frame| Table with some Laplace transforms|class=fit]] *The Laplace transform of the [[Signal_Representation/Special_Cases_of_Impulse_Signals#Diracimpuls|Dirac function]] $δ(t)$ is $X_{\rm L}(p) = 1$ $($Diagramm $\rm A)$. Durch Anwendung des [[Signal_Representation/Fourier_Transform_Laws#Integrationssatz|Integrationssatzes]] erhält man $X_{\rm L}(p) = 1/p$ für die Sprungfunktion $γ(t)$ $($Diagramm $\rm B)$ und aus dieser durch Multiplikation mit $1/(pT)$ die Laplace–Transformierte der linear ansteigenden Funktion $x(t) = t/T$ für $t > 0$ $($Diagramm $\rm C)$. *The [[Signal_Representation/Special_Cases_of_Impulse_Signals#Rechteckimpuls|Rechteckfunktion]] kann aus der Subtraktion zweier um $T$ auseinanderliegender Sprungfunktionen $γ(t)$ und $γ(t – T)$ erzeugt werden, so dass sich nach dem [[Signal_Representation/Fourier_Transform_Laws#Verschiebungssatz|Verschiebungssatz]] die Laplace–Transformierte $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ ergibt $($Diagramm $\rm D)$. Durch Integration erhält man daraus die Rampenfunktion bzw. nach Multiplikation mit $1/(pT)$ deren Laplace–Transformierte $($Diagramm $\rm E)$. *Die Exponentialfunktion $($Diagramm $\rm F)$ wurde bereits auf der [[Linear_and_Time_Invariant_Systems/Laplace–Transformation_und_p–Übertragungsfunktion#Definition_der_Laplace.E2.80.93Transformation|letzten Seite]] betrachtet. Mit dem Faktor $1/T$ ist diese gleichzeitig die Impulsantwort eines Tiefpasses erster Ordnung. Durch Quadrierung erhält man die $p$–Spektralfunktion eines Tiefpasses zweiter Ordnung mit der Zeitfunktion $x(t) = t/T · {\rm e}^{–t/T}$ (Diagramm $\rm G$). *Neben der kausalen $\rm si$–Funktion $($Diagramm $\rm H)$ sind in der Tabelle auch die Laplace–Transformierten der kausalen Cosinus– und Sinusfunktion $($Diagramme $\rm I$ und $\rm J)$ angegeben, die sich zu $p/(p^2 + ω_0^2)$ bzw. $ω_0/(p^2 + ω_0^2)$ ergeben. Hierbei bezeichnet $ω_0 = 2πf_0 = 2π/T$ die so genannte Kreisfrequenz. =='"`UNIQ--h-3--QINU`"'Pol–Nullstellen–Darstellung von Schaltungen== <br> Ein jedes [[Lineare_zeitinvariante_Systeme|lineare zeitinvariante System]] (LZI), das durch eine Schaltung aus diskreten zeitkonstanten Bauelementen wie *Widerständen $(R)$, *Kapazitäten $(C)$, *Induktivitäten $(L)$ und *Verstärkerelementen realisiert werden kann, besitzt eine gebrochen–rationale '''$p$–Übertragungsfunktion''': :'"`UNIQ-MathJax12-QINU`"' Alle Koeffizienten des Zählers ⇒ $A_Z, \text{...} \ , A_0$ und des Nenners ⇒ $B_N, \text{...} , B_0$ sind reell. Weiter bezeichnen mit *$Z$ den Grad des Zählerpolynoms $Z(p)$, *$N$ den Grad des Nennerpolynoms $N(p)$. <div class="bluebox"> $\text{Äquivalente Pol–Nullstellen–Darstellung:}$ Für die $p$–Übertragungsfunktion kann auch geschieben werden: :'"`UNIQ-MathJax13-QINU`"' Die $Z + N + 1$ Parameter bedeuten: *$K = A_Z/B_N$ ist ein konstanter Faktor. Gilt $Z = N$, so ist dieser dimensionslos. *Die Lösungen der Gleichung $Z(p) = 0$ ergeben die $Z$ Nullstellen $p_{\rm o1},\text{...} \ , p_{\rm oZ}$ von $H_{\rm L}(p)$. *Die Nullstellen des Nennerpolynoms $N(p)$ liefern die $N$ Polstellen (oder kurz Pole). <div style="clear:both;"> </div> </div> Die Umformung ist eindeutig. Dies erkennt man daran, dass die $p$–Übertragungsfunktion gemäß der ersten Gleichung ebenfalls nur durch $Z + N + 1$ freie Parameter bestimmt ist, da einer der Koeffizienten $A_Z, \text{...} \ , A_0, B_N, \text{...} \ , B_0$ ohne Änderung des Quotienten auf $1$ normiert werden kann. <div class="greybox"> $\text{Example 2:}$ Wir betrachten den gezeichneten Vierpol mit einer Induktivität $L$ $($komplexer Widerstand $pL)$ im Längszweig sowie im Querzweig die Serienschaltung eines Ohmschen Widerstandes $R$ und einer Kapazität $C$ mit dem komplexen Widerstand $1/(pC)$. [[File:P_ID1759__LZI_T_3_2_S4_neu.png|center|frame|Betrachteter Vierpol und dazugehöriges Pol–Nullstellen–Diagramm|class=fit]] Damit lautet die $p$–Übertragungsfunktion: :'"`UNIQ-MathJax14-QINU`"' Setzt man $p = {\rm j} · 2πf$ ein, so erhält man die Fourier–Übertragungsfunktion (bzw. den Frequenzgang). Dividiert man in obiger Gleichung Zähler und Nenner durch $LC$, so ergibt sich: :'"`UNIQ-MathJax15-QINU`"' Im rechten Gleichungsteil ist die Übertragungsfunktion $H_{\rm L}(p)$ in Pol–Nullstellen–Notation angegeben. Durch Koeffizientenvergleich ergeben sich für $R = 50 \ \rm Ω$, $L = 25\ \rm µ H$ und $C = 62.5 \ \rm nF$ folgende Werte: *die Konstante $K = R/L = 2 · 10^6 \cdot 1/{\rm s}$, *die Nullstelle $p_{\rm o} = -1/(RC) = -0.32 · 10^6 \cdot 1/{\rm s},$ *die beiden Pole $p_{\rm x1}$ und $p_{\rm x2}$ als Lösung der Gleichung :'"`UNIQ-MathJax16-QINU`"' :'"`UNIQ-MathJax17-QINU`"' In der obigen Grafik ist rechts das Pol–Nullstellen–Diagramm angegeben. *Die beiden Achsen bezeichnen den Real– und den Imaginärteil der Variablen $p$, jeweils normiert auf den Wert $10^6 · \rm 1/s\; (= 1/µs)$. *Man erkennt die Nullstelle bei $p_{\rm o} =\, –0.32$ als Kreis und die Polstellen bei $p_{\rm x1} = \,–0.4$ und $p_{\rm x2} = \,–1.6$ als Kreuze. <div style="clear:both;"> </div> </div> =='"`UNIQ--h-4--QINU`"'Eigenschaften der Pole und Nullstellen== <br> Die Übertragungsfunktion $H_{\rm L}(p)$ einer jeden realisierbaren Schaltung wird durch $Z$ Nullstellen und $N$ Pole zusammen mit einer Konstanten $K$ vollständig beschrieben, wobei folgende Einschränkungen gelten: *Es gilt stets $Z ≤ N$. Mit $Z > N$ wäre im Grenzfall für $p → ∞$ (also für sehr hohe Frequenzen) auch die $p$–Übertragungsfunktion "unendlich groß". *Die Nullstellen $p_{\rm oi}$ und die Pole $p_{ {\rm x}i}$ sind im allgemeinen komplex und weisen wie $p$ die Einheit $\rm 1/s$ auf. Gilt $Z < N$, so besitzt auch die Konstante $K$ eine Einheit. *Die Pole und Nullstellen können reell sein, wie im letzten Beispiel gezeigt. Sind sie komplex, so treten immer zwei konjugiert–komplexe Polstellen bzw. zwei konjugiert–komplexe Nullstellen auf, da $H_{\rm L}(p)$ stets eine reelle gebrochen–rationale Funktion darstellt. *Alle Pole liegen in der linken Halbebene oder auf der imaginären Achse (Grenzfall). Diese Eigenschaft ergibt sich aus der erforderlichen und vorausgesetzten Kausalität zusammen mit dem [[Linear_and_Time_Invariant_Systems/Laplace–Rücktransformation#Einige_Ergebnisse_der_Funktionentheorie|Hauptsatz der Funktionstheorie]], der im nächsten Kapitel angegeben wird. *Nullstellen können sowohl in der linken als auch in der rechten $p$–Halbebene auftreten oder auch auf der imaginären Achse. Ein Beispiel für Nullstellen in der rechten Halbebene findet man in der [[Aufgaben:3.4Z_Verschiedene_Allpässe|Aufgabe 3.4Z]], die sich mit Allpässen beschäftigt. *Bei den so genannten ''Minimum–Phasen–Systemen'' sind in der rechten $p$–Halbebene nicht nur Pole verboten, sondern auch Nullstellen. Der Realteil aller Singularitäten ist hier nie positiv. Diese Eigenschaften werden nun an drei Beispielen verdeutlicht. <div class="greybox"> $\text{Example 3:}$ Ausgehend von der bereits im letzten Abschnitt betrachteten [[Linear_and_Time_Invariant_Systems/Laplace–Transformation_und_p–Übertragungsfunktion#Pol.E2.80.93Nullstellen.E2.80.93Darstellung_von_Schaltungen|Vierpolschaltung]] $(L$ im Längszweig, $R$ und $C$ im Querzweig$)$ können die charakteristischen Größen der Übertragungsfunktion wie folgt angegeben werden: :'"`UNIQ-MathJax18-QINU`"' Die Grafik zeigt drei verschiedene Diagramme mit unterschiedlichen Kapazitätswerten $C$. Es gilt stets $R = 50 \ \rm Ω$ und $L = 25 \ \rm µ H$. Die Achsen sind auf die Variable $A = R/(2L) = 10^6 · \rm 1/s$ normiert, und der konstante Faktor ist jeweils $K = 2A = 2 · 10^6 · \rm 1/s.$ [[File:EN_LZI_T_3_2_S5_neu.png|center|frame|Lage der Nullstelle und der Pole für $Z = 1$ und $N = 2$|class=fit]] *Für $B < A$ erhält man '''zwei reelle Pole''' und eine Nullstelle rechts von $-A/2$. Für $C = 62.5 \ \rm nF$ ergibt sich (linkes Diagramm): :'"`UNIQ-MathJax19-QINU`"' *Für $B > A$ ergeben sich '''zwei konjugiert–komplexe Pole''' und eine Nullstelle links von $-A/2$. Für $C = 8 \ \rm nF$ (rechtes Diagramm): :'"`UNIQ-MathJax20-QINU`"' *Der Fall $A = B$ führt zu '''einer reellen doppelten Polstelle''' und einer Nullstelle bei $– A/2$. Für $C = 400 \ \rm nF$ (mittleres Diagramm): :'"`UNIQ-MathJax21-QINU`"' Die Impulsantworten $h(t)$ ergeben sich entsprechend dem folgenden Kapitel [[Linear_and_Time_Invariant_Systems/Laplace–Rücktransformation|Laplace–Rücktransformation]] wie folgt: *Bei der linken Konstellation ist $h(t)$ [[Linear_and_Time_Invariant_Systems/Laplace–Rücktransformation#Aperiodisch_abklingende_Impulsantwort|aperiodisch abklingend]]. *Bei der rechten Konstellation ist $h(t)$ [[Linear_and_Time_Invariant_Systems/Laplace–Rücktransformation#Ged.C3.A4mpft_oszillierende_Impulsantwort|gedämpft oszillierend]]. *Bei der mittleren Konstellation spricht man vom [[Linear_and_Time_Invariant_Systems/Laplace–Rücktransformation#Aperiodischer_Grenzfall|aperiodischen Grenzfall]]. <div style="clear:both;"> </div> </div> =='"`UNIQ--h-5--QINU`"'Grafische Ermittlung von Dämpfung und Phase== <br> Gegeben sei die $p$–Übertragungsfunktion in der Pol–Nullstellen–Notation: :'"`UNIQ-MathJax22-QINU`"' Zum herkömmlichen Frequenzgang $H(f)$ kommt man, indem man das Argument $p$ von $H_{\rm L}(p)$ durch ${\rm j} \cdot 2πf$ ersetzt: [[File:EN_LZI_T_3_2_S6.png|right|frame|Ausgangsdiagramm zur Berechnung <br>von Dämpfung und Phase|class=fit]] :'"`UNIQ-MathJax23-QINU`"' Wir betrachten nun eine feste Frequenz $f$ und beschreiben die Abstände und Winkel aller Nullstellen durch Vektoren: :'"`UNIQ-MathJax24-QINU`"' In gleicher Weise gehen wir für die Polstellen vor: :'"`UNIQ-MathJax25-QINU`"' Die Grafik zeigt die Beträge und Phasenwinkel für ein System *mit $Z = 2$ Nullstellen in der rechten Halbebene *und $N = 2$ Polstellen in der linken Halbebene. Zu berücksichtigen ist zudem die Konstante $K$. Mit dieser Vektordarstellung kann für den Frequenzgang geschrieben werden: :'"`UNIQ-MathJax26-QINU`"' Stellt man $H(f)$ durch die Dämpfungsfunktion $a(f)$ und die Phasenfunktion $b(f)$ nach der allgemein gültigen Beziehung $H(f) = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$ dar, so erhält man durch den Vergleich mit der obigen Gleichung das folgende Ergebnis: *Bei geeigneter Normierung aller dimensionsbehafteten Größen gilt für die Dämpfung in Neper $(1 \ \rm Np$ entspricht $8.686 \ \rm dB)$: :'"`UNIQ-MathJax27-QINU`"' *Die Phasenfunktion in Radian $\rm (rad)$ ergibt sich entsprechend der oberen Skizze zu :'"`UNIQ-MathJax28-QINU`"' [[File:P_ID1762__LZI_T_3_2_S6b_neu.png |right|frame| Zur Berechnung der Dämpfungs– und Phasenfunktion (Bildschirmabzug des Programms "Kausale Systeme & Laplace–Transformation" in einer früheren deutschen Version)|class=fit]] <div class="greybox"> $\text{Example 4:}$ Die Grafik verdeutlicht die Berechnung *der Dämpfungsfunktion $a(f)$ ⇒ roter Kurvenverlauf, und *der Phasenfunktion $b(f)$ ⇒ grüner Kurvenverlauf eines Vierpols, der durch den Faktor $K = 1.5$, eine Nullstelle bei $-3$ und zwei Pole bei $–1 \pm {\rm j} · 4$ festliegt. Die angegebenen Zahlenwerte gelten für die Frequenz $2πf = 3$: :'"`UNIQ-MathJax29-QINU`"' :'"`UNIQ-MathJax30-QINU`"' :'"`UNIQ-MathJax31-QINU`"' Die Herleitung dieser Zahlenwerte ist im umrahmten Block verdeutlicht. Für den Betragsfrequenzgang $\vert H(f)\vert$ ⇒ blauer Kurvenverlauf ergibt sich ein bandpassähnlicher Verlauf mit
- $$\vert H(f = 0)\vert \approx 0.25\hspace{0.05cm}, \hspace{0.5cm} \vert H(f = {4}/(2\pi)\vert \approx 0637\hspace{0.05cm},\hspace{0.5cm} \vert H(f \rightarrow \infty)\vert= 0 \hspace{0.05cm} .$$
Exercises for the chapter
Exercise 3.2: Laplace Transform
Exercise 3.2Z: Laplace and Fourier
Exercise 3.3: p-Transfer Function
Exercise 3.3Z: High- and Low-Pass Filters in p-Form
Exercise 3.4: Attenuation and Phase Response
Exercise 3.4Z: Various All-Pass Filters