Frequency Modulation (FM)

1 Instantaneous frequency
2 Signal characteristics with frequency modulation
3 Frequenzmodulation eines Cosinussignals
4 WM–Spektrum einer harmonischen Schwingung
5 Einfluss einer Bandbegrenzung bei Winkelmodulation
6 Realisierung eines FM–Modulators
7 PLL–Realisierung eines FM–Demodulators
8 Aufgaben zum Kapitel
9 Quellenverzeichnis

Instantaneous frequency

We will once again assume an angle-modulated signal:

$$s(t) = A_{\rm T} \cdot \cos \big[\psi(t)\big].$$

All the information about the source signal $q(t)$

is thus exclusively captured by the angular function $ψ(t)$ ,
while the envelope $a(t) = A_{\rm T}$ is constant.

$\text{Definitions:}$

The instantaneous frequency is the derivative of the angular function with respect to time:

$$\omega_{\rm A}(t) = \frac{ {\rm d}\psi(t)}{ {\rm d}t}\hspace{0.05cm}.$$

Accordingly, the instantaneous frequency is described by:

$$f_{\rm A}(t) = \frac{\omega_{\rm A}(t)}{2\pi} = \frac{1}{2\pi} \cdot \frac{ {\rm d}\hspace{0.03cm}\psi(t)}{ {\rm d}t}\hspace{0.05cm}.$$

The frequency deviation is the maximum deviation $Δf_{\rm A}$ of the time-dependent instantaneous frequency $f_{\rm A}(t)$ from the constant carrier frequency $f_{\rm T}$.

For an angle modulation with carrier frequency $f_{\rm T}$ , the instantaneous frequency oscillates in the range

$$f_{\rm T} - \Delta f_{\rm A} \le f_{\rm A}(t) \le f_{\rm T} + \Delta f_{\rm A}\hspace{0.05cm}.$$

It should be emphasized that there is a fundamental difference between the instantaneous frequency $f_{\rm A}(t)$ and the spectrum $S(f)$ of an angle-modulated signal $s(t)$ that can be measured with a spectrum analyzer, as illustrated by the following example.

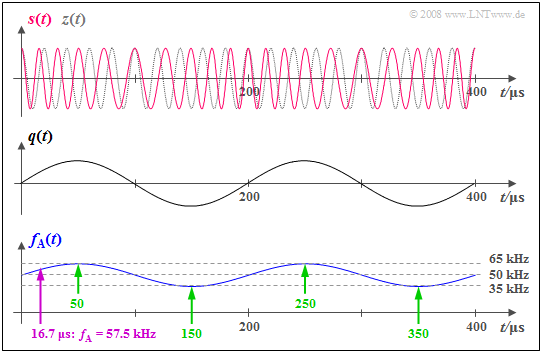
$\text{Example 1:}$ The graph shows the phase-modulated signal

$$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\psi(t)\big] = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[2 \pi f_{\rm T} \hspace{0.05cm}t + \eta \cdot \sin (2 \pi f_{\rm N} \hspace{0.05cm} t)\big]$$

as well as the instantaneous frequency plotted beneath

$$f_{\rm A}(t) = \frac{1}{2 \pi} \cdot \frac{ {\rm d}\hspace{0.03cm}\psi(t)}{ {\rm d}t} = f_{\rm T} + \Delta f_{\rm A}\cdot \cos (2 \pi f_{\rm N} \hspace{0.05cm} t) \hspace{0.05cm}.$$

Illustration of instantaneous frequency

Here, the system parameters are:

$f_{\rm T} = 50 \ \rm kHz$,
$f_{\rm N} = 5 \ \rm kHz$,
$η = 3$.

From this, we derive the frequency deviation

$Δf_{\rm A} = η · f_{\rm N} = 15 \ \rm kHz$.

In the middle, the qualitative progression of the sinusoidal source signal $q(t)$ is sketched for reference.
From these graphs, one can see:

The instantaneous frequency $f_{\rm A}(t)$ can take on arbitrary values between $f_{\rm T} + Δf_{\rm A} = 65 \ \rm kHz$ $($at $t = 50\ \rm µ s,\ 250 \ µ s$, etc.$)$ and $f_{\rm T} \ – Δf_{\rm A} = 35 \ \rm kHz$ $($at $t = 150\ \rm µ s, \ 350 \ µ s$, etc.$)$ (see green marks).
At time $t ≈ 16.7 \ \rm µ s$ , for example, $f_{\rm A}(t) = 57.5 \ \rm kHz$ holds (purple arrow).
In contrast, the spectral function $S(f)$ consists of discrete Bessel lines at the frequencies ... , $30,\ 35,\ 40,\ 45,\ \mathbf{50},\ 55,\ 60,\ 65,\ 70$, ... $($each in $\rm kHz)$.
There is no spectral line at $f = 57.5 \ \rm kHz$ , though there is one at $f = 70 \ \rm kHz$.
In contrast, at no time does $f_{\rm A}(t) = 70 \ \rm kHz$ hold.

$\text{Therefore:}$

The instantaneous frequency $f_{\rm A}(t)$ is thus not a physically measurable frequency in the conventional sense, but only an abstract mathematical quantity, namely the derivative of the angular function $ψ(t)$.

Signal characteristics with frequency modulation

As in the chapter Phase Modulation we will assume that the carrier signal $z(t)$ has a cosine waveform and the source signal $q(t)$ is peak-limited.

$\text{Definition:}$ In a communication system, if the instantaneous angular frequency $ω_{\rm A}(t)$ is linearly dependent on the instantaneous value of the source signal $q(t)$, we call this frequency modulation $\rm (FM)$:

$$\omega_{\rm A}(t) = 2 \pi \cdot f_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) \hspace{0.05cm}.$$

Here, $K_{\rm FM}$ denotes a dimensionally restricted constant. If $q(t)$ represents a voltage waveform, $K_{\rm FM}$ has the unit $\rm V^{–1}s^{–1}$.

In frequency modulation, the angular function $\psi(t)$ and the modulated signal $s(t)$ are given by:

$$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm FM} \cdot \int q(t)\hspace{0.1cm}{\rm d}t \hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s(t) = A_{\rm T} \cdot \cos \big[\psi(t)\big] \hspace{0.05cm}.$$

From this equation, we can immediately see:

Even in the case of frequency modulation, the equivalent low-pass signal moves on an arc because of the constant envelope ⇒ $a(t) = A_{\rm T}$ .
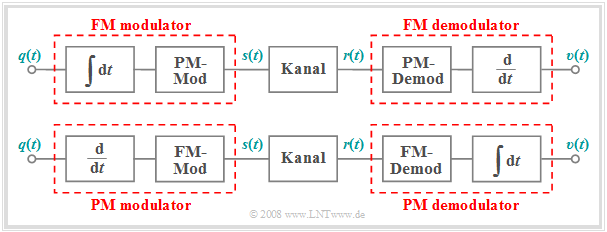
A frequency modulator can be implemented using an integrator and a phase modulator. Consequently, the FM demodulator consists of a PM demodulator and a differentiator, as shown in the upper part of the following diagram.

Relationship between phase and frequency modulation

The lower graph shows the inverse relationship ⇒ a possible description of a PM modulator and demodulator in terms of corresponding FM components.
It can also be seen from the above equation, that the earlier equation on page A very simple (though unfortunately not always correct) modulator equation in the first chapter of this book, will only hold for frequency modulation in very special cases.

Bei Frequenzmodulation ist die Umwandlung

$$s(t) = a(t) \cdot \cos (\omega (t) \cdot t + \phi(t)) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} s(t) = A_{\rm T} \cdot \cos (\omega (t) \cdot t + \phi_{\rm T})$$

nur manchmal erlaubt, zum Beispiel beim nichtlinearen digitalen Modulationsverfahren "Frequency Shift Keying" $\rm (FSK)$ mit rechteckförmigem Grundimpuls.

Frequenzmodulation eines Cosinussignals

Bei cosinusförmigem Quellensignal $q(t)$ und Frequenzmodulation gilt für die Augenblickskreisfrequenz:

$$q(t) = A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)\hspace{0.05cm}.$$

Integriert man diese über die Zeit, so erhält man die Winkelfunktion:

$$\psi(t) = \omega_{\rm T} \cdot t + \frac {K_{\rm FM} \cdot A_{\rm N}}{\omega_{\rm N}} \cdot \sin (\omega_{\rm N} \cdot t) \hspace{0.05cm}.$$

Ein Vergleich mit den Aussagen im Kapitel Phasenmodulation macht deutlich:

Die Frequenzmodulation eines Cosinussignals ergibt qualitativ das gleiche Sendesignal $s(t)$ wie die Phasenmodulation eines sinusförmigen Quellensignals $q(t)$.
Voraussetzung hierfür ist allerdings, dass die Modulatorkonstanten entsprechend dem Verhältnis $K_{\rm FM}/K_{\rm PM} = ω_{\rm N}$ aneinander angepasst sind.
Das Sendesignal $s(t)$ lässt sich somit bei den beiden Konstellationen „PM – Sinussignal” sowie „FM – Cosinussignal” einheitlich beschreiben:

$$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t)\big] \hspace{0.05cm}.$$

Allerdings sind bei Anwendung dieser Gleichung für den Modulationsindex $η$ bei Phasen– und Frequenzmodulation unterschiedliche Gleichungen zu verwenden:

$$\eta_{\rm PM} = {K_{\rm PM} \cdot A_{\rm N}},$$

$$\eta_{\rm FM} = \frac {K_{\rm FM} \cdot A_{\rm N}}{\omega_{\rm N}} \hspace{0.05cm}.$$

Ist das Quellensignal keine harmonische Schwingung, sondern setzt sich aus mehreren Frequenzen zusammen, so unterscheiden sich die Zeitsignale bei Phasen– und Frequenzmodulation auch qualitativ. Dies erkennt man beispielsweise beim früheren Vergleich von PSK und FSK.

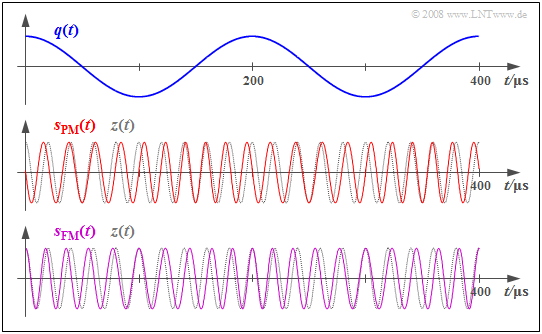
$\text{Beispiel 2:}$ Wir gehen nun von einem cosinusförmigen Quellensignal $q(t)$ mit der Amplitude $A_{\rm N} = 3 \ \rm V$ und der Frequenz $f_{\rm N} = 5 \ \rm kHz$ aus und betrachten die Signalverläufe von Phasenmodulation $\rm (PM)$ und Frequenzmodulation $\rm (FM)$ bei gleichem Modulationsindex $η = 1.5$.

$\rm (PM)$ und $\rm (FM)$ eines Cosinussignals mit $η = 1.5$

Die mittlere Grafik zeigt das phasenmodulierte Signal (rote Kurve) für die Modulatorparameter $f_{\rm T} = 50 \ \rm kHz$ und $K_{\rm PM} = \rm 0.5 V^{–1}$:

$$s_{\rm PM}(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \eta \cdot \cos (\omega_{\rm N} \cdot t)\big ] \hspace{0.05cm}.$$

Bei Phasenmodulation ergibt sich mit $A_{\rm N} = 3 \ \rm V$ für den Phasenhub (Modulationsindex) $η = 1.5 ≈ π/2$.
Die maximale Abweichung der Nulldurchgänge von ihren (äquidistanten) Solllagen beträgt somit etwa ein Viertel der Trägerperiode.
Ist das Quellensignal $q(t) > 0$, so kommen die Nulldurchgänge verfrüht, bei $q(t) < 0$ verspätet.

Die untere Grafik zeigt das frequenzmodulierte Signal mit gleichem Modulationsindex $η$:

$$s_{\rm FM}(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t)\big ] \hspace{0.05cm}.$$

Erreicht wird in diesem Fall $η = 1.5$ durch die Modulatorkonstante

$$K_{\rm FM} = \frac {\eta \cdot \omega_{\rm N} }{A_{\rm N} } = {K_{\rm PM} \cdot \omega_{\rm N} } $$

$$\Rightarrow \hspace{0.3cm} K_{\rm FM} = 0.5\,{\rm V}^{-1} \cdot 2 \pi \cdot 5\,{\rm kHz} = 15708\,{\rm V}^{-1}{\rm s}^{-1} \hspace{0.05cm}.$$

Der Frequenzhub beträgt hier $Δf_{\rm A} = η · f_{\rm N} = 7.5 \ \rm kHz$, und es treten Augenblicksfrequenzen zwischen $f_{\rm T}-Δf_{\rm A} = 42.5$ und $f_{\rm T}+Δf_{\rm A} =57.5 \ \rm kHz$ auf.
Die Nulldurchgänge stimmen nun bei den Maxima und den Minima des Quellensignals $q(t)$ mit denen des Trägersignals $z(t)$ überein, während die maximalen Phasenabweichungen bei den Nulldurchgängen von $q(t)$ zu erkennen sind. Dies ist genau umgekehrt wie bei der Phasenmodulation.

WM–Spektrum einer harmonischen Schwingung

Nun setzen wir für das Quellensignal allgemein eine harmonische Schwingung mit der Phase $ϕ_{\rm N}$ voraus:

$$q(t) = A_{\rm N} \cdot \cos \hspace{-0.1cm} \big[2 \pi f_{\rm N} \cdot t + \phi_{\rm N}\big ].$$

Uns interessiert die Spektralfunktion $S(f)$. Zur einfacheren Darstellung betrachten wir im Folgenden das Betragsspektrum $|S_+(f)|$ des analytischen Signals, aus dem $|S(f)|$ in der bekannten Weise hergeleitet werden kann.

Für jede Art von Winkelmodulation in der hier beschriebenen Weise – egal, ob Phasen– oder Frequenzmodulation – gilt unabhängig von der Phase $ϕ_{\rm N}$ des Quellensignals:

$$|S_{\rm +}(f)| = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}|{\rm J}_n (\eta)| \cdot \delta \big[f - (f_{\rm T} + n \cdot f_{\rm N})\big]\hspace{0.05cm}.$$

Diese Gleichung lässt sich wie folgt begründen:

Auf der Seite Äquivalentes TP-Signal bei PM wurde diese Gleichung für ein phasenmoduliertes Sinussignal abgeleitet, wobei $η = A_{\rm N} · K_{\rm PM}$ den Modulationsindex bezeichnet und ${\rm J}_n(η)$ die Besselfunkton erster Art und $n$–ter Ordnung. $K_{\rm PM}$ ist die Modulatorkonstante.
Durch eine andere Nachrichtenphase $ϕ_{\rm N}$ ändert sich nur die Phasenfunktion ${\rm arc} \ S_+(f)$, nicht aber das Betragsspektrum $|S_+(f)|$. Dieses wichtige Ergebnis wurde auch durch die Aufgabe 3.3Z bestätigt.
Auf der Seite Frequenzmodulation eines Cosinussignals wurde gezeigt, dass ein FM–Signal in gleicher Weise wie ein PM–Signal dargestellt werden kann, wenn der Modulationsindex $η = K_{\rm FM} · A_{\rm N}/ω_{\rm N}$ verwendet wird. Folgerichtig sind auch die Betragsspektren bei Phasen- und Frequenzmodulation in gleicher Form darstellbar.

Wir verweisen hier gerne auch auf den zweiten Teil des Lernvideos Winkelmodulation – Frequenz– und Phasenmodulation.

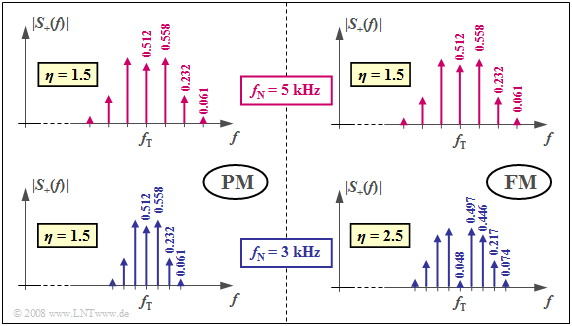
$\text{Beispiel 3:}$ Wir betrachten wieder eine harmonische Schwingung mit der Amplitude $A_{\rm N} = 3 \ \rm V$ nach

Diskrete Spektren bei Phasen– und Frequenzmodulation

einer Phasenmodulation mit $K_{\rm PM} = \rm 0.5 \ \rm V^{–1}$,
einer Frequenzmodulation mit $K_{\rm FM} = \rm 15708 \ \rm V^{–1}s^{–1}$.

Die zugehörigen Signalverläufe sind im $\text{Beispiel 2}$ dargestellt.

Bei beiden Übertragungssystemen ergibt sich für $f_{\rm N} = 5 \ \rm kHz$ ein Besselspektrum mit dem Modulationsindex $η = 1.5$.
Die identischen Betragsspektren des analytischen Signals (nur positive Frequenzen) sind in den beiden oberen Grafiken dargestellt.
Bessellinien mit Werten kleiner als $0.03$ sind hierbei in beiden Fällen vernachlässigt.

Die unteren Grafiken gelten für die Nachrichtenfrequenz $f_{\rm N} = 3 \ \rm kHz$:

Bei der Phasenmodulation ergibt sich gegenüber $f_{\rm N} = 5 \ \rm kHz$ nun eine schmalere Spektralfunktion, da der Abstand der Bessellinien nur mehr $3 \ \rm kHz$ beträgt (linke untere Grafik).
Da sich der Modulationsindex $η = 1.5$ nicht ändert, ergeben sich die gleichen Besselgewichte wie bei $f_{\rm N} = 5 \ \rm kHz$ (obere Grafik).
Auch bei der Frequenzmodulation treten nun die Bessellinien im Abstand von $3 \ \rm kHz$ auf (rechte untere Grafik).
Es gibt aber nun aufgrund des größeren Modulationsindex $η = 2.5$ deutlich mehr Bessellinien als im rechten oberen (für $η = 1.5$ gültigen) Diagramm.
Dies folgt aus der Tatsache, dass bei Frequenzmodulation $η$ umgekehrt proportional zu $f_{\rm N}$ ist.

Einfluss einer Bandbegrenzung bei Winkelmodulation

Fassen wir einige bisherige Resultate dieses Abschnittss kurz zusammen, wobei wir beispielhaft die Trägerfrequenz $f_{\rm T} = 100 \ \rm kHz$, die Nachrichtenfrequenz $f_{\rm N} = 5 \ \rm kHz$ und den Modulationsindex $η = π/2 \approx 1.5$ voraussetzen:

Das Spektrum einer winkelmodulierten Schwingung besteht aus Bessellinien um den Träger $f_{\rm T}$ im Abstand $f_{\rm N}$ der Nachrichtenfrequenz und ist theoretisch unendlich weit ausgedehnt.

Selbst wenn man alle Spektrallinien mit Beträgen kleiner als $0.01$ vernachlässigt, beträgt die dann endliche Bandbreite für $η = π/2$ noch immer $B_{\rm HF} = 8 · f_{\rm N} = 40 \ \rm kHz$.

Die Ortskurve – also der Verlauf des äquivalenten Tiefpass–Signals in der komplexen Ebene – ist im Idealfall ein Kreisbogen mit einem Öffnungswinkel von $±1.57 \ {\rm rad} = ±90^\circ$.

Dieser Kreisbogen nach der vektoriellen Addition ergibt sich allerdings nur dann, wenn alle Bessellinien in der Ortskurve mit den richtigen Zeigerlängen, den richtigen Phasenlagen und den richtigen Kreisfrequenzen rotieren.

Logischerweise wird die kreisbogenförmige Ortskurve verändert, wenn Spektrallinien verfälscht werden (zum Beispiel durch lineare Kanalverzerrungen) oder ganz fehlen (zum Beispiel durch eine Bandbegrenzung).

Da der ideale Winkeldemodulator die Phase $ϕ_r(t)$ des Empfangssignals detektiert und daraus das Sinkensignal $v(t)$ gewinnt, wird dieses dadurch verfälscht und zwar sogar nichtlinear. Das heißt: Die Verzerrungen sind irreversibel und können nicht durch ein lineares Filter kompensiert werden.

Das bedeutet gleichzeitig: Aufgrund linearer Verzerrungen auf dem Kanal kommt es zu nichtlinearen Verzerrungen im demodulierten Signal $v(t)$ ⇒ dadurch entstehen neue Frequenzen (Oberwellen), die im Quellensignal $q(t)$ nicht enthalten waren.

Je kleiner die zur Verfügung stehende Bandbreite $B_{\rm HF}$ ist und je größer der Modulationsindex $η$ gewählt wird, desto größer wird der die nichtlinearen Verzerrungen beschreibende Klirrfaktor $K$. Als Faustformel für die erforderliche HF–Bandbreite für einen geforderten Klirrfaktor $K$ gilt nach der so genannten "Carson–Regel":

$$K < 10\%\text{:}\hspace{0.6cm} B_{\rm HF} \ge 2 \cdot f_{\rm N} \cdot (\eta +1)\hspace{0.05cm},$$

$$K < 1\%\text{:}\hspace{0.72cm} B_{\rm HF} \ge 2 \cdot f_{\rm N} \cdot(\eta +2)\hspace{0.05cm}.$$

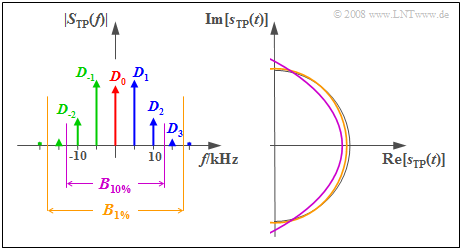
$\text{Beispiel 4:}$ Wir gehen weiterhin von den Systemparametern $f_{\rm T} = 100 \ \rm kHz$, $f_{\rm N} = 5 \ \rm kHz$ und $η = π/2$ aus. Die Grafik zeigt für diesen Fall links das Betragsspektrum $ \vert S_{\rm TP}(f) \vert$ des äquivalenten Tiefpass–Signals und rechts die zugehörige komplexe Zeitfunktion $s_{\rm TP}(t)$.

Einfluss einer Bandbegrenzung bei Winkelmodulation

Um den Klirrfaktor auf Werte $K < 1\%$ zu begrenzen, ist nach der Carson–Regel eine HF–Bandbreite von $B_{1 \%} ≈ 36 \ \rm kHz$ erforderlich.
Das äquivalente Tiefpass–Signal setzt sich dann aus der Konstanten $D_0$ und je drei entgegen dem Uhrzeigersinn $(D_1, D_2, D_3)$ bzw. im Uhrzeigersinn $(D_{-1}, D_{-2}, D_{-3})$ drehenden Zeigern zusammen:

$$\begin{align*}s_{\rm TP}(t) & = \sum_{n = - 3}^{+3}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.02cm}\cdot \hspace{0.05cm} t }\end{align*}$$

Die ockerfarbene Kurve in der Zeitbereichsdarstellung macht deutlich, dass sich das äquivalente Tiefpass-Signal durch diese Bandbegrenzung nur geringfügig vom verzerrungsfreien Halbkreis (dünne schwarze Linie) unterscheidet.

Gibt man sich mit einem Klirrfaktor $K < 10\%$ zufrieden, so ist bereits die HF–Bandbreite $B_{10 \%} ≈ 26\ \rm kHz$ ausreichend.

Damit werden auch die beiden Fourierkoeffizienten $D_3$ und $D_{-3}$ abgeschnitten und die violett dargestellte Ortskurve beschreibt einen Parabelabschnitt.
Die Simulation dieses Fallbeispiels liefert den Klirrfaktor $K ≈ 6\%$.
Man erkennt: Die Carson–Regel liefert oft ein etwas zu pessimistisches Ergebnis $(10\%$ anstelle von $6\%)$.

Realisierung eines FM–Modulators

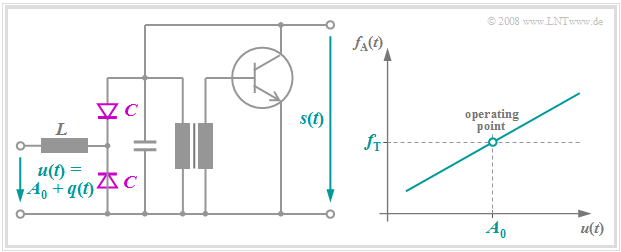
Eine Frequenzmodulation erhält man dann, wenn die Schwingfrequenz eines Oszillators im Rhythmus des modulierenden Signals verändert wird. Als frequenzbestimmende Elemente dienen meist RC–Glieder oder Schwingkreise. Die linke Grafik zeigt eine schaltungstechnische Realisierungsform; die genaue Schaltungsbeschreibung finden Sie in [Mäu 88]^[1]. Rechts ist die idealisierte Frequenz–Spannungskennlinie dargestellt.

Realisierung eines FM–Modulators und dessen Kennlinie

Hier sollen nur einige wenige Anmerkungen gemacht werden:

Die anliegende Spannung $u(t)$ setzt sich additiv aus dem Quellensignal $q(t)$ und einem Gleichanteil $A_0$ zusammen, der den Arbeitspunkt festlegt.
Die Kapazität $C$ der Kapazitätsdiode ist näherungsweise proportional zu $1/u^{2}(t)$, so dass sich die Schwingfrequenz des LC–Oszillators abhängig von $q(t)$ verändert.
Bei nur kleiner Frequenzänderung hängen $u(t)$ und $f_{\rm A}(t)$ linear zusammen. Damit ist die Augenblickskreisfrequenz mit der Steigung $K_{\rm FM}$ der Modulatorkennlinie wie folgt gegeben:

$$\omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) \hspace{0.05cm}.$$

Die Gegentaktschaltung aus den beiden Kapazitätsdioden dient unter Anderem zur Kompensation von Unsymmetrien und damit zur Verminderung der quadratischen Verzerrungen.
Mit dem Eingang $A_0+{\rm d}q(t)/{\rm d}t$ erhält man am Ausgang das frequenzmodulierte Signal $s(t)$.

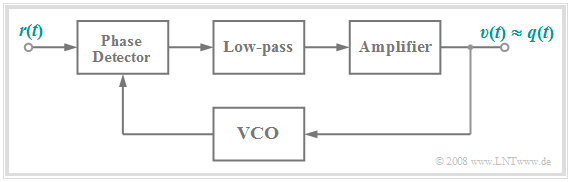
PLL–Realisierung eines FM–Demodulators

Die folgende Grafik zeigt eine zweite Realisierungsmöglichkeit des FM–Demodulators. Eine detaillierte Schaltungsbeschreibung dieses PLL–FM–Demodulators und weitere FM–Demodulatoren – zum Beispiel mittels Flankendiskriminator – finden Sie in [Mäu 88]^[1].

In Stichpunkten lässt sich diese Schaltung, die als Phasenregelschleife $($Phase–Locked–Loop, $\rm PLL)$ arbeitet, wie folgt beschreiben:

PLL – Realisierung eines FM–Demodulators

Der Phasendetektor ermittelt die Phasenunterschiede (Abstände der Nulldurchgänge) zwischen dem Empfangssignal $r(t)$ und dem vom VCO bereitgestellten Vergleichssignal.
Das Ausgangssignal $v(t)$ nach Tiefpass–Filterung und Verstärkung ist dann näherungsweise gleich dem Quellensignal $q(t)$, wenn dieses sendeseitig FM–moduliert wurde.
Das Ausgangssignal $v(t)$ wird gleichzeitig an den Eingang des spannungsgesteuerten Oszillators angelegt. Man bezeichnet diesen auch als Voltage Controlled Oscillator, abgekürzt $\rm VCO$.
Das Ausgangssignal des VCO wird permanent in der Weise nachgeregelt, dass dessen Frequenz möglichst der Augenblicksfrequenz $f_{\rm A}(t)$ des Empfangssignals $r(t)$ entspricht.