Structure of the Optimal Receiver

1 Block diagram and prerequisites
2 Fundamental approach to optimal receiver design
3 The theorem of irrelevance
4 Some properties of the AWGN channel
5 Beschreibung des AWGN-Kanals durch orthonormale Basisfunktionen
6 Optimaler Empfänger für den AWGN-Kanal
7 Implementierungsaspekte
8 Wahrscheinlichkeitsdichtefunktion der Empfangswerte
9 N–dimensionales Gaußsches Rauschen
10 Aufgaben zum Kapitel

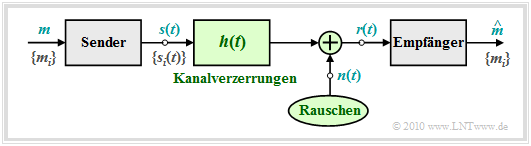
Block diagram and prerequisites

In this chapter, the structure of the optimal receiver of a digital transmission system is derived in very general terms, whereby

the modulation process and further system details are not specified further,
the basis functions and the signal space representation according to the chapter "Signals, Basis Functions and Vector Spaces" are assumed.

General block diagram of a communication system

To the above block diagram it is to be noted:

The symbol set size of the source is $M$ and the symbol set is $\{m_i\}$ with $i = 0$, ... , $M-1$. Let the corresponding symbol probabilities ${\rm Pr}(m = m_i)$ also be known to the receiver.

For message transmission $M$ different signal forms $s_i(t)$ are available; for the indexing variable the indexing $i = 0$, ... , $M-1$ shall be valid. There is a fixed relation between the messages $\{m_i\}$ and the signals $\{s_i(t)\}$. If $m =m_i$ is transmitted, the transmitted signal is $s(t) =s_i(t)$.

Linear channel distortions are taken into account in the above graph by the impulse response $h(t)$. In addition, a noise $n(t)$ (of some kind) is effective. With these two effects interfering with the transmission, the signal $r(t)$ arriving at the receiver can be given in the following way:

$$r(t) = s(t) \star h(t) + n(t) \hspace{0.05cm}.$$

The task of the (optimal) receiver is to find out, on the basis of its input signal $r(t)$, which of the $M$ possible messages $m_i$ – or which of the signals $s_i(t)$ – was sent. The estimated value for $m$ found by the receiver is characterized by a circumflex (French: Circonflexe) ⇒ $\hat{m}$.

$\text{Definition:}$ One speaks of an optimal receiver if the symbol error probability assumes the smallest possible value for the boundary conditions:

$$p_{\rm S} = {\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm minimum} \hspace{0.05cm}.$$

Notes:

In the following, we mostly assume the AWGN approach ⇒ $r(t) = s(t) + n(t)$, which means that $h(t) = \delta(t)$ is assumed to be distortion-free.
Otherwise, we can redefine the signals $s_i(t)$ as ${s_i}'(t) = s_i(t) \star h(t)$, i.e., impose the deterministic channel distortions on the transmitted signal.

Fundamental approach to optimal receiver design

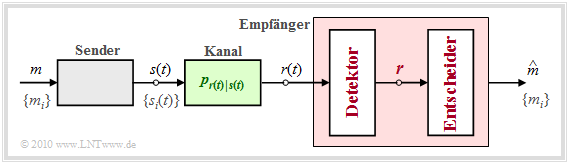
Compared to the "block diagram" shown on the previous page, we now perform some essential generalizations:

The transmission channel is described by the "conditional probability density function" $p_{\hspace{0.02cm}r(t)\hspace{0.02cm} \vert \hspace{0.02cm}s(t)}$ which determines the dependence of the received signal $r(t)$ on the transmitted signal $s(t)$.

If a certain signal $r(t) = \rho(t)$ has been received, the receiver has the task to determine the probability density functions based on this signal realization $\rho(t)$ and the $M$ conditional probability density functions

$$p_{\hspace{0.05cm}r(t) \hspace{0.05cm} \vert \hspace{0.05cm} s(t) } (\rho(t) \hspace{0.05cm} \vert \hspace{0.05cm} s_i(t))\hspace{0.2cm}{\rm with}\hspace{0.2cm} i = 0, \text{...} \hspace{0.05cm}, M-1$$

taking into account all possible transmitted signals $s_i(t)$ and their probabilities of occurrence ${\rm Pr}(m = m_i)$, find out which of the possible messages $m_i$ or which of the possible signals $s_i(t)$ was most likely transmitted.

Thus, the estimate of the optimal receiver is determined in general by the equation

$$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} p_{\hspace{0.02cm}s(t) \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( s_i(t) \hspace{0.05cm} \vert \hspace{0.05cm} \rho(t)) = {\rm arg} \max_i \hspace{0.1cm} p_{m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( \hspace{0.05cm}m_i\hspace{0.05cm} \vert \hspace{0.05cm}\rho(t))\hspace{0.05cm},$$

where it is considered that the transmitted message $m = m_i$ and the transmitted signal $s(t) = s_i(t)$ can be uniquely transformed into each other.

$\text{In other words:}$ The optimal receiver considers as the most likely transmitted message $m_i$ whose conditional probability density function $p_{\hspace{0.02cm}m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) }$ takes the largest possible value for the applied received signal $\rho(t)$ and under the assumption $m =m_i$.

Before we discuss the above decision rule in more detail, the optimal receiver should still be divided into two functional blocks according to the diagram:

Model for deriving the optimal receiver

The detector takes various measurements on the received signal $r(t)$ and summarizes them in the vector $\boldsymbol{r}$. With $K$ measurements $\boldsymbol{r}$ corresponds to a point in the $K$–dimensional vector space.

The decision forms the estimated value depending on this vector. For a given vector $\boldsymbol{r} = \boldsymbol{\rho}$ the decision rule is:

$$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) \hspace{0.05cm}.$$

In contrast to the upper decision rule, a conditional probability $P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} }$ now occurs instead of the conditional probability density function (PDF) $p_{m\hspace{0.05cm} \vert \hspace{0.05cm}r(t)}$. Please note the upper and lower case for the different meanings.

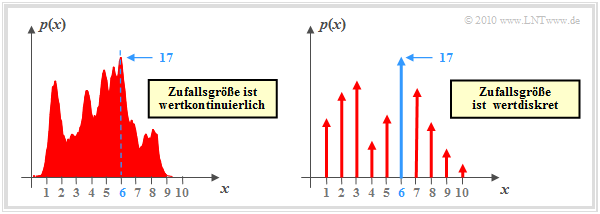
$\text{Example 1:}$ We now consider the function $y = {\rm arg}\hspace{0.05cm} \max \ p(x)$, where $p(x)$ describes the probability density function (PDF) of a continuous-valued or discrete-valued random variable $x$. In the second case (right graph), the PDF consists of a sum of Dirac functions with the probabilities as pulse weights.

Illustration of the "arg max" function

The graphic shows exemplary functions. In both cases the PDF maximum $(17)$ is at $x = 6$:

$$\max_i \hspace{0.1cm} p(x) = 17\hspace{0.05cm},$$

$$y = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} p(x) = 6\hspace{0.05cm}.$$

The (conditional) probabilities in the equation

$$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho})$$

are a posteriori probabilities.

"Bayes' theorem" can be used to write for this:

$$P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) = \frac{ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )}{p_{\boldsymbol{ r} } (\boldsymbol{\rho})} \hspace{0.05cm}.$$

The denominator term is the same for all alternatives $m_i$ and need not be considered for the decision. This gives the following rules:

$\text{Theorem:}$ The decision rule of the optimal receiver, also known as MAP receiver (stands for maximum–a–posteriori), is:

$$\hat{m}_{\rm MAP} = {\rm \hspace{0.05cm} arg} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}) = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm} m_i )\big ]\hspace{0.05cm}.$$

The advantage of this equation is that the conditional PDF $p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m }$ ("output under the condition input") describing the forward direction of the channel can be used. In contrast, the first equation uses the inference probabilities $P_{\hspace{0.05cm}m\hspace{0.05cm} \vert \hspace{0.02cm} \boldsymbol{ r} } $ ("input under the condition output").

$\text{Theorem:}$ A maximum likelihood receiver (ML receiver in short) uses the decision rule

$$\hat{m}_{\rm ML} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$

In this case, the possibly different occurrence probabilities ${\rm Pr}(m = m_i)$ are not used for the decision process, for example, because they are not known to the receiver.

See the earlier chapter "Optimal Receiver Strategies" for other derivations for these receiver types.

$\text{Conclusion:}$ For equally likely messages $\{m_i\}$ ⇒ ${\rm Pr}(m = m_i) = 1/M$, the generally slightly worse ML receiver is equivalent to the MAP receiver:

$$\hat{m}_{\rm MAP} = \hat{m}_{\rm ML} =\hspace{-0.1cm} {\rm\hspace{0.05cm} arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$

The theorem of irrelevance

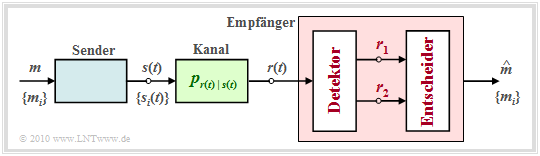
Note that the receiver described in the last section is optimal only if the detector is implemented in the best possible way, i.e., if no information is lost by the transition from the continuous signal $r(t)$ to the vector $\boldsymbol{r}$.

About the theorem of irrelevance

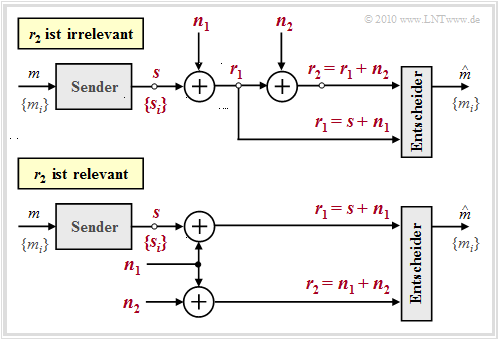
To clarify the question which and how many measurements have to be performed on the received signal $r(t)$ to guarantee optimality, the theorem of irrelevance is helpful. For this purpose, we consider the sketched receiver whose detector derives the two vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$ from the received signal $r(t)$ and makes them available to the decision. These quantities are related to the message $ m \in \{m_i\}$ via the composite probability density $p_{\boldsymbol{ r}_1, \hspace{0.05cm}\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}m }$.

The decision rule of the MAP receiver with adaptation to this example is:

$$\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 , \hspace{0.05cm}\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1, \hspace{0.05cm}\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) \big]= {\rm arg} \max_i \hspace{0.1cm}\big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )\big] \hspace{0.05cm}.$$

Here it is to be noted:

The vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$ are random variables. Their realizations are denoted here and in the following by $\boldsymbol{\rho}_1$ and $\boldsymbol{\rho}_2$. For emphasis, all vectors are shown in red in the graph.

The requirements for the application of the "theorem of irrelevance" are the same as those for a first order "Markov chain". The random variables $x$, $y$, $z$ then form a first order Markov chain if the distribution of $z$ is independent of $x$&nbsp for a given $y$. The first order Markov chain is the following:

$$p(x, y, z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}y) \hspace{0.25cm} {\rm instead \hspace{0.15cm}of} \hspace{0.25cm}p(x, y, z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}x, y) \hspace{0.05cm}.$$

In the general case, the optimal receiver must evaluate both vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$, since both composite probability densities $p_{\boldsymbol{ r}_1\hspace{0.05cm} \vert \hspace{0.05cm}m }$ and $p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1, \hspace{0.05cm}m }$ occur in the above decision rule.

In contrast, the receiver can neglect the second measurement without loss of information if $\boldsymbol{r}_2$ is independent of message $m$ for given $\boldsymbol{r}_1$:

$$p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 ) \hspace{0.05cm}.$$

In this case, the decision rule can be further simplified:

$$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) \big]$$

$$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 )\big]$$

$$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \big]\hspace{0.05cm}.$$

$\text{Example 2:}$ We consider two different system configurations with two noise terms $\boldsymbol{ n}_1$ and $\boldsymbol{ n}_2$ each to illustrate the theorem of irrelevance just presented. In the diagram all vectorial quantities are drawn in red. Moreover, the quantities $\boldsymbol{s}$, $\boldsymbol{ n}_1$ and $\boldsymbol{ n}_2$ are independent of each other.

Two examples of the theorem of irrelevance

The analysis of these two arrangements yields the following results:

In both cases, the decision must consider the component $\boldsymbol{ r}_1= \boldsymbol{ s}_i + \boldsymbol{ n}_1$, since only this component provides the information about the useful signal $\boldsymbol{ s}_i$ and thus about the transmitted message $m_i$.

In the upper configuration, $\boldsymbol{ r}_2$ contains no information about $m_i$ that has not already been provided by $\boldsymbol{ r}_1$. Rather, $\boldsymbol{ r}_2= \boldsymbol{ r}_1 + \boldsymbol{ n}_2$ is just a noisy version of $\boldsymbol{ r}_1$ and depends only on the noise $\boldsymbol{ n}_2$ once $\boldsymbol{ r}_1$ is known ⇒ $\boldsymbol{ r}_2$ is irrelevant:

$$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}_1 )= p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2 - \boldsymbol{\rho}_1 )\hspace{0.05cm}.$$

In the lower configuration, on the other hand, $\boldsymbol{ r}_2= \boldsymbol{ n}_1 + \boldsymbol{ n}_2$ is helpful to the receiver, since it provides it with an estimate of the noise term $\boldsymbol{ n}_1$ ⇒ $\boldsymbol{ r}_2$ should therefore not be discarded here. Formally, this result can be expressed as follows:

$$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) = p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i)= p_{\boldsymbol{ n}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i) = p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i ) \hspace{0.05cm}.$$

Since the message $\boldsymbol{ s}_i$ now appears in the argument of this function, $\boldsymbol{ r}_2$ is "not irrelevant" but quite relevant.

Some properties of the AWGN channel

In order to make further statements about the nature of the optimal measurements of the vector $\boldsymbol{ r}$, it is necessary to further specify the (conditional) probability density function $p_{\hspace{0.02cm}r(t)\hspace{0.05cm} \vert \hspace{0.05cm}s(t)}$ characterizing the channel. In the following, we will consider communication over the "AWGN channel", whose most important properties are briefly summarized again here:

The output signal of the AWGN channel is $r(t) = s(t)+n(t)$, where $s(t)$ indicates the transmitted signal and $n(t)$ is represented by a Gaussian noise process.

A random process $\{n(t)\}$ is said to be Gaussian if the elements of the $k$–dimensional random variables $\{n_1(t)\hspace{0.05cm} \text{...} \hspace{0.05cm}n_k(t)\}$ are jointly Gaussian ⇒ "Jointly Gaussian".

The average value of the AWGN noise is ${\rm E}\big[n(t)\big] = 0$. Moreover, $n(t)$ is "white", which means that the "power-spectral density" (PSD) is constant for all frequencies $($from $-\infty$ to $+\infty)$:

$${\it \Phi}_n(f) = {N_0}/{2} \hspace{0.05cm}.$$

According to the "Wiener-Chintchine theorem", the auto-correlation function (ACF) is obtained as the "Fourier retransform" of ${\it \Phi_n(f)}$:

$${\varphi_n(\tau)} = {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = {N_0}/{2} \cdot \delta(t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = \left\{ \begin{array}{c} \rightarrow \infty \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{or}} \hspace{0.15cm} \tau = 0 \hspace{0.05cm}, \\ {\rm f{or}} \hspace{0.15cm} \tau \ne 0 \hspace{0.05cm},\\ \end{array}$$

$N_0$ gibt dabei die physikalische (nur für $f \ge 0$ definierte) Rauschleistungsdichte an. Der konstante LDS–Wert $(N_0/2)$ und das Gewicht der Diracfunktion in der AKF $($ebenfalls $N_0/2)$ ergibt sich allein durch die zweiseitige Betrachtungsweise.

Weitere Informationen zu diesem Thema liefert das Lernvideo Der AWGN-Kanal im zweiten Teil.

Beschreibung des AWGN-Kanals durch orthonormale Basisfunktionen

Aus dem vorletzten Statement auf der letzten Seite geht hervor, dass

reines AWGN–Rauschen $n(t)$ stets eine unendliche Varianz (Leistung) aufweist: $\sigma_n^2 \to \infty$,
in der Realität demzufolge nur gefiltertes Rauschen $n\hspace{0.05cm}'(t) = n(t) \star h_n(t)$ auftreten kann.

Mit der Impulsantwort $h_n(t)$ und dem Frequenzgang $H_n(f) = {\rm F}\big [h_n(t)\big ]$ gelten dann folgende Gleichungen:

$${\rm E}\big[n\hspace{0.05cm}'(t) \big] \hspace{0.15cm} = \hspace{0.2cm} {\rm E}\big[n(t) \big] = 0 \hspace{0.05cm},$$

$${\it \Phi_{n\hspace{0.05cm}'}(f)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2} \cdot |H_{n}(f)|^2 \hspace{0.05cm},$$

$$ {\it \varphi_{n\hspace{0.05cm}'}(\tau)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2}\hspace{0.1cm} \cdot \big [h_{n}(\tau) \star h_{n}(-\tau)\big ]\hspace{0.05cm},$$

$$\sigma_n^2 \hspace{0.1cm} = \hspace{0.1cm} { \varphi_{n\hspace{0.05cm}'}(\tau = 0)} = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}h_n^2(t)\,{\rm d} t ={N_0}/{2}\hspace{0.1cm} \cdot < \hspace{-0.1cm}h_n(t), \hspace{0.1cm} h_n(t) \hspace{-0.05cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}{\it \Phi}_{n\hspace{0.05cm}'}(f)\,{\rm d} f = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|H_n(f)|^2\,{\rm d} f \hspace{0.05cm}.$$

Im Folgenden beinhaltet $n(t)$ stets implizit eine Bandbegrenzung; auf die Schreibweise $n'(t)$ wird also zukünftig verzichtet.

$\text{Bitte beachten Sie:}$ Ähnlich wie das Sendesignal $s(t)$ lässt sich auch der Rauschprozess $\{n(t)\}$ als gewichtete Summe von orthonormalen Basisfunktionen $\varphi_j(t)$ schreiben.

Im Gegensatz zu $s(t)$ ist allerdings nun eine Beschränkung auf eine endliche Anzahl an Basisfunktionen nicht möglich.
Vielmehr gilt bei rein stochastischen Größen für die entsprechende Signaldarstellung stets

$$n(t) = \lim_{N \rightarrow \infty} \sum\limits_{j = 1}^{N}n_j \cdot \varphi_j(t) \hspace{0.05cm},$$

wobei der Koeffizient $n_j$ durch die Projektion von $n(t)$ auf die Basisfunktion $\varphi_j(t)$ bestimmt ist:

$$n_j = \hspace{0.1cm} < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.05cm}.$$

Hinweis: Um eine Verwechslung mit den Basisfunktionen $\varphi_j(t)$ zu vermeiden, wird im Folgenden die AKF $\varphi_n(\tau)$ des Rauschprozesses stets nur noch als der Erwartungswert ${\rm E}\big [n(t) \cdot n(t + \tau)\big ]$ ausgedrückt.

Optimaler Empfänger für den AWGN-Kanal

Optimaler Empfänger beim AWGN-Kanal

Auch das Empfangssignal $r(t) = s(t) + n(t)$ lässt sich in bekannter Weise in Basisfunktionen zerlegen:

$$r(t) = \sum\limits_{j = 1}^{\infty}r_j \cdot \varphi_j(t) \hspace{0.05cm}.$$

Zu berücksichtigen ist:

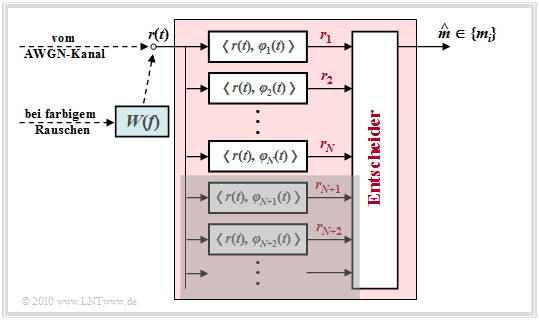
Die $M$ möglichen Sendesignale $\{s_i(t)\}$ spannen einen Signalraum mit insgesamt $N$ Basisfunktionen $\varphi_1(t)$, ... , $\varphi_N(t)$ auf.

Diese $N$ Basisfunktionen $\varphi_j(t)$ werden gleichzeitig zur Beschreibung des Rauschsignals $n(t)$ und des Empfangssignals $r(t)$ verwendet.

Zur vollständigen Charakterisierung von $n(t)$ bzw. $r(t)$ werden nun aber darüber hinaus noch unendlich viele weitere Basisfunktionen $\varphi_{N+1}(t)$, $\varphi_{N+2}(t)$, ... benötigt.

Damit ergeben sich die Koeffizienten des Empfangssignals $r(t)$ gemäß folgender Gleichung, wobei berücksichtigt ist, dass die Signale $s_i(t)$ und das Rauschen $n(t)$ voneinander unabhängig sind:

$$r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}=\hspace{0.1cm} \left\{ \begin{array}{c} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > + < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}= s_{ij}+ n_j\\ < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm} = n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm} \hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$

Somit ergibt sich für den optimalen Empfänger die oben skizzierte Struktur.

Betrachten wir zunächst den AWGN–Kanal. Hier kann auf das Vorfilter mit dem Frequenzgang $W(f)$ verzichtet werden, das für farbiges Rauschen vorgesehen ist.

Der Detektor des optimalen Empfängers bildet die Koeffizienten $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t)\hspace{-0.05cm} >$ und reicht diese an den Entscheider weiter. Basiert die Entscheidung auf sämtlichen – also unendlich vielen – Koeffizienten $r_j$, so ist die Wahrscheinlichkeit für eine Fehlentscheidung minimal und der Empfänger optimal.

Die reellwertigen Koeffizienten $r_j$ wurden oben wie folgt berechnet:

$$r_j = \left\{ \begin{array}{c} s_{ij} + n_j\\ n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$

Nach dem Theorem der Irrelevanz lässt sich zeigen, dass für additives weißes Gaußsches Rauschen

die Optimalität nicht herabgesetzt wird, wenn man die nicht von der Nachricht $(s_{ij})$ abhängigen Koeffizienten $r_{N+1}$, $r_{N+2}$, ... nicht in den Entscheidungsprozess einbindet, und somit

der Detektor nur die Projektionen des Empfangssignals $r(t)$ auf die $N$ durch das Nutzsignal $s(t)$ vorgegebenen Basisfunktionen $\varphi_{1}(t)$, ... , $\varphi_{N}(t)$ bilden muss.

In der Grafik ist diese signifikante Vereinfachung durch die graue Hinterlegung angedeutet.

Im Fall von farbigem Rauschen ⇒ Leistungsdichtespektrum ${\it \Phi}_n(f) \ne {\rm const.}$ ist lediglich zusätzlich ein Vorfilter mit dem Amplitudengang $|W(f)| = {1}/{\sqrt{\it \Phi}_n(f)}$ erforderlich. Man nennt dieses Filter auch "Whitening Filter", da die Rauschleistungsdichte am Ausgang wieder konstant – also "weiß" – ist.

Genaueres hierzu finden Sie im Kapitel Matched-Filter bei farbigen Störungen des Buches "Stochastische Signaltheorie".

Implementierungsaspekte

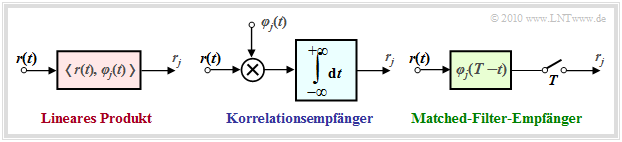
Wesentliche Bestandteile des optimalen Empfängers sind die Berechnungen der inneren Produkte gemäß den Gleichungen $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} >$. Diese können auf verschiedene Art und Weise implementiert werden:

Beim Korrelationsempfänger (Näheres zu dieser Implementierung finden Sie im gleichnamigen Kapitel) werden die inneren Produkte direkt entsprechend der Definition mit analogen Multiplizierern und Integratoren realisiert:

$$r_j = \int_{-\infty}^{+\infty}r(t) \cdot \varphi_j(t) \,{\rm d} t \hspace{0.05cm}.$$

Der Matched–Filter–Empfänger, der bereits im Kapitel Optimaler Binärempfänger zu Beginn dieses Buches hergeleitet wurde, erzielt mit einem linearen Filter mit der Impulsantwort $h_j(t) = \varphi_j(t) \cdot (T-t)$ und anschließender Abtastung zum Zeitpunkt $t = T$ das gleiche Ergebnis:

$$r_j = \int_{-\infty}^{+\infty}r(\tau) \cdot h_j(t-\tau) \,{\rm d} \tau = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(T-t+\tau) \,{\rm d} \tau \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_j (t = \tau) = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(\tau) \,{\rm d} \tau = r_j \hspace{0.05cm}.$$

Die Abbildung zeigt die beiden möglichen Realisierungsformen des optimalen Detektors.

Drei unterschiedliche Implementierungen des inneren Produktes

Wahrscheinlichkeitsdichtefunktion der Empfangswerte

Bevor wir uns im folgenden Kapitel der optimalen Gestaltung des Entscheiders und der Berechnung und Annäherung der Fehlerwahrscheinlichkeit zuwenden, erfolgt zunächst eine für den AWGN–Kanal gültige statistische Analyse der Entscheidungsgrößen $r_j$.

Signalraumkonstellation und WDF des Empfangssignals

Dazu betrachten wir nochmals den optimalen Binärempfänger für die bipolare Basisbandübertragung über den AWGN–Kanal, wobei wir von der für das vierte Hauptkapitel gültigen Beschreibungsform ausgehen.

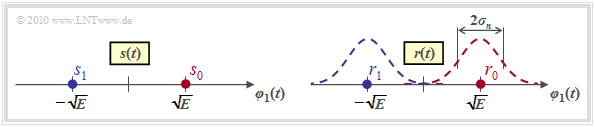
Mit den Parametern $N = 1$ und $M = 2$ ergibt sich für das Sendesignal die in der linken Grafik dargestellte Signalraumkonstellation

mit nur einer Basisfunktion $\varphi_1(t)$, wegen $N = 1$,
mit den beiden Signalraumpunkten $s_i \in \{s_0, \hspace{0.05cm}s_1\}$, wegen $M = 2$.

Für das Signal $r(t) = s(t) + n(t)$ am Ausgang des AWGN–Kanals ergibt sich im rauschfreien Fall ⇒ $r(t) = s(t)$ die genau gleiche Konstellation. Die Signalraumpunkte liegen somit bei

$$r_0 = s_0 = \sqrt{E}\hspace{0.05cm},\hspace{0.2cm}r_1 = s_1 = -\sqrt{E}\hspace{0.05cm}.$$

Bei Berücksichtigung des (bandbegrenzten) AWGN–Rauschens $n(t)$ überlagern sich den beiden Punkten $r_0$ und $r_1$ jeweils Gaußkurven mit der Varianz $\sigma_n^2$ ⇒ Streuung $\sigma_n$ (siehe rechte Grafik). Die WDF der Rauschkomponente $n(t)$ lautet dabei:

$$p_n(n) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {n^2}/(2 \sigma_n^2)}\hspace{0.05cm}.$$

Für die bedingte Wahrscheinlichkeitsdichte, dass der Empfangswert $\rho$ anliegt, wenn $s_i$ gesendet wurde, ergibt sich dann folgender Ausdruck:

$$p_{\hspace{0.02cm}r\hspace{0.05cm}|\hspace{0.05cm}s}(\rho\hspace{0.05cm}|\hspace{0.05cm}s_i) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {(\rho - s_i)^2}/(2 \sigma_n^2)} \hspace{0.05cm}.$$

Zu den Einheiten der hier aufgeführten Größen ist zu bemerken:

$r_0 = s_0$ und $r_1 = s_1$ sowie $n$ sind jeweils Skalare mit der Einheit "Wurzel aus Energie".

Damit ist offensichtlich, dass $\sigma_n$ ebenfalls die Einheit "Wurzel aus Energie" besitzt und $\sigma_n^2$ eine Energie darstellt.

Beim AWGN–Kanal ist die Rauschvarianz $\sigma_n^2 = N_0/2$. Diese ist also ebenfalls eine physikalische Größe mit der Einheit $\rm W/Hz = Ws$.

Die hier angesprochene Thematik wird in der Aufgabe 4.6 an Beispielen verdeutlicht.

N–dimensionales Gaußsches Rauschen

Liegt ein $N$–dimensionales Modulationsverfahren vor, das heißt, es gilt mit $0 \le i \le M-1$ und $1 \le j \le N$:

$$s_i(t) = \sum\limits_{j = 1}^{N} s_{ij} \cdot \varphi_j(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + \hspace{0.05cm}\text{...}\hspace{0.05cm} + s_{iN} \cdot \varphi_N(t)\hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \boldsymbol{ s}_i = \left(s_{i1}, s_{i2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, s_{iN}\right ) \hspace{0.05cm},$$

so muss der Rauschvektor $\boldsymbol{ n}$ ebenfalls mit der Dimension $N$ angesetzt werden. Das gleiche gilt auch für den Empfangsvektor $\boldsymbol{ r}$:

$$\boldsymbol{ n} = \left(n_{1}, n_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, n_{N}\right ) \hspace{0.01cm},\hspace{0.2cm}\boldsymbol{ r} = \left(r_{1}, r_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, r_{N}\right )\hspace{0.05cm}.$$

Die Wahrscheinlichkeitsdichtefunktion (WDF) lautet dann für den AWGN–Kanal mit der Realisierung $\boldsymbol{ \eta}$ des Rauschsignals

$$p_{\boldsymbol{ n}}(\boldsymbol{ \eta}) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^N } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \eta} ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm},$$

und für die bedingte WDF in der Maximum–Likelihood–Entscheidungsregel ist anzusetzen:

$$p_{\hspace{0.02cm}\boldsymbol{ r}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_i) \hspace{-0.1cm} = \hspace{0.1cm} p_{\hspace{0.02cm} \boldsymbol{ n}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} - \boldsymbol{ s}_i \hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}_i) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \rho} - \boldsymbol{ s}_i ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.$$

Die Gleichung ergibt sich aus der allgemeinen Darstellung der $N$–dimensionalen Gaußschen WDF im Abschnitt Korrelationsmatrix des Buches "Stochastische Signaltheorie" unter der Voraussetzung, dass die Komponenten unkorreliert (und somit statistisch unabhängig) sind. $||\boldsymbol{ \eta}||$ bezeichnet man als die Norm (Länge) des Vektors $\boldsymbol{ \eta}$.

Zweidimensionale Gauß–WDF

$\text{Beispiel 3:}$ Rechts dargestellt ist die zweidimensionale Gauß–WDF $p_{\boldsymbol{ n} } (\boldsymbol{ \eta})$ der 2D–Zufallsgröße $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$. Beliebige Realisierungen der Zufallsgröße $\boldsymbol{ n}$ werden mit $\boldsymbol{ \eta} = (\eta_1,\hspace{0.05cm}\eta_2)$ bezeichnet.

Die Gleichung der dargestellten Glockenkurve lautet:

$$p_{n_1, n_2}(\eta_1, \eta_2) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{ \eta_1^2 + \eta_2^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}. $$

Das Maximum dieser Funktion liegt bei $\eta_1 = \eta_2 = 0$ und hat den Wert $2\pi \cdot \sigma_n^2$.
Mit $\sigma_n^2 = N_0/2$ lässt sich die 2D–WDF in Vektorform auch wie folgt schreiben:

$$p_{\boldsymbol{ n} }(\boldsymbol{ \eta}) = \frac{1}{\pi \cdot N_0 } \cdot {\rm exp} \left [ - \frac{\vert \vert \boldsymbol{ \eta} \vert \vert ^2}{N_0}\right ]\hspace{0.05cm}.$$

Diese rotationssymmetrische WDF eignet sich zum Beispiel für die Beschreibung/Untersuchung eines zweidimensionalen Modulationsverfahrens wie M–QAM, M–PSK oder 2–FSK.

Oft werden zweidimensionale reelle Zufallsgrößen aber auch eindimensional–komplex dargestellt, meist in der Form $n(t) = n_{\rm I}(t) + {\rm j} \cdot n_{\rm Q}(t)$. Die beiden Komponenten bezeichnet man dann als Inphaseanteil $n_{\rm I}(t)$ und Quadraturanteil $n_{\rm Q}(t)$ des Rauschens.

Die Wahrscheinlichkeitsdichtefunktion hängt nur vom Betrag $\vert n(t) \vert$ der Rauschvariablen ab und nicht von Winkel ${\rm arc} \ n(t)$. Das heißt: Komplexes Rauschen ist zirkulär symmetrisch (siehe Grafik).

Zirkulär symmetrisch bedeutet auch, dass die Inphasekomponente $n_{\rm I}(t)$ und die Quadraturkomponente $n_{\rm Q}(t)$ die gleiche Verteilung aufweisen und damit auch gleiche Varianz (Streuung) besitzen:

$$ {\rm E} \big [ n_{\rm I}^2(t)\big ] = {\rm E}\big [ n_{\rm Q}^2(t) \big ] = \sigma_n^2 \hspace{0.05cm},\hspace{1cm}{\rm E}\big [ n(t) \cdot n^*(t) \big ]\hspace{0.1cm} = \hspace{0.1cm} {\rm E}\big [ n_{\rm I}^2(t) \big ] + {\rm E}\big [ n_{\rm Q}^2(t)\big ] = 2\sigma_n^2 \hspace{0.05cm}.$$

Abschließend noch einige Bezeichnungsvarianten für Gaußsche Zufallsgrößen:

$$x ={\cal N}(\mu, \sigma^2) \hspace{-0.1cm}: \hspace{0.3cm}\text{reelle gaußverteilte Zufallsgröße, mit Mittelwert}\hspace{0.1cm}\mu \text { und Varianz}\hspace{0.15cm}\sigma^2 \hspace{0.05cm},$$

$$y={\cal CN}(\mu, \sigma^2)\hspace{-0.1cm}: \hspace{0.12cm}\text{komplexe gaußverteilte Zufallsgröße} \hspace{0.05cm}.$$

Aufgaben zum Kapitel

Aufgabe 4.4: Maximum–a–posteriori und Maximum–Likelihood

Aufgabe 4.5: Theorem der Irrelevanz