Conclusions from the Allocation Theorem

1. Linear and Time Invariant Systems
2. Description of Causal Realizable Systems
3. Conclusions from the Allocation Theorem

• Previous page
• Next page

• Previous page
• Next page

# OVERVIEW OF THE THIRD MAIN CHAPTER #

In the first two chapters,  filter functions with real-valued frequency responses were mostly considered for reasons of presentation so that the associated time function is symmetric about zero-time. 

• However,  the impulse response of a realizable system must always be causal,  that is,  $h(t)$  must be identical to zero for  $t < 0$. 

• This strong asymmetry of the time function  $h(t)$  implies at the same time that the frequency response  $H(f)$  of a realizable system is always complex-valued with the exception of  $H(f) = K$  where there is a fixed relation between its real part and imaginary part.

• This third chapter provides a recapitulatory account of the description of causal realizable systems,  which differ also in the mathematical methods from those commonly used with non-causal systems.

In detail,  the following is dealt with:

1. The  »Hilbert transform«,  which states how real and imaginary parts of  $H(f)$  are related,
2. the  »Laplace transform«,  which yields another spectral function  $H_{\rm L}(p)$  for acausal  $h(t)$,
3. the description of realizable systems by the  »pole-zero plot«,  as well as
4. the  »inverse Laplace transform«  using the  function theory  $($»residue theorem«$)$.

For this chapter,  we recommend two of our multimedia offerings:

• the  $($German language$)$  learning video  "Rechnen mit komplexen Zahlen"   ⇒   "Arithmetic operations involving complex numbers",

• the  $($German language$)$  interactive SWF applet  "Kausale Systeme - Laplacetransformation"   ⇒   "Causal systems – Laplace transform".

Prerequisites for the entire third main chapter

In the first two chapters,  mostly real  $\text{transfer functions}$   $H(f)$  were considered for which the associated impulse response  $h(t)$  is consequently always symmetric with respect to the reference time  $t = 0$.  Such transfer functions

• are suitable to explain basic relationships in a simple way,
• but unfortunately are not realizable for reasons of causality.

This becomes clear if the definition of the impulse response is considered:

$\text{Definition:}$  The  »impulse response«  $h(t)$  is equal to the output signal  $y(t)$  of the system if an infinitely short impulse with an infinitely large amplitude is applied to the input at time  $t = 0$ :   $x(t) = δ(t)$.  Such an impulse is called a  $\text{Dirac delta impulse}$.

It is obvious that no impulse response can be realized for which  $h(t < 0) ≠ 0$  holds.

$\text{Definition:}$  For a  »causal system«  the impulse response  $h(t)$  is identical to zero for all times  $t < 0$.

The only real transfer function that satisfies the causality condition  "the output signal cannot start before the input signal"  is:

$$H(f) = K \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h(t) = K \cdot \delta(t).$$

All other real-valued transfer functions  $H(f)$  describe non-causal systems and thus cannot be realized by an (electrical) circuit network.

$\text{In other words:}$   Except for the transfer function  $H(f) = K,$  any realistic transfer function is complex.

• If  $K=1$  holds additionally,  the transfer function is said to be ideal. 
• Then,  the output signal  $y(t)$  is identical to the input signal  $x(t)$  – even without attenuation or amplification.

Real and imaginary part of a causal transfer function

Any causal impulse response  $h(t)$  can be represented as the sum

• of an even  (German:  "gerade"   ⇒   "g")  part  $h_{\rm g}(t)$ 
• and an odd  (German:  "ungerade"   ⇒   "u")  part  $h_{\rm u}(t)$:

$$\begin{align*} h_{ {\rm g}}(t) & = {1}/{2}\cdot \big[ h(t) + h(-t) \big]\hspace{0.05cm},\\ h_{ {\rm u}}(t) & = {1}/{2}\cdot \big[ h(t) - h(-t) \big] = h_{ {\rm g}}(t) \cdot {\rm sign}(t)\hspace{0.05cm} .\end{align*}$$

Here, the so-called  $\text{sign function}$  is used:

$${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ +1 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} { t < 0,} \\ { t > 0.} \\ \end{array}$$

$\text{Example 1:}$  The graph shows this splitting for a causal exponentially decreasing impulse response of a low-pass filter of first-order corresponding to  "Exercise 1.3Z":

Splitting of the impulse response into an even part and an odd part

$$h(t) = \left\{ \begin{array}{c} 0 \\ 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \begin{array}{c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c} { t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$

It can be seen that:

• $h_{\rm g}(t) = h_{\rm u}(t) = h(t)/2$  holds for positive times,
• $h_{\rm g}(t)$  and  $h_{\rm u}(t)$  differ only by the sign for negative times,
• $h(t) = h_{\rm g}(t) + h_{\rm u}(t)$  holds for all times, also at time  $t = 0$  (marked by circles).

Let us now consider the same issue in the spectral domain.  According to the  $\text{Assignment Theorem}$  the following holds for the complex transfer function:  

$$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} ,$$

where the following assignment is valid:

$${\rm Re} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm g}}(t)\hspace{0.05cm},$$

$${\rm j} \cdot {\rm Im} \left\{ H(f) \right\} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm u}}(t)\hspace{0.05cm}.$$

First,  this relationship between the real part and the imaginary part of  $H(f)$  shall be worked out using another example.

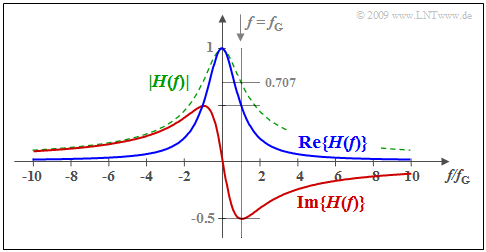
$\text{Example 2:}$  A low-pass filter of first-order is assumed and the following holds for its transfer function:

$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G} } = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$

Frequency response of a low-pass filter of first-order

Here,  $f_{\rm G}$  represents the  $\rm 3dB$  cut-off frequency at which  $\vert H(f)\vert^2$  has decreased to half of its maximum  $($at  $f = 0)$.  The corresponding impulse response  $h(t)$  has already been shown in  $\text{Example 1}$  for  $f_{\rm G} = 1/(2πT)$.

The graph shows the real part (blue) and the imaginary part (red) of  $H(f)$.  In addition, the magnitude is shown dashed in green.

Since the time functions  $h_{\rm g}(t)$  and  $h_{\rm u}(t)$  are related by the sign function, there also exists a fixed relationship

• between the real part   ⇒   ${\rm Re} \{H(f)\}$ 
• and the imaginary part   ⇒  ${\rm Im} \{H(f)\}$ 

of the transfer function  $\{H(f)\}$   ⇒   »Hilbert transform«.

This is described below.

Hilbert transform

Here,  two time functions  $u(t)$  and  $w(t) = \sign(t) · u(t)$  are considered in the most general sense.

• The associated spectral functions are denoted by  $U(f)$  and  ${\rm j} · W(f)$.
• That is:   In this section  ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {\rm j} \cdot W(f) }$  is valid and not the usual Fourier correspondence  ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, W(f)}.$

Using the correspondence   ${\rm sign}(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {1}/({{\rm j} \, \pi f })$   the following is obtained after writing the $\text{convolution integral}$ out in full with the integration variable  $ν$ :

$${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

However,  since at the same time   $u(t) = \sign(t) · w(t)$   also holds,  the following is valid in the same way:

$$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

These  "integral transformations"  are named after their discoverer  $\text{David Hilbert}$.

$\text{Definitions:}$  Both variants of the  »Hilbert transformation«  will be denoted by the following abbreviations in the further course:

$$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.8cm}{\rm or}\hspace{0.8cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$

• To calculate the spectrum marked by the arrowhead  –  here  $U(f)$   –  the equation with the positive sign is taken from the two otherwise identical upper equations:

$$U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

• The spectrum marked by the circle  –  here  $W(f)$   –  arises as a result from the equation with the negative sign:

$$ W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

Applying the Hilbert transformation twice yields the original function with a change of sign,  and applying it four times yields the original function including the correct sign:

$${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f),$$

$${\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$

$\text{Example 3:}$  In  [Mar94]  the following Hilbert correspondence can be found:

$$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$

• Here,  $x$  is representative of a suitably normalized time or frequency variable.
• For example,  if we use  $x = f/f_{\rm G}$  as a normalized frequency variable,  then we obtain the correspondence:

$$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

Based on the equation

$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$

the result found in  $\text{Example 2}$  is thus confirmed:

$${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

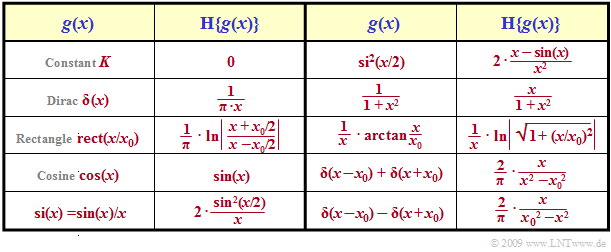
Some pairs of Hilbert correspondences

A very pragmatic way is followed to derive Hilbert correspondences, namely as follows:

• The  $\text{Laplace transform}$  $Y_{\rm L}(p)$  of function  $y(t)$ is computed as described in chapter  "Laplace Transform and p-Transfer Function".  This is already implicitly causal.

• $Y_{\rm L}(p)$  is converted into the associated Fourier spectrum  $Y(f)$  which is split it into real and imaginary parts.  To do this, the variable  $p$  is replaced by  ${\rm j \cdot 2}πf.$

Table with Hilbert correspondences

The real and imaginary parts – so  ${\rm Re} \{Y(f)\}$  and  ${\rm Im} \{Y(f)\}$ – are thus a pair of Hilbert transforms. Furthermore,

1.   the frequency variable  $f$  is substituted by  $x$,
2.   the real part  ${\rm Re} \{Y(f)\}$  by  $g(x)$,  and
3.   the imaginary part  ${\rm Im} \{Y(f)\}$  by  ${\cal H} \{g(x)\}$.

The new variable  $x$  can describe both a  (suitably)  normalized frequency or a  (suitably)  normalized time. Hence, the  $\text{Hilbert transformation}$  is applicable to various problems.

The table shows some of such Hilbert pairs. The signs have been omitted so that both directions are valid.

$\text{Example 4:}$  For example,  if  ${\cal H} \{g(x)\} = f(x)$  holds,  then from this it also follows that  ${\cal H} \{f(x)\} = \, –g(x)$.  In particular, it also holds:

$${\cal H}\left \{ \cos(x) \right\} = \sin(x)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\cal H}\left \{ \sin(x) \right\} = -\cos(x)\hspace{0.05cm}.$$

Attenuation and phase of minimum-phase systems

An important application of the Hilbert transformation is the relationship between attenuation and phase in the so-called  »minimum-phase systems«.  In anticipation of the following chapter  "Laplace Transform and p-Transfer Function",  it should be mentioned that these systems may have neither poles nor zeros in the right  $p$–half plane.

In general,  the following holds for the transfer function  $H(f)$  with the  $\text{complex transmission function}$  $g(f)$  and the attenuation function  $a(f)$  as well as the phase function  $b(f)$:

$$H(f) = {\rm e}^{-g(f)} = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} g(f) = a(f)+ {\rm j} \cdot b(f)\hspace{0.05cm}.$$

Now in the case of minimum-phase systems,  not only does the Hilbert transformation hold

• regarding imaginary and real part as it does for all realizable systems   ⇒   ${\rm Im} \left\{ H(f) \right \} \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, {\rm Re} \left\{ H(f) \right \}\hspace{0.01cm},$
• but additionally also the Hilbert correspondence between the phase and attenuation functions is valid   ⇒   $b(f) \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, a(f)\hspace{0.05cm}.$

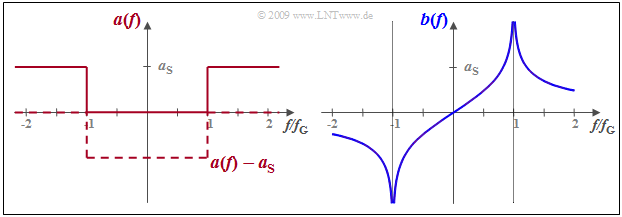
$\text{Example 5:}$   A low-pass filter has the frequency response  $H(f) = 1$   ⇒   $a(f) =0$  Np in the  "pass band"   ⇒    $\vert f \vert < f_{\rm G}$,  while for higher frequencies the attenuation function  $a(f)$  has the constant value  $a_{\rm S}$  (in Neper).

Attenuation and phase functions of an exemplary minimum-phase low-pass filter

• In this  "stop band"  ⇒    $\vert f \vert > f_{\rm G}$,   $H(f) = {\rm e}^{–a_{\rm S} }$  is very small but not zero.
• If the low-pass filter is to be causal and thus realizable, then the phase function  $b(f)$  must be equal to the Hilbert transform of the attenuation  $a(f)$ .
• Since the Hilbert transform of a constant is equal to zero, the function  $a(f) - a_{\rm S}$  can be assumed in the same way.
• This function shown dashed in the graph is  (negative)  rectangular between  $±f_{\rm G}$.  According to the  $\text{table}$  in the last section the following thus holds:

$$b(f) = {a_{\rm S} }/{\pi} \cdot {\rm ln}\hspace{0.1cm}\left\vert \frac{f+f_{\rm G} }{f-f_{\rm G} }\right \vert \hspace{0.05cm}.$$

In contrast, any other phase response would result in a non-causal impulse response.

Exercises for the chapter

Exercise 3.1: Causality Considerations

Exercise 3.1Z: Hilbert Transform