Laplace Transform and p-Transfer Function

Considered system model

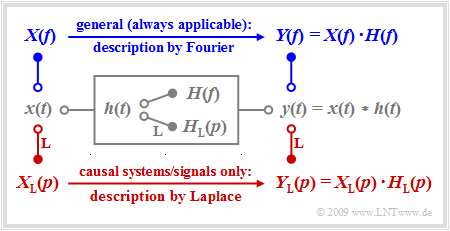
We consider a linear time-invariant system with the impulse response $h(t)$, whose input the signal $x(t)$ is applied to. The output signal $y(t)$ is then obtained as the convolution product $x(t) ∗ h(t)$.

General (also non-causal) and causal system model

For non-causal systems and signals, the $\text{first Fourier integral}$ must always be applied to describe the spectral behavior and the following is valid for the output spectrum:

$$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$

The Fourier integral also continues to be valid for causal systems and signals, i.e. under the assumption

$$x(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$

In this case, however, there are significant advantages in applying the Laplace transformation while taking into account certain restrictions:

The systems treated in this way are always realizable by a circuit. The developer is not tempted to offer unrealistic solutions.
The Laplace transform $X_{\rm L}(p)$ is always a real function of the spectral variable $p$. The fact that this variable is derived from the multiplication of the physical angular frequency $ω = 2πf$ by the imaginary unit $\rm j$ according to $p = {\rm j} · 2πf$ does not matter for the user.
The implicit condition $x(t) = 0$ for $t < 0$ specifically allows for simpler analysis of transient
behavior after switching-on processes than with the Fourier integral.

Definition of the Laplace transformation

Starting from the $\text{first Fourier integral}$

$$X(f) = \int_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t,$$

the Laplace transformation is obtained directly by using the formal substitution $p = {\rm j} · 2πf$ for a causal time function $x(t) = 0 \ \ \ \text{for} \ \ \ t < 0.$

$\text{Definition:}$ The »Laplace transform« of a causal time function $x(t)$ is:

$$X_{\rm L}(p) = \int_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t} }\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm briefly}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}.$$

The relationship between the Laplace transform $X_{\rm L}(p)$ and the physical spectrum $X(f)$ is often given as follows:

$$X(f) = X_{\rm L}(p) \Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}={\rm \hspace{0.05cm} j\hspace{0.05cm}2\pi \it f}}}.$$

However, if the signal $x(t)$ has periodic components and thus the spectral function $X(f)$ contains Dirac delta functions, then this equation is not applicable.
In this case, $p = α + {\rm j} · 2πf$ must be applied and then the limit $α → 0$ must be formed.

$\text{Example 1:}$ We assume the unilaterally and exponentially decreasing time function corresponding to the $\text{sketch}$ in $\text{Example 1}$ of the chapter "Conclusions from the Allocation Theorem":

$$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$

Thus, the Laplace transform is:

$$X_{\rm L}(p) = \int_{0}^{\infty} {\rm e}^{-t/T} \cdot {\rm e}^{-pt} \hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.08cm}\cdot \hspace{0.08cm}t}}\hspace{0.15cm}\Bigg \vert_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$

Considering $p = {\rm j} · 2πf$, the conventional spectral function with respect to $f$ is obtained:

$$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$

In contrast, if we consider the frequency response of a low-pass filter of first-order whose impulse response $h(t)$ differs from the above time function by the factor $1/T$, then the following holds for the Laplace transform and the Fourier transform, respectively:

$$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT} } = \frac {1}{1+{\rm j} \cdot f/f_{\rm G} } \hspace{0.05cm} .$$

In this equation, the 3dB cut-off frequency $($German: "Grenzfrequenz" ⇒ "G"$)$ $f_{\rm G} = 1/(2πT)$ is used instead of the parameter $T$.

Some important Laplace correspondences

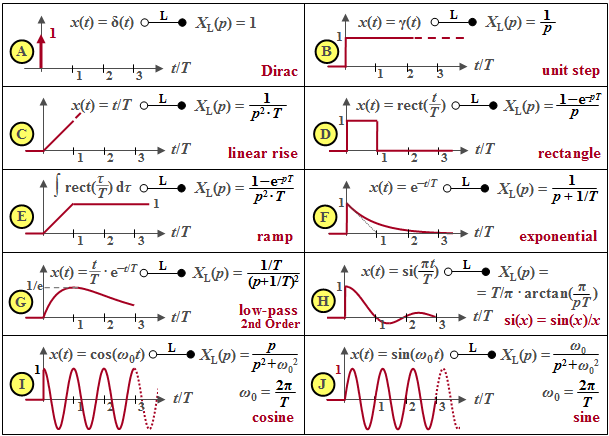
Some important Laplace correspondences are compiled subsequently. All time signals $x(t)$ considered here are assumed to be dimensionless. For this reason, $X_{\rm L}(p)$ then always has the unit "second" as an integral over time.

Table with some Laplace transforms

The Laplace transform of the $\text{Dirac delta function}$ $δ(t)$ is $X_{\rm L}(p) = 1$ $($diagram $\rm A)$. $X_{\rm L}(p) = 1/p$ is obtained for the unit step function $γ(t)$ $($diagram $\rm B)$ by applying the $\text{integration theorem}$. From this the Laplace transform of the linearly increasing function $x(t) = t/T$ for $t > 0$ is obtained by multiplication by $1/(pT)$ $($diagram $\rm C)$.

The $\text{rectangular function}$ can be generated from the subtraction of two step functions $γ(t)$ and $γ(t – T)$ separated by $T$ so that the Laplace transform $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ is obtained according to the $\text{shifting theorem}$ $($diagram $\rm D)$. By integration the ramp function or after multiplication by $1/(pT)$ its Laplace transform is obtained from it $($diagram $\rm E)$.

The exponential function $($diagram $\rm F)$ has already been considered in the "last section" . Considering the factor $1/T$, this is at the same time the impulse response of a low-pass filter of first-order. The $p$–spectral function of a low-pass filter of second-order with the time function $x(t) = t/T · {\rm e}^{–t/T}$ (diagram $\rm G$) is obtained by squaring.

In addition to the causal $\rm sinc$–function $($diagram $\rm H)$, the Laplace transforms of the causal cosine and sine functions $($diagrams $\rm I$ and $\rm J)$, which result in $p/(p^2 + ω_0^2)$ and $ω_0/(p^2 + ω_0^2)$ resp., are also given in the table. Here, $ω_0 = 2πf_0 = 2π/T$ denotes the so-called angular frequency.

Pole-zero representation of circuits

Any $\text{linear time-invariant system}$ $\rm (LTI)$ which can be realized by a circuit of discrete time-constant components such as

resistances $(R)$,
capacitances $(C)$,
inductances $(L)$ and
amplifier elements,

have a fractional-rational »$p$–transfer function«:

$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{...} + A_2 \cdot p^2 + A_1 \cdot p + A_0} {B_N \cdot p^N +\text{...} \ + B_2 \cdot p^2 + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$

All coefficients of the numerator ⇒ $A_Z, \text{...} \ , A_0$ and of the denominator ⇒ $B_N, \text{...} , B_0$ are real. Furthermore:

$Z$ denotes the degree of the numerator polynomial $Z(p)$,
$N$ denotes the degree of the denominator polynomial $N(p)$.

$\text{Equivalent pole-zero representation:}$ The following can be formulated for the $p$–transfer function, too:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i} } {\prod\limits_{i=1}^N p - p_{\rm x i} }= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \ \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

The $Z + N + 1$ parameters signify:

$K = A_Z/B_N$ is a constant factor. If $Z = N$ holds, then this is dimensionless.
The solutions of the equation $Z(p) = 0$ result in the $Z$ "zeros" $p_{\rm o1},\text{...} \ , p_{\rm oZ}$ of $H_{\rm L}(p)$.
The zeros of the denominator polynomial $N(p)$ yield the $N$ pole locations (or "poles" for short).

The transformation is unique. This can be seen from the fact that the $p$–transfer function is also determined only by $Z + N + 1$ free parameters according to the first equation since one of the coefficients $A_Z, \text{...} \ , A_0, B_N, \text{...} \ , B_0$ can be normalized to $1$ without changing the quotient.

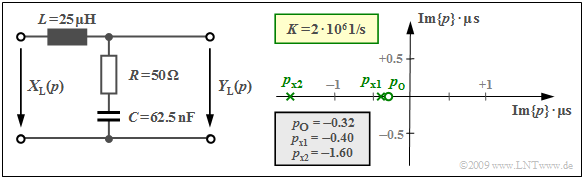
Considered two-port network and associated pole-zero diagram

$\text{Example 2:}$ We consider the drawn two-port network with an inductance $L$ $($complex resistance $pL)$ in the longitudinal branch as well as the series connection of an ohmic resistance $R$ and a capacitance $C$ with the complex resistance $1/(pC)$ in the transverse branch.

Thus, the $p$–transfer function is:

$$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {R + {1}/{(pC)} } {pL + R +{1}/{(pC)} }$$

$$\Rightarrow \hspace{0.3cm} H_{\rm L}(p)= \frac {1 + p \cdot{RC} } {1 + p \cdot{RC}+ p^2 \cdot{LC} } \hspace{0.05cm} .$$

If $p = {\rm j} · 2πf$ is set, then the Fourier transfer function (or the frequency response) is obtained. If the numerator and denominator in the above equation are divided by $LC$, then the following is obtained:

$$H_{\rm L}(p)= \frac {R} {L}\cdot \frac {p + {1}/{(RC)} } {p^2 + {R}/ {L}\cdot p + {1}/{(LC)} }= K \cdot \frac {p - p_{\rm o } } {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$

In the right-hand side of the equation, the transfer function $H_{\rm L}(p)$ is given in pole-zero notation. By comparison of coefficients the following values are obtained for $R = 50 \ \rm Ω$, $L = 25\ \rm µ H$ and $C = 62.5 \ \rm nF$ :

the constant $K = R/L = 2 · 10^6 \cdot 1/{\rm s}$,
the zero $p_{\rm o} = -1/(RC) = -0.32 · 10^6 \cdot 1/{\rm s},$
the two poles $p_{\rm x1}$ and $p_{\rm x2}$ as the solution of the equation

$$p^2 + \frac {R} {L}\cdot p + \frac{1}{LC} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -\frac {R} {2L}\pm \sqrt{\frac {R^2} {4L^2}- \frac{1}{LC} }$$

$$\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -10^6 \cdot {1}/{\rm s} \pm \sqrt{10^{12} \cdot {1} /{\rm s^2}-0.64 \cdot 10^{12} \cdot {1}/ {\rm s^2} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm x 1 }= -0.4 \cdot 10^6\cdot {1}/ {\rm s},\hspace{0.2cm}p_{\rm x 2 }= -1.6 \cdot 10^6\cdot {1}/ {\rm s} \hspace{0.05cm} .$$

In the above graph, the pole-zero diagram is given on the right-hand side.

The two axes denote the real and imaginary parts of the variable $p$, each normalized to the value $10^6 · \rm 1/s\; (= 1/µs)$.
The zero at $p_{\rm o} =\, –0.32$ can be seen as a circle and the poles at $p_{\rm x1} = \,–0.4$ and $p_{\rm x2} = \,–1.6$ as crosses.

Properties of poles and zeros

The transfer function $H_{\rm L}(p)$ of any realizable circuit is fully described by $Z$ "zeros" and $N$ "poles" together with a constant $K$ where the following restrictions apply:

$Z ≤ N$ always holds. The $p$–transfer function would also be "infinitely large" with $Z > N$ in the limiting case for $p → ∞$ (i.e. for very high frequencies).
The zeros $p_{\rm oi}$ and the poles $p_{ {\rm x}i}$ are generally complex, and have like $p$ the unit $\rm 1/s$. If $Z < N$ holds, then the constant $K$ has also a unit.
The poles and zeros can be real as shown in the last example. If they are complex, then two poles and two zeros always occur as complex conjugates, respectively, since $H_{\rm L}(p)$ always represents a real fractional-rational function.
All poles lie in the left half-plane or on the imaginary axis (limiting case). This property follows from the required and assumed causality together with the $\text{fundamental function theory}$, which will be stated in the next chapter.
Zeros can occur in both the left and right $p$–half-planes or also on the imaginary axis. An example of zeros in the right half-plane can be found in "Exercise 3.4Z", which deals with all-pass filters.
In so-called "minimum-phase systems", not only poles are forbidden in the right $p$–half-plane but also zeros. The real part of all singularities here is never positive.

These properties are now illustrated by three examples.

$\text{Example 3:}$ Starting from the $\text{two-port network}$ $(L$ in the longitudinal branch, $R$ and $C$ in the transverse branch$)$ the characteristic quantities of the transfer function can be given as follows:

$$K = 2A, \hspace{0.2cm}p_{\rm x 1,\hspace{0.05cm}2 }= -A \pm \sqrt{A^2-B^2}, \hspace{0.2cm}p_{\rm o }= - \frac{B^2}{2A} \hspace{0.05cm} \hspace{0.2cm} {\rm with } \hspace{0.2cm} A = \frac {R} {2L}, \hspace{0.2cm}B = \frac{1}{\sqrt{LC} } \hspace{0.05cm}.$$

The graph shows three different diagrams with different capacitance values $C$. $R = 50 \ \rm Ω$ and $L = 25 \ \rm µ H$ always hold. The axes are normalized to the variable $A = R/(2L) = 10^6 · \rm 1/s$ and the constant factor in each case is $K = 2A = 2 · 10^6 · \rm 1/s.$

Location of the zero and the poles for $Z = 1$ and $N = 2$

For $B < A$, »two real poles« and a zero to the right of $-A/2$ are obtained. The following arises as a result for $C = 62.5 \ \rm nF$ ⇒ $ {B}/ {A}= 0.8 $ (left diagram):

$$ p_{\rm x 1}/A = -0.4 , \hspace{0.2cm}p_{\rm x 2}/A= -1.6 , \hspace{0.2cm}p_{\rm o}/A= -0.32 \hspace{0.05cm} .$$

For $B > A$, »two conjugate-complex poles« and a zero to the left of $-A/2$ are obtained. For $C = 8 \ \rm nF$ ⇒ $ {B}/ {A}= \sqrt{5} $ (right diagram):

$$p_{\rm x 1,\hspace{0.05cm}2 }/A= -1\pm {\rm j}\cdot 2,\hspace{0.2cm}p_{\rm o}/A\approx -2.5 \hspace{0.05cm} .$$

The case $A = B$ leads to »a real double pole« and a zero at $– A/2$. For $C = 400 \ \rm nF$ ⇒ $ {B}/ {A}= 1 $ (middle diagram):

$$ p_{\rm x 1}/A= p_{\rm x 2}/A= -1, \hspace{0.2cm}p_{\rm o}/A= -0.5 \hspace{0.05cm} .$$

The impulse responses $h(t)$ are obtained according to the following chapter "Inverse Laplace Transform" as follows:

For the left constellation, $h(t)$ is $\text{aperiodically decaying}$.

For the right constellation, $h(t)$ is $\text{attenuated-oscillatory}$.

The middle constellation is called the "$\text{critically attenuated case}$".

Graphical determination of attenuation and phase

Output diagram for the computation
of attenuation and phase

The $p$–transfer function is given in pole-zero notation:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z (p - p_{\rm o i})} {\prod\limits_{i=1}^N (p - p_{\rm x i})}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{...} \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{...} \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

The conventional frequency response $H(f)$ is obtained by replacing the argument $p$ of $H_{\rm L}(p)$ by ${\rm j} \cdot 2πf$ :

$$H(f)= K \cdot \frac {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 2})\cdot \text{...} \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} \hspace{-0.03cm} Z})} {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 2})\cdot \text{...}\cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

We now consider a fixed frequency $f$ and describe the distances and angles of all "zeros" (circles) by vectors:

$$R_{ {\rm o} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} i}= |R_{{\rm o} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm o} i} }, \hspace{0.3cm}i= 1, \text{...}\ , Z \hspace{0.05cm} .$$

We proceed in the same way for the "poles" (crosses):

$$R_{ {\rm x} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} i}= |R_{ {\rm x} i}| \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm}\cdot\hspace{0.03cm}\phi_{ {\rm x} i} }, \hspace{0.3cm}i= 1, \text{...}\ , N \hspace{0.05cm} .$$

The graph shows the magnitudes and phase angles for a system

with $Z = 2$ zeros (circles) in the right half-plane
and $N = 2$ poles (crosses) in the left half-plane.

Moreover, the constant $K$ is also to be considered.

The following can be written for the frequency response with this vector representation:

$$H(f)= K \cdot \frac {|R_{ {\rm o} 1}| \cdot |R_{ {\rm o} 2}|\cdot ... \cdot |R_{ {\rm o} \hspace{-0.03cm} Z}|} {|R_{ {\rm x} 1}| \cdot |R_{ {\rm x} 2}|\cdot \text{...} \cdot |R_{ {\rm x} \hspace{-0.03cm} N}|} \cdot {\rm e^{\hspace{0.03cm}{\rm j} \hspace{0.05cm}\cdot [ \phi_{ {\rm o} 1}\hspace{0.1cm}+ \hspace{0.1cm}\phi_{ {\rm o} 2} \hspace{0.1cm}+ \hspace{0.1cm}\hspace{0.1cm}\text{...}. \hspace{0.1cm} + \hspace{0.1cm}\phi_{ {\rm o} \hspace{-0.03cm}{\it Z}}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 1}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 2} \hspace{0.1cm}- \hspace{0.1cm}... \hspace{0.1cm} - \hspace{0.1cm} \phi_{ {\rm x} \hspace{-0.03cm}{\it N} }]} } \hspace{0.05cm} .$$

If $H(f)$ is expressed by the attenuation function $a(f)$ and the phase function $b(f)$ according to the generally valid relation $H(f) = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$, then the following result is obtained by comparing with the above equation:

With a suitable normalization of all dimensional quantities the following holds for the attenuation function in Neper $(1 \ \rm Np$ corresponds to $8.686 \ \rm dB)$:

$$a(f) = -{\rm ln} \hspace{0.1cm} K + \sum \limits_{i=1}^N {\rm ln} \hspace{0.1cm} |R_{ {\rm x} i}|- \sum \limits_{i=1}^Z {\rm ln} \hspace{0.1cm} |R_{ {\rm o} i}| \hspace{0.05cm} .$$

The phase function in radian $\rm (rad)$ arises as a result according to the upper sketch and is

$$b(f) = \phi_K + \sum \limits_{i=1}^N \phi_{ {\rm x} i}- \sum \limits_{i=1}^Z \phi_{ {\rm o} i}\hspace{0.2cm}{\rm with} \hspace{0.2cm} \phi_K = \left\{ \begin{array}{c} 0 \\ \pi \end{array} \right. \begin{array}{c} {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c} { K > 0\hspace{0.05cm},} \\ { K <0\hspace{0.05cm}.} \end{array}$$

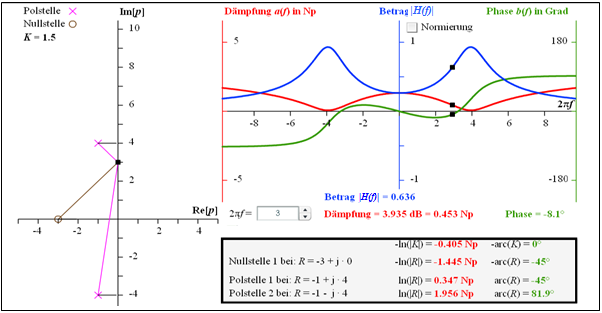
For the computation of the attenuation and phase functions (screen capture of the program "Causal Systems & Laplace Transformation" in an earlier German version)

$\text{Example 4:}$ The graphic illustrates the calculation

of the attenuation function $a(f)$ ⇒ red curve, and
of the phase function $b(f)$ ⇒ green curve

of a two-port network which is defined by the factor $K = 1.5$, one zero at $-3$ and two poles at $–1 \pm {\rm j} · 4$.

The given numerical values are valid for the frequency $2πf = 3$:

$$a \big [f = {3}/({2\pi}) \big ] = 0.453\,\,{\rm Np}= 3.953\,\,{\rm dB}$$

$$\Rightarrow \hspace{0.4cm}\big \vert H \big [f = {3}/({2\pi}) \big ]\big \vert = 0.636,$$

$$ b\big [f = {3}/({2\pi}) \big ] = -8.1^\circ \hspace{0.05cm} .$$

The derivation of these numerical values is illustrated in the framed block. For the magnitude frequency response $\vert H(f)\vert$ ⇒ blue curve, a band-pass-like curve shape is obtained with

$$\vert H(f = 0)\vert \approx 0.25\hspace{0.05cm},$$

$$\vert H(f = {4}/(2\pi)\vert \approx 0637\hspace{0.05cm},$$

$$\vert H(f \rightarrow \infty)\vert= 0 \hspace{0.05cm}.$$