xDSL as Transmission Technology

1 Possible bandwidth allocations for xDSL
2 ADSL bandwidth allocation in Germany
3 VDSL(2) bandwidth allocation
4 Overview of transmission methods
5 Basics of Quadrature Amplitude Modulation
6 Mögliche QAM-Signalraumkonstellationen
7 Carrierless Amplitude Phase Modulation (CAP)
8 Grundlagen von DMT – Discrete Multitone Transmission
9 DMT–Realisierung mit IDFT/DFT
10 Aufgaben zum Kapitel

Possible bandwidth allocations for xDSL

The xDSL specifications give operators a great deal of freedom with regard to allocation.

For the necessary directional separation of the xDSL signal transmission according to

downstream direction from the provider to the customer (downstream with the highest possible data rate),
upstream direction from the customer to the provider (upstream with mostly lower data rate)

two variants have been standardized for this purpose:

$\text{Definition:}$

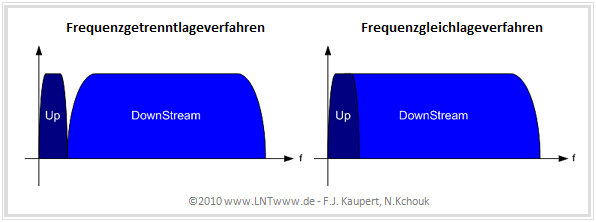
In the Frequenzgetrenntlageverfahren the data streams for the two directions are transmitted in two separate frequency bands with the advantage that a simple filter is sufficient to separate the transmission directions, which simplifies the technical implementation.
In the Frequenzgleichlageverfahren the spectra of upstream and downstream overlap in a certain part. The separation is done here with the help of an echo cancellation circuit. Advantages of the method are the lower bandwidth requirement at higher (and thus more attenuated) frequencies, as well as a longer range.

Frequenzgetrennt- und Frequenzgleichlageverfahren

The graphic compares these two options.

Basically, the specifications leave it up to the developers/operators to decide,

to operate xDSL alone on the subscriber line, or
to allow mixed operation of xDSL with the telephone services POTS (Plain Old Telephone Service) or ISDN (Integrated Services Digital Network) ,
and thus to exclude or also occupy the lower frequency range occupied by the two telephone services for xDSL.

ADSL bandwidth allocation in Germany

Because it is technically much easier to implement, the decision was made in favor of ADSL and ADSL2+ in Germany.

ADSL bandwidth allocation in Germany

of the Frequenzgetrenntlageverfahren,
the general reservation of the lower frequency range for ISDN.

The Frequenzgleichlageverfahren is still used in some cases, but rather rarely.

For the transmission methods

"QAM" (quadrature amplitude modulation) and
"CAP" (Carrierless Amplitude Phase Modulation)

the bandwidth available for DSL is not further decomposed.

In contrast, in the multicarrier method "DMT" (Discrete Multitone Transmission), the uplink channel and the downlink channel are divided into $N_{\rm Up}$ respectively. $N_{\rm Down}$ bins of 4.3125 kHz each.
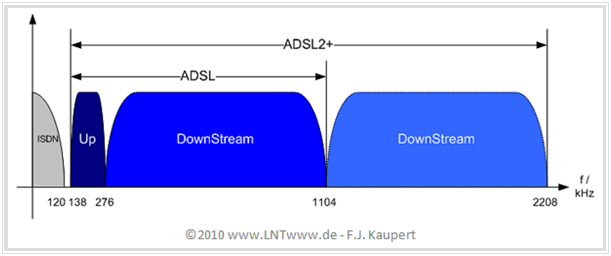
In addition to the above graph, it should be noted:

Phone services (POTS or ISDN) and xDSL are in different frequency bands, which minimizes mutual interference in the trunk cable. Thus, the stronger signal ISDN does not interfere with the parallel running xDSL and vice versa.
The lower frequency range up to $\text{120 kHz}$ has been reserved for ISDN (optionally POTS). This value results from the first zero of the "ISDN spectrum with 4B3T coding". Above $\text{120 kHz}$ the ISDN spectrum is completely suppressed.
To separate the telephone and xDSL signals, a "splitter" is used at both ends of the two-wire line, which includes one low-pass filter and one high-pass filter each and also takes into account the following frequency gap up to $\text{138 kHz}$ .
After this occupancy gap follows the ADSL upstream band from $\text{138 kHz}$ to $\text{276 kHz}$ . This bandwidth allows the transmission of $N_{\rm Up} = 32$ subcarriers at $\text{4.3125 kHz}$ each. This value is derived from the frame transmission rate.
The subsequent downstream range extends to $\text{1104 kHz}$ for ADSL, with which $N_{\rm Down} = 256$ subcarriers can be realized. The separation of up and down channel in xDSL is done by a bandpass filter in the modem.
However, the first $64$ subcarriers $($ this corresponds to $\text{276 kHz)}$ must not be occupied. With "Frequenzgleichlageverfahren" only $32$ subcarriers would have to be left out, taking into account that the separation of uplink and downlink requires a more complex implementation.
For ADSL2+, the system bandwidth is equal to $\text{2208 kHz}$ ⇒ $N_{\rm Down} = 512$ subcarriers. The number of bins to be spared remains unchanged compared to ADSL. Taking into account that two bins are occupied by control functions (e.g. for synchronization of transmitter and receiver), $190$ (ADSL) or $446$ (ADSL2+) downstream channels remain for users.
The ISDN reservation prescribed in Germany, however, has the consequence for xDSL that the low frequencies, which are by far the least attenuated in a copper line and would therefore actually be the most suitable, cannot be used.
Further, from the frequency arrangement, it can be seen that the downstream bins are more attenuated than the upstream bins (higher frequencies) and consequently have a smaller signal-to-noise ratio (SNR).
The decision "upstream below downstream" is related to the fact that the loss of downstream channels has only a comparatively small impact on the transmission rate. In the upstream, such a failure would be much more noticeable in percentage terms.

VDSL(2) bandwidth allocation

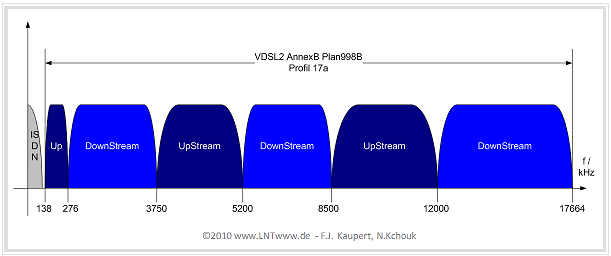
The ITU has defined several profiles for VDSL(2). At the time of writing this chapter (2010), the frequency band assignment specified in the graphic applies to the systems deployed in Germany in accordance with the ITU's VDSL(2) Plan 998b - Profile 17a (Annex B). The (slightly) lighter coloring at the higher frequencies is meant to indicate that these channels are more attenuated.

VDSL(2) bandwidth allocation in Germany

Without claiming to be exhaustive, this allocation plan can be characterized as follows:

To achieve higher bit rates, eight times as many bins are used here as in ADSL2+. Thus, the system bandwidth is $8 - \text{2208 MHz = 17664 MHz}$ , enabling transmission rates of up to $\text{100 Mbit/s}$ (depending on cable length and condition).
Also here, the frequency bands for the upstream subchannels are always arranged at the lower frequencies, since the greater cable attenuation (increasing with frequency) has a greater percentage influence on the total bit rate for upstream than for downstream.
In VDSL(2) systems, the so-called "Frequenzgetrenntlageverfahren" is always used. Overlapping of the upstream and downstream frequency bands is categorically excluded in the ITU specification for VDSL(2).
In the VDSL systems in Germany, the lower frequencies are again reserved for ISDN. This is followed by alternating ranges for upstream and downstream. From the specified range limits, one can recognize the upstream ranges, which are narrower than the downstream.
You can see an alternating arrangement of upstream and downstream areas. One reason for this is that with this wide spectrum it should be avoided that one direction (for example downstream) is assigned only strongly attenuated (i.e. high) frequencies.
The VDSL(2) specification provides for allocation plans up to system bandwidths of $\text{30 MHz}$ (according to profile 30a), which should enable transmission rates up to about $\text{ 200 Mbit/s}$ over short distances. For this purpose, the bandwidth of the individual subchannels is also doubled compared to ADSL to $\text{8.625 kHz}$ .
All occupancy plans are provided with different masks for the power density spectrum in order to limit the maximum transmit power and thus the interference to neighboring systems in the cable bundle (crosstalk).

Overview of transmission methods

At the beginning of the various standardization procedures for the individual xDSL variants, different transmission methods were defined as a basis:

"Pulse Code Modulation (PCM)" for ISDN as well as Trellis Coded-Pulse Amplitude Modulation for HDSL2 and SHDSL/SDSL,
"Quadrature Amplitude Modulation (QAM)" for QAM-ADSL and QAM-VDSL,
"Carrierless Amplitude Phase Modulation (CAP)" for CAP-HDSL and CAP-ADSL,
"Discrete Multitone Transmission (DMT)" for ADSL, ADSL2, ADSL 2+, VDSL and VDSL2.

With increasing market demand for higher transmission rates and the associated requirements, two main suitable processes crystallized, namely $\rm QAM/CAP$ and $\rm DMT$ .

Since the manufacturers were unable to agree on a common standard from 1997 to 2003, also for patent reasons (one even speaks of line code wars in this context), the two competing methods coexisted for a long time. At the so-called DSL Olympics in 2003, the decision was finally made in favor of DMT,

on the one hand because of the slightly better "performance" in general,
but in particular because of its higher robustness against narrowband interference.

Especially for the USA (many overhead telephone lines and related problems with coupled radio signals) the second argument played a major role.

The xDSL variants ADSL2(+) and VDSL(2), which are predominantly offered in Germany today (2010), are all based on the Discrete Multitone Transmission method, although the individual subcarriers may well be occupied by QAM signals.

First, however, the systems $\rm xDSL-QAM$ and $\rm xDSL-CAP$ will be considered very briefly.

Basics of Quadrature Amplitude Modulation

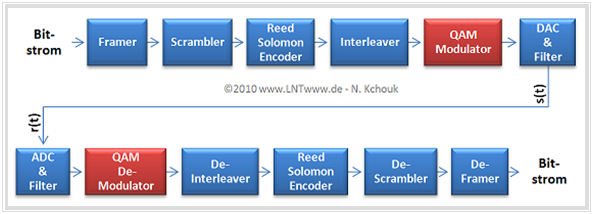
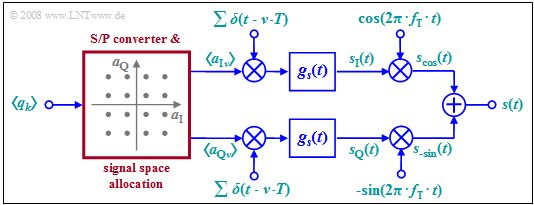
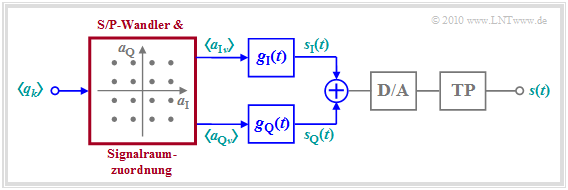
The diagram shows the reference model for ADSL-QAM, and here we will only deal with the red function blocks QAM modulator and QAM demodulator .

Reference model for ADSL QAM

The carrier frequency $f_{\rm T}$ is in each case within the specified uplink and downlink band of the respective xDSL variant. Like the signal space size (between four and 256 signal space points) and the symbol rate, it is determined by channel measurements during initialization of the transmission.

For ADSL QAM, the following symbol rates $($ in ${\rm kBaud} = 1000 \rm symbols/s)$ have been specified:

model of quadrature amplitude modulation

$20$ , $40$ , $84$ , $100$ , $120$ , $136$ upstream,
$40$ , $126$ , $160$ , $252$ , $336$ , $504$ , $806.4$ , $1008$ in the downstream.

The principle has already been described in detail in the chapter "Quadrature-Amplitude-Modation" of the book "Modulation Methods".

Here follows only a short summary on the basis of the lower diagram.

QAM ist ein Einträgermodulationsverfahren um die Trägerfrequenz $f_{\rm T}$ . Zunächst erfolgt eine blockweise Seriell–/Parallelwandlung des Bitstroms und die Signalraumzuordnung.
Aus jeweils $b$ Binärsymbolen werden zwei mehrstufige Amplitudenkoeffizienten $a_{{\rm I}n}$ und $a_{{\rm Q}n}$ abgeleitet (Inphase– und Quadraturkomponente), wobei beide Koeffizienten jeweils einen von $M = 2^{b/2}$ möglichen Amplitudenwerten annehmen können.
Das in der Grafik betrachtete Beispiel gilt für die $\text{16–QAM}$ mit $b = M = 4$ und dementsprechend $16$ Signalraumpunkten. Bei einer $\text{256–QAM}$ würde $b = 8$ und $M = 16$ gelten $(2^b = M^2 = 256)$ .
Die Koeffizienten $a_{{\rm I}n}$ und $a_{{\rm Q}n}$ werden jeweils einem Diracpuls als Gewichte eingeprägt. Zur Impulsformung verwendet man (wegen der geringen Bandbreite) meist ein Cosinus–Rolloff–Filter. Mit dem Sendegrundimpuls $g_s(t)$ gilt dann in den beiden Zweigen des Blockschaltbilds:

$s_{\rm I}(t) = \sum_{n = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it n} \cdot g_s (t - n \cdot T)\hspace{0.05cm},\hspace{0.5cm} s_{\rm Q}(t) = \sum_{n = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it n} \cdot g_s (t - n \cdot T)\hspace{0.05cm}.$

Anzumerken ist ferner, dass wegen der redundanzfreien Umsetzung auf einen höherstufigen Code die Symboldauer $T$ dieser Signale um den Faktor $b$ größer ist als die Bitdauer $T_{\rm B}$ der binären Eingangsfolge. Im gezeichneten Beispiel (16–QAM) gilt $T = 4 · T_{\rm B}$ .
Das QAM–Sendesignal $s(t)$ ist dann die Summe der beiden mit Cosinus bzw. Minus–Sinus multiplizierten Teilsignale (möglicherweise folgt noch eine Bandbegrenzung, um Interferenzen zu benachbarten Bändern zu verhindern, wie in der unteren Grafik angedeutet):

$s(t) = s_{\rm I}(t) \cdot \cos (2 \pi f_{\rm T}\,t) - s_{\rm Q}(t) \cdot \sin (2 \pi f_{\rm T}\,t) \hspace{0.05cm}.$

Die beiden Zweige $(\rm I$ und $\rm Q)$ können wegen der Orthogonalität von Cosinus– und (Minus–) Sinus als zwei völlig getrennte $M$ –stufige ASK–Systeme aufgefasst werden, die sich gegenseitig nicht stören, solange alle Komponenten optimal ausgelegt sind.
Das bedeutet gleichzeitig: Die Quadratur–Amplitudenmodulation ermöglicht gegenüber einer Binary Phase Shift Keying (BPSK: Modulation nur mit Cosinus oder Sinus) eine Verdoppelung der Datenrate bei gleichbleibender Qualität.

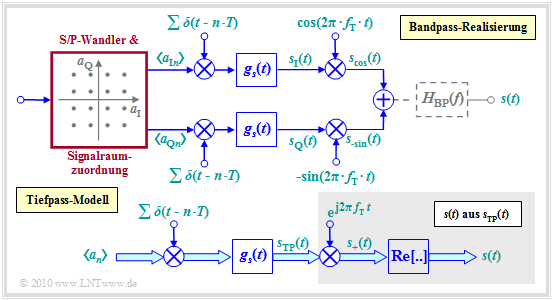
Quadratur–Amplitudenmodulation als Bandpass– und Tiefpassmodell

Die letzte Grafik zeigt

oben das Bandpass–Modell,
unten das äquivalente Tiefpass–Modell.

In diesem kombiniert man Inphase– und Quadraturkoeffizient zum komplexen Amplitudenkoeffizienten

$a_n = a_{\text{I}n} + {\rm j} · a_{\text{Q}n}$

und ersetzt zusätzlich das C–Signal $s(t)$ durch das äquivalente Tiefpass–Signal

$s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} · s_{\rm Q}(t).$

Die Darstellung des QAM–Senders und des QAM–Empfängers ist Inhalt der Flash–Animation Prinzip der Quadratur–Amplitudenmodulation.

$\text{Fazit:}$

Mit steigendem Bitanzahl $b$ und damit größerer Anzahl definierter Symbole $(M^2)$ nimmt die Bandbreiteneffizienz zu, aber es steigt auch der Aufwand für die Signalverarbeitung.
Außerdem ist zu berücksichtigen, dass eine dichte QAM–Belegung nur bei ausreichend gutem Kanal angemessen ist.

Mögliche QAM-Signalraumkonstellationen

Wir betrachten noch an drei Beispielen mögliche Anordnungen der Signalraumpunkte bei der Quadratur–Amplitudenmodulation.

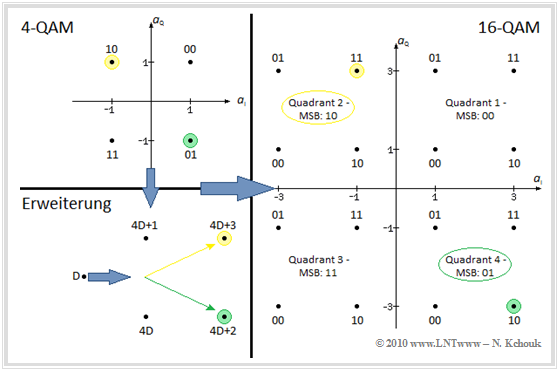
$\text{Beispiel 1:}$ Ein wichtiger QAM–Parameter ist die Bitanzahl $b$ , die zum Amplitudenkoeffizientenpaar $(a_{\rm I}, a_{\rm Q})$ verarbeitet werden. Hierbei ist $b$ stets geradzahlig.

Signalraumkonstellationen

$\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ und

$\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$

Ist $b = 2$ , so kann sowohl $a_{\rm I}$ als auch $a_{\rm Q}$ nur die Werte $±1$ annehmen und es ergibt sich die $\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ entsprechend der linken Konstellation.

Entsprechend einer ITU–Empfehlung gilt dabei die Zuordnung:

$q_1 = 0, \ q_0 = 0 \, \Leftrightarrow \,a_{\rm I} = +1, \ a_{\rm Q} = +1,$

$q_1 = 0, \ q_0 = 1 \, \Leftrightarrow \, a_{\rm I} = +1, \ a_{\rm Q} = -1,$

$q_1 = 1, \ q_0 = 0 \, \Leftrightarrow \,a_{\rm I} = -1, \ a_{\rm Q} = +1,$

$q_1 = 1, \ q_0 = 1 \, \Leftrightarrow \, a_{\rm I} = -1, \ a_{\rm Q} = -1.$

Der gelb markierte Punkt 10 $(a_{\rm I} = -1, \ a_{\rm Q} = 1)$ steht also für $q_1 = 1$ und $q_0 = 0$ .

Mit $b = 4$ ⇒ $M = 2^{b/2} = 4$ kommt man zur $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$ gemäß dem rechten Diagramm mit den möglichen Amplitudenkoeffizienten

$a_{\rm I} ∈ \{±3, ±1\}, \ \ a_{\rm Q} ∈ \{±3, ±1\}.$

Die Zuordnung lässt sich mit Hilfe des links unten angegebenen Hilfsgrafen ermitteln, wie die folgenden Zahlenbeispiele verdeutlichen.

$\rm (A)$ $q_3 = 1, \ q_2 = 0, \ q_1 = 1,\ q_0 = 1$ (gelbe Markierung):

Die beiden höchstwertigen Bit (Most Significant Bit, MSB) 10 bestimmen entsprechend dem $\rm 4-QAM$ –Diagramm den Quadranten, in dem das Symbol liegt.
Die beiden niederwertigen Bit (11) legen zusammen mit dem Hilfsgrafen den Punkt innerhalb des Quadranten fest. Das Ergebnis ist $a_{\rm I} = -1$ , $a_{\rm Q} = +3$ .

$\rm (B)$ $q_3 = 0, \ q_2 = 1, \ q_1 = 1,\ q_0 = 0$ (grüne Markierung):

Die beiden höchstwertigen Bit (Most Significant Bit, MSB) 01 verweisen hier auf den vierten Quadranten.
Die beiden niederwertigen Bit (10) verweisen auf den grünen Punkt im vierten Quadranten: $a_{\rm I} = -3, \ a_{\rm Q} = -3$ .

$\text{Beispiel 2:}$

Signalraumkonstellationen

$\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ und

$\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$

Eine weitere Möglichkeit zur Beschriftung der Punkte bietet der Dezimalwert $D$ .

Der gelb markierte Punkt im $\rm 4\hspace{0.05cm}–\hspace{-0.02cm}QAM$ –Diagramm ist binär mit 10 bezeichnet ⇒ dezimal $D = 2$ . Dieser Punkt markiert gleichzeitig den Quadranten der $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$ .
Die weitere Unterteilung ergibt sich aus der linken unteren Grafik. Dort steht beim gelben Punkt $4D + 3$ ⇒ 11 (dezimal). Deshalb steht der rechte obere Punkt (gelb markiert) im linken oberen Quadranten für dezimal $11$ ⇒ binär 1011.

Für den grünen Punkt ergibt sich mit $D = 1$ der Dezimalwert $4D + 2 ⇒ 6$ , was der binären Darstellung 0110 entspricht.

Nach diesem Schema lassen sich auch die Signalraumkonstellationen für $\rm 64\hspace{0.05cm}–\hspace{-0.02cm}QAM$ ⇒ $(b = 6, \ M = 8)$ und $\rm 256-QAM$ ⇒ $(b = 8, \ M = 16)$ entwickeln, worauf in der Aufgabe 2.3 im Detail eingegangen wird.

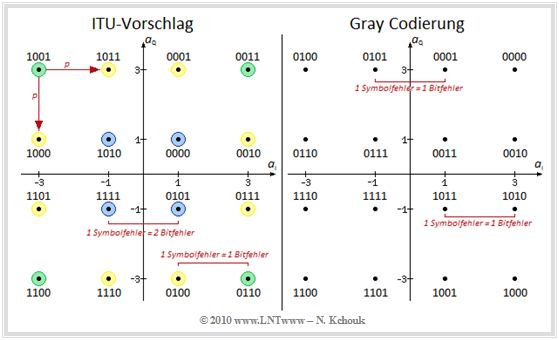
Zur Fehlerwahrscheinlichkeit bei

$\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$

$\text{Beispiel 3:}$ Wir betrachten noch für die beschriebene $\rm 16\hspace{0.05cm}–\hspace{-0.02cm}QAM$ (linke Grafik, hier als ITU-Vorschlag bezeichnet) die sich ergebende Fehlerwahrscheinlichkeit bei AWGN–Rauschen:

Es kann davon ausgegangen werden, dass ein Fehler zu einem horizontal oder vertikal benachbarten Symbol führt, wie für den linken oberen (grünen) Punkt angedeutet.
Die Fehlerwahrscheinlichkeit $p$ hängt von der Euklidischen Distanz der beiden Punkte und der AWGN–Rauschleistungsdichte $N_0$ ab.
Eine Verfälschung zum weiter entfernten blauen Punkt anstatt zu einem der beiden benachbarten gelben Punkte ist bei Gaußschem Rauschen eher unwahrscheinlich.

Alle Eckpunkte (grün hinterlegt) können nur in zwei Richtungen verfälscht werden. Dagegen haben die inneren QAM–Punkte (blau hinterlegt) vier direkte Nachbarn und die restlichen Symbole (gelb hinterlegt) drei. Für die (mittlere) Symbolfehlerwahrscheinlichkeit gilt dann:

$p_{\rm S} = {1}/{16} \cdot (4 \cdot 2 p + 8 \cdot 3 p + 4 \cdot 4 p) = 3p.$

Zur Berechnung der Bitfehlerwahrscheinlichkeit $p_{\rm B}$ muss nun berücksichtigt werden, dass bei der linken Konstellation ein Symbolfehler

nur zu einem Bitfehler (Beispiel: 0100 ⇒ 0110, innerhalb eines Quadranten) oder
zu zwei Bitfehlern (Beispiel: 1111 ⇒ 0101, zwischen benachbarten Quadranten)

führt. Die Berechnung von $p_{\rm B}$ ist hier mit einem gewissen Aufwand verbunden.

Dagegen unterscheidet sich bei einer Gray–Codierung (rechtes Diagramm) jedes Symbol von seinen Nachbarn um genau ein Bit, und jeder Symbolfehler hat somit genau nur einen Bitfehler zur Folge. Da jedes einzelne Symbol vier Bit beinhaltet, gilt in diesem Fall für die (mittlere) Bitfehlerwahrscheinlichkeit:

$p_{\rm B} = p_{\rm S}/4 = 3/4 \cdot p.$

Carrierless Amplitude Phase Modulation (CAP)

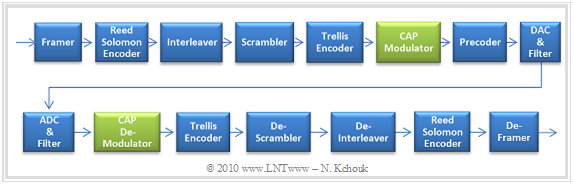
Carrierless Amplitude Phase Modulation (CAP) ist eine bandbreiteneffiziente Variante der QAM, die sich mit digitalen Signalprozessoren sehr einfach realisieren lässt. Der Unterschied zur QAM liegt einzig darin, dass auf eine Modulation mit einem Trägersignal verzichtet werden kann.

Modell der Carrierless Amplitude Phase Modulation

Anstelle der Multiplikation mit Cosinus und Minus–Sinus wird hier eine digitale Filterung vorgenommen. $g_{\rm I}(t)$ und $g_{\rm Q}(t)$ sind die um $π/2$ phasenverschobenen Impulsantworten zweier transversaler Bandpassfilter mit gleicher Amplitudencharakteristik.
Beide sind zueinander orthogonal, das heißt, dass das Integral des Produkts $g_{\rm I}(t) · g_{\rm Q}(t)$ über eine Symboldauer den Wert Null ergibt.
Die so erzeugten Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ werden zusammengeführt, durch einen D/A–Wandler in ein zeitkontinuierliches Signal gewandelt und die bei der D/A–Wandlung erzeugten unerwünschten hochfrequenten Anteile vor dem Aussenden durch ein Tiefpassfilter (TP) eliminiert.
Beim Empfänger wird das Signal $r(t)$ zunächst mittels A/D–Wandler in ein zeitdiskretes Signal gewandelt und anschließend werden über zwei Finite–Impulse–Response–Filter (FIR–Filter) und nachgelagerte Entscheider die Inphase– und Quadratur–Symbole $a_{\rm I}$ und $a_{\rm Q}$ extrahiert.

Referenzmodell für CAP–ADSL

CAP war der de–facto–Standard bei den anfänglichen ADSL–Spezifikationen bis 1996.

Die Frequenzen bis $\text{4 kHz}$ wurden für POTS reserviert.
Der Aufwärtskanal belegte den Frequenzbereich von $\text{15 - 160 kHz}$ ,
und der Abwärtskanal die Frequenzen von $\text{240 kHz}$ bis $\text{1.5 MHz}$ .
Die Grafik zeigt das Referenzmodell.

Ein Problem bei CAP ist, dass ein „schlechter Kanal” dramatische Folgen auf die Übertragungsqualität hat. Deshalb findet man heute (2010) CAP–ADSL nur noch bei einigen wenigen HDSL–Varianten.

Grundlagen von DMT – Discrete Multitone Transmission

Discrete Multitone Transmission (DMT) bezeichnet ein Mehrträgermodulationsverfahren, das nahezu identisch mit Orthogonal Frequency Division Multiplexing (OFDM) ist. Bei leitungsgebundener Übertragung spricht man meist von „DMT”, bei drahtloser Übertragung von „OFDM”.

In beiden Fällen unterteilt man die gesamte Bandbreite in viele schmalbandige äquidistante Subkanäle. Die jeweiligen Subträgersignale $s_k(t)$ werden individuell mit komplexen Datensymbolen $D_k$ beaufschlagt und die Summe der modulierten Subträgersignale wird als Sendesignal $s(t)$ übertragen.

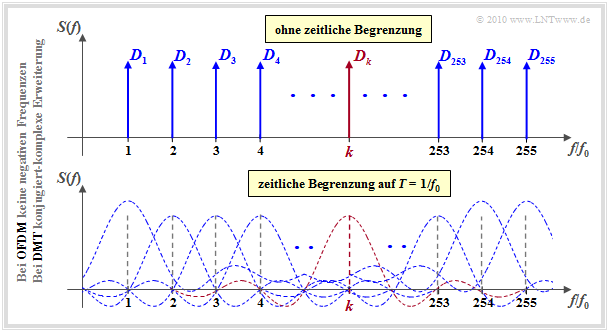
Die Grafik verdeutlicht das Prinzip von OFDM und DMT im Frequenzbereich, wobei teilweise die für ADSL/DMT spezifizierten Werte verwendet sind:

Spektren bei OFDM und DMT

$255$ Subträger mit den Trägerfrequenzen $k · f_0$ $(k = 1$ , ... , $255)$ .
Grundfrequenz $f_0 = 4.3125 \ \rm kHz$ , da $4000$ Datenrahmen pro Sekunde übertragen werden.
Nach $68$ Datenrahmen wird jeweils ein Synchronisationsrahmen eingefügt.
Aufgrund des zyklischen Präfix (siehe Kapitel Einfügen von Guard–Intervall und zyklischem Präfix) muss die Symboldauer $T = 1/f_0$ noch um den Faktor $16/17$ verkürzt werden.

Ein wesentlicher Unterschied zwischen OFDM und DMT besteht darin, dass

bei OFDM das dargestellte Spektrum $S(f)$ in Wirklichkeit ein äquivalentes Tiefpass-Spektrum $S_{\rm TP}(f)$ beschreibt und noch die Verschiebung um eine Trägerfrequenz $f_{\rm T}$ zu berücksichtigen ist:

$S_{\rm TP}(f ) = \sum_{k = 1}^{255} D_k \cdot \delta (f - k \cdot f_0)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} S(f) = \frac{1}{2} \big [ S_{\rm TP}(f - f_{\rm T}) + S^*_{\rm TP}(-(f + f_{\rm T}))\big ] \hspace{0.05cm},$

bei DMT dagegen noch die Anteile bei negativen Frequenzen berücksichtigt werden müssen, die mit den konjugiert–komplexen Spektralkoeffizienten zu gewichten sind:

$S(f ) = \sum_{k = 1}^{255} \big [ D_k \cdot \delta (f - k \cdot f_0) + D^*_k \cdot \delta (f + k \cdot f_0) \big ] \hspace{0.05cm}.$

$\text{Bitte beachten Sie:}$

Nach diesen Gleichungen besteht das komplexe OFDM–Signal $s_{\rm OFDM}(t)$ aus $K = 255$ komplexen Exponentialschwingungen.
Das DMT–Signal $s_{\rm DMT}(t)$ setzt sich aus ebenso vielen Cosinusschwingungen mit Frequenzen $k · f_0$ zusammen (volle Belegung voausgesetzt).
Trotz komplexer Koeffizienten $D_k$ , die sich bei QAM–Belegung der Träger ergeben, ist das DMT–Signal wegen der konjugiert–komplexen Ergänzungen bei negativen Frequenzen stets reell.

Sowohl bei OFDM als auch bei der DMT ist allerdings das Sendesignal $s(t)$ zeitlich genau auf die Symboldauer $T = 1/f_0 ≈ 232 \ {\rm µs}$ begrenzt, was der Multiplikation mit einem Rechteck der Dauer $T$ bedeutet. Im Spektralbereich entspricht dies der Faltung mit einer Spaltfunktion $\text{si}(πfT)$ :

Aus jeder Diracfunktion bei $k · f_0$ wird somit bei Berücksichtigung der zeitlichen Begrenzung eine si–Funktion an gleicher Stelle, wie im unteren Diagramm dargestellt.
Benachbarte Subträgerspektren überlappen sich zwar auf der Frequenzachse, aber exakt bei $k · f_0$ sind wieder die Koeffizienten $D_k$ zu erkennen, da alle anderen Spektren hier Nullstellen aufweisen.
Für die untere Grafik ist ein symmetrisches Rechteck angenommen. Ein Rechteck zwischen $0$ und $T$ hätte noch einen Phasenterm zur Folge. Es würde sich aber bezüglich $|S(f)|$ nichts ändern.

$\text{Beispiel 4:}$ Geht man von den für den ADSL–Downstream günstigen Voraussetzungen aus, nämlich dass

pro Sekunde $4000$ Rahmen übertragen werden,
stets alle Subträger aktiv sind $(K = 255)$ ,
jeder Träger mit einer 1024–QAM $(b = 10$ , laut ITU $8 ≤ b ≤ 15 )$ belegt ist, und
ideale Bedingungen herrschen, so dass die in der Grafik erkennbare Orthogonalität erhalten bleibt,

so ergibt sich für die maximale Daten(bit)rate $R_{\rm B,\ max} = 4000 · K · b ≈ 10 \ \rm Mbit/s$ .

Spezifiziert ist der ADSL–Downstream allerdings nur mit $2 \ \rm Mbit/s$ wegen

der Aussparung der $64$ untersten Träger wegen ISDN und Upstream,
der QAM–Belegung der stark gedämpften Träger mit weniger als $10$ Bit, und
der Berücksichtigung des zyklischen Präfix sowie einige betriebsbedingte Gründe.

DMT–Realisierung mit IDFT/DFT

MT–Gesamtsystem

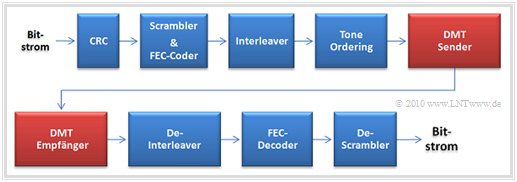
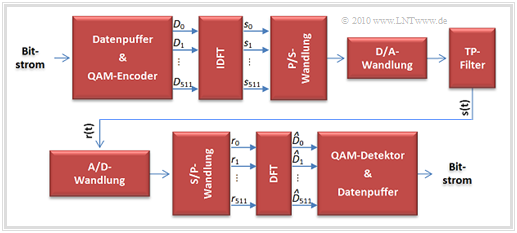
Die obere Grafik zeigt das DMT–Gesamtsystem, wobei wir uns zunächst auf die beiden roten Blöcke konzentrieren. Die blauen Blöcke werden im nächsten Kapitel behandelt.

DMT–Sender und –Empfänger

Vereinfacht lassen sich Sender und Empfänger wie in der linken Grafik darstellen:

Zur Durchführung der DMT–Modulation wird beim Sender ein Block an Eingangsbits in einem Datenpuffer angesammelt, der als ein Rahmen übertragen werden soll.
Der QAM–Coder liefert pro Rahmen die komplexwertigen Datensymbole $D_1$ , ... , $D_{255}$ , die mit $D_0 = D_{256} = 0$ sowie $D_k = D^\star_{512-k} \ (k = 257,$ ... , $511)$ zum Vektor $\mathbf{D}$ der Länge $512$ erweitert wird.
Als Konsequenz finiter Signale sind $D_{257}$ , ... , $D_{511}$ identisch mit $D_{–255}$ , ... , $D_{–1}$ .
Die Spektralabtastwerte $\mathbf{D}$ werden mittels der Inversen Diskreten Fouriertransformation (IDFT) in den Vektor $\mathbf{s}$ der Zeitsignalabtastwerte umgerechnet, ebenfalls mit Länge $512$ . Wegen der konjugiert–komplexen Belegung im Spektralbereich ist $\text{Im}[\mathbf{s}] = 0$ .

Nach Parallel/Seriell– und Digital/Analog–Wandlung und Tiefpassfilterung von $\text{Re}[\mathbf{s}]$ ergibt sich das physikalische und damit reelle sowie zeitkontinuierliche Sendesignal $s(t)$ . Für dieses gilt im Bereich $0 ≤ t ≤ T$ (Faktor $2$ , da jeweils zwei Koeffizienten zu Cosinus/Sinus beitragen):

$s(t) = \sum_{k = 1}^{255} \big [ 2 \cdot{\rm Re}\{D_k\} \cdot \cos(2\pi \cdot k f_0 \cdot t ) - 2 \cdot{\rm Im}\{D_k\} \cdot \sin(2\pi \cdot k f_0 \cdot t )\big ] \hspace{0.05cm}.$

Das Empfangssignal bei Übertragung über den AWGN–Kanal ist $r(t) = s(t) + n(t)$ . Nach A/D– und S/P–Wandlung kann $r(t)$ durch den (reellen) Vektor $\mathbf{r}$ ausgedrückt werden. Die Diskrete Fouriertransformation (DFT) liefert dann Schätzwerte für die gesendeten Spektralkoeffizienten.

Belegung des DMT–Frequenzbandes mit QAM-Koeffizienten

$\text{Beispiel 5:}$ Betrachten wir als Beispiel den ADSL/DMT–Downstream.

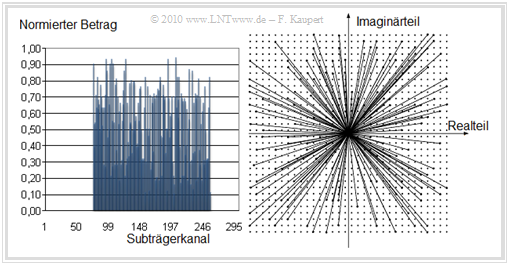
In der linken oberen Grafik erkennt man die Beträge $\vert D_k\vert$ der belegten Subkanäle $64$ , ... , $255$ . Die Träger $0$ , ... , $63$ für den reservierten Frequenzbereich von ISDN und Upstream sind auf Null gesetzt.
Rechts daneben sind die Spektralkoeffizienten $D_{64}$ , ... , $D_{255}$ in der komplexen Zahlenebene dargestellt, wobei der Signalraum sehr groß gewählt ist.

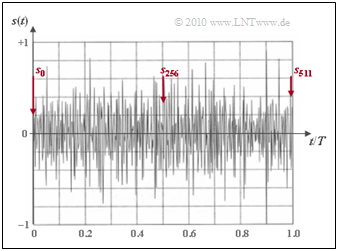
Sendesignal bei obiger DMT–Belegung

Die zweite (linke) Grafik zeigt das Sendesignal $s(t)$ für die Rahmendauer $T = {1}/{f_0} ≈ 232 \ \rm µs$ , das sich durch Tiefpass–Filterung der IDFT–Werte $s_0$ , ... , $s_{511}$ ergibt. Dieses Nutzsignal sieht nahezu aus wie Rauschen. Man erkennt:

Das Hauptproblem der DMT ist der ungünstige Crestfaktor ⇒ das Verhältnis von Maximalwert $s_{\rm max}$ und Effektivwert $s_{\rm eff}$ (Wurzel aus der mittleren Leistung).
Der im beispielhaften Signalverlauf erkennbare große Dynamikbereich stellt hohe Anforderungen an die Linearität der Verstärker.
Bei Begrenzung des Aussteuerbereichs werden die Spitzen von $s(t)$ abgeschnitten.
Dies wirkt wie eine Impulsstörung und eine zusätzliche Rauschbelastung für das System darstellt.

$\text{Zusammenfassend lässt sich sagen:}$

Discrete Multitone Transmission (DMT) ist im Prinzip die parallele Realisierung vieler schmalbandiger QAM–Modems mit unterschiedlichen Trägern und verhältnismäßig geringen Datenübertragungsraten. Die geringe Bandbreite pro Subträger ermöglicht eine lange Symboldauer, vermindert somit den Einfluss von Intersymbolinterferenzen und verringert den Entwicklungsaufwand für die Entzerrung.
Ein wesentlicher Grund für den Erfolg von DMT ist die technisch einfache Realisierung. IDFT und DFT werden mit digitalen Signalprozessoren in Echtzeit gebildet. Die Vektoren besitzen die Länge $512$ (Zweierpotenz). Deshalb kann der besonders schnelle FFT–Algorithmus (Fast Fourier Transformation) angewendet werden.