Difference between revisions of "Linear and Time Invariant Systems/Conclusions from the Allocation Theorem"
m (Text replacement - "Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation" to "Signal_Representation/Fourier_Transform_Laws") |
|||
| (95 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Description of Causal Realizable Systems |
| − | |Vorherige Seite= | + | |Vorherige Seite=Linear_Distortions |
| − | |Nächste Seite= | + | |Nächste Seite=Laplace_Transform_and_p-Transfer_Function |
}} | }} | ||
| − | == # | + | == # OVERVIEW OF THE THIRD MAIN CHAPTER # == |
<br> | <br> | ||
| − | In | + | In the first two chapters, filter functions with real-valued frequency responses were mostly considered for reasons of presentation so that the associated time function is symmetric about zero-time. |
| − | + | *However, the impulse response of a realizable system must always be causal, that is, $h(t)$ must be identical to zero for $t < 0$. | |
| + | |||
| + | *This strong asymmetry of the time function $h(t)$ implies at the same time that with exception of $H(f) = K$ the frequency response $H(f)$ of a realizable system is always complex-valued where there is a fixed relation between its real part and imaginary part. | ||
| + | |||
| + | *This third chapter provides a recapitulatory account of the description of causal realizable systems, which differ also in the mathematical methods from those commonly used with non-causal systems. | ||
| + | |||
| + | |||
| + | In detail, the following is dealt with: | ||
| − | + | #The »Hilbert transform«, which states how real and imaginary parts of $H(f)$ are related, | |
| + | #the »Laplace transform«, which yields another spectral function $H_{\rm L}(p)$ for acausal $h(t)$, | ||
| + | #the description of realizable systems by the »pole-zero plot«, as well as | ||
| + | #the »inverse Laplace transform« using the function theory $($»residue theorem«$)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | For this chapter, we recommend two of our multimedia offerings: | ||
| + | *the $($German language$)$ learning video [[Rechnen_mit_komplexen_Zahlen_(Lernvideo)|"Rechnen mit komplexen Zahlen"]] ⇒ "Arithmetic operations involving complex numbers", | ||
| − | + | *the $($German language$)$ interactive SWF applet [[Applets:Kausale_Systeme_-_Laplacetransformation|"Kausale Systeme - Laplacetransformation"]] ⇒ "Causal systems – Laplace transform". | |
| − | * | ||
| − | |||
| − | == | + | ==Prerequisites for the entire third main chapter== |
<br> | <br> | ||
| − | In | + | In the first two chapters, mostly real [[Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain#Frequency_response_–_Transfer_function|»transfer functions«]] $H(f)$ were considered for which the associated impulse response $h(t)$ is consequently always symmetric with respect to the reference time $t = 0$. Such transfer functions |
| − | * | + | *are suitable to explain basic relationships in a simple way, |
| − | * | + | |
| + | *but unfortunately are not realizable for reasons of causality. | ||
| − | + | This becomes clear if the definition of the impulse response is considered: | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The »'''impulse response'''« $h(t)$ is equal to the output signal $y(t)$ of the system if an infinitely short impulse with an infinitely large amplitude is applied to the input at time $t = 0$ : $x(t) = δ(t)$. Such an impulse is called a [[Signal_Representation/Special_Cases_of_Impulse_Signals#Dirac_delta_or_impulse|»Dirac delta impulse«]].}} | |
| − | + | It is obvious that no impulse response can be realized for which $h(t < 0) ≠ 0$ holds. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | For a »'''causal system'''« the impulse response $h(t)$ is identical to zero for all times $t < 0$.}} | |
| − | + | The only real transfer function that satisfies the causality condition »the output signal cannot start before the input signal« is: | |
:$$H(f) = K \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h(t) = K \cdot \delta(t).$$ | :$$H(f) = K \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h(t) = K \cdot \delta(t).$$ | ||
| − | + | All other real-valued transfer functions $H(f)$ describe non-causal systems and thus cannot be realized by an $($electrical$)$ circuit network. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{In | + | $\text{In other words:}$ Except for the transfer function $H(f) = K,$ '''any realistic transfer function is complex'''. |
| − | * | + | *If $K=1$ holds additionally, the transfer function is said to be »ideal«. |
| − | * | + | |
| + | *Then, the output signal $y(t)$ is identical to the input signal $x(t)$ – even without attenuation or amplification.}} | ||
| − | == | + | ==Real and imaginary part of a causal transfer function== |
<br> | <br> | ||
| − | + | Any causal impulse response $h(t)$ can be represented as the sum | |
| + | *of an even (German: "gerade" ⇒ "g") part $h_{\rm g}(t)$ | ||
| + | *and an odd (German: "ungerade" ⇒ "u") part $h_{\rm u}(t)$: | ||
:$$\begin{align*} h_{ {\rm g}}(t) & = {1}/{2}\cdot \big[ h(t) + h(-t) \big]\hspace{0.05cm},\\ h_{ {\rm u}}(t) & = {1}/{2}\cdot \big[ h(t) - h(-t) \big] = h_{ {\rm g}}(t) \cdot {\rm sign}(t)\hspace{0.05cm} .\end{align*}$$ | :$$\begin{align*} h_{ {\rm g}}(t) & = {1}/{2}\cdot \big[ h(t) + h(-t) \big]\hspace{0.05cm},\\ h_{ {\rm u}}(t) & = {1}/{2}\cdot \big[ h(t) - h(-t) \big] = h_{ {\rm g}}(t) \cdot {\rm sign}(t)\hspace{0.05cm} .\end{align*}$$ | ||
| − | + | Here, the so-called [https://en.wikipedia.org/wiki/Sign_function »sign function«] is used: | |
:$${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ | :$${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ | ||
+1 \\ \end{array} \right.\quad \quad | +1 \\ \end{array} \right.\quad \quad | ||
| − | \begin{array}{c} {\rm{ | + | \begin{array}{c} {\rm{for}} \\ {\rm{for}} |
\\ \end{array}\begin{array}{*{20}c} | \\ \end{array}\begin{array}{*{20}c} | ||
{ t < 0,} \\ | { t < 0,} \\ | ||
| Line 72: | Line 82: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | The graph shows this splitting for a causal exponentially decreasing impulse response of a low-pass filter of first-order corresponding to [[Aufgaben:Exercise_1.3Z:_Exponentially_Decreasing_Impulse_Response|$\text{Exercise 1.3Z}$]]: | |
| + | [[File: P_ID1750__LZI_T_3_1_S2a_neu.png |right|frame| Splitting of the impulse response into an even part and an odd part|class=fit]] | ||
:$$h(t) = \left\{ \begin{array}{c} 0 \\ | :$$h(t) = \left\{ \begin{array}{c} 0 \\ | ||
0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad | 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad | ||
| − | \begin{array}{c} {\rm{ | + | \begin{array}{c} {\rm{for} } \\ {\rm{for} } |
| − | \\ {\rm{ | + | \\ {\rm{for} } \end{array}\begin{array}{*{20}c} |
{ t < 0\hspace{0.05cm},} \\ | { t < 0\hspace{0.05cm},} \\ | ||
{ t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} | { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} | ||
| Line 83: | Line 94: | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | It can be seen that | |
| − | + | *$h_{\rm g}(t) = h_{\rm u}(t) = h(t)/2$ holds for positive times, | |
| − | + | ||
| − | * | + | *$h_{\rm g}(t)$ and $h_{\rm u}(t)$ differ only by the sign for negative times, |
| − | + | ||
| − | * | + | *$h(t) = h_{\rm g}(t) + h_{\rm u}(t)$ holds for all times, also at time $t = 0$ $($marked by circles$)$. }} |
| − | + | Let us now consider the same issue in the spectral domain. According to the [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|»'''Assignment Theorem'''«]] the following holds for the complex transfer function: | |
:$$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} | :$$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} | ||
,$$ | ,$$ | ||
| − | + | where the following assignment is valid: | |
:$${\rm Re} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm g}}(t)\hspace{0.05cm},$$ | :$${\rm Re} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm g}}(t)\hspace{0.05cm},$$ | ||
| Line 100: | Line 111: | ||
:$${\rm j} \cdot {\rm Im} \left\{ H(f) \right\} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm u}}(t)\hspace{0.05cm}.$$ | :$${\rm j} \cdot {\rm Im} \left\{ H(f) \right\} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm u}}(t)\hspace{0.05cm}.$$ | ||
| − | + | First, this relationship between real part and imaginary part of $H(f)$ shall be worked out using another example. | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | A low-pass filter of first-order is assumed and the following holds for its transfer function: | |
:$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G} } = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ | :$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G} } = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$ | ||
| − | + | [[File:P_ID1754__LZI_T_3_1_S2b_neu.png|right|frame|Frequency response of a first-order low-pass filter |class=fit]] | |
| + | Here, $f_{\rm G}$ represents the $\rm 3\hspace{0.05cm}dB$ cut-off frequency at which $\vert H(f)\vert^2$ has decreased to half of its maximum $($at $f = 0)$. The corresponding impulse response $h(t)$ has already been shown in $\text{Example 1}$ for $f_{\rm G} = 1/(2πT)$. | ||
| − | + | ⇒ The graph shows the real part $($blue$)$ and the imaginary part $($red$)$ of $H(f)$. In addition, the magnitude is shown dashed in green. | |
| − | + | Since the time functions $h_{\rm g}(t)$ and $h_{\rm u}(t)$ are related by the sign function, there also exists a fixed relationship | |
| − | + | * between the real part ⇒ ${\rm Re} \{H(f)\}$ | |
| − | + | ||
| − | + | * and the imaginary part ⇒ ${\rm Im} \{H(f)\}$ | |
| − | |||
| − | * | ||
| − | * | ||
| − | + | of the transfer function ${\cal H} \{H(f)\}$ ⇒ »'''Hilbert transform'''«. | |
| − | + | This is described below.}} | |
| − | == | + | ==Hilbert transform== |
<br> | <br> | ||
| − | + | Here, two time functions $u(t)$ and $w(t) = \sign(t) · u(t)$ are considered in the most general sense: | |
| − | * | + | *The associated spectral functions are denoted by $U(f)$ and ${\rm j} · W(f)$. |
| − | + | ||
| + | *That is: In this section ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {\rm j} \cdot W(f) }$ is valid and not the usual Fourier correspondence ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, W(f)}.$ | ||
| − | + | Using the correspondence ${\rm sign}(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {1}/({{\rm j} \, \pi f })$ the following is obtained after writing the [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_in_the_time domain|»convolution integral«]] out in full with the integration variable $ν$ : | |
:$${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | :$${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | ||
| − | + | However, since at the same time also holds $u(t) = \sign(t) · w(t)$, the following is valid in the same way: | |
:$$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | :$$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | ||
| − | + | These »integral transformations« are named after their discoverer [https://en.wikipedia.org/wiki/David_Hilbert $\text{David Hilbert}$]. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Definitions:}$ Both variants of the »'''Hilbert transformation'''« will be denoted by the following abbreviations in the further course: |
| − | :$$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.8cm}{\rm | + | :$$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.8cm}{\rm or}\hspace{0.8cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$ |
| − | * | + | *To calculate the spectrum marked by the arrowhead – here $U(f)$ – the equation with the positive sign is taken from the two otherwise identical upper equations: |
:$$U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | :$$U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$ | ||
| − | * | + | *The spectrum marked by the circle – here $W(f)$ – arises as a result from the equation with the negative sign: |
:$$ | :$$ | ||
W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$}} | W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$}} | ||
| − | + | Applying the Hilbert transformation twice yields the original function with a change of sign, and applying it four times yields the original function including the correct sign: | |
| − | :$${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f), | + | :$${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f),$$ |
| + | :$${\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ |
| − | In [Mar94]<ref name ='Mar94'>Marko, H.: | + | In [Mar94]<ref name ='Mar94'>Marko, H.: Methoden der Systemtheorie. 3. Auflage. Berlin – Heidelberg: Springer, 1994.</ref> the following Hilbert correspondence can be found: |
:$$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$ | :$$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$ | ||
| − | * | + | *Here, $x$ is representative of a suitably normalized time or frequency variable. |
| − | * | + | |
| + | *For example, if we use $x = f/f_{\rm G}$ as a normalized frequency variable, then we obtain the correspondence: | ||
:$$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$ | :$$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$ | ||
| − | + | Based on the equation | |
:$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$ | :$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$ | ||
| − | + | the result found in [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem#Real_and_imaginary_part_of_a_causal_transfer_function|$\text{Example 2}$]] is thus confirmed: | |
:$${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$}} | :$${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$}} | ||
| − | == | + | ==Some pairs of Hilbert correspondences== |
<br> | <br> | ||
| − | + | A very pragmatic way is followed to derive Hilbert correspondences, namely as follows: | |
| − | * | + | |
| − | + | *The [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function#Definition of the Laplace transformation|»Laplace transform«]] $Y_{\rm L}(p)$ of function $y(t)$ is computed as described in chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|»Laplace Transform and p-Transfer Function«]]. This is already implicitly causal. | |
| − | * | + | |
| − | + | *$Y_{\rm L}(p)$ is converted into the associated Fourier spectrum $Y(f)$ which is split into real and imaginary part. To do this, the variable $p$ is replaced by ${\rm j \cdot 2}πf.$ | |
| − | + | ||
| − | + | [[File:EN_LZI_T_3_1_S4.png|right|frame|Table with Hilbert correspondences|class=fit]] | |
| + | |||
| − | + | The real and imaginary parts – so ${\rm Re} \{Y(f)\}$ and ${\rm Im} \{Y(f)\}$ – are thus a pair of Hilbert transforms. Furthermore, | |
| + | # the frequency variable $f$ is substituted by $x$, | ||
| + | # the real part ${\rm Re} \{Y(f)\}$ by $g(x)$, and | ||
| + | # the imaginary part ${\rm Im} \{Y(f)\}$ by ${\cal H} \{g(x)\}$. | ||
| − | + | The new variable $x$ can describe both | |
| + | *a $($suitably$)$ normalized frequency | ||
| − | + | *or a $($suitably$)$ normalized time. | |
| + | |||
| + | Hence, the [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function#Representation with Hilbert transform|»Hilbert transformation«]] is applicable to various problems. The table shows some of such Hilbert pairs. The signs have been omitted so that both directions are valid. | ||
| + | <br clear=all> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ For example, if ${\cal H} \{g(x)\} = f(x)$ holds, then from this it also follows that |
| + | :$${\cal H} \{f(x)\} = \, –g(x).$$ | ||
| + | |||
| + | In particular, it also holds: | ||
:$${\cal H}\left \{ \cos(x) \right\} = \sin(x)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\cal H}\left \{ \sin(x) \right\} = -\cos(x)\hspace{0.05cm}.$$}} | :$${\cal H}\left \{ \cos(x) \right\} = \sin(x)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\cal H}\left \{ \sin(x) \right\} = -\cos(x)\hspace{0.05cm}.$$}} | ||
| − | == | + | ==Attenuation and phase of minimum-phase systems== |
<br> | <br> | ||
| − | + | An important application of the Hilbert transformation is the relationship between attenuation and phase in so-called »'''minimum-phase systems'''«. | |
| − | + | :In anticipation of the following chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|»Laplace Transform and p-Transfer Function«]], it should be mentioned that these systems may have neither poles nor zeros in the right $p$–half plane. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | In general, the following holds for the transfer function $H(f)$ with | ||
| + | # the [[Linear_and_Time_Invariant_Systems/Some_Results_from_Transmission_Line_Theory#Equivalent circuit diagram of a short transmission line section|»complex transmission function«]] $g(f)$ | ||
| + | #the attenuation function $a(f)$ and | ||
| + | # the phase function $b(f)$: | ||
| + | ::$$H(f) = {\rm e}^{-g(f)} = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} g(f) = a(f)+ {\rm j} \cdot b(f)\hspace{0.05cm}.$$ | ||
| + | Now in the case of minimum-phase systems, the Hilbert transformation does not only hold | ||
| + | *regarding imaginary and real part as it does for all realizable systems: | ||
| + | :$${\rm Im} \left\{ H(f) \right \} \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, {\rm Re} \left\{ H(f) \right \}\hspace{0.01cm},$$ | ||
| + | *but additionally also the Hilbert correspondence between the phase and attenuation functions is valid: | ||
| + | :$$b(f) \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, a(f)\hspace{0.05cm}.$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5:}$ |
| − | + | A low-pass filter has the frequency response $H(f) = 1$ ⇒ $a(f) =0$ Np in the »pass band« ⇒ $\vert f \vert < f_{\rm G}$, while for higher frequencies the attenuation function $a(f)$ has the constant value $a_{\rm S}$ $($in Neper$)$. | |
| − | + | [[File:P_ID1753__LZI_T_3_1_S5_neu.png|right|frame|Attenuation and phase functions of an exemplary minimum-phase low-pass filter|class=fit]] | |
| − | |||
| − | |||
| − | [[File:P_ID1753__LZI_T_3_1_S5_neu.png| | ||
| − | |||
| − | |||
| − | |||
| + | #In this »stop band« ⇒ $\vert f \vert > f_{\rm G}$, the frequency response $H(f) = {\rm e}^{–a_{\rm S} }$ is very small but not zero. | ||
| + | #If the low-pass filter is to be causal and thus realizable, then the phase function $b(f)$ must be equal to the Hilbert transform of the attenuation $a(f)$ . | ||
| + | #Since the Hilbert transform of a constant is zero, the function $a(f) - a_{\rm S}$ can be assumed in the same way. | ||
| + | #This function shown dashed in the graph is $($negative$)$ rectangular between $±f_{\rm G}$. According to the [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem#Some pairs of Hilbert correspondences|$\text{table}$]] in the last section the following thus holds: | ||
| + | ::$$b(f) = {a_{\rm S} }/{\pi} \cdot {\rm ln}\hspace{0.1cm}\left\vert \frac{f+f_{\rm G} }{f-f_{\rm G} }\right \vert \hspace{0.05cm}.$$ | ||
| − | + | $\text{Note:}$ | |
| − | + | In contrast, any other phase response would result in a non-causal impulse response.}} | |
| − | |||
| − | == | + | ==Exercises for the chapter== |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.1:_Causality_Considerations|Exercise 3.1: Causality Considerations]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.1Z:_Hilbert_Transform|Exercise 3.1Z: Hilbert Transform]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 19:21, 15 November 2023
Contents
# OVERVIEW OF THE THIRD MAIN CHAPTER #
In the first two chapters, filter functions with real-valued frequency responses were mostly considered for reasons of presentation so that the associated time function is symmetric about zero-time.
- However, the impulse response of a realizable system must always be causal, that is, $h(t)$ must be identical to zero for $t < 0$.
- This strong asymmetry of the time function $h(t)$ implies at the same time that with exception of $H(f) = K$ the frequency response $H(f)$ of a realizable system is always complex-valued where there is a fixed relation between its real part and imaginary part.
- This third chapter provides a recapitulatory account of the description of causal realizable systems, which differ also in the mathematical methods from those commonly used with non-causal systems.
In detail, the following is dealt with:
- The »Hilbert transform«, which states how real and imaginary parts of $H(f)$ are related,
- the »Laplace transform«, which yields another spectral function $H_{\rm L}(p)$ for acausal $h(t)$,
- the description of realizable systems by the »pole-zero plot«, as well as
- the »inverse Laplace transform« using the function theory $($»residue theorem«$)$.
For this chapter, we recommend two of our multimedia offerings:
- the $($German language$)$ learning video "Rechnen mit komplexen Zahlen" ⇒ "Arithmetic operations involving complex numbers",
- the $($German language$)$ interactive SWF applet "Kausale Systeme - Laplacetransformation" ⇒ "Causal systems – Laplace transform".
Prerequisites for the entire third main chapter
In the first two chapters, mostly real »transfer functions« $H(f)$ were considered for which the associated impulse response $h(t)$ is consequently always symmetric with respect to the reference time $t = 0$. Such transfer functions
- are suitable to explain basic relationships in a simple way,
- but unfortunately are not realizable for reasons of causality.
This becomes clear if the definition of the impulse response is considered:
$\text{Definition:}$ The »impulse response« $h(t)$ is equal to the output signal $y(t)$ of the system if an infinitely short impulse with an infinitely large amplitude is applied to the input at time $t = 0$ : $x(t) = δ(t)$. Such an impulse is called a »Dirac delta impulse«.
It is obvious that no impulse response can be realized for which $h(t < 0) ≠ 0$ holds.
$\text{Definition:}$ For a »causal system« the impulse response $h(t)$ is identical to zero for all times $t < 0$.
The only real transfer function that satisfies the causality condition »the output signal cannot start before the input signal« is:
- $$H(f) = K \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h(t) = K \cdot \delta(t).$$
All other real-valued transfer functions $H(f)$ describe non-causal systems and thus cannot be realized by an $($electrical$)$ circuit network.
$\text{In other words:}$ Except for the transfer function $H(f) = K,$ any realistic transfer function is complex.
- If $K=1$ holds additionally, the transfer function is said to be »ideal«.
- Then, the output signal $y(t)$ is identical to the input signal $x(t)$ – even without attenuation or amplification.
Real and imaginary part of a causal transfer function
Any causal impulse response $h(t)$ can be represented as the sum
- of an even (German: "gerade" ⇒ "g") part $h_{\rm g}(t)$
- and an odd (German: "ungerade" ⇒ "u") part $h_{\rm u}(t)$:
- $$\begin{align*} h_{ {\rm g}}(t) & = {1}/{2}\cdot \big[ h(t) + h(-t) \big]\hspace{0.05cm},\\ h_{ {\rm u}}(t) & = {1}/{2}\cdot \big[ h(t) - h(-t) \big] = h_{ {\rm g}}(t) \cdot {\rm sign}(t)\hspace{0.05cm} .\end{align*}$$
Here, the so-called »sign function« is used:
- $${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ +1 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} { t < 0,} \\ { t > 0.} \\ \end{array}$$
$\text{Example 1:}$ The graph shows this splitting for a causal exponentially decreasing impulse response of a low-pass filter of first-order corresponding to $\text{Exercise 1.3Z}$:
- $$h(t) = \left\{ \begin{array}{c} 0 \\ 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \begin{array}{c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c} { t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$
It can be seen that
- $h_{\rm g}(t) = h_{\rm u}(t) = h(t)/2$ holds for positive times,
- $h_{\rm g}(t)$ and $h_{\rm u}(t)$ differ only by the sign for negative times,
- $h(t) = h_{\rm g}(t) + h_{\rm u}(t)$ holds for all times, also at time $t = 0$ $($marked by circles$)$.
Let us now consider the same issue in the spectral domain. According to the »Assignment Theorem« the following holds for the complex transfer function:
- $$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} ,$$
where the following assignment is valid:
- $${\rm Re} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm g}}(t)\hspace{0.05cm},$$
- $${\rm j} \cdot {\rm Im} \left\{ H(f) \right\} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm u}}(t)\hspace{0.05cm}.$$
First, this relationship between real part and imaginary part of $H(f)$ shall be worked out using another example.
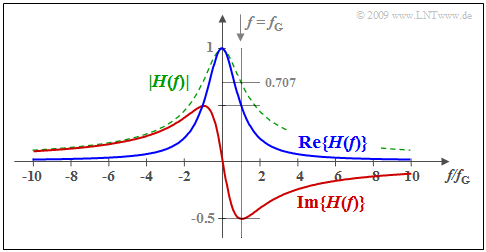
$\text{Example 2:}$ A low-pass filter of first-order is assumed and the following holds for its transfer function:
- $$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G} } = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$
Here, $f_{\rm G}$ represents the $\rm 3\hspace{0.05cm}dB$ cut-off frequency at which $\vert H(f)\vert^2$ has decreased to half of its maximum $($at $f = 0)$. The corresponding impulse response $h(t)$ has already been shown in $\text{Example 1}$ for $f_{\rm G} = 1/(2πT)$.
⇒ The graph shows the real part $($blue$)$ and the imaginary part $($red$)$ of $H(f)$. In addition, the magnitude is shown dashed in green.
Since the time functions $h_{\rm g}(t)$ and $h_{\rm u}(t)$ are related by the sign function, there also exists a fixed relationship
- between the real part ⇒ ${\rm Re} \{H(f)\}$
- and the imaginary part ⇒ ${\rm Im} \{H(f)\}$
of the transfer function ${\cal H} \{H(f)\}$ ⇒ »Hilbert transform«.
This is described below.
Hilbert transform
Here, two time functions $u(t)$ and $w(t) = \sign(t) · u(t)$ are considered in the most general sense:
- The associated spectral functions are denoted by $U(f)$ and ${\rm j} · W(f)$.
- That is: In this section ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {\rm j} \cdot W(f) }$ is valid and not the usual Fourier correspondence ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, W(f)}.$
Using the correspondence ${\rm sign}(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {1}/({{\rm j} \, \pi f })$ the following is obtained after writing the »convolution integral« out in full with the integration variable $ν$ :
- $${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
However, since at the same time also holds $u(t) = \sign(t) · w(t)$, the following is valid in the same way:
- $$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
These »integral transformations« are named after their discoverer $\text{David Hilbert}$.
$\text{Definitions:}$ Both variants of the »Hilbert transformation« will be denoted by the following abbreviations in the further course:
- $$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.8cm}{\rm or}\hspace{0.8cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$
- To calculate the spectrum marked by the arrowhead – here $U(f)$ – the equation with the positive sign is taken from the two otherwise identical upper equations:
- $$U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
- The spectrum marked by the circle – here $W(f)$ – arises as a result from the equation with the negative sign:
- $$ W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$
Applying the Hilbert transformation twice yields the original function with a change of sign, and applying it four times yields the original function including the correct sign:
- $${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f),$$
- $${\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$
$\text{Example 3:}$ In [Mar94][1] the following Hilbert correspondence can be found:
- $$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$
- Here, $x$ is representative of a suitably normalized time or frequency variable.
- For example, if we use $x = f/f_{\rm G}$ as a normalized frequency variable, then we obtain the correspondence:
- $$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$
Based on the equation
- $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$
the result found in $\text{Example 2}$ is thus confirmed:
- $${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$
Some pairs of Hilbert correspondences
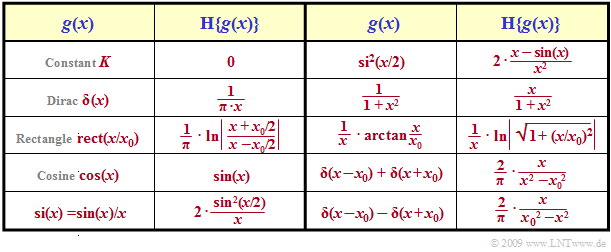
A very pragmatic way is followed to derive Hilbert correspondences, namely as follows:
- The »Laplace transform« $Y_{\rm L}(p)$ of function $y(t)$ is computed as described in chapter »Laplace Transform and p-Transfer Function«. This is already implicitly causal.
- $Y_{\rm L}(p)$ is converted into the associated Fourier spectrum $Y(f)$ which is split into real and imaginary part. To do this, the variable $p$ is replaced by ${\rm j \cdot 2}πf.$
The real and imaginary parts – so ${\rm Re} \{Y(f)\}$ and ${\rm Im} \{Y(f)\}$ – are thus a pair of Hilbert transforms. Furthermore,
- the frequency variable $f$ is substituted by $x$,
- the real part ${\rm Re} \{Y(f)\}$ by $g(x)$, and
- the imaginary part ${\rm Im} \{Y(f)\}$ by ${\cal H} \{g(x)\}$.
The new variable $x$ can describe both
- a $($suitably$)$ normalized frequency
- or a $($suitably$)$ normalized time.
Hence, the »Hilbert transformation« is applicable to various problems. The table shows some of such Hilbert pairs. The signs have been omitted so that both directions are valid.
$\text{Example 4:}$ For example, if ${\cal H} \{g(x)\} = f(x)$ holds, then from this it also follows that
- $${\cal H} \{f(x)\} = \, –g(x).$$
In particular, it also holds:
- $${\cal H}\left \{ \cos(x) \right\} = \sin(x)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\cal H}\left \{ \sin(x) \right\} = -\cos(x)\hspace{0.05cm}.$$
Attenuation and phase of minimum-phase systems
An important application of the Hilbert transformation is the relationship between attenuation and phase in so-called »minimum-phase systems«.
- In anticipation of the following chapter »Laplace Transform and p-Transfer Function«, it should be mentioned that these systems may have neither poles nor zeros in the right $p$–half plane.
In general, the following holds for the transfer function $H(f)$ with
- the »complex transmission function« $g(f)$
- the attenuation function $a(f)$ and
- the phase function $b(f)$:
- $$H(f) = {\rm e}^{-g(f)} = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} g(f) = a(f)+ {\rm j} \cdot b(f)\hspace{0.05cm}.$$
Now in the case of minimum-phase systems, the Hilbert transformation does not only hold
- regarding imaginary and real part as it does for all realizable systems:
- $${\rm Im} \left\{ H(f) \right \} \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, {\rm Re} \left\{ H(f) \right \}\hspace{0.01cm},$$
- but additionally also the Hilbert correspondence between the phase and attenuation functions is valid:
- $$b(f) \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, a(f)\hspace{0.05cm}.$$
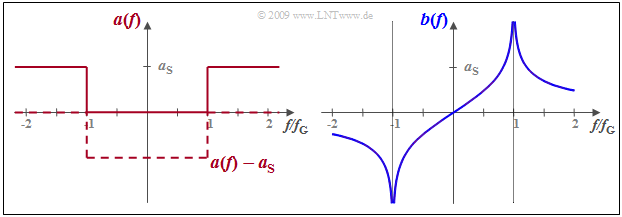
$\text{Example 5:}$ A low-pass filter has the frequency response $H(f) = 1$ ⇒ $a(f) =0$ Np in the »pass band« ⇒ $\vert f \vert < f_{\rm G}$, while for higher frequencies the attenuation function $a(f)$ has the constant value $a_{\rm S}$ $($in Neper$)$.
- In this »stop band« ⇒ $\vert f \vert > f_{\rm G}$, the frequency response $H(f) = {\rm e}^{–a_{\rm S} }$ is very small but not zero.
- If the low-pass filter is to be causal and thus realizable, then the phase function $b(f)$ must be equal to the Hilbert transform of the attenuation $a(f)$ .
- Since the Hilbert transform of a constant is zero, the function $a(f) - a_{\rm S}$ can be assumed in the same way.
- This function shown dashed in the graph is $($negative$)$ rectangular between $±f_{\rm G}$. According to the $\text{table}$ in the last section the following thus holds:
- $$b(f) = {a_{\rm S} }/{\pi} \cdot {\rm ln}\hspace{0.1cm}\left\vert \frac{f+f_{\rm G} }{f-f_{\rm G} }\right \vert \hspace{0.05cm}.$$
$\text{Note:}$ In contrast, any other phase response would result in a non-causal impulse response.
Exercises for the chapter
Exercise 3.1: Causality Considerations
Exercise 3.1Z: Hilbert Transform
References
- ↑ Marko, H.: Methoden der Systemtheorie. 3. Auflage. Berlin – Heidelberg: Springer, 1994.