Difference between revisions of "Linear and Time Invariant Systems/Linear Distortions"
| (59 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Signal Distortion and Equalization |
| − | |Vorherige Seite= | + | |Vorherige Seite=Nonlinear_Distortions |
| − | |Nächste Seite= | + | |Nächste Seite=Conclusions_from_the_Allocation_Theorem |
}} | }} | ||
| − | == | + | ==Compilation of important descriptive quantities== |
<br> | <br> | ||
| − | + | Now nonlinear distortions are excluded so that the system is fully described by the frequency response $H(f)$ . | |
| − | Now nonlinear distortions are excluded so that the system is fully described by the frequency response $H(f)$ . | ||
| − | The generally complex frequency response can also be formulated as follows: | + | {{BlaueBox|TEXT= |
| − | :$$H(f) = | + | [[File:P_ID899__LZI_T_2_3_S1_neu.png |frame|Linear system description|class=fit]] |
| − | \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} | + | $\text{System model:}$ |
| + | The »'''generally complex frequency response'''« can also be formulated as follows: | ||
| + | :$$H(f) = \vert H(f) \vert \cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \cdot | ||
| + | \hspace{0.05cm} b(f)} = {\rm e}^{- a(f)}\cdot {\rm e}^{- {\rm j} | ||
\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | ||
| − | |||
This yields the following descriptive quantities: | This yields the following descriptive quantities: | ||
| − | *The magnitude $ | + | *The magnitude $\vert H(f)\vert $ is referred to as »'''amplitude response'''« and in logarithmic form as »'''attenuation curve'''«: |
| − | :$$a(f) = - \ln | + | :$$a(f) = - \ln \vert H(f)\vert \hspace{0.2cm}{\rm in \hspace{0.1cm}Neper |
| − | \hspace{0.1cm}(Np) } = - 20 \cdot \lg | + | \hspace{0.1cm}(Np) } = - 20 \cdot \lg \vert H(f)\vert \hspace{0.2cm}{\rm in |
| − | \hspace{0.1cm} | + | \hspace{0.1cm}decibel \hspace{0.1cm}(dB) }.$$ |
| − | *The '''phase response''' $b(f)$ specifies the negative | + | *The »'''phase response'''« $b(f)$ specifies the negative $(f$–dependent$)$ angle of $H(f)$ in the complex plane with respect to the real axis: |
:$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | :$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | ||
| − | \hspace{0.1cm} | + | \hspace{0.1cm}radian \hspace{0.1cm}(rad)}.$$}} |
| + | |||
| + | |||
| − | == | + | ==Requirements for distortion-free systems== |
<br> | <br> | ||
| − | According to the explanations in the chapter [[Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions|Classification of the Distortions]] there is a distortion-free system at hand if and only if all frequency components are uniformly | + | According to the explanations in the chapter [[Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions|»Classification of the Distortions»]] there is a »distortion-free system« at hand if and only if all frequency components are uniformly attenuated and delayed: |
:$$y(t) = \alpha \cdot x(t - \tau).$$ | :$$y(t) = \alpha \cdot x(t - \tau).$$ | ||
| − | According to the laws | + | According to the systems theory laws, the following must thus hold for the frequency response: |
| − | :$$H(f) = \alpha \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f \tau}$$ | + | :$$H(f) = \alpha \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f \tau},$$ |
| − | or expressed with functions $a(f)$ and $b(f)$: | + | or expressed with the functions $a(f)$ and $b(f)$: |
*The attenuation curve must be constant for all frequencies contained in the input signal: | *The attenuation curve must be constant for all frequencies contained in the input signal: | ||
:$$a(f) = - \ln |H(f)| = - \ln \ \alpha = {\rm const.}$$ | :$$a(f) = - \ln |H(f)| = - \ln \ \alpha = {\rm const.}$$ | ||
| − | *The phase response must either be zero in the region of interest (system with no transit time) or increase linearly with frequency $(τ$ | + | *The phase response must either be zero in the region of interest $($system with no transit time$)$ or increase linearly with frequency $(τ$ indicates the transit time$)$: |
:$$b(f) = 2 \pi f \tau = {\rm const.} \cdot f.$$ | :$$b(f) = 2 \pi f \tau = {\rm const.} \cdot f.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Definitions:}$ |
| − | For a distortion-free system, both requirements must be satisfied simultaneously. Violation of even one of these two conditions results in linear distortions which are distinguished according to their cause | + | For a »'''distortion-free system'''«, both requirements must be satisfied simultaneously. |
| − | *It comes to '''attenuation distortions''' if in the frequency range of interest the attenuation curve is not constant: | + | |
| + | Violation of even one of these two conditions results in »'''linear distortions'''« which are distinguished according to their cause: | ||
| + | *It comes to »'''attenuation distortions'''« if in the frequency range of interest the attenuation curve is not constant: | ||
:$$a(f) \ne {\rm const.}$$ | :$$a(f) \ne {\rm const.}$$ | ||
| − | *In contrast to this, there are '''phase distortions''' if the phase function is not linear with respect to $f$ : | + | *In contrast to this, there are »'''phase distortions'''« if the phase function is not linear with respect to $f$ : |
:$$b(f) \ne {\rm const.} \cdot f.$$}} | :$$b(f) \ne {\rm const.} \cdot f.$$}} | ||
| − | It should be noted that in all | + | It should be noted that in all »realizable systems« – in particular, in the »minimum-phase systems« described in [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem#Attenuation_and_phase_of_minimum-phase_systems|»Chapter 3«]] – both forms of distortions usually occur simultaneously. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ In the time domain, the condition for a '''distortion-free system''' is: | + | $\text{Definition:}$ In the time domain, the condition for a »'''distortion-free system'''« is: |
:$$h(t) = \alpha \cdot \delta(t - \tau),\hspace{0.4cm}\alpha \ne 0.$$ | :$$h(t) = \alpha \cdot \delta(t - \tau),\hspace{0.4cm}\alpha \ne 0.$$ | ||
| − | Moreover, if $α = 1$ and $τ = 0$ hold,then there is an '''ideal transmission system''' | + | Moreover, if $α = 1$ and $τ = 0$ hold, then there is an »'''ideal transmission system'''«. In contrast, there are linear distortions whenever |
| − | *$h(t)$ is a continuous-time function or | + | *the impulse response $h(t)$ is a continuous-time function, or |
| − | *$h(t)$ is composed of more than one Dirac | + | |
| + | *the time-dicrete impulse response $h(t)$ is composed of more than one Dirac delta functions.}} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 1:}$ | $\text{Example 1:}$ | ||
| − | The following sketch shows the attenuation curve $a(f)$ and the phase response $b(f)$ of a distortion-free system. | + | The following sketch shows the attenuation curve $a(f)$ and the phase response $b(f)$ of a distortion-free system. |
| − | [[File:P_ID900__LZI_T_2_3_S2_neu.png|right|frame| | + | [[File:P_ID900__LZI_T_2_3_S2_neu.png|right|frame|Requirements for a non-distorting channel: <br> $f_{\rm U}$: lower $($German: "untere" ⇒ "U"$)$ range limit, <br> $f_{\rm O}$: upper $($German: "obere" ⇒ "O"$)$ range limit, <br> $f_{\rm T}$: carrier $($German: "Träger" ⇒ "T"$)$ frequency|right|class=fit]] |
| − | *In a range from $f_{\rm U}$ to $f_{\rm O}$ around the carrier frequency $f_{\rm T}$, in which the signal $x(t)$ has components, $a(f)$ is constant. | + | *In a range from $f_{\rm U}$ to $f_{\rm O}$ around the carrier frequency $f_{\rm T}$, in which the signal $x(t)$ has components, $a(f)$ is constant. |
| + | |||
*From the given constant attenuation value $6 \ \rm dB$ it follows for the amplitude response: $\vert H(f)\vert = 0.5$. | *From the given constant attenuation value $6 \ \rm dB$ it follows for the amplitude response: $\vert H(f)\vert = 0.5$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | *The output spectrum $Y(f)$ is thus half as large in magnitude as the spectral components $X(f)$ of the input signal. | ||
| + | |||
| + | *The phase response $b(f)$ increases linearly with frequency between $f_{\rm U}$ and $f_{\rm O}$. | ||
| + | |||
| + | *This results in all frequency components being delayed by the same phase delay time $τ$, where $τ$ is fixed by the slope of $b(f)$ . | ||
| + | |||
| + | *With $b(f) = 0$ a transit time-free system would arise as a result ⇒ $τ = 0$. | ||
| + | |||
| + | |||
| + | Furthermore, the following generally valid properties can be identified from the graph: | ||
| + | *The attenuation curve $a(f) = a(\hspace{-0.01cm}-\hspace{-0.08cm} f)$ is an even function in $f$. | ||
| + | |||
| + | *The phase curve $b(f) = \hspace{0.1cm}–\hspace{-0.01cm} b(\hspace{-0.01cm}-\hspace{-0.01cm}f)$ is an odd function in $f$. | ||
| + | |||
| + | |||
| + | Outside the frequency band occupied by $x(t)$ the »constant attenuation« and »linear phase« conditions do not need to be satisfied. | ||
| − | + | It can be seen from the dashed curve of $a(f)$ that even a much higher attenuation is purposeful here because as a consequence the always-existing noise components outside the useful bandwidth – which are not considered in this section – are better suppressed. }} | |
| − | == | + | ==Attenuation distortions== |
<br> | <br> | ||
| − | + | In the following, we consider the sum of two harmonic oscillations as input signal: | |
:$$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - | :$$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - | ||
\varphi_2).$$ | \varphi_2).$$ | ||
| − | + | *If the output signal can be represented in the form | |
:$$y(t) = \alpha_1 \cdot A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + \alpha_2 \cdot A_2 \cdot \cos(2 \pi f_2 \cdot t - | :$$y(t) = \alpha_1 \cdot A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + \alpha_2 \cdot A_2 \cdot \cos(2 \pi f_2 \cdot t - | ||
| − | \varphi_2) | + | \varphi_2),$$ |
| − | + | :and at the same time $α_1 ≠ α_2$ is valid, then »'''exclusively attenuation distortions'''« are existent since the phase values $\varphi_1$ and $\varphi_2$ are not changed by the system. | |
| − | + | *The attenuation constants $α_1$ and $α_2$ can be determined from the amplitude response $|H(f)|$ : | |
:$$\alpha_1 = |H(f_1)|,\hspace{0.4cm}\alpha_2 = |H(f_2)|.$$ | :$$\alpha_1 = |H(f_1)|,\hspace{0.4cm}\alpha_2 = |H(f_2)|.$$ | ||
| − | + | *If the attenuation curve $a(f)$ is given in Neper, then likewise the following holds $(1 \ \rm dB$ corresponds to $0.1151 \ \rm Np)$: | |
:$$ \alpha_1 = {\rm e}^{-{\rm a}(f_1)},\hspace{0.4cm}\alpha_2 = {\rm e}^{-{\rm a}(f_2)}.$$ | :$$ \alpha_1 = {\rm e}^{-{\rm a}(f_1)},\hspace{0.4cm}\alpha_2 = {\rm e}^{-{\rm a}(f_2)}.$$ | ||
| − | + | Please note: In some character fonts, "${\rm a}$" and "$α$" $($alpha$)$ are difficult to distinguish. | |
| − | [[File:P_ID901__LZI_T_2_3_S3_neu.png |frame| | + | {{GraueBox|TEXT= |
| − | + | [[File:P_ID901__LZI_T_2_3_S3_neu.png |frame| Effects of attenuation distortions | right|class=fit]] | |
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | The graph shows the input signal $($blue curve$)$ which is periodic with $T_0 = 1\ \rm ms$, | |
| − | :$$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$ | + | :$$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t),$$ |
| − | + | and the red curve signal $y(t)$ which is attenuation-distorted with $α_1 = 0.2$, $α_2 = 0.5$. | |
| − | + | ⇒ Significant effects of these attenuation distortions can be perceived: | |
| − | + | #$y(t)$ bears little resemblance to $x(t)$. | |
| − | + | #In contrast, considering $α_1 = α_2 = α$ the distortion-free signal $y(t) = α · x(t)$ would be obtained from which the original signal $x(t)$ could be reconstructed by amplifying it by $1/α$. | |
| − | + | We refer here explicitly to the interactive applet [[Applets:Linear_Distortions_of_Periodic_Signals|»Linear distortions of periodic signals«]]. }} | |
| − | == | + | ==Phase delay time== |
<br> | <br> | ||
| − | + | We consider a system with $|H(f)| = 1$ such that the following holds for the frequency response: | |
| − | |||
:$$H(f) = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} | :$$H(f) = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} | ||
b(f)}.$$ | b(f)}.$$ | ||
| − | * | + | *The left graph shows an exemplary phase response $b(f)$. Such a phase response is always an odd function with respect to the frequency $f$: $b(\hspace{-0.01cm}-\hspace{-0.08cm}f) = \hspace{0.08cm}-b(f)$. |
| − | * | + | |
| − | + | *On the right, the function $b(ω)$ is sketched which is dilated by a factor of $2π$ with respect to $b(f)$ in the abscissa. | |
| − | + | If the harmonic oscillation at the input is | |
| − | :$$x(t) = C \cdot \cos(2 \pi f_0 t - \varphi) | + | :$$x(t) = C \cdot \cos(2 \pi f_0 t - \varphi)\hspace{0.15cm} |
\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) = {C}/{2}\cdot | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) = {C}/{2}\cdot | ||
{\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f + f_0) | {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f + f_0) | ||
\hspace{0.01cm} + \hspace{0.01cm}{C}/{2}\cdot {\rm e}^{-{\rm | \hspace{0.01cm} + \hspace{0.01cm}{C}/{2}\cdot {\rm e}^{-{\rm | ||
| − | j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f - f_0)$$ | + | j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f - f_0),$$ |
| − | + | [[File: EN_LZI_T_2_3_S4.png|frame|On the definition of the phase delay time $\tau_{\rm P}$|class=fit]] | |
| + | |||
| + | then the following arises as a result for the spectral function at the output: | ||
:$$Y(f ) = {C}/{2}\cdot | :$$Y(f ) = {C}/{2}\cdot | ||
{\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot {\rm e}^{\hspace{0.05cm}{\rm | {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot {\rm e}^{\hspace{0.05cm}{\rm | ||
| Line 134: | Line 150: | ||
\varphi}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot | \varphi}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot | ||
\delta(f - f_0).$$ | \delta(f - f_0).$$ | ||
| − | + | Thus, the output signal is: | |
:$$y(t) = C \cdot \cos(2 \pi f_0 t - b(f_0) - \varphi).$$ | :$$y(t) = C \cdot \cos(2 \pi f_0 t - b(f_0) - \varphi).$$ | ||
| − | + | This signal can also be represented in the following form: | |
:$$y(t) = C \cdot \cos(2 \pi f_0 ( t - \tau_{\rm P}(f_0)) - \varphi).$$ | :$$y(t) = C \cdot \cos(2 \pi f_0 ( t - \tau_{\rm P}(f_0)) - \varphi).$$ | ||
| + | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The »'''phase delay time'''« indicates the delay experienced by a harmonic oscillation of frequency $f_0$ through the system. For phase-distorting systems, the phase delay time is frequency-dependent: | |
| − | :$$\tau_{\rm P}(f_0) = \frac{b(f_0)}{2\pi f_0} \hspace{0.4cm}{\rm | + | :$$\tau_{\rm P}(f_0) = \frac{b(f_0)}{2\pi f_0} \hspace{0.4cm}{\rm or} \hspace{0.4cm} |
\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}.$$}} | \tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}.$$}} | ||
| − | + | The following should be noted regarding this definition: | |
| − | *In | + | *In the $b(ω)$ representation, the phase delay time $τ_{\rm P}$ can also be determined graphically as the slope of the straight line drawn in green in the above graph. |
| − | * | + | |
| − | * | + | *In general, an oscillation with a different frequency will also result in a different phase delay time. This is the physical background for phase distortions. |
| + | |||
| + | *If for a system $b(ω) = τ_{\rm P} · ω$ or $b(f) = 2π · τ_{\rm P} · f$ is true, then all frequencies have the same phase delay time $τ_{\rm P}$. Such a system does not cause phase distortions. | ||
| − | + | We refer here again to the interactive applet [[Applets:Linear_Distortions_of_Periodic_Signals|»Linear distortions of periodic signals«]]. | |
| − | == | + | ==Difference between phase and group delay time== |
<br> | <br> | ||
| − | + | Another important system description quantity is the group delay time which must not be confused with the phase delay time. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The »'''group delay time'''« is defined as follows: | |
:$$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0}.$$ | :$$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0}.$$ | ||
| − | * | + | *This quantity is mainly used to describe narrow-band systems. |
| − | * | + | |
| + | *It indicates the delay experienced by the envelope of a band-pass system. }} | ||
| − | [[File: EN_LZI_T_2_3_S5.png| right|frame| | + | {{GraueBox|TEXT= |
| − | + | [[File: EN_LZI_T_2_3_S5.png| right|frame|On the definition of the group delay time $\tau_{\rm G}$|class=fit]] | |
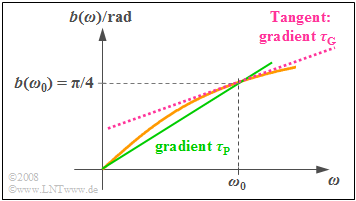
| − | $\text{ | + | $\text{Example 3:}$ |
| − | + | The graph shows the examplary phase function: | |
:$$b(ω) = \arctan (ω/ω_0).$$ | :$$b(ω) = \arctan (ω/ω_0).$$ | ||
| − | + | #This increases monotonically from zero $($at $ω = 0)$ to $π/2$ $($for $ω → ∞)$. | |
| − | + | #The function value at $ω = ω_0$ is $π/4$. | |
| − | + | If we set $ω_0 = 2π · 1 \ \rm kHz$, we obtain for the »'''phase delay time:'''« | |
:$$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz} } = {125\, \rm µ s}.$$ | :$$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz} } = {125\, \rm µ s}.$$ | ||
| − | + | ⇒ This quantity corresponds to the slope of the straight line drawn in green in the graph. | |
| − | + | In contrast, the lesser slope of the tangent line shown in red denotes the »'''group delay time:'''« | |
:$$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0} = | :$$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0} = | ||
\left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = | \left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = | ||
| Line 186: | Line 206: | ||
\approx {80\, \rm µ s}.$$}} | \approx {80\, \rm µ s}.$$}} | ||
| − | == | + | ==Phase distortions== |
<br> | <br> | ||
| − | + | To illustrate this point, we again consider the sum of two harmonic oscillations as input signal: | |
:$$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - | :$$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - | ||
\varphi_2).$$ | \varphi_2).$$ | ||
| − | + | *If the output signal for this input signal can be represented in the form | |
:$$y(t) = A_1 \cdot \cos(2 \pi f_1 \cdot (t - \tau_1) - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2) - | :$$y(t) = A_1 \cdot \cos(2 \pi f_1 \cdot (t - \tau_1) - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2) - | ||
\varphi_2)$$ | \varphi_2)$$ | ||
| − | + | :and at the same time $τ_1 ≠ τ_2$ is valid, then »'''exclusively phase distortions'''« are existent. | |
| − | + | *The two phase delay times $τ_1 ≠ τ_2$ can be determined from the phase response $($in radian$)$: | |
:$$\tau_1 = \frac{b(f_1)}{2\pi f_1} , \hspace{0.4cm}\tau_2 = \frac{b(f_2)}{2\pi | :$$\tau_1 = \frac{b(f_1)}{2\pi f_1} , \hspace{0.4cm}\tau_2 = \frac{b(f_2)}{2\pi | ||
f_2}.$$ | f_2}.$$ | ||
| − | [[File: P_ID905__LZI_T_2_3_S6_neu.png|right|frame| | + | {{GraueBox|TEXT= |
| − | + | [[File: P_ID905__LZI_T_2_3_S6_neu.png|right|frame|Effects of phase distortions|class=fit]] | |
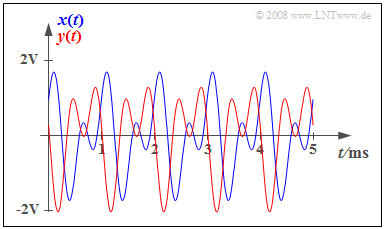
| − | $\text{ | + | $\text{Example 4:}$ |
| − | + | The graph shows the periodic signal with period $T_0$ ⇒ blue curve | |
:$$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$ | :$$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$ | ||
| − | + | as well as the signal $y(t)$ which is phase-distorted with the transit times $τ_1 = 0.7 \ \rm ms$ and $τ_2 = 0.3 \ \rm ms$ ⇒ red curve. | |
| − | * | + | *The effects of the phase distortions can be clearly seen. |
| − | * | + | *With $τ_1 = τ_2 = τ$ the following distortion-free signal would arise as a result: |
| − | :$$y(t) = x(t - τ).$$ | + | :$$y(t) = x(t - τ).$$ |
| − | + | We refer once more to the interactive applet [[Applets:Linear_Distortions_of_Periodic_Signals|»Linear distortions of periodic signals«]]. }} | |
| − | |||
| − | == | + | ==Equalization methods== |
<br> | <br> | ||
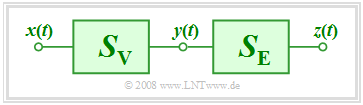
| − | [[File:P_ID906__LZI_T_2_3_S7_neu.png|right|frame| | + | [[File:P_ID906__LZI_T_2_3_S7_neu.png|right|frame|Equalization of signals|class=fit]] |
| − | + | This method, which is very important for Communications Engineering, will only be briefly touched upon here. More detailed information can be found in the books [[Modulation_Methods|»Modulation Methods«]] and [[Digital_Signal_Transmission|»Digital Signal Transmission«]]. | |
| − | + | ||
| − | + | For this brief description, we assume the outlined constellation: | |
| − | *$S_{\rm V}$ | + | *$S_{\rm V}$ denotes a distorting system, because of »distortion« ⇒ German: "Verzerrung" ⇒ "V". |
| − | + | ||
| + | *$S_{\rm E}$ serves for equalization ⇒ "E". | ||
| − | + | Regarding this constellation, the following should be noted: | |
| − | + | #If the distortion is nonlinear, the equalization must also be nonlinear. | |
| − | + | #But even with linear distortion, nonlinear equalization methods are used, e.g. »Decision Feedback Equalisation« $\rm (DFE)$ in digital systems. <br>The advantage over linear equalization is that there is no increase in noise power. | |
| − | + | #If $S_{\rm V}$ is a linear system with frequency response $H_{\rm V}(f)$, <br>then the distortions can be completely eliminated with the »'''inverse frequency response'''« $H_{\rm E}(f) = 1/H_{\rm V}(f)$ and $z(t) = x(t)$ holds. | |
| − | + | #A prerequisite for this is that the frequency response $H_{\rm V}(f)$ has no zeros in the spectral range of interest, as otherwise $H_{\rm E}(f)$ would result in infinity points. | |
| − | + | #For »analog systems«, complete equalization means that $z(t)$ differs from $x(t)$ only by the unavoidable noise components and possibly by a transit time. | |
| − | + | #For »digital systems«, the complete equalization criterion is less strict. It must then only be ensured that the signals $x(t)$ and $z(t)$ coincide at the detection times. | |
| + | #In this context, one deals with [[Digital_Signal_Transmission/Eigenschaften_von_Nyquistsystemen|»'''Nyquist systems'''«]]. | ||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.5:_Distortion_and_Equalization|Exercise 2.5: Distortion and Equalization]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.5Z:_Nyquist_Equalization|Exercise 2.5Z: Nyquist Equalization]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.6:_Two-Way_Channel|Exercise 2.6: Two-Way Channel]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.6Z:_Synchronous_Demodulator|Exercise 2.6Z: Synchronous Demodulator]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.7:_Two-Way_Channel_once_more|Exercise 2.7: Two-Way Channel once more]] |
{{Display}} | {{Display}} | ||
Latest revision as of 18:47, 14 November 2023
Contents
Compilation of important descriptive quantities
Now nonlinear distortions are excluded so that the system is fully described by the frequency response $H(f)$ .
$\text{System model:}$ The »generally complex frequency response« can also be formulated as follows:
- $$H(f) = \vert H(f) \vert \cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)} = {\rm e}^{- a(f)}\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
This yields the following descriptive quantities:
- The magnitude $\vert H(f)\vert $ is referred to as »amplitude response« and in logarithmic form as »attenuation curve«:
- $$a(f) = - \ln \vert H(f)\vert \hspace{0.2cm}{\rm in \hspace{0.1cm}Neper \hspace{0.1cm}(Np) } = - 20 \cdot \lg \vert H(f)\vert \hspace{0.2cm}{\rm in \hspace{0.1cm}decibel \hspace{0.1cm}(dB) }.$$
- The »phase response« $b(f)$ specifies the negative $(f$–dependent$)$ angle of $H(f)$ in the complex plane with respect to the real axis:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in \hspace{0.1cm}radian \hspace{0.1cm}(rad)}.$$
Requirements for distortion-free systems
According to the explanations in the chapter »Classification of the Distortions» there is a »distortion-free system« at hand if and only if all frequency components are uniformly attenuated and delayed:
- $$y(t) = \alpha \cdot x(t - \tau).$$
According to the systems theory laws, the following must thus hold for the frequency response:
- $$H(f) = \alpha \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f \tau},$$
or expressed with the functions $a(f)$ and $b(f)$:
- The attenuation curve must be constant for all frequencies contained in the input signal:
- $$a(f) = - \ln |H(f)| = - \ln \ \alpha = {\rm const.}$$
- The phase response must either be zero in the region of interest $($system with no transit time$)$ or increase linearly with frequency $(τ$ indicates the transit time$)$:
- $$b(f) = 2 \pi f \tau = {\rm const.} \cdot f.$$
$\text{Definitions:}$ For a »distortion-free system«, both requirements must be satisfied simultaneously.
Violation of even one of these two conditions results in »linear distortions« which are distinguished according to their cause:
- It comes to »attenuation distortions« if in the frequency range of interest the attenuation curve is not constant:
- $$a(f) \ne {\rm const.}$$
- In contrast to this, there are »phase distortions« if the phase function is not linear with respect to $f$ :
- $$b(f) \ne {\rm const.} \cdot f.$$
It should be noted that in all »realizable systems« – in particular, in the »minimum-phase systems« described in »Chapter 3« – both forms of distortions usually occur simultaneously.
$\text{Definition:}$ In the time domain, the condition for a »distortion-free system« is:
- $$h(t) = \alpha \cdot \delta(t - \tau),\hspace{0.4cm}\alpha \ne 0.$$
Moreover, if $α = 1$ and $τ = 0$ hold, then there is an »ideal transmission system«. In contrast, there are linear distortions whenever
- the impulse response $h(t)$ is a continuous-time function, or
- the time-dicrete impulse response $h(t)$ is composed of more than one Dirac delta functions.
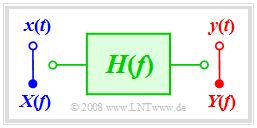
$\text{Example 1:}$ The following sketch shows the attenuation curve $a(f)$ and the phase response $b(f)$ of a distortion-free system.
- In a range from $f_{\rm U}$ to $f_{\rm O}$ around the carrier frequency $f_{\rm T}$, in which the signal $x(t)$ has components, $a(f)$ is constant.
- From the given constant attenuation value $6 \ \rm dB$ it follows for the amplitude response: $\vert H(f)\vert = 0.5$.
- The output spectrum $Y(f)$ is thus half as large in magnitude as the spectral components $X(f)$ of the input signal.
- The phase response $b(f)$ increases linearly with frequency between $f_{\rm U}$ and $f_{\rm O}$.
- This results in all frequency components being delayed by the same phase delay time $τ$, where $τ$ is fixed by the slope of $b(f)$ .
- With $b(f) = 0$ a transit time-free system would arise as a result ⇒ $τ = 0$.
Furthermore, the following generally valid properties can be identified from the graph:
- The attenuation curve $a(f) = a(\hspace{-0.01cm}-\hspace{-0.08cm} f)$ is an even function in $f$.
- The phase curve $b(f) = \hspace{0.1cm}–\hspace{-0.01cm} b(\hspace{-0.01cm}-\hspace{-0.01cm}f)$ is an odd function in $f$.
Outside the frequency band occupied by $x(t)$ the »constant attenuation« and »linear phase« conditions do not need to be satisfied.
It can be seen from the dashed curve of $a(f)$ that even a much higher attenuation is purposeful here because as a consequence the always-existing noise components outside the useful bandwidth – which are not considered in this section – are better suppressed.
Attenuation distortions
In the following, we consider the sum of two harmonic oscillations as input signal:
- $$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2).$$
- If the output signal can be represented in the form
- $$y(t) = \alpha_1 \cdot A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + \alpha_2 \cdot A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2),$$
- and at the same time $α_1 ≠ α_2$ is valid, then »exclusively attenuation distortions« are existent since the phase values $\varphi_1$ and $\varphi_2$ are not changed by the system.
- The attenuation constants $α_1$ and $α_2$ can be determined from the amplitude response $|H(f)|$ :
- $$\alpha_1 = |H(f_1)|,\hspace{0.4cm}\alpha_2 = |H(f_2)|.$$
- If the attenuation curve $a(f)$ is given in Neper, then likewise the following holds $(1 \ \rm dB$ corresponds to $0.1151 \ \rm Np)$:
- $$ \alpha_1 = {\rm e}^{-{\rm a}(f_1)},\hspace{0.4cm}\alpha_2 = {\rm e}^{-{\rm a}(f_2)}.$$
Please note: In some character fonts, "${\rm a}$" and "$α$" $($alpha$)$ are difficult to distinguish.
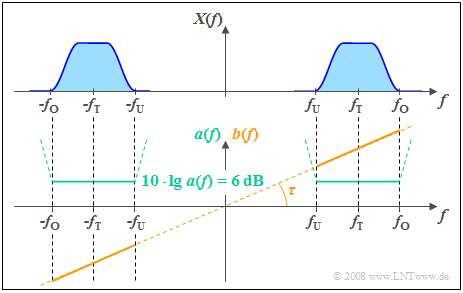
$\text{Example 2:}$ The graph shows the input signal $($blue curve$)$ which is periodic with $T_0 = 1\ \rm ms$,
- $$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t),$$
and the red curve signal $y(t)$ which is attenuation-distorted with $α_1 = 0.2$, $α_2 = 0.5$.
⇒ Significant effects of these attenuation distortions can be perceived:
- $y(t)$ bears little resemblance to $x(t)$.
- In contrast, considering $α_1 = α_2 = α$ the distortion-free signal $y(t) = α · x(t)$ would be obtained from which the original signal $x(t)$ could be reconstructed by amplifying it by $1/α$.
We refer here explicitly to the interactive applet »Linear distortions of periodic signals«.
Phase delay time
We consider a system with $|H(f)| = 1$ such that the following holds for the frequency response:
- $$H(f) = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
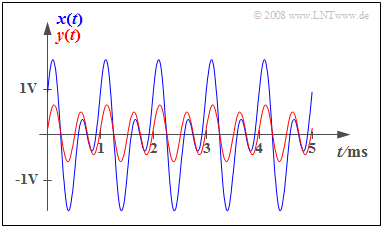
- The left graph shows an exemplary phase response $b(f)$. Such a phase response is always an odd function with respect to the frequency $f$: $b(\hspace{-0.01cm}-\hspace{-0.08cm}f) = \hspace{0.08cm}-b(f)$.
- On the right, the function $b(ω)$ is sketched which is dilated by a factor of $2π$ with respect to $b(f)$ in the abscissa.
If the harmonic oscillation at the input is
- $$x(t) = C \cdot \cos(2 \pi f_0 t - \varphi)\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) = {C}/{2}\cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f + f_0) \hspace{0.01cm} + \hspace{0.01cm}{C}/{2}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f - f_0),$$
then the following arises as a result for the spectral function at the output:
- $$Y(f ) = {C}/{2}\cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot \delta(f + f_0) \hspace{0.05cm} + \hspace{0.05cm}{C}/{2}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot \delta(f - f_0).$$
Thus, the output signal is:
- $$y(t) = C \cdot \cos(2 \pi f_0 t - b(f_0) - \varphi).$$
This signal can also be represented in the following form:
- $$y(t) = C \cdot \cos(2 \pi f_0 ( t - \tau_{\rm P}(f_0)) - \varphi).$$
$\text{Definition:}$ The »phase delay time« indicates the delay experienced by a harmonic oscillation of frequency $f_0$ through the system. For phase-distorting systems, the phase delay time is frequency-dependent:
- $$\tau_{\rm P}(f_0) = \frac{b(f_0)}{2\pi f_0} \hspace{0.4cm}{\rm or} \hspace{0.4cm} \tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}.$$
The following should be noted regarding this definition:
- In the $b(ω)$ representation, the phase delay time $τ_{\rm P}$ can also be determined graphically as the slope of the straight line drawn in green in the above graph.
- In general, an oscillation with a different frequency will also result in a different phase delay time. This is the physical background for phase distortions.
- If for a system $b(ω) = τ_{\rm P} · ω$ or $b(f) = 2π · τ_{\rm P} · f$ is true, then all frequencies have the same phase delay time $τ_{\rm P}$. Such a system does not cause phase distortions.
We refer here again to the interactive applet »Linear distortions of periodic signals«.
Difference between phase and group delay time
Another important system description quantity is the group delay time which must not be confused with the phase delay time.
$\text{Definition:}$ The »group delay time« is defined as follows:
- $$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0}.$$
- This quantity is mainly used to describe narrow-band systems.
- It indicates the delay experienced by the envelope of a band-pass system.
$\text{Example 3:}$ The graph shows the examplary phase function:
- $$b(ω) = \arctan (ω/ω_0).$$
- This increases monotonically from zero $($at $ω = 0)$ to $π/2$ $($for $ω → ∞)$.
- The function value at $ω = ω_0$ is $π/4$.
If we set $ω_0 = 2π · 1 \ \rm kHz$, we obtain for the »phase delay time:«
- $$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz} } = {125\, \rm µ s}.$$
⇒ This quantity corresponds to the slope of the straight line drawn in green in the graph.
In contrast, the lesser slope of the tangent line shown in red denotes the »group delay time:«
- $$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0} = \left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = \omega_0} = \frac{1}{2\omega_0}= \frac{1}{4 \pi \cdot{1\, \rm kHz} } \approx {80\, \rm µ s}.$$
Phase distortions
To illustrate this point, we again consider the sum of two harmonic oscillations as input signal:
- $$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2).$$
- If the output signal for this input signal can be represented in the form
- $$y(t) = A_1 \cdot \cos(2 \pi f_1 \cdot (t - \tau_1) - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2) - \varphi_2)$$
- and at the same time $τ_1 ≠ τ_2$ is valid, then »exclusively phase distortions« are existent.
- The two phase delay times $τ_1 ≠ τ_2$ can be determined from the phase response $($in radian$)$:
- $$\tau_1 = \frac{b(f_1)}{2\pi f_1} , \hspace{0.4cm}\tau_2 = \frac{b(f_2)}{2\pi f_2}.$$
$\text{Example 4:}$ The graph shows the periodic signal with period $T_0$ ⇒ blue curve
- $$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$
as well as the signal $y(t)$ which is phase-distorted with the transit times $τ_1 = 0.7 \ \rm ms$ and $τ_2 = 0.3 \ \rm ms$ ⇒ red curve.
- The effects of the phase distortions can be clearly seen.
- With $τ_1 = τ_2 = τ$ the following distortion-free signal would arise as a result:
- $$y(t) = x(t - τ).$$
We refer once more to the interactive applet »Linear distortions of periodic signals«.
Equalization methods
This method, which is very important for Communications Engineering, will only be briefly touched upon here. More detailed information can be found in the books »Modulation Methods« and »Digital Signal Transmission«.
For this brief description, we assume the outlined constellation:
- $S_{\rm V}$ denotes a distorting system, because of »distortion« ⇒ German: "Verzerrung" ⇒ "V".
- $S_{\rm E}$ serves for equalization ⇒ "E".
Regarding this constellation, the following should be noted:
- If the distortion is nonlinear, the equalization must also be nonlinear.
- But even with linear distortion, nonlinear equalization methods are used, e.g. »Decision Feedback Equalisation« $\rm (DFE)$ in digital systems.
The advantage over linear equalization is that there is no increase in noise power. - If $S_{\rm V}$ is a linear system with frequency response $H_{\rm V}(f)$,
then the distortions can be completely eliminated with the »inverse frequency response« $H_{\rm E}(f) = 1/H_{\rm V}(f)$ and $z(t) = x(t)$ holds. - A prerequisite for this is that the frequency response $H_{\rm V}(f)$ has no zeros in the spectral range of interest, as otherwise $H_{\rm E}(f)$ would result in infinity points.
- For »analog systems«, complete equalization means that $z(t)$ differs from $x(t)$ only by the unavoidable noise components and possibly by a transit time.
- For »digital systems«, the complete equalization criterion is less strict. It must then only be ensured that the signals $x(t)$ and $z(t)$ coincide at the detection times.
- In this context, one deals with »Nyquist systems«.
Exercises for the chapter
Exercise 2.5: Distortion and Equalization
Exercise 2.5Z: Nyquist Equalization
Exercise 2.6Z: Synchronous Demodulator
Exercise 2.7: Two-Way Channel once more