Difference between revisions of "Linear and Time Invariant Systems/Inverse Laplace Transform"

Revision as of 23:19, 12 October 2021

Problem formulation and prerequisites

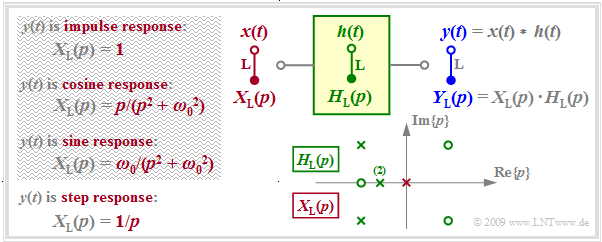
$\text{Statement of task:}$ This chapter deals with the following problem:

The $p$–spectral function $Y_{\rm L}(p)$ in pole-zero notation is known.
The inverse Laplace transform, i.e. the associated time function $y(t)$ is searched-for, where the following notation should hold:

$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm briefly}\hspace{0.3cm} y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$

The graph summarizes the prerequisites for this task.

Prerequisites for the chapter "Inverse Laplace Transform"

$H_{\rm L}(p)$ describes the causal transmission system and $Y_{\rm L}(p)$ specifies the Laplace transform of the output signal $y(t)$ considering the input signal $x(t)$ . $Y_{\rm L}(p)$ is characterized by $N$ poles, by $Z ≤ N$ zeros and by the constant $K.$
The poles and zeros exhibit the properties mentioned in the last chapter : Poles are only allowed to lie in the left $p$–half plane or on the imaginary axis, whereas zeros are also allowed in the right $p$–half plane.
All singularities – this is the generic term for poles and zeros – are either real or exist as pairs of conjugate-complex singularities. Multiple poles and zeros are also allowed.
Using the input signal $x(t) = δ(t) \ \ ⇒ \ \ X_{\rm L}(p) = 1 \ \ ⇒ \ \ Y_{\rm L}(p) = H_{\rm L}(p)$, the output signal $y(t)$ then describes the impulse response $h(t)$ des Übertragungssystems. Zur Berechnung dürfen hierfür nur die in der Grafik grün eingezeichneten Singularitäten herangezogen werden.
Eine Sprungfunktion $x(t) = γ(t) \ \ ⇒ \ \ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der Sprungantwort $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p = 0$ zu berücksichtigen.
Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rm L}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe Tabelle im Kapitel "Laplace–Transformation und $p$–Übertragungsfunktion"), zum Beispiel ein zum Zeitpunkt $t = 0$ eingeschaltetes Cosinus– oder Sinussignal.
Bei der hier beschriebenen Vorgehensweise ist also ein Rechteck als Eingangssignal $x(t)\ \ ⇒ \ \ X_{\rm L}(p) = (1 - {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot \hspace{0.05cm} T})/p$ nicht möglich. Die Rechteckantwort $y(t)$ kann aber als Differenz zweier Sprungantworten indirekt berechnet werden.

Some results of the theory of functions

Im Gegensatz zu den Fourierintegralen, die sich in den beiden Transformationsrichtungen nur geringfügig unterscheiden, ist bei "Laplace" die Berechnung von $y(t)$ aus $Y_{\rm L}(p)$ – also die Rücktransformation –

sehr viel schwieriger als die Berechnung von $Y_{\rm L}(p)$ aus $y(t)$,
auf elementarem Weg nicht oder nur sehr umständlich lösbar.

$\text{Definition:}$ Allgemein gilt für die Laplace–Rücktransformation:

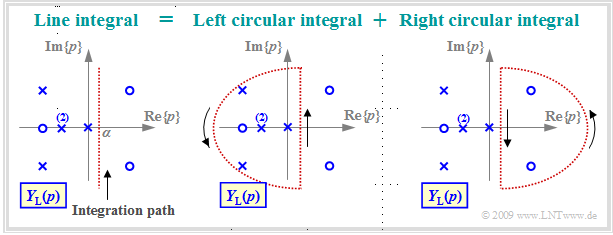
$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}= \lim_{\beta \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} \hspace{0.15cm} \frac{1}{ {\rm j} \cdot 2 \pi}\cdot \int_{ \alpha - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta } ^{\alpha+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta} Y_{\rm L}(p) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm}{\rm d}p \hspace{0.05cm} .$$

Die Integration erfolgt parallel zur imaginären Achse.
Der Realteil $α$ ist so zu wählen, dass alle Pole links vom Integrationsweg liegen.

Linienintegral sowie linkes und rechtes Kreisintegral

Die linke Grafik verdeutlicht dieses Linienintegral entlang der rot gepunkteten Vertikalen ${\rm Re}\{p\}= α$. Lösbar ist dieses Integral mit dem Jordanschen Lemma der Funktionstheorie. In diesem Tutorial folgt nur eine sehr kurze und einfache Zusammenfassung der Vorgehensweise:

Das Linienintegral kann entsprechend der Skizze in zwei Kreisintegrale aufgeteilt werden, wobei sämtliche Polstellen im linken Kreisintegral liegen, während das rechte Kreisintegral nur Nullstellen beinhalten darf.
Entsprechend der Funktionstheorie liefert das rechte Kreisintegral die Zeitfunktion $y(t)$ für negative Zeiten. Aufgrund der Kausalität muss $y(t < 0)$ identisch Null sein, was aber nach dem Hauptsatz der Funktionstheorie nur dann zutrifft, wenn es in der rechten $p$–Halbebene keine Pole gibt.
Das Integral über den linken Halbkreis liefert dagegen die Zeitfunktion für $t ≥ 0$. Dieses umschließt alle Polstellen und ist mit dem Residuensatz in (relativ) einfacher Weise berechenbar, wie auf den nächsten Seiten gezeigt wird.

Formulation of the residue theorem

Es wird weiter vorausgesetzt, dass die Übertragungsfunktion $Y_{\rm L}(p)$ in Pol–Nullstellen–Form durch

den konstanten Faktor $K$,
die $Z$ Nullstellen $p_{{\rm o}i}$ $(i = 1$, ... , $Z)$ und
die $N$ Polstellen $p_{{\rm x}i}$ $(i = 1$, ... , $N$)

dargestellt werden kann. Wir setzen zudem $Z < N$ voraus.

Die Anzahl der unterscheidbaren Pole bezeichnen wir mit $I$. Zur Bestimung von $I$ werden mehrfache Pole nur einfach gezählt. So gilt für die Skizze im letzten Abschnitt unter Berücksichtigung des Poles bei $p=0$ aufgrund der doppelten Polstelle: $N = 5$ und $I = 4$.

$\text{Residuensatz:}$ Unter den genannten Voraussetzungen ergibt sich die Laplace–Rücktransformierte von $Y_{\rm L}(p)$ für Zeiten $t ≥ 0$ als die Summe von $I$ Eigenschwingungen der Pole, die man als die Residuen – abgekürzt mit „Res” – bezeichnet:

$$y(t) = \sum_{i=1}^{I}{\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}_i}} \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p \hspace{0.05cm}t}\} \hspace{0.05cm} .$$

Da $Y_{\rm L}(p)$ nur für kausale Signale angebbar ist, gilt für negative Zeiten stets $y(t < 0) = 0$.

Für einen Pol der Vielfachheit $l$ gilt allgemein:

$${\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{1}{(l-1)!}\cdot \frac{ {\rm d}^{\hspace{0.05cm}l-1} }{ {\rm d}p^{\hspace{0.05cm}l-1} }\hspace{0.15cm} \left \{Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i})^{\hspace{0.05cm}l}\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg \vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$

Als Sonderfall ergibt sich daraus mit $l = 1$ für einen einfachen Pol:

$${\rm Res} \bigg\vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i} )\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$

Auf den nächsten Seiten wird der Residuensatz anhand dreier ausführlicher Beispiele verdeutlicht, die mit den drei Konstellationen im $\text{Beispiel 3}$ im Kapitel "Laplace–Transformation" korrespondieren:

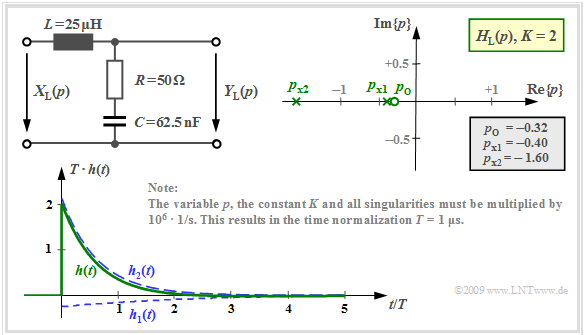
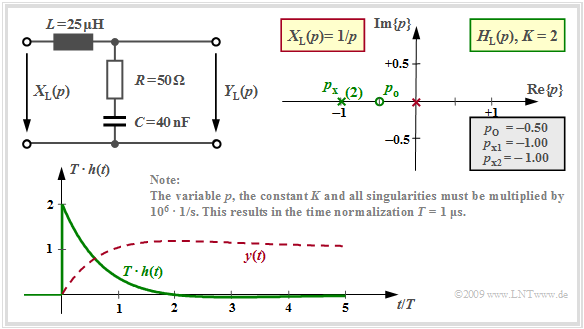
Wir betrachten also wieder den Vierpol mit einer Induktivität $L = 25 \ \rm µH$ im Längszweig sowie im Querzweig die Serienschaltung aus einem Ohmschen Widerstand $R = 50 \ \rm Ω$ und einer Kapazität $C$.
Für Letztere betrachten wir wieder drei verschiedene Werte, nämlich $C = 62.5 \ \rm nF$, $C = 8 \ \rm nF$ und $C = 40 \ \rm nF$.
Vorausgesetzt ist stets $x(t) = δ(t) \; ⇒ \; X_{\rm L}(p) = 1$ ⇒ $Y_{\rm L}(p) = H_{\rm L}(p)$ ⇒ $y(t)$ ist gleich der Impulsantwort $h(t)$.

Aperiodically decaying impulse response

Mit der Kapazität $C = 62.5 \ \rm nF$ und den weiteren in der unteren Grafik angegebenen Zahlenwerten erhält man für die auf der Seite Pol–Nullstellen–Darstellung von Schaltungen berechnete $p$–Übertragungsfunktion:

$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})}= 2 \cdot \frac {p + 0.32 } {(p +0.4)(p +1.6 )} \hspace{0.05cm} .$$

Beachten Sie bitte die Normierung von $p$, $K$ sowie aller Pole und Nullstellen mit dem Faktor ${\rm 10^6} · 1/\rm s$.

Die Impulsantwort setzt sich aus $I = N = 2$ Eigenschwingungen zusammen. Für $t < 0$ sind diese gleich Null.

Das Residium des Pols bei $p_{{\rm x}1} =\ –0.4$ liefert die folgende Zeitfunktion:

$$h_1(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}1})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}=2 \cdot \frac {p + 0.32 } {p +0.4}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.4}= - \frac {2 } {15}\cdot {\rm e}^{-0.4 \hspace{0.05cm} t} \hspace{0.05cm}. $$

In gleicher Weise kann das Residium des zweiten Pols bei $p_{{\rm x}2} = \ –1.6$ berechnet werden:

$$h_2(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}2})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}}=2 \cdot \frac {p + 0.32 } {p +1.6}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1.6}= \frac {32 } {15}\cdot {\rm e}^{-1.6 \hspace{0.05cm} t} \hspace{0.05cm}. $$

Abklingende Impulsantwort

Die Grafik zeigt $h_1(t)$ und $h_2(t)$ sowie das Summensignal $h(t)$.

Berücksichtigt ist auch hier der Normierungsfaktor $1/T = 10^6 · \rm 1/s$, so dass die Zeit auf $T = 1 \ \rm µ s$ normiert ist.
Für $t =0$ ergibt sich $T \cdot h(t=0) = {32 }/ {15} -{2 }/ {15}= 2 \hspace{0.05cm}$.
Für Zeiten $t > 2 \ \rm µ s$ ist die Impulsantwort negativ
(wenn auch nur geringfügig und in der Grafik nur schwer zu erkennen).

Attenuated-oscillatory impulse response

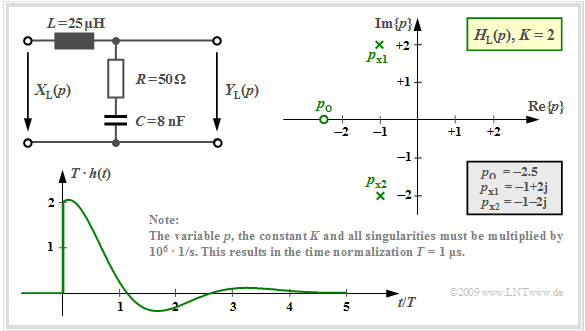
Die Bauelementewerte $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 8 \ \rm nF$ ergeben zwei konjugiert komplexe Pole bei $p_{{\rm x}1} = \ –1 + {\rm j} · 2$ und $p_{{\rm x}2} = \ –1 - {\rm j} · 2$. Die Nullstelle liegt bei $p_{\rm o} = \ –2.5$. Es gilt $K = 2$ und alle Zahlenwerte sind wieder mit dem Faktor $1/T$ zu multiplizieren $(T = 1\ \rm µ s$).

Wendet man den Residuensatz auf diese Konfiguration an, so erhält man:

$$h_1(t) = \text{ ...} = K \cdot \frac {p_{\rm x 1} - p_{\rm o }} {p_{\rm x 1} - p_{\rm x 2}}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot \hspace{0.05cm}t}= 2 \cdot \frac {-1 + {\rm j}\cdot 2 +2.5} {(-1 + {\rm j}\cdot 2) - (-1 - {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}= 2 \cdot \frac {1.5 + {\rm j}\cdot 2} {{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}$$

$$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {1.5 + {\rm j}\cdot 2} {{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}= (1 - {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} ,$$

$$ h_2(t) = \text{ ...} = K \cdot \frac {p_{\rm x 2} - p_{\rm o }} {p_{\rm x 2} - p_{\rm x 1}}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot \hspace{0.05cm}t}= 2 \cdot \frac {-1 - {\rm j}\cdot 2 +2.5} {(-1 - {\rm j}\cdot 2) - (-1 + {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t}=2 \cdot \frac {1.5 - {\rm j}\cdot 2} {-{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t} $$

Gedämpft oszillierende Impulsantwort

$$\Rightarrow \hspace{0.3cm}h_2(t) = (1 + {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} . $$

Mit dem Satz von Euler ergibt sich somit für das Summensignal:

$$h(t) = h_1(t) + h_2(t)$$

$$\Rightarrow \hspace{0.3cm}h(t) = {\rm e}^{-t}\cdot \big [ (1 - {\rm j}\cdot 0.75)\cdot (\cos() + {\rm j}\cdot \sin())+ $$

$$\hspace{3.1cm}+ (1 + {\rm j}\cdot 0.75)\cdot (\cos() - {\rm j}\cdot \sin())\big ]$$

$$\Rightarrow \hspace{0.3cm}h(t) ={\rm e}^{-t}\cdot \big [ 2\cdot \cos(2t) + 1.5 \cdot \sin(2t)\big ]\hspace{0.05cm} . $$

Die Grafik zeigt die nun mit ${\rm e}^{–t}$ gedämpft oszillierende Impulsantwort $h(t)$ für diese Pol–Nullstellen–Konfiguration.

Critically-damped case

Mit $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 40 \ \rm nF$ ergibt sich der so genannte aperiodische Grenzfall:

$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x })^2}= 2 \cdot \frac {p + 0.5 } {(p +1)^2} \hspace{0.05cm} .$$

Der Kapazitätswert $C = 40 \ \rm nF$ ist der kleinstmögliche Wert, für den sich gerade noch reelle Polstellen ergeben. Diese fallen zusammen, das heißt $p_{\rm x} = \ –1$ ist eine doppelte Polstelle. Die Zeitfunktion lautet somit entsprechend dem Residuensatz mit $l = 2$:

$$h(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm} \left \{H_{\rm L}(p)\cdot (p - p_{ {\rm x} })^2\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } = K \cdot \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm}\left \{ (p - p_{ {\rm o} })\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{0.05cm} .$$

Mit der Produktregel der Differentialrechnung ergibt sich daraus:

Impulsantwort und Sprungantwort des aperiodischen Grenzfalls

$$h(t) = K \cdot \left [ {\rm e}^{p \hspace{0.05cm}t} + (p - p_{ {\rm o} })\cdot t \cdot {\rm e}^{p \hspace{0.05cm}t} \right ] \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1} = {\rm e}^{-t}\cdot \left ( 2 - t \right) \hspace{0.05cm} .$$

Die Grafik zeigt diese Impulsantwort (grüne Kurve) in normierter Darstellung. Sie unterscheidet sich von derjenigen mit den beiden unterschiedlichen Polen bei $-0.4$ und $-1.6$ nur geringfügig.

Das rot gezeichnete Signal $y(t) = 1 - {\rm e}^{-t} + t \cdot {\rm e}^{-t}$ ergibt sich, wenn man am Eingang zusätzlich eine Sprungfunktion berücksichtigt ⇒ Sprungantwort.

Zur Berechnung der Sprungantwort $\sigma(t) = y(t)$ kann man alternativ

bei der Residuenberechnung einen zusätzlichen Pol bei $p = 0$ (rot markiert) berücksichtigen,
oder das Integral über die Impulsantwort $h(t)$ bilden.

Partial fraction decomposition

Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt ⇒ $Z$ muss stets kleiner als $N$ sein.

Gilt dagegen wie bei einem Hochpass $Z = N$, so

ist der Grenzwert der Spektralfunktion für großes $p$ ungleich Null,
beinhaltet das zugehörige Zeitsignal $y(t)$ auch einen Diracimpuls,
versagt der Residuensatz und es ist eine Partialbruchzerlegung vorzunehmen.

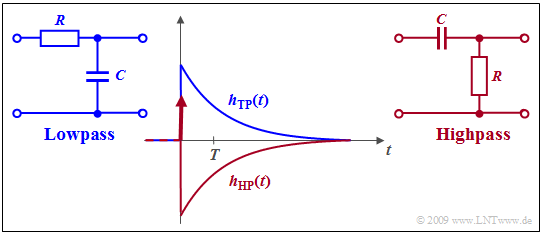
Die Vorgehensweise soll beispielhaft für einen Hochpass erster Ordnung verdeutlicht werden.

Impulsantwort von Tiefpass (blau) und Hochpass (rot)

$\text{Beispiel 1:}$ Die $p$–Übertragungsfunktion eines $RC$–Hochpasses erster Ordnung kann durch Abspaltung einer Konstanten wie folgt umgewandelt werden:

$$\frac{p}{p + RC} = 1- \frac{RC}{p + RC}\hspace{0.05cm} .$$

Damit lautet die Hochpass–Impulsantwort:

$$h_{\rm HP}(t) = \delta(t) - h_{\rm TP}(t) \hspace{0.05cm} .$$

Die Grafik zeigt

als rote Kurve die Hochpass–Impulsantwort $h_{\rm HP}(t)$,
als blaue Kurve die Impulsantwort $h_{\rm TP}(t)$ des äquivalenten Tiefpasses.

Die Diracfunktion ist die Laplace–Transformierte des konstanten Wertes $1$, während die zweite Funktion die Impulsantwort des äquivalenten Tiefpasses angibt, die mit $Z = 0$, $N =1$ und $K = RC$ durch den Residuensatz angebbar ist.

Exercises for the chapter

Exercise 3.5: Circuit with R, L and C

Exercise 3.5Z: Application of the Residue Theorem

Exercise 3.6: Transient Behaviour

Exercise 3.6Z: Two Imaginary Poles

Exercise 3.7: Impulse Response of a High-Pass Filter

Exercise 3.7Z: Partial Fraction Decomposition

@@ Line 22: / Line 22: @@
 *The poles and zeros exhibit the properties mentioned in the&nbsp; [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function#Properties_of_poles_and_zeros|last chapter]]&nbsp;: &nbsp; Poles are only allowed to lie in the left &nbsp;$p$–half plane or on the imaginary axis, whereas zeros are also allowed in the right &nbsp;$p$–half plane.
 *All singularities – this is the generic term for poles and zeros – are either real or exist as pairs of conjugate-complex singularities.&nbsp; Multiple poles and zeros are also allowed.
-*Using the input signal &nbsp;$x(t) = δ(t) \ \  ⇒ \ \  X_{\rm L}(p) = 1  \ \  ⇒  \ \  Y_{\rm L}(p) = H_{\rm L}(p)$, then the output signal &nbsp;$y(t)$&nbsp; describes the [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Impulse_response|impulse response]]  &nbsp;$h(t)$&nbsp; des Übertragungssystems.&nbsp; Zur Berechnung dürfen hierfür nur die in der Grafik grün eingezeichneten Singularitäten herangezogen werden.
+*Using the input signal &nbsp;$x(t) = δ(t) \ \  ⇒ \ \  X_{\rm L}(p) = 1  \ \  ⇒  \ \  Y_{\rm L}(p) = H_{\rm L}(p)$, the output signal &nbsp;$y(t)$&nbsp; then describes the [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Impulse_response|impulse response]]  &nbsp;$h(t)$&nbsp; des Übertragungssystems.&nbsp; Zur Berechnung dürfen hierfür nur die in der Grafik grün eingezeichneten Singularitäten herangezogen werden.
 *Eine Sprungfunktion &nbsp;$x(t) = γ(t) \ \  ⇒ \ \  X_{\rm L} = 1/p$&nbsp; am Eingang bewirkt, dass das Ausgangssignal &nbsp;$y(t)$&nbsp; gleich der &nbsp;[[Linear_and_Time_Invariant_Systems/Systembeschreibung_im_Zeitbereich#Sprungantwort|Sprungantwort]] &nbsp; $σ(t)$ von $H_{\rm L}(p)$&nbsp; ist.&nbsp; Zur Berechnung ist neben den Singularitäten von &nbsp;$H_{\rm L}(p)$&nbsp; nun auch die (in der Grafik rot eingezeichnete) Polstelle bei &nbsp;$p = 0$&nbsp; zu berücksichtigen.
 *Als Eingang &nbsp;$x(t)$&nbsp; sind nur Signale möglich, für die &nbsp;$X_{ \rm L}(p)$&nbsp; in Pol–Nullstellen–Form darstellbar ist &nbsp; (siehe &nbsp;[[Linear_and_Time_Invariant_Systems/Laplace–Transformation_und_p–Übertragungsfunktion#Einige_wichtige_Laplace.E2.80.93Korrespondenzen|Tabelle]]&nbsp;  im Kapitel "Laplace–Transformation und $p$–Übertragungsfunktion"), zum Beispiel ein zum Zeitpunkt &nbsp;$t = 0$&nbsp; eingeschaltetes Cosinus– oder Sinussignal.