Inverse Laplace Transform

Problem formulation and prerequisites

$\text{Task:}$ This chapter deals with the following problem:

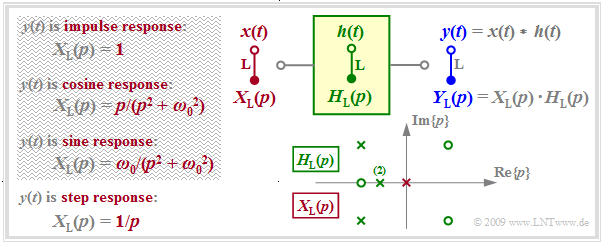
The $p$–spectral function $Y_{\rm L}(p)$ is given in "pole-zero" notation.
The inverse Laplace transform, i.e. the associated time function $y(t)$ is searched-for, where the following notation should hold:

$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm briefly}\hspace{0.3cm} y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$

Prerequisites for the chapter "Inverse Laplace Transform"

The graph summarizes the prerequisites for this task.

$H_{\rm L}(p)$ describes the transfer function of the causal system and $Y_{\rm L}(p)$ specifies the Laplace transform of the output signal $y(t)$ considering the input signal $x(t)$ . $Y_{\rm L}(p)$ is characterized by $N$ poles, by $Z ≤ N$ zeros and by the constant $K.$
Poles and zeros exhibit the properties mentioned in the last chapter: Poles are only allowed in the left $p$–half plane or on the imaginary axis; zeros are also allowed in the right $p$–half plane.
All singularities – this is the generic term for poles and zeros – are either real or exist as pairs of conjugate-complex singularities. Multiple poles and zeros are also allowed.
With the input $x(t) = δ(t)$ ⇒ $X_{\rm L}(p) = 1$ ⇒ $Y_{\rm L}(p) = H_{\rm L}(p)$, the output signal $y(t)$ then describes the impulse response $h(t)$ of the transmission system. For this purpose, only the singularities drawn in green in the graph may be used for computation.
A step function $x(t) = γ(t)$ ⇒ $ X_{\rm L} = 1/p$ at the input causes the output signal $y(t)$ to be equal to the step response $σ(t)$ of $H_{\rm L}(p)$ . In addition to the singularities of $H_{\rm L}(p)$, the pole (shown in red in the graph) at $p = 0$ must now also be taken into account for computation.
Only signals for which $X_{ \rm L}(p)$ can be expressed in pole-zero notation are possible as input $x(t)$ (see the table in the chapter "Laplace Transform and $p$–Transfer Function"), for example a cosine or sine signal switched on at time $t = 0$ .
So, a rectangle as input signal $x(t)\ \ ⇒ \ \ X_{\rm L}(p) = (1 - {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot \hspace{0.05cm} T})/p$ is not possible in the approach described here. However, the rectangular response $y(t)$ can be computed indirectly as the difference of two step responses.

Some results of the theory of functions

In contrast to the Fourier integrals, which differ only slightly in the two directions of transformation, for "Laplace" the computation of $y(t)$ from $Y_{\rm L}(p)$ – that is the inverse transformation – is

much more difficult than computing $Y_{\rm L}(p)$ from $y(t)$,
unresolvable or solvable only very laboriously by elementary means.

$\text{Definition:}$ In general, the following holds for the inverse Laplace transformation:

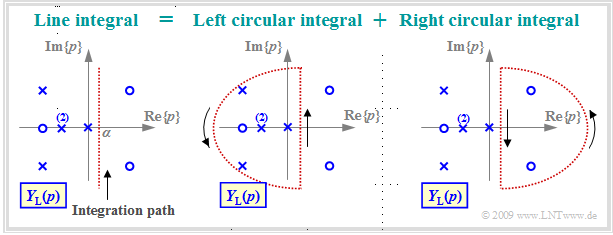
$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}= \lim_{\beta \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} \hspace{0.15cm} \frac{1}{ {\rm j} \cdot 2 \pi}\cdot \int_{ \alpha - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta } ^{\alpha+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta} Y_{\rm L}(p) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm}{\rm d}p \hspace{0.05cm} .$$

The integration is parallel to the imaginary axis.
The real part $α$ is to be chosen such that all poles lie to the left of the integration path.

Line integral together with left and right circular integral

The left graph illustrates this line integral along the red dotted vertical ${\rm Re}\{p\}= α$. This integral is solvable using Jordan's lemma of complex analysis. In this tutorial only a very short and simple summary of the approach is depicted:

The line integral can be divided into two circular integrals according to the sketch so that all poles are located in the left circular integral while the right circular integral may only contain zeros.
According to the theory of functions, the right circular integral yields the time function $y(t)$ for negative times. Due to causality, $y(t < 0)$ must be identical to zero, but according to the fundamental theorem of the theory of functions this is only true if there are no poles in the right $p$–half-plane.
Das Integral über den linken Halbkreis liefert dagegen die Zeitfunktion für $t ≥ 0$. Dieses umschließt alle Polstellen und ist mit dem Residuensatz in (relativ) einfacher Weise berechenbar, wie auf den nächsten Seiten gezeigt wird.

Formulation of the residue theorem

Es wird weiter vorausgesetzt, dass die Übertragungsfunktion $Y_{\rm L}(p)$ in Pol–Nullstellen–Form durch

den konstanten Faktor $K$,
die $Z$ Nullstellen $p_{{\rm o}i}$ $(i = 1$, ... , $Z)$ und
die $N$ Polstellen $p_{{\rm x}i}$ $(i = 1$, ... , $N$)

dargestellt werden kann. Wir setzen zudem $Z < N$ voraus.

Die Anzahl der unterscheidbaren Pole bezeichnen wir mit $I$. Zur Bestimung von $I$ werden mehrfache Pole nur einfach gezählt. So gilt für die Skizze im letzten Abschnitt unter Berücksichtigung des Poles bei $p=0$ aufgrund der doppelten Polstelle: $N = 5$ und $I = 4$.

$\text{Residuensatz:}$ Unter den genannten Voraussetzungen ergibt sich die Laplace–Rücktransformierte von $Y_{\rm L}(p)$ für Zeiten $t ≥ 0$ als die Summe von $I$ Eigenschwingungen der Pole, die man als die Residuen – abgekürzt mit „Res” – bezeichnet:

$$y(t) = \sum_{i=1}^{I}{\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}_i}} \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p \hspace{0.05cm}t}\} \hspace{0.05cm} .$$

Da $Y_{\rm L}(p)$ nur für kausale Signale angebbar ist, gilt für negative Zeiten stets $y(t < 0) = 0$.

Für einen Pol der Vielfachheit $l$ gilt allgemein:

$${\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{1}{(l-1)!}\cdot \frac{ {\rm d}^{\hspace{0.05cm}l-1} }{ {\rm d}p^{\hspace{0.05cm}l-1} }\hspace{0.15cm} \left \{Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i})^{\hspace{0.05cm}l}\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg \vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$

Als Sonderfall ergibt sich daraus mit $l = 1$ für einen einfachen Pol:

$${\rm Res} \bigg\vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i} )\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$

Auf den nächsten Seiten wird der Residuensatz anhand dreier ausführlicher Beispiele verdeutlicht, die mit den drei Konstellationen im $\text{Beispiel 3}$ im Kapitel "Laplace–Transformation" korrespondieren:

Wir betrachten also wieder den Vierpol mit einer Induktivität $L = 25 \ \rm µH$ im Längszweig sowie im Querzweig die Serienschaltung aus einem Ohmschen Widerstand $R = 50 \ \rm Ω$ und einer Kapazität $C$.
Für Letztere betrachten wir wieder drei verschiedene Werte, nämlich $C = 62.5 \ \rm nF$, $C = 8 \ \rm nF$ und $C = 40 \ \rm nF$.
Vorausgesetzt ist stets $x(t) = δ(t) \; ⇒ \; X_{\rm L}(p) = 1$ ⇒ $Y_{\rm L}(p) = H_{\rm L}(p)$ ⇒ $y(t)$ ist gleich der Impulsantwort $h(t)$.

Aperiodically decaying impulse response

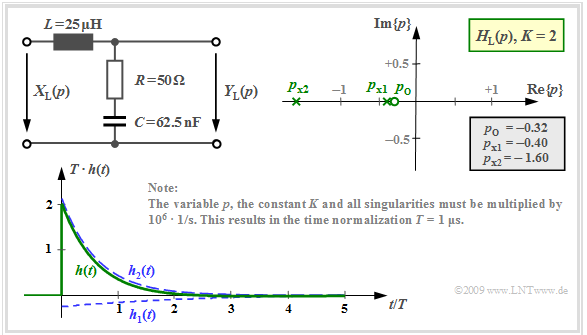
Mit der Kapazität $C = 62.5 \ \rm nF$ und den weiteren in der unteren Grafik angegebenen Zahlenwerten erhält man für die auf der Seite Pol–Nullstellen–Darstellung von Schaltungen berechnete $p$–Übertragungsfunktion:

$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})}= 2 \cdot \frac {p + 0.32 } {(p +0.4)(p +1.6 )} \hspace{0.05cm} .$$

Beachten Sie bitte die Normierung von $p$, $K$ sowie aller Pole und Nullstellen mit dem Faktor ${\rm 10^6} · 1/\rm s$.

Die Impulsantwort setzt sich aus $I = N = 2$ Eigenschwingungen zusammen. Für $t < 0$ sind diese gleich Null.

Das Residium des Pols bei $p_{{\rm x}1} =\ –0.4$ liefert die folgende Zeitfunktion:

$$h_1(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}1})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}=2 \cdot \frac {p + 0.32 } {p +0.4}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.4}= - \frac {2 } {15}\cdot {\rm e}^{-0.4 \hspace{0.05cm} t} \hspace{0.05cm}. $$

In gleicher Weise kann das Residium des zweiten Pols bei $p_{{\rm x}2} = \ –1.6$ berechnet werden:

$$h_2(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}2})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}}=2 \cdot \frac {p + 0.32 } {p +1.6}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1.6}= \frac {32 } {15}\cdot {\rm e}^{-1.6 \hspace{0.05cm} t} \hspace{0.05cm}. $$

Abklingende Impulsantwort

Die Grafik zeigt $h_1(t)$ und $h_2(t)$ sowie das Summensignal $h(t)$.

Berücksichtigt ist auch hier der Normierungsfaktor $1/T = 10^6 · \rm 1/s$, so dass die Zeit auf $T = 1 \ \rm µ s$ normiert ist.
Für $t =0$ ergibt sich $T \cdot h(t=0) = {32 }/ {15} -{2 }/ {15}= 2 \hspace{0.05cm}$.
Für Zeiten $t > 2 \ \rm µ s$ ist die Impulsantwort negativ
(wenn auch nur geringfügig und in der Grafik nur schwer zu erkennen).

Attenuated-oscillatory impulse response

Die Bauelementewerte $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 8 \ \rm nF$ ergeben zwei konjugiert komplexe Pole bei $p_{{\rm x}1} = \ –1 + {\rm j} · 2$ und $p_{{\rm x}2} = \ –1 - {\rm j} · 2$. Die Nullstelle liegt bei $p_{\rm o} = \ –2.5$. Es gilt $K = 2$ und alle Zahlenwerte sind wieder mit dem Faktor $1/T$ zu multiplizieren $(T = 1\ \rm µ s$).

Wendet man den Residuensatz auf diese Konfiguration an, so erhält man:

$$h_1(t) = \text{ ...} = K \cdot \frac {p_{\rm x 1} - p_{\rm o }} {p_{\rm x 1} - p_{\rm x 2}}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot \hspace{0.05cm}t}= 2 \cdot \frac {-1 + {\rm j}\cdot 2 +2.5} {(-1 + {\rm j}\cdot 2) - (-1 - {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}= 2 \cdot \frac {1.5 + {\rm j}\cdot 2} {{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}$$

$$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {1.5 + {\rm j}\cdot 2} {{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}= (1 - {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} ,$$

$$ h_2(t) = \text{ ...} = K \cdot \frac {p_{\rm x 2} - p_{\rm o }} {p_{\rm x 2} - p_{\rm x 1}}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot \hspace{0.05cm}t}= 2 \cdot \frac {-1 - {\rm j}\cdot 2 +2.5} {(-1 - {\rm j}\cdot 2) - (-1 + {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t}=2 \cdot \frac {1.5 - {\rm j}\cdot 2} {-{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t} $$

Gedämpft oszillierende Impulsantwort

$$\Rightarrow \hspace{0.3cm}h_2(t) = (1 + {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} . $$

Mit dem Satz von Euler ergibt sich somit für das Summensignal:

$$h(t) = h_1(t) + h_2(t)$$

$$\Rightarrow \hspace{0.3cm}h(t) = {\rm e}^{-t}\cdot \big [ (1 - {\rm j}\cdot 0.75)\cdot (\cos() + {\rm j}\cdot \sin())+ $$

$$\hspace{3.1cm}+ (1 + {\rm j}\cdot 0.75)\cdot (\cos() - {\rm j}\cdot \sin())\big ]$$

$$\Rightarrow \hspace{0.3cm}h(t) ={\rm e}^{-t}\cdot \big [ 2\cdot \cos(2t) + 1.5 \cdot \sin(2t)\big ]\hspace{0.05cm} . $$

Die Grafik zeigt die nun mit ${\rm e}^{–t}$ gedämpft oszillierende Impulsantwort $h(t)$ für diese Pol–Nullstellen–Konfiguration.

Critically-damped case

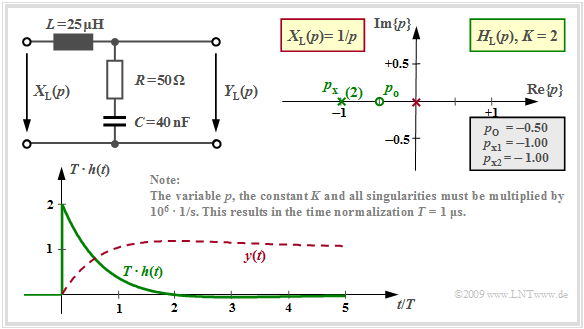
Mit $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 40 \ \rm nF$ ergibt sich der so genannte aperiodische Grenzfall:

$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x })^2}= 2 \cdot \frac {p + 0.5 } {(p +1)^2} \hspace{0.05cm} .$$

Der Kapazitätswert $C = 40 \ \rm nF$ ist der kleinstmögliche Wert, für den sich gerade noch reelle Polstellen ergeben. Diese fallen zusammen, das heißt $p_{\rm x} = \ –1$ ist eine doppelte Polstelle. Die Zeitfunktion lautet somit entsprechend dem Residuensatz mit $l = 2$:

$$h(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm} \left \{H_{\rm L}(p)\cdot (p - p_{ {\rm x} })^2\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } = K \cdot \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm}\left \{ (p - p_{ {\rm o} })\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{0.05cm} .$$

Mit der Produktregel der Differentialrechnung ergibt sich daraus:

Impulsantwort und Sprungantwort des aperiodischen Grenzfalls

$$h(t) = K \cdot \left [ {\rm e}^{p \hspace{0.05cm}t} + (p - p_{ {\rm o} })\cdot t \cdot {\rm e}^{p \hspace{0.05cm}t} \right ] \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1} = {\rm e}^{-t}\cdot \left ( 2 - t \right) \hspace{0.05cm} .$$

Die Grafik zeigt diese Impulsantwort (grüne Kurve) in normierter Darstellung. Sie unterscheidet sich von derjenigen mit den beiden unterschiedlichen Polen bei $-0.4$ und $-1.6$ nur geringfügig.

Das rot gezeichnete Signal $y(t) = 1 - {\rm e}^{-t} + t \cdot {\rm e}^{-t}$ ergibt sich, wenn man am Eingang zusätzlich eine Sprungfunktion berücksichtigt ⇒ Sprungantwort.

Zur Berechnung der Sprungantwort $\sigma(t) = y(t)$ kann man alternativ

bei der Residuenberechnung einen zusätzlichen Pol bei $p = 0$ (rot markiert) berücksichtigen,
oder das Integral über die Impulsantwort $h(t)$ bilden.

Partial fraction decomposition

Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt ⇒ $Z$ muss stets kleiner als $N$ sein.

Gilt dagegen wie bei einem Hochpass $Z = N$, so

ist der Grenzwert der Spektralfunktion für großes $p$ ungleich Null,
beinhaltet das zugehörige Zeitsignal $y(t)$ auch einen Diracimpuls,
versagt der Residuensatz und es ist eine Partialbruchzerlegung vorzunehmen.

Die Vorgehensweise soll beispielhaft für einen Hochpass erster Ordnung verdeutlicht werden.

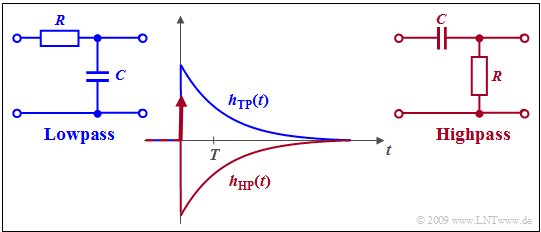
Impulsantwort von Tiefpass (blau) und Hochpass (rot)

$\text{Example 1:}$ Die $p$–Übertragungsfunktion eines $RC$–Hochpasses erster Ordnung kann durch Abspaltung einer Konstanten wie folgt umgewandelt werden:

$$\frac{p}{p + RC} = 1- \frac{RC}{p + RC}\hspace{0.05cm} .$$

Damit lautet die Hochpass–Impulsantwort:

$$h_{\rm HP}(t) = \delta(t) - h_{\rm TP}(t) \hspace{0.05cm} .$$

Die Grafik zeigt

als rote Kurve die Hochpass–Impulsantwort $h_{\rm HP}(t)$,
als blaue Kurve die Impulsantwort $h_{\rm TP}(t)$ des äquivalenten Tiefpasses.

Die Diracfunktion ist die Laplace–Transformierte des konstanten Wertes $1$, während die zweite Funktion die Impulsantwort des äquivalenten Tiefpasses angibt, die mit $Z = 0$, $N =1$ und $K = RC$ durch den Residuensatz angebbar ist.