Some Preliminary Remarks on Two-Dimensional Random Variables

1 # OVERVIEW OF THE THIRD MAIN CHAPTER #
2 Introductory example on the statistical dependence of random variables
3 Prerequisites and nomenclature
4 Probability mass function and probability density function
5 Probability mass function and entropy
6 Informational divergence - Kullback-Leibler distance
7 Joint probability and joint entropy
8 Exercises for the chapter
9 List of sources

# OVERVIEW OF THE THIRD MAIN CHAPTER #

The focus of this third main chapter is the mutual information $I(X; Y)$ between two random variables $X$ and $Y$. With statistical dependence, $I(X; Y)$ is smaller than the individual entropies $H(X)$ or $H(Y)$.

For example, the uncertainty regarding the random variable $X$ ⇒ entropy $H(X)$ is reduced by the knowledge of $Y$, by the amount $H(X\hspace{0.03cm}|\hspace{0.03cm}Y)$ ⇒ conditional entropy of $X$, if $Y$ is known. The remaining residue is the mutual information

$$I(X; Y)= H(X) - H(X\hspace{0.03cm}|\hspace{0.03cm}Y).$$

At the same time, however:

$$I(X; Y) = H(Y) - H(Y\hspace{0.03cm}|\hspace{0.03cm}X).$$

The semicolon indicates that the two random variables $X$ and $Y$ under consideration are on an equal footing.

In detail, the third main chapter deals with

the relationship between probability and entropy for »2D random variables«,
the calculation of the »informational divergence«, also known as the »Kullback–Leibler distance«,
the definition of the »joint entropy« $H(XY)$ and the »conditional entropies« $H(X\hspace{0.03cm}|\hspace{0.03cm}Y)$ and $H(Y\hspace{0.03cm}|\hspace{0.03cm}X)$,
the »mutual information« $I(X; Y)$ between two random variables,
the »information theory of digital signal transmission« and the corresponding model,
the definition and meaning of the »channel capacity« and its connection with the mutual information,
the capacity calculation for »digital memoryless channels« such as BSC, BEC and BSEC,
the »Channel Coding Theorem«, one of the highlights of Shannon's information theory.

Introductory example on the statistical dependence of random variables

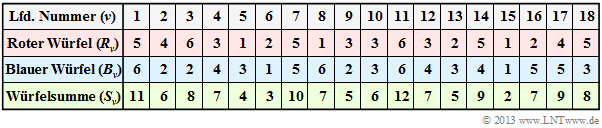
Result protocol of our random experiment "Rolling with two dice"

$\text{Example 1:}$ We start from the experiment "Rolling with two dice", where both dice are distinguishable by colour. The table shows the results of the first $N = 18$ pairs of throws of this exemplary random experiment.
According to the nomenclature explained in the following section $R_ν$, $B_ν$ and $S_ν$ are here to be understood as random variables:

For example, the random variable $R_3 \in \{1, \ 2, \ 3, \ 4, \ 5, \ 6\}$ indicates the number of points of the red cube on the third throw as a probability event. The specification $R_3 = 6$ states that in the documented realisation the red cube showed a "6" in the third throw.

In line 2, the results of the red cube $(R)$ are indicated. The mean value of this limited sequence $〈R_1$, ... , $R_{18}〉$ is with $3.39$ smaller than the expected value ${\rm E}\big[R\big] = 3.5$.
Line 3 shows the results of the blue cube $(B)$. The sequence $〈B_1$, ... , $B_{18}〉$ has a slightly larger mean value of $3.61$ than the unlimited sequence ⇒ expected value ${\rm E}\big[B\big] = 3.5$.
Line 4 contains the sum $S_ν = R_ν + B_ν$. The mean value of the sequence $〈S_1$, ... , $S_{18}〉$ is $3.39 + 3.61 = 7$. This is here (only by chance) equal to the expected value $\text{E}\big[S\big] = \text{E}\big[R\big] + \text{E}\big[B\big]$.

Now the question arises between which random variables there are statistical dependencies:

If one assumes fair dice, there are no statistical dependencies between the sequences $〈 R\hspace{0.05cm} 〉$ and $〈B \hspace{0.05cm}〉$ – whether bounded or unbounded: Even if one knows $R_ν$ for $B_ν$ all possible results $(1$, ... , $6)$ are equally probable.
If one knows $S_ν$, however, statements about $R_ν$ as well as about $B_ν$ are possible. From $S_{11} = 12$ follows directly $R_{11} = B_{11} = 6$ and the sum $S_{15} = 2$ of two dice is only possible with $R_{15} = B_{15} = 1$. Such dependencies are called »deterministic«.
From $S_7 = 10$, at least ranges for $R_7$ and $B_7$ can be given: $R_7 ≥ 4, \ B_7 ≥ 4$. Only three pairs are possible: $(R_7 = 4) ∩ (B_7 = 6)$, $(R_7 = 5) ∩ (B_7 = 5)$, $(R_7 = 6) ∩ (B_7 = 4)$. Here there is no deterministic relationship between the variables $S_ν$ and $R_ν$ $($or $B_ν)$, but rather a so-called »statistical dependence«.
Such statistical dependencies exist for $S_ν ∈ \{3, \ 4, \ 5, \ 6, \ 8, \ 9, \ 10, \ 11\}$. On the other hand, if the sum $S_ν = 7$, one cannot infer $R_ν$ and $B_ν$ from this. For both dice, all possible numbers $1$, ... , $6$ are equally probable. In this case, there are also no statistical dependencies between $S_ν$ and $R_ν$ or between $S_ν$ and $B_ν$.

Prerequisites and nomenclature

Throughout this chapter, we consider discrete-value random variables of the form $X = \{ x_1, \ x_2, \hspace{0.05cm}$ ... $\hspace{0.05cm},\ x_{\mu},\hspace{0.05cm}$ ... $\hspace{0.05cm},\ x_M \} \hspace{0.05cm},$ and use the following nomenclature:

The random variable itself is always denoted by a capital letter. The lower case letter $x$ indicates a possible realisation of the random variable $X$.
All realisations $x_μ$ $($with $μ = 1$, ... , $M)$ are real-valued. $M$ indicates the "symbol set size" or "alphabet size" of $X$. Instead of $M$, we sometimes also use $|X|$.

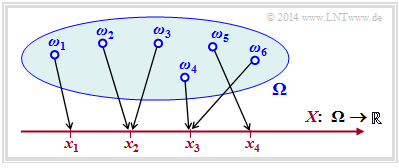
Relationship between the probability space ${\it \Omega}$
and the random variable $X$

The random variable $X$ can, for example, be created by the transformation ${\it \Omega} → X$ , where ${\it \Omega}$ stands for the probability space of a random experiment.

The diagram illustrates such a transformation:

$${\it \Omega} = \{ \omega_1, \omega_2, \omega_3, ... \hspace{0.15cm} \} \hspace{0.25cm} \longmapsto \hspace{0.25cm} X = \{ x_1, \ x_2, \ x_3, \ x_4\} \subset \cal{R}\hspace{0.05cm}.$$

Each random event $ω_i ∈ Ω$ is uniquely assigned to a real numerical value $x_μ ∈ X ⊂ \cal{R}$.
In the example considered, the running variable is $1 ≤ μ ≤ 4$, i.e. the symbol set size is $M = |X| = 4$.
However, the figure is not one-to-one: The realisation $x_3 ∈ X$ could have resulted from the elementary event $ω_4$ in the example, but also from $ω_6$ $($or from some other of the infinitely many elementary events $ω_i$ not drawn in the diagram).

$\text{Agreement:}$ Often one refrains from indexing both the elementary events $ω_i$ and the realisations $x_μ$. This results in the following shorthand notations, for example:

$$ \{ X = x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) = x \} \hspace{0.05cm},$$

$$ \{ X \le x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) \le x \} \hspace{0.05cm}.$$

With this agreement, the probabilities of the discrete random variable $X$ are:

$${\rm Pr}( X = x_{\mu}) = \hspace{-0.2cm} \sum_{\omega \hspace{0.1cm} \in \{ X = x_{\mu} \} } \hspace{-0.2cm}{\rm Pr} \left ( \{ \omega \} \right ) \hspace{0.05cm}.$$

Probability mass function and probability density function

$\text{Definition:}$ If the $M$ probabilities of a discrete random variable $X$ ⇒ ${\rm Pr}( X = x_{\mu})$ are combined in a similar way to a vector,
we arrive at the probability mass function $\rm (PMF)$:

$$P_X(X) = \big [ \hspace{0.02cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...} \hspace{0.15cm}, P_X(x_{\mu}),\hspace{0.05cm} \text{...}\hspace{0.15cm}, P_X(x_M) \hspace{0.02cm} \big ] \hspace{0.05cm}.$$

The $μ$–th element of this "vector" indicates the probability $P_X(x_{\mu}) = {\rm Pr}( X = x_{\mu}) $.

In the book "Theory of Stochastic Signals", we defined a similar descriptive quantity with the probability density function $(\rm PDF)$ and designated it as $f_X(x)$.

It should be noted, however:

The PDF is more suitable for characterising continuous random variables, such as a Gaussian distribution or a uniform distribution. Only through the use of Dirac delta functions does the PDF also become applicable for discrete random variables.
The PMF provides less information about the random variable than the PDF and can also only be specified for discrete variables. However, for the value-discrete information theory considered in this chapter, the PMF is sufficient.

$\text{Example 2:}$ We consider a probability density function $\rm (PDF)$ without much practical relevance:

$$f_X(x) = 0.2 \cdot \delta(x+2) + 0.3 \cdot \delta(x - 1.5)+0.5 \cdot \delta(x - {\rm \pi}) \hspace{0.05cm}. $$

Thus, for the discrete random variable $x ∈ X = \{–2,\ +1.5,\ +\pi \} $ ⇒ symbol set size $M = \vert X \vert = 3$, the probability function $\rm (PMF)$ is:

$$P_X(X) = \big [ \hspace{0.1cm}0.2\hspace{0.05cm}, 0.3\hspace{0.05cm}, 0.5 \hspace{0.1cm} \big] \hspace{0.05cm}. $$

It can be seen:

The $\rm PMF$ only provides information about the probabilities $\text{Pr}(x_1)$, $\text{Pr}(x_2)$ and $\text{Pr}(x_3)$.
From the $\rm PDF$, on the other hand, the possible realisations $x_1$, $x_2$ and $x_3$ of the random variable $X$ can also be read.
The only requirement for the random variable is that it is real-valued.
The possible values $x_μ$ do not have to be positive, integer, equidistant or rational.

Probability mass function and entropy

In value-discrete information theory in contrast to transmission problems, knowledge of the probability mass function $P_X(X)$ is sufficient, e.g. to calculate the entropy.

$\text{Definition:}$ The $\rm entropy$ of a discrete random variable $X$ – i.e. its uncertainty for an observer - can be represented with the PMF $P_X(X)$ as follows:

$$H(X) = {\rm E} \big [ {\rm log} \hspace{0.1cm} \frac{1}{P_X(X)}\big ] \hspace{0.05cm}=\hspace{0.05cm} - {\rm E} \big [ {\rm log} \hspace{0.1cm} {P_X(X)}\big ] \hspace{0.05cm}=\hspace{0.05cm} \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}=\hspace{0.05cm} - \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} {P_X(x_{\mu})} \hspace{0.05cm}.$$

If you use the logarithm to base $2$, i.e. $\log_2$ (...) ⇒ "binary logarithm", the numerical value is provided with the pseudo-unit "bit". $\rm E\big[$...$\big]$ indicates the expected value.

For example, one obtains

with $P_X(X) = \big [\hspace{0.02cm}0.2, \ 0.3, \ 0.5 \hspace{0.02cm}\big ]$:

$$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} +0.5 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5} \approx 1.485\hspace{0.15cm}{\rm bit},$$

with $P_X(X) = \big [\hspace{0.02cm}1/3, \ 1/3, \ 1/3\hspace{0.02cm}\big ]$:

$$H(X) = 3 \cdot 1/3 \cdot {\rm log}_2 \hspace{0.1cm} (3) = {\rm log}_2 \hspace{0.1cm} (3) \approx 1.585\hspace{0.15cm}{\rm bit}.$$

The second example provides the maximum of the entropy function for the symbol set size $M = 3$.

$\text{Derivation:}$ For general $M$, this result can be derived e.g. as follows – see [Meck]^[1]:

$$H(X) = -{\rm E} \big [ {\rm log} \hspace{0.1cm} {P_X(X)}\big ] \hspace{0.2cm} \le \hspace{0.2cm}- {\rm log} \big [ {\rm E} \hspace{0.1cm} \left [{P_X(X)}\right ] \big ] \hspace{0.05cm}.$$

This estimation $($Jensens's inequality$)$ is admissible because the logarithm is a concave function. According to Exercise 3.2 , the following holds:

$$- {\rm E} \big [ {P_X(X)}\big ] \hspace{0.1cm} \le \hspace{0.1cm} M \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H(X) \le {\rm log} \hspace{0.1cm} (M) \hspace{0.05cm}.$$

The equal sign results according to the calculation above for equal probabilities, i.e. for $P_X(x_μ) = {1}/{M}$ for all $μ$. In Exercise 3.3, the same situation is to be proved using the estimate "${\rm ln} \hspace{0.1cm} (x) \le x-1$". The equal sign applies here only for $x = 1$.

If one of the $M$ probabilities $P_X(x_μ)$ of the PMF is equal to zero, a tighter bound can be given for the entropy:

$$H(X) \le {\rm log} \hspace{0.1cm} (M-1) \hspace{0.05cm}.$$

$\text{Agreement:}$ In the following example and on the next pages we use the following nomenclature:

The entropy $H(X)$ always refers to the actual probability mass function $P_X(X)$ of the discrete random variable. Experimentally, these quantities are obtained only after $N → ∞$ trials.
If the PMF is determined from a finite random sequence, we denote this probability mass function by $Q_X(X)$ and add „$N =$ ...” to the resulting entropy.
This entropy approximation is not based on probabilities, but only on the relative frequencies. Only for $N → ∞$ does this approximation agree with $H(X)$ .

Probability mass functions of our dice experiment

$\text{Example 3:}$ We return to our "dice experiment".

The table shows the probability mass functions $P_R(R)$ and $P_B(B)$ for the red and blue dice as well as the approximations $Q_R(R)$ and $Q_B(B)$, in each case based on the random experiment with $N = 18$ throws.
The relative frequencies $Q_R(R)$ and $Q_B(B)$ result from the exemplary random sequences of $\text{Example 1}$.

The following applies to the random variable $R$ with the "binary logarithm" $($to base $2)$:

$$H(R) = H(R) \big \vert_{N \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} = \sum_{\mu = 1}^{6} 1/6 \cdot {\rm log}_2 \hspace{0.1cm} (6) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\hspace{0.1cm} {\rm bit} ,$$

$$H(R) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 2 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm} +\hspace{0.1cm} 2 \cdot \frac{3}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{3} \hspace{0.1cm} +\hspace{0.1cm} 2 \cdot \frac{4}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{4} \hspace{0.1cm}= 2.530\hspace{0.1cm} {\rm bit}.$$

The blue cube of course has the same entropy: $H(B) = H(R) = 2.585\ \rm bit$. Here we get a slightly larger value for the approximation based on $N = 18$ , since according to the table above $Q_B(B)$ deviates less from the discrete uniform distribution $P_B(B)$ than als $Q_R(R)$ from $P_R(R)$.

$$H(B) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 1 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm} +\hspace{0.1cm} 4 \cdot \frac{3}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{3} \hspace{0.1cm} +\hspace{0.1cm} 1 \cdot \frac{4}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{4} \hspace{0.1cm}= 2.558\hspace{0.1cm} {\rm bit} .$$

It can be seen from the given numerical values that despite the experimental parameter $N$, which is here much too small, the deviation with regard to entropy is not very large.

It should be mentioned again that with finite $N$ the following always applies:

$$ H(R) \big \vert_{N } < H(R) = {\rm log}_2 \hspace{0.1cm} (6) \hspace{0.05cm}, \hspace{0.5cm} H(B) \big \vert_{N } < H(B) = {\rm log}_2 \hspace{0.1cm} (6)\hspace{0.05cm}.$$

Informational divergence - Kullback-Leibler distance

We consider two probability mass functions $P_X(·)$ and $P_Y(·)$ over the same alphabet $X = \{ x_1, \ x_2$, ... , $x_M \}$, and now define the following quantity:

$\text{Definition:}$ The informational divergence between the random variables defined by $P_X(·)$ and $P_Y(·)$ is given as follows:

$$D(P_X \hspace{0.05cm} \vert \vert \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x_{\mu})}{P_Y(x_{\mu})} \hspace{0.05cm}.$$

$D(P_X \vert \vert P_Y)$ is also called Kullback–Leibler distance .

This provides a measure of the "similarity" between the two probability functions $P_X(·)$ and $P_Y(·)$.

When using the logarithm to base $2$ the pseudo-unit "bit" must be added again.

Similarly, a second variant of the Kullback-Leibler distance can be given:

$$D(P_Y \hspace{0.05cm} || \hspace{0.05cm}P_X) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M} P_Y(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_Y(x_{\mu})}{P_X(x_{\mu})} \hspace{0.05cm}.$$

Compared to the first variant, each function $P_X(·)$ is now replaced by $P_Y(·)$ and vice versa. Since in general $D(P_X || P_Y)$ and $D(P_Y || P_X)$ differ, the term "distance" is actually misleading. However, we want to leave it at this naming.

If we evaluate the two equations above, we recognise the following properties:

If the same distribution is present ⇒ $P_Y(·) ≡ P_X(·)$, then $D(P_X || P_Y) = 0$. In all other cases $D(P_X || P_Y) > 0$. The same applies to the variant $D(P_Y || P_X)$.
If $P_X(x_μ) ≠ 0$ and $P_Y(x_μ) = 0$ $($a single and arbitrary $μ$ is sufficient for this$)$, the Kullback-Leibler distance $D(P_X || P_Y)$ has an infinitely large value. In this case,
$D(P_Y || P_X)$ is not necessarily infinite either.
This statement makes it clear once again that in general $D(P_X || P_Y)$ will be unequal to $D(P_Y || P_X)$ .

Subsequently, these two definitions are clarified with our standard example "dice experiment". At the same time we refer to the following exercises:

Probability mass functions of our dice experiment

$\text{Example 4:}$ For the dice experiment, we defined in $\text{Example 3}$ the probability mass functions $P_R(·)$ and $P_B(·)$ and their approximations $Q_R(·)$ and $Q_B(·)$ .

The random variable $R$ with the probability mass function $P_R(·)$ indicates the numbers of the red cube and $B$ the numbers of the blue cube ⇒ PMF $P_B(·)$.
The approximations $Q_R(·)$ and $Q_B(·)$ result from the former experiment with $N = 18$ double throws ⇒ $\text{Example 1}$ .

Then holds:

Since $P_R(·)$ and $P_B(·)$ are identical, we obtain zero for each of the Kullback-Leibler distances $D(P_R \vert \vert P_B)$ and $D(P_B \vert \vert P_R)$.
The comparison of $P_R(·)$ and $Q_R(·)$ yields for the first variant of the Kullback-Leibler distance:

$$\begin{align*}D(P_R \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_R) & = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_R(\cdot)}{Q_R(\cdot)}\right ] \hspace{0.1cm} = \sum_{\mu = 1}^{6} P_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_R(r_{\mu})}{Q_R(r_{\mu})} = \\ & = {1}/{6} \cdot \left [ 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{2/18} \hspace{0.1cm} + 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{3/18} \hspace{0.1cm} + 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{4/18} \hspace{0.1cm} \right ] = 1/6 \cdot \big [ 2 \cdot 0.585 + 2 \cdot 0 - 2 \cdot 0.415 \big ] \approx 0.0570\hspace{0.15cm} {\rm bit} .\end{align*}$$

In the calculation of the expected value, the fact that $P_R(r_1) = $ ... $ = P_R(r_6)$, the factor 1/6 can be excluded. Since the logarithm to base $ 2$ was used here, the pseudo-unit "bit” is added.

For the second variant of the Kullback-Leibler distance, a slightly different value results:

$$\begin{align*}D(Q_R \hspace{0.05cm}\vert \vert \hspace{0.05cm} P_R) & = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{Q_R(\cdot)}{P_R(\cdot)}\right ] \hspace{0.1cm} = \sum_{\mu = 1}^{6} Q_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{Q_R(r_{\mu})}{P_R(r_{\mu})} \hspace{0.05cm} = \\ & = 2 \cdot \frac{2}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2/18}{1/6} \hspace{0.1cm} + 2 \cdot \frac{3}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{3/18}{1/6} \hspace{0.1cm} + 2 \cdot \frac{4}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4/18}{1/6} \approx 0.0544\hspace{0.15cm} {\rm bit} .\end{align*}$$

For the blue cube, one obtains $D(P_B \vert \vert Q_B) ≈ 0.0283 \hspace{0.15cm} \rm bit$ and $D(Q_B \vert \vert P_B) ≈ 0.0271 \hspace{0.15cm} \rm bit$, i.e. slightly smaller Kullback-Leibler distances, since the approximation $Q_B(·)$ of $P_B(·)$ differs less than $Q_R(·)$ of $P_R(·)$.
Comparing the frequencies $Q_R(·)$ and $Q_B(·)$, we get $D(Q_R \vert \vert Q_B) ≈ 0.0597 \hspace{0.15cm} \rm bit$ and $D(Q_B \vert \vert Q_R) ≈ 0.0608 \hspace{0.15cm} \rm bit$. Here the distances are greatest, since the differences between $Q_B(·)$ and $Q_R(·)$ are greater than between $Q_R(·)$ and $P_R(·)$ or between $Q_B(·)$ and $P_B(·)$.

Joint probability and joint entropy

For the remainder of this third chapter, we always consider two discrete random variable $X = \{ x_1, \ x_2$, ... , $x_M \}$ and $Y = \{ y_1, \ y_2$, ... , $y_K \}$, whose value ranges do not necessarily have to coincide. This means: $K ≠ M$ $($in other notation: $|Y| ≠ |X|)$ is quite permissible.

The probability mass function thus has a $K×M$ matrix form with the elements

$$P_{XY}(X = x_{\mu}\hspace{0.05cm}, \ Y = y_{\kappa}) = {\rm Pr} \big [( X = x_{\mu})\hspace{0.05cm}\cap \hspace{0.05cm} (Y = y_{\kappa}) \big ] \hspace{0.05cm}.$$

We use $P_{XY}(X, Y)$ as a shorthand notation. The new random variable $XY$ contains both the properties of $X$ and those of $Y$.

$\text{Definition:}$ The joint entropy can be represented with the two-dimensional probability mass function $P_{XY}(X, Y)$ as an expected value as follows:

$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] = \sum_{\mu = 1}^{M} \hspace{0.1cm} \sum_{\kappa = 1}^{K} \hspace{0.1cm} P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa})} \hspace{0.05cm}.$$

In the following we use throughout the logarithm to the base $2$ ⇒ $\log(x) → \log_2(x)$. The numerical value is thus to be assigned the pseudo-unit "bit".

In general, the following upper bound can be given for the joint entropy:

$$H(XY) \le H(X) + H(Y) \hspace{0.05cm}.$$

This inequality expresses the following fact:

The equal sign only applies to the special case of statistically independent random variables, as demonstrated in the following $\text{Example 5}$ using the random variables $R$ and $B$ . Here $R$ and $B$ denote the numbers of the red and blue dice, respectively:

$$H(RB) = H(R) + H(B).$$

If, on the other hand, there are statistical dependencies as in $\text{example 6}$ between the random variables $R$ and $S = R + B$, the „<” sign applies in the above inequality:

$$H(RS) < H(R) + H(S).$$

These examples also show to what extent the joint entropies $H(RB)$ and $H(RS)$ change if one does not determine an infinite number of pairs of throws in the dice experiment, but only $N = 18$.

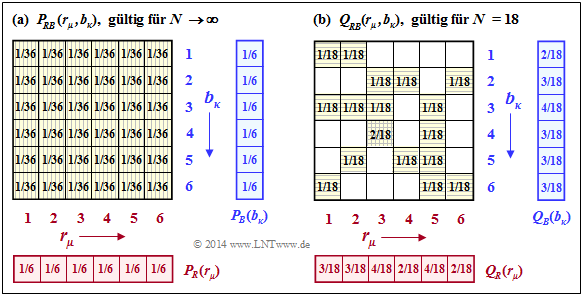
Two-dimensional probability mass function $P_{RB}$ and approximation $Q_{RB}$

$\text{Example 5:}$ We return to the experiment Rolling with two dice :

The random variables are the points of the

red cube: ⇒ $R = \{1, \ 2,\ 3,\ 4,\ 5,\ 6\}$,
blue cube: ⇒ $B = \{1,\ 2,\ 3,\ 4,\ 5,\ 6\}$.

The left graph shows the probabilities

$$P_{RB}(r_\mu,\ b_\kappa ) ={\rm Pr}\big [(R=r_\mu) \hspace{0.05cm}\cap \hspace{0.05cm} (B=b_\kappa)\big],$$

which for all $μ = 1$, ... , $6$ and for all $κ = 1$, ... , $6$ equally yield the value $1/36$. Thus, one obtains for the joint entropy:

$$H(RB) = H(RB) \big \vert_{N \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} = {\rm log}_2 \hspace{0.1cm} (36) = 5.170\hspace{0.05cm} {\rm bit} .$$

One can see from the left graph and the equation given here:

Since $R$ and $B$ are statistically independent of each other, the following applies.

$$P_{RB}(R, B) = P_R(R) · P_B(B).$$

The joint entropy is the sum of the two individual entropies:

$$H(RB) = H(R) + H(B).$$

The right graph shows the approximated two-dimensional probability mass function $Q_{RB}(·)$, based on the only $N = 18$ throws of our experiment. Here, no quadratic form of the joint probability $Q_{RB}(·)$ results, and the joint entropy derived from it is significantly smaller than $H(RB)$:

$$H(RB) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 16 \cdot \frac{1}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{1} \hspace{0.1cm} +\hspace{0.1cm} 1 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm}= 4.059\hspace{0.15cm} {\rm bit} .$$

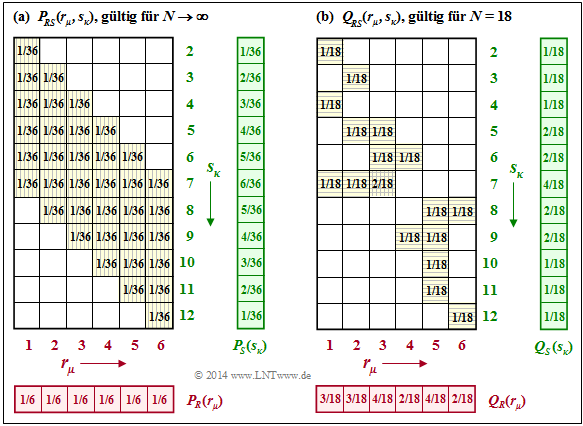
Two-dimensional probability mass function $P_{RS}$ and approximation $Q_{RS}$

$\text{Example 6:}$ In the dice experiment, in addition to the random variables $R$ (red cube) and $B$ (blue cube) also the sum $S = R + B$ is considered. The graph on the left shows that the two-dimensional probability mass function $P_{RS}(·)$ cannot be written as a product of $P_R(·)$ and $P_S(·)$.

With the probability functions

$$P_R(R) = 1/6 \cdot \big [ 1,\ 1,\ 1,\ 1,\ 1,\ 1 \big ],$$

$$P_S(S)=1/36 \cdot \big [ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 5,\ 4,\ 3,\ 2,\ 1 \big ] $$

one obtains for the entropies:

$$H(RS) = {\rm log}_2 \hspace{0.1cm} (36) \approx 5.170\hspace{0.15cm} {\rm bit} ,$$

$$H(R) = {\rm log}_2 \hspace{0.1cm} (6) \approx 2.585\hspace{0.15cm} {\rm bit},$$

$$H(S) = 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\frac{1}{36} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{36}{1} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{2}{36} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{36}{2} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{3}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{3} \hspace{0.05cm} + $$

$$+ 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{4}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{4} \hspace{0.05cm} +2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{5}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{5} + 1 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{6}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{6} $$

$$\Rightarrow \hspace{0.3cm} H(S) \approx 3.274\hspace{0.15cm} {\rm bit} . $$

From these numerical values one can see:

The comparison with the $\text{Example 5}$ shows that $H(RS) =H(RB)$. The reason for this is that, knowing $R$ the random variables $B$ and $S$ give exactly the same information.

Due to the statistical dependence between the red cube and the sum, $H(RS) ≈ 5.170 \hspace{0.15cm} \rm bit$ is smaller than the sum $H(R) + H(S) ≈ 5.877 \hspace{0.15cm} \rm bit.$

Shown on the right is the case where the two-dimensional probability mass function $Q_{RS}(·)$ was determined empirically $(N = 18)$. Although a completely different figure emerges due to the very small $N$ value, the approximation for $H(RS)$ provides exactly the same value as the approximation for $H(RB)$ in $\text{Example 5}$:

$$H(RS) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = H(RB) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 4.059\,{\rm bit} \hspace{0.05cm}.$$