Difference between revisions of "Digital Signal Transmission/Signals, Basis Functions and Vector Spaces"
| (63 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Generalized Description of Digital Modulation Methods |
|Vorherige Seite=Viterbi–Empfänger | |Vorherige Seite=Viterbi–Empfänger | ||
|Nächste Seite=Struktur des optimalen Empfängers | |Nächste Seite=Struktur des optimalen Empfängers | ||
}} | }} | ||
| − | == # | + | == # OVERVIEW OF THE FOURTH MAIN CHAPTER # == |
| − | + | <br> | |
| − | + | The fourth main chapter provides an abstract description of digital signal transmission, which is based on basis functions and signal space constellations. This makes it possible to treat very different configurations – for example band-pass systems and those for the baseband – in a uniform way. The optimal receiver in each case has the same structure in all cases. | |
| − | + | The following are dealt with in detail: | |
| − | + | # The meaning of »basis functions« and finding them using the »Gram-Schmidt process«, | |
| − | + | # the »structure of the optimal receiver« for baseband transmission, | |
| − | + | # the »theorem of irrelevance« and its importance for the derivation of optimal detectors, | |
| − | + | # the »optimal receiver for the AWGN channel« and implementation aspects, | |
| − | + | # the system description by »complex or $N$–dimensional Gaussian noise«, | |
| − | + | # the »error probability calculation and approximation« under otherwise ideal conditions, | |
| − | + | # the application of the signal space description to »carrier frequency systems«, | |
| − | + | # the different results for »OOK, M-ASK, M-PSK, M-QAM and M-FSK«, | |
| − | + | # the different results for »coherent and non-coherent demodulation«. | |
| − | + | Almost all results of this chapter have already been derived in previous sections. However, the approach is fundamentally new: | |
| − | * | + | *In the $\rm LNTwww$ book "Modulation Methods" and in the first three chapters of this book, the specific system properties were already taken into account in the derivations – for example, whether the digital signal is transmitted in baseband or whether digital amplitude, frequency or phase modulation is present.<br> |
| − | |||
| − | + | *Here the systems are to be abstracted in such a way that they can be treated uniformly. The optimal receiver in each case has the same structure in all cases, and the error probability can also be specified for non-Gaussian distributed noise.<br><br> | |
| − | * | ||
| − | |||
| − | |||
| − | + | It should be noted that this rather global approach means that certain system deficiencies can only be recorded very imprecisely, such as | |
| + | *the influence of a non-optimal receiver filter on the error probability,<br> | ||
| + | *an incorrect threshold $($threshold drift$)$, or<br> | ||
| + | *phase jitter $($fluctuations in sampling times$)$.<br><br> | ||
| − | + | In particular in the presence of intersymbol interference, the procedure should therefore continue in accordance with the [[Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference#.23_OVERVIEW_OF_THE_THIRD_MAIN_CHAPTER_.23|third main chapter]]. <br> | |
| − | + | The description is based on the script [KöZ08]<ref name='KöZ08'>Kötter, R., Zeitler, G.: Lecture notes, Institute for Communications Engineering, Technical University of Munich, 2008.</ref> by [[Biographies_and_Bibliographies/Chair_holders_of_the_LNT_since_1962#Prof._Dr._Ralf_K.C3.B6tter_.282007-2009.29|Ralf Kötter]] and [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Dr.-Ing._Georg_Zeitler_.28at_LNT_from_2007-2012.29|Georg Zeitler]], which is closely based on the textbook [WJ65]<ref name='WJ65'>Wozencraft, J. M.; Jacobs, I. M.: Principles of Communication Engineering. New York: John Wiley & Sons, 1965.</ref>. [[Biographies_and_Bibliographies/Chair_holders_of_the_LNT_since_1962#Prof._Dr._sc._techn._Gerhard_Kramer_.28seit_2010.29|Gerhard Kramer]], who has held the chair at the LNT since 2010, treats the same topic with very similar nomenclature in his lecture [Kra17]<ref>Kramer, G.: Nachrichtentechnik 2. Lecture notes, Institute for Communications Engineering, Technical University of Munich, 2017.</ref>. In order not to make reading unnecessarily difficult for our own students at TU Munich, we stick to this nomenclature as far as possible, even if it deviates from other $\rm LNTwww$ chapters.<br> | |
| − | == | + | == Nomenclature in the fourth chapter== |
<br> | <br> | ||
| − | + | Compared to the other $\rm LNTwww$ chapters, the following nomenclature changes arise here: | |
| − | * | + | *The [[Signal_Representation/Principles_of_Communication#Message_-_Information_-_Signal|"message"]] to be transmitted is an integer value $m \in \{m_i\}$ with $i = 0$, ... , $M-1$, where $M$ specifies the "symbol set size". <br>If it simplifies the description, $i = 1$, ... , $M$ is induced.<br> |
| − | |||
| − | * | + | *The result of the decision process at the receiver is also an integer with the same symbol alphabet as at the transmitter. <br>This result is also referred to as the "estimated value": |
| − | :$$\hat{m} \in \{m_i \}, \hspace{0.2cm} i = 0, 1, \text{...}\hspace{0.05cm} , M-1\hspace{0.2cm} ({\rm | + | :$$\hat{m} \in \{m_i \}, \hspace{0.2cm} i = 0, 1, \text{...}\hspace{0.05cm} , M-1\hspace{0.2cm} ({\rm or}\,\,i = 1, 2, \text{...}\hspace{0.05cm}, M) \hspace{0.05cm}.$$ |
| − | + | *The [[Digital_Signal_Transmission/Redundancy-Free_Coding#Symbol_and_bit_error_probability|"symbol error probability"]] $\rm Pr(symbol\hspace{0.15cm} error)$ or $p_{\rm S}$ is usually referred to as follows in this main chapter: | |
| − | * | ||
:$${\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) = 1 - {\rm Pr} ({\cal C}), | :$${\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) = 1 - {\rm Pr} ({\cal C}), | ||
| − | \hspace{0.4cm}\text{ | + | \hspace{0.4cm}\text{complementary event:}\hspace{0.2cm} {\rm Pr} ({\cal C}) = {\rm Pr} ( \hat{m} = m) \hspace{0.05cm}.$$ |
| − | * | + | *In a [[Theory_of_Stochastic_Signals/Probability_Density_Function|"probability density function"]] $\rm (PDF)$, a distinction is made between the "random variable" ⇒ $r$ and the "realization" ⇒ $\rho$ according to $p_r(\rho)$. <br>Formerly, $f_r(r)$ was used for this PDF. <br> |
| + | *With the notation $p_r(\rho)$, $r$ and $\rho$ are scalars. On the other hand, if random variable and realization are vectors (of suitable length), this is expressed in bold type: $p_{ \boldsymbol{ r}}(\boldsymbol{\rho})$ with the vectors $ \boldsymbol{ r}$ and $\boldsymbol{\rho}$. | ||
| − | * | + | *In order to avoid confusion with energy values, the "threshold value is" now called $G$ instead of $E$. This is mainly referred to as the "decision threshold" in this chapter. |
| − | + | *Based on the two real and energy-limited time functions $x(t)$ and $y(t)$, the [https://de.wikipedia.org/wiki/Inneres_Produkt "inner product"] is: | |
| − | * | ||
| − | |||
| − | |||
| − | |||
:$$<\hspace{-0.1cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.1cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t | :$$<\hspace{-0.1cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.1cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | * This results in the [https://en.wikipedia.org/wiki/Euclidean_space#Euclidean_norm "Euclidean norm"] or "2–norm" $($or "norm" for short$)$: | |
| − | * | ||
:$$||x(t) || = \sqrt{<\hspace{-0.1cm}x(t), \hspace{0.05cm}x(t) \hspace{-0.1cm}>} | :$$||x(t) || = \sqrt{<\hspace{-0.1cm}x(t), \hspace{0.05cm}x(t) \hspace{-0.1cm}>} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | *Compared to the script [KöZ08]<ref name='KöZ08' />, the naming differs as follows: | ||
| + | #The probability of the event $E$ is ${\rm Pr}(E)$ instead of $P(E)$. <br>This nomenclature change was also made because in some equations "probabilities" and "powers" appear together.<br> | ||
| + | #Band–pass signals are still marked with the index "BP" and not with a tilde as in [KöZ08]<ref name='KöZ08' />. <br>The corresponding "low-pass signal" is (usually) provided with the index "TP" $($from German "Tiefpass"$)$.<br> | ||
| − | + | == Orthonormal basis functions == | |
| − | |||
| − | |||
| − | |||
| − | = | ||
<br> | <br> | ||
| − | + | In this chapter, we assume a set $\{s_i(t)\}$ of possible transmitted signals that are uniquely assigned to the possible messages $m_i$. With $i = 1$, ... , $M$ holds: | |
| − | + | :$$m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: \hspace{0.3cm} m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.$$ | |
| − | : | ||
| − | + | For what follows, we further assume that the $M$ signals $s_i(t)$ are [[Signal_Representation/Signal_classification#Energy.E2.80.93Limited_and_Power.E2.80.93Limited_Signals| "energy-limited"]], which usually means at the same time that they are of finite duration.<br> | |
| − | {{ | + | {{BlaueBox|TEXT= |
| + | $\text{Theorem:}$ Any set $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ of energy-limited signals can be evolved into $N \le M$ '''orthonormal basis functions''' $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$. It holds: | ||
| − | : | + | :$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , |
| − | \hspace{0.3cm}i = 1,\hspace{0.05cm} ...\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} ... \hspace{0.1cm}, N | + | \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N |
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$ |
| − | + | *In each case, two basis functions $\varphi_j(t)$ and $\varphi_k(t)$ must be orthonormal to each other, that is, it must hold <br>$(\delta_{jk}$ is called [https://en.wikipedia.org/wiki/Kronecker_delta "Kronecker symbol"] or "Kronecker delta"$)$: | |
| − | : | + | :$$<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = |
\left\{ \begin{array}{c} 1 \\ | \left\{ \begin{array}{c} 1 \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm | + | \begin{array}{*{1}c} {\rm if}\hspace{0.1cm}j = k |
| − | \\ {\rm | + | \\ {\rm if}\hspace{0.1cm} j \ne k \\ \end{array} |
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$}}<br> |
| − | + | Here, the parameter $N$ indicates how many basis functions $\varphi_j(t)$ are needed to represent the $M$ possible transmitted signals. In other words: $N$ is the "dimension of the vector space" spanned by the $M$ signals. Here, the following holds: | |
| − | + | #If $N = M$, all transmitted signals are orthogonal to each other. | |
| − | + | #They are not necessarily orthonormal, i.e. the energies $E_i = <\hspace{-0.1cm}s_i(t), \hspace{0.05cm}s_i(t) \hspace{-0.1cm}>$ may well be unequal to one.<br> | |
| + | #$N < M$ arises when at least one signal $s_i(t)$ can be represented as linear combination of basis functions $\varphi_j(t)$ that have resulted from other signals $s_j(t) \ne s_i(t)$. <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 1:}$ We consider $M = 3$ energy-limited signals according to the graph. One recognizes immediately: | ||
| + | [[File:P ID1993 Dig T 4 1 S2 version1.png|right|frame|Representation of three transmitted signals by two basis functions|class=fit]] | ||
| − | * | + | *The signals $s_1(t)$ and $s_2(t)$ are orthogonal to each other.<br> |
| − | + | *The energies are $E_1 = A^2 \cdot T = E$ and $E_2 = (A/2)^2 \cdot T = E/4$.<br> | |
| − | |||
| − | * | + | *The basis functions $\varphi_1(t)$ and $\varphi_2(t)$ are equal in form to $s_1(t)$ and $s_2(t)$, resp., and both have energy one: |
| − | : | + | :$$\varphi_1(t)=\frac{s_1(t)}{\sqrt{E_1} } = \frac{s_1(t)}{\sqrt{A^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_1(t)}{A}$$ |
| − | + | :$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},$$ | |
| + | :$$\varphi_2(t) =\frac{s_2(t)}{\sqrt{E_2} } = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}$$ | ||
| + | :$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = {\sqrt{E} }/{2}\hspace{0.05cm}.$$ | ||
| − | :: | + | *$s_3(t)$ can be expressed by the previously determined basis functions $\varphi_1(t)$, $\varphi_2(t)$: |
| + | :$$s_3(t) =s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},$$ | ||
| + | :$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm} | ||
| + | s_{31} = {A}/{2} \cdot \sqrt {T}= {\sqrt{E} }/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.$$ | ||
| − | |||
| − | + | ⇒ In the lower right image, the signals are shown in a two-dimensional representation | |
| + | *with the basis functions $\varphi_1(t)$ and $\varphi_2(t)$ as axes, | ||
| + | *where $E = A^2 \cdot T$ and the relation to the other graphs can be seen by the coloring. | ||
| − | |||
| − | |||
| − | |||
| − | + | ⇒ The vectorial representatives of the signals $s_1(t)$, $s_2(t)$ and $s_3(t)$ in the two-dimensional vector space can be read from this sketch as follows: | |
| + | :$$\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), $$ | ||
| + | :$$\mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), $$ | ||
| + | :$$\mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.$$}} | ||
| + | <br clear= all> | ||
| − | + | == The Gram-Schmidt process== | |
| − | + | <br> | |
| − | + | In $\text{Example 1}$ in the last section, the specification of the two orthonormal basis functions $\varphi_1(t)$ and $\varphi_2(t)$ was very easy, because they were of the same form as $s_1(t)$ and $s_2(t)$, respectively. The [https://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process "Gram-Schmidt process"] finds the basis functions $\varphi_1(t)$, ... , $\varphi_N(t)$ for arbitrary predefinable signals $s_1(t)$, ... , $s_M(t)$, as follows: | |
| − | * | + | *The first basis function $\varphi_1(t)$ is always equal in form to $s_1(t)$. It holds: |
| + | :$$\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm or }}\hspace{0.2cm} j \ge 2 | ||
| + | \hspace{0.05cm}.$$ | ||
| − | : | + | *It is now assumed that from the signals $s_1(t)$, ... , $s_{k-1}(t)$ the basis functions $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ have been calculated $(n \le k)$. Then, using $s_k(t)$, we compute the auxiliary function |
| − | s_{kj} = \hspace{0.1cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.1cm} >, \hspace{0.2cm} j = 1, ... \hspace{0. | + | :$$\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm with}\hspace{0.4cm} |
| + | s_{kj} = \hspace{0.1cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.1cm} >, \hspace{0.2cm} j = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm}, n-1\hspace{0.05cm}.$$ | ||
| − | * | + | *If $\theta_k(t) \equiv 0$ ⇒ $||\theta_k(t)|| = 0$, then $s_k(t)$ does not yield a new basis function. Rather, $s_k(t)$ can then be expressed by the $n-1$ basis functions $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ already found before: |
| + | :$$s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.$$ | ||
| − | :: | + | *A new basis function $($namely, the $n$–th$)$ results if $||\theta_k(t)|| \ne 0$: |
| + | :$$\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.$$ | ||
| − | + | This process is continued until all $M$ signals have been considered. Then all $N \le M$ orthonormal basis functions $\varphi_j(t)$ have been found. The special case $N = M$ arises only if all $M$ signals are linearly independent.<br> | |
| − | :: | + | :*This process is now illustrated by an example. |
| − | + | :*We also refer to the (German language) HTML5/JavaScript applet [https://www.lntwww.de/Applets:Das_Gram-Schmidt-Verfahren "Das Gram-Schmidt-Verfahren"] ⇒ "Gram–Schmidt process". | |
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 2:}$ We consider the $M = 4$ energy-limited signals $s_1(t)$, ... , $s_4(t)$. To simplify the calculations, both amplitude and time are normalized here. | ||
| − | [[ | + | [[File:P ID1990 Dig T 4 1 S3 version1.png|center|frame|Gram-Schmidt process|class=fit]] |
| − | + | One can see from these sketches: | |
| − | + | *The basis function $\varphi_1(t)$ is equal in form to $s_1(t)$. Because $E_1 = \vert \vert s_1(t) \vert \vert ^3 = 3 \cdot 0.5^2 = 0.75$, we get $s_{11} = \vert \vert s_1(t) \vert \vert = 0.866$. $\varphi_1(t)$ itself has section-wise values $\pm 0.5/0.866 = \pm0.577$. | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | *To calculate the auxiliary function $\theta_2(t)$, we compute |
| − | : | + | :$$s_{21} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.05cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0 \cdot (+0.577) + 1 \cdot (-0.577)+ 0 \cdot (-0.577)= -0.577$$ |
| − | : | + | :$$ \Rightarrow \hspace{0.3cm}\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = (0.333, 0.667, -0.333) |
| − | : | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\vert \vert \theta_2(t) \vert \vert^2 = (1/3)^2 + (2/3)^2 + (-1/3)^2 = 0.667$$ |
| + | :$$ \Rightarrow \hspace{0.3cm} s_{22} = \sqrt{0.667} = 0.816,\hspace{0.3cm} | ||
| + | \varphi_2(t) = \theta_2(t)/s_{22} = (0.408,\ 0.816,\ -0.408)\hspace{0.05cm}. $$ | ||
| − | : | + | *The inner products between $s_3(t)$ with $\varphi_1(t)$ or $\varphi_2(t)$ give the following results: |
| + | :$$s_{31} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.577) + 0.5 \cdot (-0.577)- 0.5 \cdot (-0.577)= 0.289$$ | ||
| + | :$$s_{32} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.408) + 0.5 \cdot (+0.816)- 0.5 \cdot (-0.408)= 0.816$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}\theta_3(t) = s_3(t) - 0.289 \cdot \varphi_1(t)- 0.816 \cdot \varphi_2(t) = 0\hspace{0.05cm}.$$ | ||
| − | : | + | *This means: The green function $s_3(t)$ does not yield a new basis function $\varphi_3(t)$, in contrast to the function $s_4(t)$. The numerical results for this can be taken from the graph.}} |
| − | == | + | == Basis functions of complex time signals == |
<br> | <br> | ||
| − | In | + | In Communications Engineering, one often has to deal with complex time functions, |
| − | * | + | *not because there are complex signals in reality, but<br> |
| − | * | + | *because the description of a band-pass signal in the equivalent low-pass range leads to complex signals.<br><br> |
| − | + | The determination of the $N \le M$ '''complex-valued basis functions''' $\xi_k(t)$ from the $M$ complex signals $s_i(t)$ can also be done using the [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#The_Gram-Schmidt_process| "Gram–Schmidt process"]], but it must now be taken into account that the inner product of two complex signals $x(t)$ and $y(t)$ must be calculated as follows: | |
| − | + | :$$< \hspace{-0.1cm}x(t), \hspace{0.1cm}y(t)\hspace{-0.1cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}x(t) \cdot y^{\star}(t)\,d \it t | |
| − | : | + | \hspace{0.05cm}.$$ |
| − | \hspace{0.05cm}. | ||
| − | |||
| − | |||
| − | : | + | The corresponding equations are now with $i = 1, \text{..}. , M$ and $k = 1, \text{..}. , N$: |
| − | ,\hspace{0.2cm}\xi_k(t) \in {\cal C} \hspace{0.05cm}, | + | :$$s_i(t) = \sum\limits_{k = 1}^{N}s_{ik} \cdot \xi_k(t),\hspace{0.2cm}s_i(t) \in {\cal C},\hspace{0.2cm}s_{ik} \in {\cal C} |
| + | ,\hspace{0.2cm}\xi_k(t) \in {\cal C} \hspace{0.05cm},$$ | ||
| − | : | + | :$$< \hspace{-0.1cm}\xi_k(t),\hspace{0.1cm} \xi_j(t)\hspace{-0.1cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}\xi_k(t) \cdot \xi_j^{\star}(t)\,d \it t |
= {\rm \delta}_{ik} = | = {\rm \delta}_{ik} = | ||
\left\{ \begin{array}{c} 1 \\ | \left\{ \begin{array}{c} 1 \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c}{\rm | + | \begin{array}{*{1}c}{\rm if}\hspace{0.25cm} k = j |
| − | \\ {\rm | + | \\ {\rm if}\hspace{0.25cm} k \ne j \\ \end{array}\hspace{0.05cm}.$$ |
| + | |||
| + | Of course, any complex quantity can also be expressed by two real quantities, namely real part and imaginary part. Thus, the following equations are obtained here: | ||
| + | :$$s_{i}(t) = s_{{\rm I}\hspace{0.02cm}i}(t) + {\rm j} \cdot s_{{\rm Q}\hspace{0.02cm}i}(t), | ||
| + | \hspace{0.2cm} s_{{\rm I}\hspace{0.02cm}i}(t) = {\rm Re}\big [s_{i}(t)\big], \hspace{0.2cm} s_{{\rm Q}\hspace{0.02cm}i}(t) = {\rm Im} \big [s_{i}(t)\big ],$$ | ||
| − | + | :$$\xi_{k}(t) = \varphi_k(t) + {\rm j} \cdot \psi_k(t), | |
| + | \hspace{0.2cm} \varphi_k(t) = {\rm Re}\big [\xi_{k}(t)\big ], \hspace{0.2cm} \psi_k(t) = {\rm Im} \big [\xi_{k}(t)\big ],$$ | ||
| − | : | + | :$$\hspace{0.35cm} s_{ik} = s_{{\rm I}\hspace{0.02cm}ik} + {\rm j} \cdot s_{{\rm Q}\hspace{0.02cm}ik}, |
| − | \hspace{0.2cm} s_{{\rm I} | + | \hspace{0.2cm} s_{{\rm I}ik} = {\rm Re} \big [s_{ik}\big ], \hspace{0.2cm} s_{{\rm Q}ik} = {\rm Im} \big [s_{ik}\big ],$$ |
| − | : | + | :$$ \hspace{0.35cm} s_{{\rm I}\hspace{0.02cm}ik} ={\rm Re}\big [\hspace{0.01cm} < \hspace{-0.1cm} s_i(t), \hspace{0.15cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm}\big ], \hspace{0.2cm}s_{{\rm Q}\hspace{0.02cm}ik} = {\rm Re}\big [\hspace{0.01cm} < \hspace{-0.1cm} s_i(t), \hspace{0.15cm}{\rm j} \cdot \psi_k(t) \hspace{-0.1cm} > \hspace{0.1cm}\big ] |
| − | \hspace{0.2cm} \ | + | \hspace{0.05cm}. $$ |
| − | + | The nomenclature arises from the main application for complex basis functions, namely [[Modulation_Methods/Quadrature_Amplitude_Modulation#General_description_and_signal_space_allocation|"quadrature amplitude modulation"]] $\rm (QAM)$. | |
| − | + | *The subscript "I" stands for inphase component and indicates the real part, | |
| − | + | *while the quadrature component (imaginary part) is indicated by the index "Q".<br> | |
| − | |||
| − | |||
| − | + | To avoid confusion with the imaginary unit "$\rm j$", here the complex basis functions $\xi_{k}(t)$ were induced with $k$ and not with $j$.<br> | |
| − | == Dimension | + | == Dimension of the basis functions == |
<br> | <br> | ||
| − | + | In baseband transmission, the possible transmitted signals $($considering only one symbol duration$)$ are | |
| − | : | + | :$$s_i(t) = a_i \cdot g_s(t), \hspace{0.2cm} i = 0, \text{...}\hspace{0.05cm} , M-1,$$ |
| − | + | where $g_s(t)$ indicates the "basic transmission pulse" and the $a_i$ were denoted in the first three main chapters as the possible "amplitude coefficients". It should be noted that from now on the values $0$ to $M-1$ are assumed for the indexing variable $i$. <br> | |
| − | + | According to the description of this chapter, this is a one-dimensional modulation process $(N = 1)$, regardless of the level number $M$. | |
| − | |||
| − | :: | + | {{BlaueBox|TEXT= |
| + | $\text{In the case of baseband transmission:}$ | ||
| + | *The basis function $\varphi_1(t)$ is equal to the energy-normalized basic transmission pulse $g_s(t)$: | ||
| + | :$$\varphi_1(t) ={g_s(t)}/{\sqrt{E_{gs} } } \hspace{0.3cm}{\rm with}\hspace{0.3cm} | ||
E_{gs} = \int_{-\infty}^{+\infty}g_s^2(t)\,d \it t | E_{gs} = \int_{-\infty}^{+\infty}g_s^2(t)\,d \it t | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}.$$ |
| + | |||
| + | *The dimensionless amplitude coefficients $a_i$ are to be converted into the signal space points $s_i$ which have the unit "root of energy".<br>}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 3:}$ | ||
| + | The graph shows one-dimensional signal space constellations $(N=1)$ for baseband transmission, viz. | ||
| + | [[File:EN_Dig_T_4_1_S5_neu.png|right|frame|One-dimensional modulation processes|class=fit]] | ||
| + | # binary unipolar (top) ⇒ $M = 2$, | ||
| + | # binary bipolar (center) ⇒ $M = 2$, and | ||
| + | # quaternary bipolar (bottom) ⇒ $M = 4$. | ||
| − | |||
| − | + | The graph simultaneously describes the one-dimensional carrier frequency systems | |
| + | # [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#On.E2.80.93off_keying_.282.E2.80.93ASK.29|"Two-level Amplitude Shift Keying"]] $\text{(2–ASK)}$, | ||
| + | # [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Binary_phase_shift_keying_.28BPSK.29|"Binary Phase Shift Keying"]] $\text{(BPSK)}$, | ||
| + | # [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#M.E2.80.93level_amplitude_shift_keying_.28M.E2.80.93ASK.29|"Four-level Amplitude Shift Keying"]] $\text{(4–ASK)}$.<br> | ||
| − | + | <u>Note:</u> | |
| + | *The signals $s_i(t)$ and the basis function $\varphi_1(t)$ always refer to the equivalent low-pass range. | ||
| − | * | + | *In the band-pass region, $\varphi_1(t)$ is a harmonic oscillation limited to the time domain $0 \le t \le T$. |
| − | * | + | *In the graph on the right, the two or four possible signals $s_i(t)$ are given for the example "rectangular pulse". |
| − | = | + | *From this, one can see the relationship between pulse amplitude $A$ and signal energy $E = A^2 \cdot T$. }} |
| − | <br> | + | <br clear =all> |
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Example 4:}$ | |
| − | + | The two-dimensional modulation processes include: | |
| − | + | [[File:P ID1992 Dig T 4 1 S5b version1.png|right|frame|Two-dimensional signal space constellations for multi-level PSK and QAM|class=fit]] | |
| + | #[[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Multi-level_phase.E2.80.93shift_keying_.28M.E2.80.93PSK.29|"<i>M</i>–level Phase Shift Keying"]] (M–PSK),<br> | ||
| + | #[[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Quadrature_amplitude_modulation_.28M-QAM.29|"Quadrature amplitude modulation"]] (4–QAM, 16–QAM, ...),<br> | ||
| + | #[[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Binary_frequency_shift_keying_.282.E2.80.93FSK.29|"Binary (orthogonal) frequency shift keying"]] (2–FSK).<br> | ||
| − | |||
| − | + | In general, for orthogonal FSK the number $N$ of basis functions $\varphi_k(t)$ is equal to the number $M$ of possible transmitted signals $s_i(t)$ ⇒ $N=2$ is only possible for $M=2$. | |
| − | + | The graph describes two-dimensional modulation processes in the band-pass (left) and in the equivalent low-pass range (right): | |
| + | *The left graph shows "8–PSK". If we restrict us to the red points only ⇒ "4–PSK" is present ("Quaternary Phase Shift Keying", QPSK).<br> | ||
| − | + | *The right-hand diagram refers to "16–QAM" or – if only the signal space points outlined in red are considered – to "4–QAM". | |
| + | |||
| + | *A comparison of the two images with appropriate axis scaling shows that "4–QAM" is identical to "QPSK".<br> | ||
| − | + | *When considered as a band-pass system, the basis function $\varphi_1(t)$ is cosinusoidal and $\varphi_2(t)$ $($minus$)$ sinusoidal – compare [[Aufgaben:Exercise_4.2:_AM/PM_Oscillations|"Exercise 4.2"]].<br> | |
| − | |||
| − | * | + | *On the other hand, after transforming the QAM systems into the equivalent low-pass range, $\varphi_1(t)$ is equal to the energy-normalized $($i.e., with energy "1"$)$ basic transmission pulse $g_s(t)$, while $\varphi_2(t)={\rm j} \cdot \varphi_1(t)$. For more details, please refer to [[Aufgaben:Exercise_4.2Z:_Eight-step_Phase_Shift_Keying|"Exercise 4.2Z"]].}}<br> |
| + | <br> | ||
| − | == | + | == Exercises for the chapter == |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.1:_About_the_Gram-Schmidt_Process|Exercise 4.1: About the Gram-Schmidt Method]] |
| − | [[ | + | [[Aufgaben:Exercise_4.1Z:_Other_Basis_Functions|Exercise 4.1Z: Other Basis Functions]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_4.2:_AM/PM-Schwingungen|Exercise 4.2: AM/PM Oscillations]] |
| − | [[ | + | [[Aufgaben:Exercise_4.2Z:_Eight-level_Phase_Shift_Keying|Exercise 4.2Z: Eight-level Phase Shift Keying]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_4.3:_Unterschiedliche_Frequenzen|Exercise 4.3: Different Frequencies]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
Latest revision as of 12:11, 5 April 2023
Contents
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
The fourth main chapter provides an abstract description of digital signal transmission, which is based on basis functions and signal space constellations. This makes it possible to treat very different configurations – for example band-pass systems and those for the baseband – in a uniform way. The optimal receiver in each case has the same structure in all cases.
The following are dealt with in detail:
- The meaning of »basis functions« and finding them using the »Gram-Schmidt process«,
- the »structure of the optimal receiver« for baseband transmission,
- the »theorem of irrelevance« and its importance for the derivation of optimal detectors,
- the »optimal receiver for the AWGN channel« and implementation aspects,
- the system description by »complex or $N$–dimensional Gaussian noise«,
- the »error probability calculation and approximation« under otherwise ideal conditions,
- the application of the signal space description to »carrier frequency systems«,
- the different results for »OOK, M-ASK, M-PSK, M-QAM and M-FSK«,
- the different results for »coherent and non-coherent demodulation«.
Almost all results of this chapter have already been derived in previous sections. However, the approach is fundamentally new:
- In the $\rm LNTwww$ book "Modulation Methods" and in the first three chapters of this book, the specific system properties were already taken into account in the derivations – for example, whether the digital signal is transmitted in baseband or whether digital amplitude, frequency or phase modulation is present.
- Here the systems are to be abstracted in such a way that they can be treated uniformly. The optimal receiver in each case has the same structure in all cases, and the error probability can also be specified for non-Gaussian distributed noise.
It should be noted that this rather global approach means that certain system deficiencies can only be recorded very imprecisely, such as
- the influence of a non-optimal receiver filter on the error probability,
- an incorrect threshold $($threshold drift$)$, or
- phase jitter $($fluctuations in sampling times$)$.
In particular in the presence of intersymbol interference, the procedure should therefore continue in accordance with the third main chapter.
The description is based on the script [KöZ08][1] by Ralf Kötter and Georg Zeitler, which is closely based on the textbook [WJ65][2]. Gerhard Kramer, who has held the chair at the LNT since 2010, treats the same topic with very similar nomenclature in his lecture [Kra17][3]. In order not to make reading unnecessarily difficult for our own students at TU Munich, we stick to this nomenclature as far as possible, even if it deviates from other $\rm LNTwww$ chapters.
Nomenclature in the fourth chapter
Compared to the other $\rm LNTwww$ chapters, the following nomenclature changes arise here:
- The "message" to be transmitted is an integer value $m \in \{m_i\}$ with $i = 0$, ... , $M-1$, where $M$ specifies the "symbol set size".
If it simplifies the description, $i = 1$, ... , $M$ is induced.
- The result of the decision process at the receiver is also an integer with the same symbol alphabet as at the transmitter.
This result is also referred to as the "estimated value":
- $$\hat{m} \in \{m_i \}, \hspace{0.2cm} i = 0, 1, \text{...}\hspace{0.05cm} , M-1\hspace{0.2cm} ({\rm or}\,\,i = 1, 2, \text{...}\hspace{0.05cm}, M) \hspace{0.05cm}.$$
- The "symbol error probability" $\rm Pr(symbol\hspace{0.15cm} error)$ or $p_{\rm S}$ is usually referred to as follows in this main chapter:
- $${\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) = 1 - {\rm Pr} ({\cal C}), \hspace{0.4cm}\text{complementary event:}\hspace{0.2cm} {\rm Pr} ({\cal C}) = {\rm Pr} ( \hat{m} = m) \hspace{0.05cm}.$$
- In a "probability density function" $\rm (PDF)$, a distinction is made between the "random variable" ⇒ $r$ and the "realization" ⇒ $\rho$ according to $p_r(\rho)$.
Formerly, $f_r(r)$ was used for this PDF.
- With the notation $p_r(\rho)$, $r$ and $\rho$ are scalars. On the other hand, if random variable and realization are vectors (of suitable length), this is expressed in bold type: $p_{ \boldsymbol{ r}}(\boldsymbol{\rho})$ with the vectors $ \boldsymbol{ r}$ and $\boldsymbol{\rho}$.
- In order to avoid confusion with energy values, the "threshold value is" now called $G$ instead of $E$. This is mainly referred to as the "decision threshold" in this chapter.
- Based on the two real and energy-limited time functions $x(t)$ and $y(t)$, the "inner product" is:
- $$<\hspace{-0.1cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.1cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t \hspace{0.05cm}.$$
- This results in the "Euclidean norm" or "2–norm" $($or "norm" for short$)$:
- $$||x(t) || = \sqrt{<\hspace{-0.1cm}x(t), \hspace{0.05cm}x(t) \hspace{-0.1cm}>} \hspace{0.05cm}.$$
- Compared to the script [KöZ08][1], the naming differs as follows:
- The probability of the event $E$ is ${\rm Pr}(E)$ instead of $P(E)$.
This nomenclature change was also made because in some equations "probabilities" and "powers" appear together. - Band–pass signals are still marked with the index "BP" and not with a tilde as in [KöZ08][1].
The corresponding "low-pass signal" is (usually) provided with the index "TP" $($from German "Tiefpass"$)$.
Orthonormal basis functions
In this chapter, we assume a set $\{s_i(t)\}$ of possible transmitted signals that are uniquely assigned to the possible messages $m_i$. With $i = 1$, ... , $M$ holds:
- $$m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: \hspace{0.3cm} m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.$$
For what follows, we further assume that the $M$ signals $s_i(t)$ are "energy-limited", which usually means at the same time that they are of finite duration.
$\text{Theorem:}$ Any set $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ of energy-limited signals can be evolved into $N \le M$ orthonormal basis functions $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$. It holds:
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$
- In each case, two basis functions $\varphi_j(t)$ and $\varphi_k(t)$ must be orthonormal to each other, that is, it must hold
$(\delta_{jk}$ is called "Kronecker symbol" or "Kronecker delta"$)$:
- $$<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm if}\hspace{0.1cm}j = k \\ {\rm if}\hspace{0.1cm} j \ne k \\ \end{array} \hspace{0.05cm}.$$
Here, the parameter $N$ indicates how many basis functions $\varphi_j(t)$ are needed to represent the $M$ possible transmitted signals. In other words: $N$ is the "dimension of the vector space" spanned by the $M$ signals. Here, the following holds:
- If $N = M$, all transmitted signals are orthogonal to each other.
- They are not necessarily orthonormal, i.e. the energies $E_i = <\hspace{-0.1cm}s_i(t), \hspace{0.05cm}s_i(t) \hspace{-0.1cm}>$ may well be unequal to one.
- $N < M$ arises when at least one signal $s_i(t)$ can be represented as linear combination of basis functions $\varphi_j(t)$ that have resulted from other signals $s_j(t) \ne s_i(t)$.
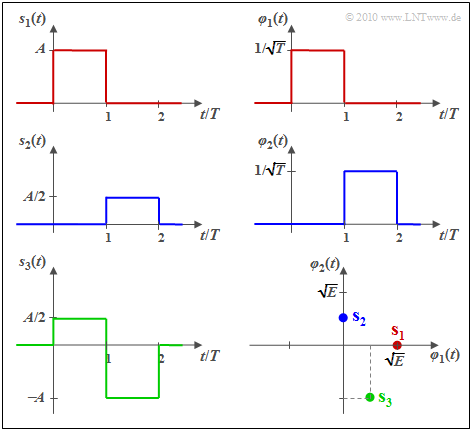
$\text{Example 1:}$ We consider $M = 3$ energy-limited signals according to the graph. One recognizes immediately:
- The signals $s_1(t)$ and $s_2(t)$ are orthogonal to each other.
- The energies are $E_1 = A^2 \cdot T = E$ and $E_2 = (A/2)^2 \cdot T = E/4$.
- The basis functions $\varphi_1(t)$ and $\varphi_2(t)$ are equal in form to $s_1(t)$ and $s_2(t)$, resp., and both have energy one:
- $$\varphi_1(t)=\frac{s_1(t)}{\sqrt{E_1} } = \frac{s_1(t)}{\sqrt{A^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_1(t)}{A}$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},$$
- $$\varphi_2(t) =\frac{s_2(t)}{\sqrt{E_2} } = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = {\sqrt{E} }/{2}\hspace{0.05cm}.$$
- $s_3(t)$ can be expressed by the previously determined basis functions $\varphi_1(t)$, $\varphi_2(t)$:
- $$s_3(t) =s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm} s_{31} = {A}/{2} \cdot \sqrt {T}= {\sqrt{E} }/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.$$
⇒ In the lower right image, the signals are shown in a two-dimensional representation
- with the basis functions $\varphi_1(t)$ and $\varphi_2(t)$ as axes,
- where $E = A^2 \cdot T$ and the relation to the other graphs can be seen by the coloring.
⇒ The vectorial representatives of the signals $s_1(t)$, $s_2(t)$ and $s_3(t)$ in the two-dimensional vector space can be read from this sketch as follows:
- $$\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), $$
- $$\mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), $$
- $$\mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.$$
The Gram-Schmidt process
In $\text{Example 1}$ in the last section, the specification of the two orthonormal basis functions $\varphi_1(t)$ and $\varphi_2(t)$ was very easy, because they were of the same form as $s_1(t)$ and $s_2(t)$, respectively. The "Gram-Schmidt process" finds the basis functions $\varphi_1(t)$, ... , $\varphi_N(t)$ for arbitrary predefinable signals $s_1(t)$, ... , $s_M(t)$, as follows:
- The first basis function $\varphi_1(t)$ is always equal in form to $s_1(t)$. It holds:
- $$\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm or }}\hspace{0.2cm} j \ge 2 \hspace{0.05cm}.$$
- It is now assumed that from the signals $s_1(t)$, ... , $s_{k-1}(t)$ the basis functions $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ have been calculated $(n \le k)$. Then, using $s_k(t)$, we compute the auxiliary function
- $$\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm with}\hspace{0.4cm} s_{kj} = \hspace{0.1cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.1cm} >, \hspace{0.2cm} j = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm}, n-1\hspace{0.05cm}.$$
- If $\theta_k(t) \equiv 0$ ⇒ $||\theta_k(t)|| = 0$, then $s_k(t)$ does not yield a new basis function. Rather, $s_k(t)$ can then be expressed by the $n-1$ basis functions $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ already found before:
- $$s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.$$
- A new basis function $($namely, the $n$–th$)$ results if $||\theta_k(t)|| \ne 0$:
- $$\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.$$
This process is continued until all $M$ signals have been considered. Then all $N \le M$ orthonormal basis functions $\varphi_j(t)$ have been found. The special case $N = M$ arises only if all $M$ signals are linearly independent.
- This process is now illustrated by an example.
- We also refer to the (German language) HTML5/JavaScript applet "Das Gram-Schmidt-Verfahren" ⇒ "Gram–Schmidt process".
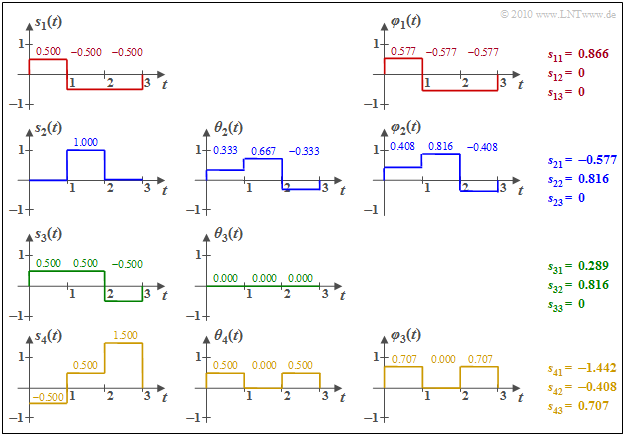
$\text{Example 2:}$ We consider the $M = 4$ energy-limited signals $s_1(t)$, ... , $s_4(t)$. To simplify the calculations, both amplitude and time are normalized here.
One can see from these sketches:
- The basis function $\varphi_1(t)$ is equal in form to $s_1(t)$. Because $E_1 = \vert \vert s_1(t) \vert \vert ^3 = 3 \cdot 0.5^2 = 0.75$, we get $s_{11} = \vert \vert s_1(t) \vert \vert = 0.866$. $\varphi_1(t)$ itself has section-wise values $\pm 0.5/0.866 = \pm0.577$.
- To calculate the auxiliary function $\theta_2(t)$, we compute
- $$s_{21} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.05cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0 \cdot (+0.577) + 1 \cdot (-0.577)+ 0 \cdot (-0.577)= -0.577$$
- $$ \Rightarrow \hspace{0.3cm}\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = (0.333, 0.667, -0.333) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\vert \vert \theta_2(t) \vert \vert^2 = (1/3)^2 + (2/3)^2 + (-1/3)^2 = 0.667$$
- $$ \Rightarrow \hspace{0.3cm} s_{22} = \sqrt{0.667} = 0.816,\hspace{0.3cm} \varphi_2(t) = \theta_2(t)/s_{22} = (0.408,\ 0.816,\ -0.408)\hspace{0.05cm}. $$
- The inner products between $s_3(t)$ with $\varphi_1(t)$ or $\varphi_2(t)$ give the following results:
- $$s_{31} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.577) + 0.5 \cdot (-0.577)- 0.5 \cdot (-0.577)= 0.289$$
- $$s_{32} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.408) + 0.5 \cdot (+0.816)- 0.5 \cdot (-0.408)= 0.816$$
- $$\Rightarrow \hspace{0.3cm}\theta_3(t) = s_3(t) - 0.289 \cdot \varphi_1(t)- 0.816 \cdot \varphi_2(t) = 0\hspace{0.05cm}.$$
- This means: The green function $s_3(t)$ does not yield a new basis function $\varphi_3(t)$, in contrast to the function $s_4(t)$. The numerical results for this can be taken from the graph.
Basis functions of complex time signals
In Communications Engineering, one often has to deal with complex time functions,
- not because there are complex signals in reality, but
- because the description of a band-pass signal in the equivalent low-pass range leads to complex signals.
The determination of the $N \le M$ complex-valued basis functions $\xi_k(t)$ from the $M$ complex signals $s_i(t)$ can also be done using the "Gram–Schmidt process", but it must now be taken into account that the inner product of two complex signals $x(t)$ and $y(t)$ must be calculated as follows:
- $$< \hspace{-0.1cm}x(t), \hspace{0.1cm}y(t)\hspace{-0.1cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}x(t) \cdot y^{\star}(t)\,d \it t \hspace{0.05cm}.$$
The corresponding equations are now with $i = 1, \text{..}. , M$ and $k = 1, \text{..}. , N$:
- $$s_i(t) = \sum\limits_{k = 1}^{N}s_{ik} \cdot \xi_k(t),\hspace{0.2cm}s_i(t) \in {\cal C},\hspace{0.2cm}s_{ik} \in {\cal C} ,\hspace{0.2cm}\xi_k(t) \in {\cal C} \hspace{0.05cm},$$
- $$< \hspace{-0.1cm}\xi_k(t),\hspace{0.1cm} \xi_j(t)\hspace{-0.1cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}\xi_k(t) \cdot \xi_j^{\star}(t)\,d \it t = {\rm \delta}_{ik} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c}{\rm if}\hspace{0.25cm} k = j \\ {\rm if}\hspace{0.25cm} k \ne j \\ \end{array}\hspace{0.05cm}.$$
Of course, any complex quantity can also be expressed by two real quantities, namely real part and imaginary part. Thus, the following equations are obtained here:
- $$s_{i}(t) = s_{{\rm I}\hspace{0.02cm}i}(t) + {\rm j} \cdot s_{{\rm Q}\hspace{0.02cm}i}(t), \hspace{0.2cm} s_{{\rm I}\hspace{0.02cm}i}(t) = {\rm Re}\big [s_{i}(t)\big], \hspace{0.2cm} s_{{\rm Q}\hspace{0.02cm}i}(t) = {\rm Im} \big [s_{i}(t)\big ],$$
- $$\xi_{k}(t) = \varphi_k(t) + {\rm j} \cdot \psi_k(t), \hspace{0.2cm} \varphi_k(t) = {\rm Re}\big [\xi_{k}(t)\big ], \hspace{0.2cm} \psi_k(t) = {\rm Im} \big [\xi_{k}(t)\big ],$$
- $$\hspace{0.35cm} s_{ik} = s_{{\rm I}\hspace{0.02cm}ik} + {\rm j} \cdot s_{{\rm Q}\hspace{0.02cm}ik}, \hspace{0.2cm} s_{{\rm I}ik} = {\rm Re} \big [s_{ik}\big ], \hspace{0.2cm} s_{{\rm Q}ik} = {\rm Im} \big [s_{ik}\big ],$$
- $$ \hspace{0.35cm} s_{{\rm I}\hspace{0.02cm}ik} ={\rm Re}\big [\hspace{0.01cm} < \hspace{-0.1cm} s_i(t), \hspace{0.15cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm}\big ], \hspace{0.2cm}s_{{\rm Q}\hspace{0.02cm}ik} = {\rm Re}\big [\hspace{0.01cm} < \hspace{-0.1cm} s_i(t), \hspace{0.15cm}{\rm j} \cdot \psi_k(t) \hspace{-0.1cm} > \hspace{0.1cm}\big ] \hspace{0.05cm}. $$
The nomenclature arises from the main application for complex basis functions, namely "quadrature amplitude modulation" $\rm (QAM)$.
- The subscript "I" stands for inphase component and indicates the real part,
- while the quadrature component (imaginary part) is indicated by the index "Q".
To avoid confusion with the imaginary unit "$\rm j$", here the complex basis functions $\xi_{k}(t)$ were induced with $k$ and not with $j$.
Dimension of the basis functions
In baseband transmission, the possible transmitted signals $($considering only one symbol duration$)$ are
- $$s_i(t) = a_i \cdot g_s(t), \hspace{0.2cm} i = 0, \text{...}\hspace{0.05cm} , M-1,$$
where $g_s(t)$ indicates the "basic transmission pulse" and the $a_i$ were denoted in the first three main chapters as the possible "amplitude coefficients". It should be noted that from now on the values $0$ to $M-1$ are assumed for the indexing variable $i$.
According to the description of this chapter, this is a one-dimensional modulation process $(N = 1)$, regardless of the level number $M$.
$\text{In the case of baseband transmission:}$
- The basis function $\varphi_1(t)$ is equal to the energy-normalized basic transmission pulse $g_s(t)$:
- $$\varphi_1(t) ={g_s(t)}/{\sqrt{E_{gs} } } \hspace{0.3cm}{\rm with}\hspace{0.3cm} E_{gs} = \int_{-\infty}^{+\infty}g_s^2(t)\,d \it t \hspace{0.05cm}.$$
- The dimensionless amplitude coefficients $a_i$ are to be converted into the signal space points $s_i$ which have the unit "root of energy".
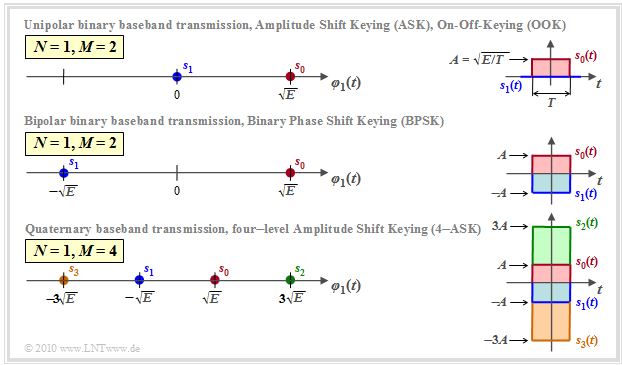
$\text{Example 3:}$ The graph shows one-dimensional signal space constellations $(N=1)$ for baseband transmission, viz.
- binary unipolar (top) ⇒ $M = 2$,
- binary bipolar (center) ⇒ $M = 2$, and
- quaternary bipolar (bottom) ⇒ $M = 4$.
The graph simultaneously describes the one-dimensional carrier frequency systems
- "Two-level Amplitude Shift Keying" $\text{(2–ASK)}$,
- "Binary Phase Shift Keying" $\text{(BPSK)}$,
- "Four-level Amplitude Shift Keying" $\text{(4–ASK)}$.
Note:
- The signals $s_i(t)$ and the basis function $\varphi_1(t)$ always refer to the equivalent low-pass range.
- In the band-pass region, $\varphi_1(t)$ is a harmonic oscillation limited to the time domain $0 \le t \le T$.
- In the graph on the right, the two or four possible signals $s_i(t)$ are given for the example "rectangular pulse".
- From this, one can see the relationship between pulse amplitude $A$ and signal energy $E = A^2 \cdot T$.
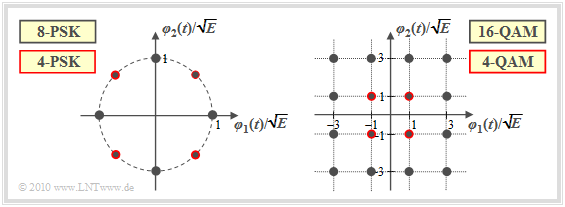
$\text{Example 4:}$ The two-dimensional modulation processes include:
- "M–level Phase Shift Keying" (M–PSK),
- "Quadrature amplitude modulation" (4–QAM, 16–QAM, ...),
- "Binary (orthogonal) frequency shift keying" (2–FSK).
In general, for orthogonal FSK the number $N$ of basis functions $\varphi_k(t)$ is equal to the number $M$ of possible transmitted signals $s_i(t)$ ⇒ $N=2$ is only possible for $M=2$.
The graph describes two-dimensional modulation processes in the band-pass (left) and in the equivalent low-pass range (right):
- The left graph shows "8–PSK". If we restrict us to the red points only ⇒ "4–PSK" is present ("Quaternary Phase Shift Keying", QPSK).
- The right-hand diagram refers to "16–QAM" or – if only the signal space points outlined in red are considered – to "4–QAM".
- A comparison of the two images with appropriate axis scaling shows that "4–QAM" is identical to "QPSK".
- When considered as a band-pass system, the basis function $\varphi_1(t)$ is cosinusoidal and $\varphi_2(t)$ $($minus$)$ sinusoidal – compare "Exercise 4.2".
- On the other hand, after transforming the QAM systems into the equivalent low-pass range, $\varphi_1(t)$ is equal to the energy-normalized $($i.e., with energy "1"$)$ basic transmission pulse $g_s(t)$, while $\varphi_2(t)={\rm j} \cdot \varphi_1(t)$. For more details, please refer to "Exercise 4.2Z".
Exercises for the chapter
Exercise 4.1: About the Gram-Schmidt Method
Exercise 4.1Z: Other Basis Functions
Exercise 4.2: AM/PM Oscillations
Exercise 4.2Z: Eight-level Phase Shift Keying
Exercise 4.3: Different Frequencies
References
- ↑ 1.0 1.1 1.2 Kötter, R., Zeitler, G.: Lecture notes, Institute for Communications Engineering, Technical University of Munich, 2008.
- ↑ Wozencraft, J. M.; Jacobs, I. M.: Principles of Communication Engineering. New York: John Wiley & Sons, 1965.
- ↑ Kramer, G.: Nachrichtentechnik 2. Lecture notes, Institute for Communications Engineering, Technical University of Munich, 2017.