Difference between revisions of "Linear and Time Invariant Systems/Some Low-Pass Functions in Systems Theory"
m (Text replacement - "[[Lineare_zeitinvariante_Systeme/" to "[[Linear_and_Time_Invariant_Systems/") |
|||
| (128 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Basics of System Theory |
| − | |Vorherige Seite= | + | |Vorherige Seite=System_Description_in_Time_Domain |
| − | |Nächste Seite= | + | |Nächste Seite=Classification_of_the_Distortions |
}} | }} | ||
| − | == | + | ==General remarks== |
<br> | <br> | ||
| − | + | All low-pass functions described in the next sections have the following properties: | |
| − | * | + | *The frequency response $H(f)$ is real and even so that according to the [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|$\text{Assignment Theorem}$]] the associated impulse response $h(t)$ is always real and even, too. |
| − | * | + | |
| − | * | + | *Thus, it is obvious that the systems considered here are non-causal and hence not realizable. The description of causal systems is given in the chapter [[Linear_and_Time_Invariant_Systems/Folgerungen_aus_dem_Zuordnungssatz|»Description of Causal Realizable Systems«]] of this book. |
| − | * | + | |
| + | *The advantage of these »system theoretical filter functions« is the simple description by at most two parameters such that the filter influence can be represented in a transparent way. | ||
| + | |||
| + | *The most important frequency response parameter is the »'''equivalent bandwidth'''« according to the definition via the equal-area rectangle: | ||
:$$\Delta f = \frac{1}{H(f=0)}\cdot \int_{-\infty}^{+\infty}H(f) \hspace{0.15cm} {\rm d}f.$$ | :$$\Delta f = \frac{1}{H(f=0)}\cdot \int_{-\infty}^{+\infty}H(f) \hspace{0.15cm} {\rm d}f.$$ | ||
| − | * | + | *According to the so-called [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|»Reciprocity Theorem of time duration and bandwidth«]] the »'''equivalent duration of the impulse response'''« is thus fixed, which is also defined via the equal-area rectangle: |
:$$\Delta t = \frac{1}{h(t=0)}\cdot \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm} {\rm d}t = \frac{1}{\Delta f}.$$ | :$$\Delta t = \frac{1}{h(t=0)}\cdot \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm} {\rm d}t = \frac{1}{\Delta f}.$$ | ||
| − | * | + | *The direct signal $\rm (DC)$ transmission factor is always assumed to be $H(f = 0) = 1$ unless explicitly stated otherwise. |
| − | * | + | |
| + | *From every low-pass function corresponding high-pass functions can be derived as shown in the section [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Derivation_of_system_theoretical_high-pass_functions|»Derivation of system theoretical high-pass functions«]]. | ||
| − | == | + | ==Ideal low-pass filter – Rectangular-in-frequency== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | An '''»ideal low-pass filter«''' is on hand if its frequency response has the following rectangular shape: | |
| − | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ 0.5 \\\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} \text { | + | :$$H(f) = H_{\rm RLP}(f) =\left\{ \begin{array}{l} \hspace{0.25cm}1 \\ 0.5 \\\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} \text {for} \\ \text {for} \\ \text {for} \\ \end{array}\begin{array}{*{20}c}{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert< \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert = \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert > \Delta f/2.} \\\end{array}$$ |
| − | + | #We sometimes also use the term »rectangular low-pass filter« $\rm (RLP)$. | |
| + | #Here $Δf$ denotes the »system theoretical bandwidth«. | ||
| + | #$f_{\rm G}=Δf/2$ denotes the »cut-off frequency« $($German: "Grenzfrequenz" ⇒ subscript $\rm G)$. }} | ||
| + | |||
| + | |||
| + | [[File:P_ID842__LZI_T_1_3_S2_neu.png |right|frame| Ideal low-pass filter: Frequency response and impulse response|class=fit]] | ||
| + | The graph shows such an ideal low-pass filter in the frequency and time domain. | ||
| + | |||
| + | The following can be concluded from these curves: | ||
| + | |||
| + | *Due to the abrupt, infinitely steep roll-off the »3 dB cut-off frequency« ⇒ <br>$f_{\rm G}$ is here exactly half the »system theoretic bandwidth« $Δf$. | ||
| + | |||
| + | *All spectral components with $f \lt f_{\rm G}$ are transmitted undistorted ⇒ »pass band«. | ||
| + | |||
| + | *All components with $f \gt f_{\rm G}$ are completely suppressed ⇒ »stop band«. | ||
| + | |||
| + | *By definition, $H(f) = 0.5$ holds for $f = \pm f_{\rm G}$. | ||
| − | + | '''Description of the ideal low-pass filter in the time domain:''' | |
| + | *According to the inverse Fourier transform the »impulse response« $($right diagram$)$: | ||
| + | :$$h(t) = h_{\rm RLP}(t) =\Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t)\hspace{0.55cm}{\rm{with}}\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x},\hspace{0.5cm}{\rm or}$$ | ||
| + | :::$$h_{\rm RLP}(t) =\Delta f \cdot {\rm sinc}(\Delta f \cdot t)\hspace{0.7cm}{\rm{with}}\hspace{0.7cm}{\rm sinc}(x) ={\sin(\pi x)}/{(\pi x)}.$$ | ||
| + | *$h(t)$ extended to infinity on both sides and exhibits equidistant zero-crossings at an interval of $Δt = 1/ Δf$. | ||
| − | + | *The asymptotic decay is inversely proportional to time $|t|$: | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:$$|h(t)| = \frac{\Delta f}{\pi \cdot \Delta f \cdot |t|} \cdot \left |{\rm sin}(\pi \cdot \Delta f\cdot t )\right | \le \frac{1}{\pi \cdot |t|}.$$ | :$$|h(t)| = \frac{\Delta f}{\pi \cdot \Delta f \cdot |t|} \cdot \left |{\rm sin}(\pi \cdot \Delta f\cdot t )\right | \le \frac{1}{\pi \cdot |t|}.$$ | ||
| − | * | + | *It follows that the impulse response is certainly less than $1‰$ of the impulse maximum only for times $t \gt t_{1‰} = 318 \cdot \Delta t$. |
| − | * | + | |
| + | *The step response $\sigma(t)$ is obtained from the impulse response by integration and is: | ||
:$${\sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{2} + \frac{1}{\pi} \cdot {\rm Si}(\pi \cdot\Delta f \cdot t ).$$ | :$${\sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{2} + \frac{1}{\pi} \cdot {\rm Si}(\pi \cdot\Delta f \cdot t ).$$ | ||
| − | * | + | *Here, the so-called »integral sine function« is used: |
:$${\rm Si}(x) = \int_{ 0 }^{ x } {{\rm si} ( \xi )} \hspace{0.1cm}{\rm d}\xi = x - \frac{x^3}{3 \cdot 3!} + \frac{x^5}{5 \cdot 5!} - \frac{x^7}{7 \cdot 7!}+\text{ ...}$$ | :$${\rm Si}(x) = \int_{ 0 }^{ x } {{\rm si} ( \xi )} \hspace{0.1cm}{\rm d}\xi = x - \frac{x^3}{3 \cdot 3!} + \frac{x^5}{5 \cdot 5!} - \frac{x^7}{7 \cdot 7!}+\text{ ...}$$ | ||
| − | + | :$$\Rightarrow \ {\rm Si}(0) = 0, \hspace{0.3cm}{\rm Si}(\infty) = \frac{\pi}{2}, \hspace{0.3cm}{\rm Si}(-x) = -{\rm Si}(x).$$ | |
| − | :$${\rm Si}(0) = 0, \hspace{0.3cm}{\rm Si}(\infty) = \frac{\pi}{2}, \hspace{0.3cm}{\rm Si}(-x) = -{\rm Si}(x).$$ | + | |
| − | |||
| − | |||
| − | |||
| − | == | + | ==Slit low-pass filter – Rectangular-in-time== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | An LTI system is called a '''»slit low-pass filter«''' $\rm (SLP)$ if the frequency response has the following form: | |
| − | :$$H(f) = {\rm si}(\pi {f}/{ \Delta f})\hspace{0.7cm}{\rm{ | + | :$$H(f) = H_{\rm SLP}(f)= {\rm si}(\pi {f}/{ \Delta f})\hspace{0.7cm}{\rm{where} }\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x},\hspace{0.7cm}{\rm or}$$ |
| − | + | $$\hspace{2.1cm}H_{\rm SLP}(f)= {\rm sinc}({f}/{ \Delta f})\hspace{0.7cm}{\rm{where} }\hspace{0.7cm}{\rm sinc}(x) ={\sin(\pi x)}/{(\pi x)}.$$ | |
| − | + | }} | |
| − | |||
| − | |||
| − | + | [[File:P_ID844__LZI_T_1_3_S3_neu.png |right|frame| Slit low-pass filter: Frequecy response and respective impulse response|class=fit]] | |
| − | + | #From the graph on the left it can be seen that the frequency response $H_{\rm SLP}(f)$ of the slit low-pass filter is identical in shape to the impulse response $h_{\rm RLP}(t)$ of the rectangular low-pass filter. | |
| − | :$$h(t) = \left\{ \begin{array}{l} \hspace{0.25cm}\Delta f \\ \Delta f/2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{ | + | #According to the [[Signal_Representation/Fourier_Transform_Theorems#Duality_Theorem|»Duality Theorem«]] ⇒ the impulse response $h_{\rm SLP}(t)$ of the slit low-pass filter must also have the same form as the frequency response $H_{\rm RLP}(f)$ of the ideal low-pass filter ⇒ "rectangular-in-time". |
| + | #Thus, with the »equivalent duration of the impulse response« $Δt = 1/ Δf$ the following holds: | ||
| + | ::$$h(t) = h_{\rm SLP}(t) = \left\{ \begin{array}{l} \hspace{0.25cm}\Delta f \\ \Delta f/2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert < \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert = \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert > \Delta t/2.} \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | Based on the graph on the right the following statements can be derived: | |
| − | * | + | *The slit low-pass filter in this form is also non-causal. However, adding a transit time of $Δt/2$ or more renders the system causal and thus realizable. |
| − | + | ||
| − | * | + | *The slit low-pass filter acts as an integrator over the time period $Δt$: |
:$$y(t) = x (t) * h (t) = \frac{1}{\Delta t} \cdot \int\limits_{ t - \Delta t/2 }^{ t + \Delta t/2 } {x ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | :$$y(t) = x (t) * h (t) = \frac{1}{\Delta t} \cdot \int\limits_{ t - \Delta t/2 }^{ t + \Delta t/2 } {x ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | * | + | *If $x(t)$ is a harmonic oscillation with frequency $f_0 = k \cdot Δf$ $($where $k$ is an integer$)$, then it integrates exactly over $k$ periods and $y(t) = 0$ holds. |
| + | |||
| + | *This is also shown by the zeros of $H(f)$. | ||
| − | == | + | ==Gaussian low-pass filter == |
<br> | <br> | ||
| − | + | A filter function frequently used for system-theoretical investigations is the Gaussian low-pass filter, which can also be described by only one parameter, namely the [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|»equivalent bandwidth»]] $Δf$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | For the frequency response and the impulse response of the '''»Gaussian low-pass filter«''' $\rm (GLP)$ the following holds: | |
| − | :$$H(f) = {\rm e}^{-\pi(f/\Delta f)^2}\hspace{0.15cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm}h(t) = \Delta f \cdot {\rm e}^{-\pi(\Delta f \cdot \hspace{0.03cm} t)^2} .$$}} | + | :$$H(f) = H_{\rm GLP}(f)= {\rm e}^{-\pi(f/\Delta f)^2}\hspace{0.15cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm}h(t) = h_{\rm GLP}(t) = \Delta f \cdot {\rm e}^{-\pi(\Delta f \cdot \hspace{0.03cm} t)^2} .$$}} |
| − | + | The name goes back to the mathematician, physicist and astronomer [https://en.wikipedia.org/wiki/Carl_Friedrich_Gau%C3%9F $\text{Carl-Friedrich Gauß}$]. Gauß did not deal with this subject matter himself, but the mathematical form of the frequency response and impulse response bear a resemblance to the so-called [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Probability_density_function_.E2.80.93_Cumulative_density_function|»Gaussian formula«]] which he discovered for probability theory. | |
| − | [[File:P_ID845__LZI_T_1_3_S4_neu.png |right|frame| | + | [[File:P_ID845__LZI_T_1_3_S4_neu.png |right|frame| Gaussian low-pass filter: Frequency response and impulse response|class=fit]] |
| − | + | Based on this graph the following statements can be made: | |
| − | + | #The [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|»equivalent pulse duration«]] $Δt$ is also defined via the area-equal rectangle and is equal to the reciprocal of the »equivalent bandwith« $Δf$. | |
| − | + | #A narrow-band $($small $Δf)$ filter function $H(f)$ results in a wide $($large $Δt)$ and simultaneously low impulse response $h(t)$. | |
| − | + | #The so-called [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|»Reciprocity Theorem«]] of time duration and bandwidth can be shown particularly clearly in the example of the Gaussian low-pass filter. | |
| − | + | #The frequency and time domain representations are in principle of the same form. The Gaussian function is also said to be invariant to Fourier transform. | |
| − | + | #The Gaussian low-pass filter is – like the ideal low-pass filter – strongly non-causal and $($exactly$)$ realizable only with infinitely large transit time due to the infinite propagation of its impulse response. | |
| − | + | #However, it must be taken into account that $h(t)$ has already decayed to $1‰$ of its maximum value at $t = 1.5 \cdot Δt$. For $t = 3 \cdot Δt$ we even get $h(t) ≈ 5 · 10^{–13} · h(0)$. | |
| − | + | #These numerical values show that the Gaussian low-pass filter can be used feasibly for practical simulations as long as runtimes do not play a system-limiting role. | |
| − | + | #The »step response« $σ(t)$ is given for the »'''Gaussian error function'''« $ϕ(x)$, which is usually given in tabular form in formula collections: | |
| − | :$$\sigma(t) = \int_{ -\infty }^{ t } {h(\tau)} \hspace{0.1cm}{\rm d}\tau = {\rm \phi}\left( \sqrt{2 \pi }\cdot{t}/{\Delta t} \right) \hspace{0.7cm}{\rm{ | + | ::$$\sigma(t) = \int_{ -\infty }^{ t } {h(\tau)} \hspace{0.1cm}{\rm d}\tau = {\rm \phi}\left( \sqrt{2 \pi }\cdot{t}/{\Delta t} \right) \hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ |
| − | == | + | ==Trapezoidal low-pass filter == |
<br> | <br> | ||
| − | + | The low-pass functions described so far depend on only one parameter – the »equivalent bandwidth« $Δf$. Here, the edge steepness for a given filter type was fixed. Now a low-pass filter with parameterisable edge steepness is described. | |
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The frequency response of the »'''trapezoidal low-pass filter'''« $\rm (TLP)$ with cut-off frequencies $f_1$ and $f_2 \ge f_1$: | |
| − | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 - \vert f \vert }{f_2 -f_1} \\ | + | :$$H(f) = H_{\rm TLP}(f)= \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 - \vert f \vert }{f_2 -f_1} \\ |
\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | ||
| − | \begin{array}{*{10}c} \text{ | + | \begin{array}{*{10}c} \text{for} \\ \text{for} |
| − | \\ \text{ | + | \\ \text{for} \\ \end{array}\begin{array}{*{20}c} |
{\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ | {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ | ||
{f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ | {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ | ||
| Line 121: | Line 133: | ||
| − | + | Instead of $f_1$ and $f_2$ the following parameters can be used to describe $H(f)$: | |
| − | * | + | *the »'''equivalent bandwidth'''« determined via the equal-area rectangle: |
:$$\Delta f = f_1 + f_2.$$ | :$$\Delta f = f_1 + f_2.$$ | ||
| − | * | + | *the »'''roll-off factor'''« $($in frequency domain$)$ as a measure for the edge steepness: |
:$$r_{\hspace{-0.05cm}f} = \frac{f_2 - f_1}{f_2 + f_1}.$$ | :$$r_{\hspace{-0.05cm}f} = \frac{f_2 - f_1}{f_2 + f_1}.$$ | ||
| − | + | Special cases included in the general representation are: | |
| − | * | + | *the ideal rectangular low-pass filter $(r_{\hspace{-0.05cm}f} = 0)$, |
| − | * | + | |
| − | + | *the triangular low-pass filter $(r_{\hspace{-0.05cm}f} = 1)$. | |
| − | |||
| − | |||
| − | |||
| − | + | For a roll-off factor of $r_f = 0.5 \ \Rightarrow \ f_2 = 3f_1$ the following graph shows the frequency response $H(f)= H_{\rm TLP}(f)$ on the left and on the right the impulse response | |
| + | :$$h(t) = h_{\rm TLP}(t) =\Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot {\rm sinc}(r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )\hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm sinc}(x)= \frac{\sin(\pi x)}{\pi x}.$$ | ||
| + | The time-dependent $\rm sinc$–curve of the rectangular low-pass filter with the same equivalent bandwidth is shown dashed for comparison. With the help of the graph and the above equations the following statements can be made: | ||
| − | + | [[File:P_ID846__LZI_T_1_3_S5_neu.png|right |frame| Trapezoidal low-pass filter: Frequency response and impulse response|class=fit]] | |
| − | + | ||
| − | + | #The trapezoidal shape is obtained, for example, by convolution of two rectangles of widths $Δf$ and $r_f \cdot Δf$. | |
| − | + | #According to the convolution theorem the impulse response is thus the product of two $\rm sinc$–functions with arguments $Δf · t$ and $r_{\hspace{-0.05cm}f} · Δf · t$. | |
| − | + | #The first $\rm sinc$–function is part of the $h(t)$ equation for all values of $r_{\hspace{-0.05cm}f}$ and always results in equivalent zero-crossings in the distance $1/Δf$. | |
| − | + | #For $0 \lt r_{\hspace{-0.05cm}f} \lt 1$ there are further zero-crossings at multiples of $Δt/r_{\hspace{-0.05cm}f}$. | |
| − | + | #The larger $r_{\hspace{-0.05cm}f}$ is $($i.e. for a given $Δf$ with a flatter edge$)$, the faster is the asymptotic decay of the impulse response $h(t)$. | |
| − | :$$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm} \frac{{\rm \Delta}f -|f|}{{\rm \Delta}f} \\ | + | #The fastest possible decay is obtained for the triangular low-pass filter ⇒ $r_{\hspace{-0.05cm}f} = 1$, $f_1 = 0$, $f_2 = Δf$. For this, the following holds in frequency and time domains: |
| + | ::$$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm} \frac{{\rm \Delta}f -|f|}{{\rm \Delta}f} \\ | ||
\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | ||
| − | \begin{array}{*{10}c} {\rm{ | + | \begin{array}{*{10}c} {\rm{for}} |
| − | \\ {\rm{ | + | \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} |
{\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ | {\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ | ||
{\hspace{1cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge {\rm \Delta}f } \\ | {\hspace{1cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge {\rm \Delta}f } \\ | ||
| − | \end{array}, | + | \end{array},$$ |
| − | h(t) = \Delta f \cdot {\rm | + | ::$$h(t) = \Delta f \cdot {\rm sinc}^2( \Delta f \cdot t ),\hspace{0.2cm}{\rm{where}}\hspace{0.4cm}{\rm sinc}(x)= \frac{\sin(\pi x)}{\pi x}.$$ |
| − | == | + | ==Raised-cosine low-pass filter == |
<br> | <br> | ||
| − | + | Like the [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Trapezoidal_low-pass_filter|»trapezoidal low-pass filter«]] this low-pass filter is also described by two parameters, which are | |
| − | * | + | *the equivalent bandwidth $Δf$, |
| − | * | + | |
| + | *the roll-off factor $r_{\hspace{-0.05cm}f}$. | ||
| − | + | Its value range lies between $r_{\hspace{-0.05cm}f} = 0$ $($rectangular low-pass filter$)$ and $r_{\hspace{-0.05cm}f} = 1$ $($cosine–squared low-pass filter$)$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | With cut-off frequencies $f_1 = Δf · (1 – r_{\hspace{-0.05cm}f})$ and $f_2 = Δf · (1 + r_{\hspace{-0.05cm}f})$ the frequency response of the »'''raised-cosine low-pass filter'''« $\rm (RCLP)$: | |
| − | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \cos \left( \frac{ \vert f \vert - f_1}{f_2 -f_1}\ | + | :$$H(f) = H_{\rm RCLP}(f) =\left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \cos \left( \frac{ \vert f \vert - f_1}{f_2 -f_1}\cdot \pi/2\right) \\ |
\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | ||
| − | \begin{array}{*{10}c} \text{ | + | \begin{array}{*{10}c} \text{for} \\ \text{for} |
| − | \\ \text{ | + | \\ \text{for} \\ \end{array}\begin{array}{*{20}c} |
{\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ | {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ | ||
{f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ | {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ | ||
| Line 175: | Line 188: | ||
| − | [[File: | + | [[File:EN_LZI_T_1_3_S6_v2.png|frame| Raised-cosine low-pass filter and respective impulse response|class=fit]] |
| − | + | The graph shows $H(f)$ on the left and on the right the impulse response | |
| − | :$$h(t) = \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm | + | :$$h(t) = h_{\rm RCLP}(t) =\Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm sinc}( \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} t )\hspace{-0.05cm}\cdot\hspace{-0.05cm} |
\frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )}{1 - (2 \cdot | \frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )}{1 - (2 \cdot | ||
r_f \cdot \Delta f \cdot t)^2}.$$ | r_f \cdot \Delta f \cdot t)^2}.$$ | ||
| − | + | For these graphs the roll-off factor $r_{\hspace{-0.05cm}f} = 0.5$ was used. In other words: $f_2 = 3 \cdot f_1.$ | |
| − | + | The following is drawn in dashed lines for comparison: | |
| − | * | + | *in the frequency domain the trapezoidal low-pass filter and |
| − | * | + | |
| − | + | *in the time domain the $\rm sinc$ function. | |
| − | |||
| − | |||
| − | |||
| + | $\text{Please note:}$ | ||
| − | + | :The $\rm sinc$–function is not the inverse Fourier transform of the trapezoidal low-pass filter drawn in blue on the left. It rather describes the ideal rectangular low-pass filter in the time domain, which is not shown in the left graph. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Based on this graph and the above equations the following statements can be made: | ||
| + | #The impulse response $h(t)$ of the raised-cosine low-pass filter has zeros at all multiples of $Δt = 1/Δf$, which are due to the $\rm sinc$–function shown in dashed lines in the right-hand figure. | ||
| + | #The last term in the $h(t)$ equation results in further zeros at multiples of $Δt/r_f$. If $1/r_f$ is an integer as in the above graph $(1/r_f = 2)$, these new zeros coincide with the other zeros and thus are not discernible. | ||
| + | #The larger the roll-off factor $r_f$ and thus the flatter the roll-off is, the more favourable is the transient behaviour of the raised-cosine low-pass filter. | ||
| + | #The raised-cosine low-pass filter usually exhibits a better asymptotic transient behaviour than the trapezoidal low-pass filter with same $r_f$ although the latter has a flatter edge at least at frequency $Δf/2$. | ||
| + | #This suggests that the transient behaviour is not only affected by points of discontinuity $($as in the case of the rectangle$)$ but also by kink points as in the case of the trapezoidal low-pass filter. | ||
| + | |||
| + | |||
| + | ==Cosine–square low-pass filter== | ||
| + | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ |
| − | + | For $f_1 = 0$, $f_2 = Δf$ ⇒ $r_f = 1$ the »'''cosine–square low-pass filter'''« $\rm (CSLP)$ is obtained as a special case. Its impulse response can also be represented as follows: | |
| − | :$$ | + | :$$H(f) = H_{\rm CSLP}(f)= \cos^2\Big(\frac{\vert f \vert \hspace{0.05cm}\cdot\hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f}\Big). $$ |
| − | \cdot \ | + | Outside this inner frequency range, $H_{\rm CSLP}(f)=0$.}} |
| − | + | ||
| − | + | ||
| − | + | For the impulse response one obtains according to the inverse Fourier transform after some transformations: | |
| + | :$$h(t)=h_{\rm CSLP}(t)= \Delta f \cdot {\rm sinc}(\Delta f \cdot t)\cdot \big [{\rm sinc}(\Delta f\cdot t +0.5)+{\rm sinc}(\Delta f\cdot t -0.5)\big ],$$ | ||
| + | :$$T=1/\Delta f \hspace{0.5cm}\Rightarrow \hspace{0.5cm} h(t)=1/T \cdot {\rm sinc}(t/T)\cdot \big [{\rm sinc}(t/T +0.5)+{\rm sinc}(t/T -0.5)\big ].$$ | ||
| + | #Because of the first ${\rm sinc}$–function, $h(t)=0$ for multiples of $T=1/\Delta f$ ⇒ the equidistant zero-crossings of the cosine–rolloff lowpass are preserved. | ||
| + | #Because of the bracket expression, $h(t)$ now exhibits further zero-crossings at $t=\pm1.5 T$, $\pm2.5 T$, $\pm3.5 T$, ... but not at $t=\pm0.5 T$. | ||
| + | #For $t=\pm0.5 T$ the impulse response has the value $\Delta f/2$. | ||
| + | #The asymptotic decay of $h(t)$ in this special case runs with $1/t^3$. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Furthermore, it should be mentioned}$ that the »cosine-square low-pass filter« is the only low-pass filter that fulfils both [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_time_domain|'''»Nyquist criteria«]]. Here the »eye« in digital transmission is '''maximally open both vertically and horizontally''' ⇒ see [[Digital_Signal_Transmission/Error_Probability_with_Intersymbol_Interference#Definition_and_statements_of_the_eye_diagram|»Definition and statements of the eye diagram«]].}} | ||
| + | |||
| − | == | + | ==Derivation of system theoretical high-pass functions== |
<br> | <br> | ||
| − | + | So far, six commonly used system theoretic low-pass functions have been considered. For each individual low-pass function there is also an equivalent high-pass function. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | If $H_{\rm TP}(f)$ is a system–theoretical low-pass function $($German "Tiefpass" ⇒ $\text{TP)}$ with $H_{\rm TP}(f = 0) = 1$, then the »'''equivalent high-pass function'''«: | |
:$$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$}} | :$$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$}} | ||
| − | + | Thus, the descriptive quantities in the time domain are: | |
| − | :$$h_{\rm HP}(t) = \delta (t) - h_{\rm TP}(t), | + | :$$h_{\rm HP}(t) = \delta (t) - h_{\rm TP}(t),$$ |
| − | \sigma_{\rm HP}(t) = \gamma (t) - \sigma_{\rm TP}(t). $$ | + | :$$\sigma_{\rm HP}(t) = \gamma (t) - \sigma_{\rm TP}(t). $$ |
| + | |||
| + | Here, the following denotations are used: | ||
| + | #$h_{\rm HP}(t)$ and $h_{\rm TP}(t)$ denote the impulse responses of the high- and low-pass filter, | ||
| + | #$σ_{\rm HP}(t)$ and $σ_{\rm TP}(t)$ denote the respective step responses, | ||
| + | #$γ(t)$ denotes the jump function as a result of integration over the Dirac delta function $δ(t)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | We consider the »slit low-pass filter« ⇒ »rectangular-in-time» which is characterized by | |
| + | [[File: P_ID851__LZI_T_1_3_S7_neu.png |right|frame| Construction of high-pass functions $H_{\rm HP}(f)$, $h_{\rm HP}(t)$, $\sigma_{\rm HP}(t)$ from the <br>corresponding low-pass functions $H_{\rm TP}(f)$, $h_{\rm TP}(t)$, $\sigma_{\rm TP}(t)$|class=fit]] | ||
| + | * a $\rm sinc$–shaped frequency response with $H_{\rm TP}(f = 0) = 1$, | ||
| + | |||
| + | *a rectangular impulse response, and | ||
| + | |||
| + | *a linearly increasing step response. | ||
| + | |||
| + | |||
| + | These are shown in the upper diagram. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | The sketch below shows the corresponding high-pass functions. | |
| − | |||
| − | + | It can be seen that | |
| − | *$H_{\rm HP}(f = 0) | + | *$H_{\rm HP}(f = 0) = 0$ because $H_{\rm TP}(f = 0) = 1$, |
| − | * | + | |
| − | * | + | *consequently the integral over $h_{\rm HP}(t)$ must also be zero, and |
| + | |||
| + | *the step response $σ_{\rm HP}(t)$ tends towards the final value | ||
| + | :$$σ_{\rm HP}(t \to \infty)=0.$$}} | ||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.5:_Rectangular-in-Frequency_Low-Pass_Filter|Exercise 1.5: Rectangular-in-Frequency Low-Pass Filter]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.5Z:_Sinc-shaped_Impulse_Response|Exercise 1.5Z: Sinc-shaped Impulse Response]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.6:_Rectangular-in-Time_Low-Pass_Filter|Exercise 1.6: Rectangular-in-Time Low-Pass Filter]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.6Z:_Interpretation_of_the_Frequency_Response|Exercise 1.6Z: Interpretation of the Frequency Response]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.7:_Nearly_Causal_Gaussian_Low-Pass_Filter|Exercise 1.7: Nearly Causal Gaussian Low-Pass Filter]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.7Z:_Overall_Systems_Analysis|Exercise 1.7Z: Overall Systems Analysis]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.8:_Variable_Edge_Steepness|Exercise 1.8: Variable Edge Steepness]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.8Z:_Cosine-Square_Low-Pass_Filter|Exercise 1.8Z: Cosine-Square Low-Pass Filter]] |
{{Display}} | {{Display}} | ||
Latest revision as of 19:19, 7 November 2023
Contents
- 1 General remarks
- 2 Ideal low-pass filter – Rectangular-in-frequency
- 3 Slit low-pass filter – Rectangular-in-time
- 4 Gaussian low-pass filter
- 5 Trapezoidal low-pass filter
- 6 Raised-cosine low-pass filter
- 7 Cosine–square low-pass filter
- 8 Derivation of system theoretical high-pass functions
- 9 Exercises for the chapter
General remarks
All low-pass functions described in the next sections have the following properties:
- The frequency response $H(f)$ is real and even so that according to the $\text{Assignment Theorem}$ the associated impulse response $h(t)$ is always real and even, too.
- Thus, it is obvious that the systems considered here are non-causal and hence not realizable. The description of causal systems is given in the chapter »Description of Causal Realizable Systems« of this book.
- The advantage of these »system theoretical filter functions« is the simple description by at most two parameters such that the filter influence can be represented in a transparent way.
- The most important frequency response parameter is the »equivalent bandwidth« according to the definition via the equal-area rectangle:
- $$\Delta f = \frac{1}{H(f=0)}\cdot \int_{-\infty}^{+\infty}H(f) \hspace{0.15cm} {\rm d}f.$$
- According to the so-called »Reciprocity Theorem of time duration and bandwidth« the »equivalent duration of the impulse response« is thus fixed, which is also defined via the equal-area rectangle:
- $$\Delta t = \frac{1}{h(t=0)}\cdot \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm} {\rm d}t = \frac{1}{\Delta f}.$$
- The direct signal $\rm (DC)$ transmission factor is always assumed to be $H(f = 0) = 1$ unless explicitly stated otherwise.
- From every low-pass function corresponding high-pass functions can be derived as shown in the section »Derivation of system theoretical high-pass functions«.
Ideal low-pass filter – Rectangular-in-frequency
$\text{Definition:}$ An »ideal low-pass filter« is on hand if its frequency response has the following rectangular shape:
- $$H(f) = H_{\rm RLP}(f) =\left\{ \begin{array}{l} \hspace{0.25cm}1 \\ 0.5 \\\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} \text {for} \\ \text {for} \\ \text {for} \\ \end{array}\begin{array}{*{20}c}{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert< \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert = \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert > \Delta f/2.} \\\end{array}$$
- We sometimes also use the term »rectangular low-pass filter« $\rm (RLP)$.
- Here $Δf$ denotes the »system theoretical bandwidth«.
- $f_{\rm G}=Δf/2$ denotes the »cut-off frequency« $($German: "Grenzfrequenz" ⇒ subscript $\rm G)$.
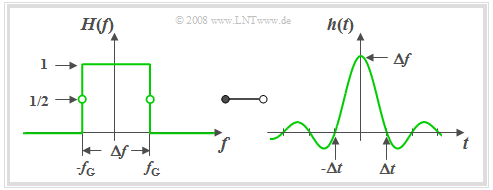
The graph shows such an ideal low-pass filter in the frequency and time domain.
The following can be concluded from these curves:
- Due to the abrupt, infinitely steep roll-off the »3 dB cut-off frequency« ⇒
$f_{\rm G}$ is here exactly half the »system theoretic bandwidth« $Δf$.
- All spectral components with $f \lt f_{\rm G}$ are transmitted undistorted ⇒ »pass band«.
- All components with $f \gt f_{\rm G}$ are completely suppressed ⇒ »stop band«.
- By definition, $H(f) = 0.5$ holds for $f = \pm f_{\rm G}$.
Description of the ideal low-pass filter in the time domain:
- According to the inverse Fourier transform the »impulse response« $($right diagram$)$:
- $$h(t) = h_{\rm RLP}(t) =\Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t)\hspace{0.55cm}{\rm{with}}\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x},\hspace{0.5cm}{\rm or}$$
- $$h_{\rm RLP}(t) =\Delta f \cdot {\rm sinc}(\Delta f \cdot t)\hspace{0.7cm}{\rm{with}}\hspace{0.7cm}{\rm sinc}(x) ={\sin(\pi x)}/{(\pi x)}.$$
- $h(t)$ extended to infinity on both sides and exhibits equidistant zero-crossings at an interval of $Δt = 1/ Δf$.
- The asymptotic decay is inversely proportional to time $|t|$:
- $$|h(t)| = \frac{\Delta f}{\pi \cdot \Delta f \cdot |t|} \cdot \left |{\rm sin}(\pi \cdot \Delta f\cdot t )\right | \le \frac{1}{\pi \cdot |t|}.$$
- It follows that the impulse response is certainly less than $1‰$ of the impulse maximum only for times $t \gt t_{1‰} = 318 \cdot \Delta t$.
- The step response $\sigma(t)$ is obtained from the impulse response by integration and is:
- $${\sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{2} + \frac{1}{\pi} \cdot {\rm Si}(\pi \cdot\Delta f \cdot t ).$$
- Here, the so-called »integral sine function« is used:
- $${\rm Si}(x) = \int_{ 0 }^{ x } {{\rm si} ( \xi )} \hspace{0.1cm}{\rm d}\xi = x - \frac{x^3}{3 \cdot 3!} + \frac{x^5}{5 \cdot 5!} - \frac{x^7}{7 \cdot 7!}+\text{ ...}$$
- $$\Rightarrow \ {\rm Si}(0) = 0, \hspace{0.3cm}{\rm Si}(\infty) = \frac{\pi}{2}, \hspace{0.3cm}{\rm Si}(-x) = -{\rm Si}(x).$$
Slit low-pass filter – Rectangular-in-time
$\text{Definition:}$ An LTI system is called a »slit low-pass filter« $\rm (SLP)$ if the frequency response has the following form:
- $$H(f) = H_{\rm SLP}(f)= {\rm si}(\pi {f}/{ \Delta f})\hspace{0.7cm}{\rm{where} }\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x},\hspace{0.7cm}{\rm or}$$
$$\hspace{2.1cm}H_{\rm SLP}(f)= {\rm sinc}({f}/{ \Delta f})\hspace{0.7cm}{\rm{where} }\hspace{0.7cm}{\rm sinc}(x) ={\sin(\pi x)}/{(\pi x)}.$$
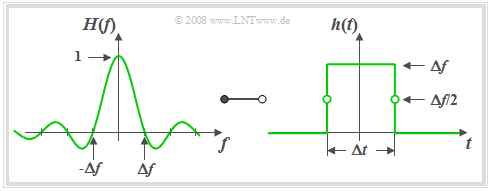
- From the graph on the left it can be seen that the frequency response $H_{\rm SLP}(f)$ of the slit low-pass filter is identical in shape to the impulse response $h_{\rm RLP}(t)$ of the rectangular low-pass filter.
- According to the »Duality Theorem« ⇒ the impulse response $h_{\rm SLP}(t)$ of the slit low-pass filter must also have the same form as the frequency response $H_{\rm RLP}(f)$ of the ideal low-pass filter ⇒ "rectangular-in-time".
- Thus, with the »equivalent duration of the impulse response« $Δt = 1/ Δf$ the following holds:
- $$h(t) = h_{\rm SLP}(t) = \left\{ \begin{array}{l} \hspace{0.25cm}\Delta f \\ \Delta f/2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert < \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert = \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert > \Delta t/2.} \\ \end{array}$$
Based on the graph on the right the following statements can be derived:
- The slit low-pass filter in this form is also non-causal. However, adding a transit time of $Δt/2$ or more renders the system causal and thus realizable.
- The slit low-pass filter acts as an integrator over the time period $Δt$:
- $$y(t) = x (t) * h (t) = \frac{1}{\Delta t} \cdot \int\limits_{ t - \Delta t/2 }^{ t + \Delta t/2 } {x ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$
- If $x(t)$ is a harmonic oscillation with frequency $f_0 = k \cdot Δf$ $($where $k$ is an integer$)$, then it integrates exactly over $k$ periods and $y(t) = 0$ holds.
- This is also shown by the zeros of $H(f)$.
Gaussian low-pass filter
A filter function frequently used for system-theoretical investigations is the Gaussian low-pass filter, which can also be described by only one parameter, namely the »equivalent bandwidth» $Δf$.
$\text{Definition:}$ For the frequency response and the impulse response of the »Gaussian low-pass filter« $\rm (GLP)$ the following holds:
- $$H(f) = H_{\rm GLP}(f)= {\rm e}^{-\pi(f/\Delta f)^2}\hspace{0.15cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm}h(t) = h_{\rm GLP}(t) = \Delta f \cdot {\rm e}^{-\pi(\Delta f \cdot \hspace{0.03cm} t)^2} .$$
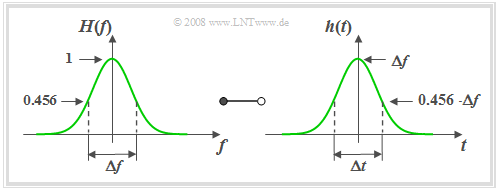
The name goes back to the mathematician, physicist and astronomer $\text{Carl-Friedrich Gauß}$. Gauß did not deal with this subject matter himself, but the mathematical form of the frequency response and impulse response bear a resemblance to the so-called »Gaussian formula« which he discovered for probability theory.
Based on this graph the following statements can be made:
- The »equivalent pulse duration« $Δt$ is also defined via the area-equal rectangle and is equal to the reciprocal of the »equivalent bandwith« $Δf$.
- A narrow-band $($small $Δf)$ filter function $H(f)$ results in a wide $($large $Δt)$ and simultaneously low impulse response $h(t)$.
- The so-called »Reciprocity Theorem« of time duration and bandwidth can be shown particularly clearly in the example of the Gaussian low-pass filter.
- The frequency and time domain representations are in principle of the same form. The Gaussian function is also said to be invariant to Fourier transform.
- The Gaussian low-pass filter is – like the ideal low-pass filter – strongly non-causal and $($exactly$)$ realizable only with infinitely large transit time due to the infinite propagation of its impulse response.
- However, it must be taken into account that $h(t)$ has already decayed to $1‰$ of its maximum value at $t = 1.5 \cdot Δt$. For $t = 3 \cdot Δt$ we even get $h(t) ≈ 5 · 10^{–13} · h(0)$.
- These numerical values show that the Gaussian low-pass filter can be used feasibly for practical simulations as long as runtimes do not play a system-limiting role.
- The »step response« $σ(t)$ is given for the »Gaussian error function« $ϕ(x)$, which is usually given in tabular form in formula collections:
- $$\sigma(t) = \int_{ -\infty }^{ t } {h(\tau)} \hspace{0.1cm}{\rm d}\tau = {\rm \phi}\left( \sqrt{2 \pi }\cdot{t}/{\Delta t} \right) \hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
Trapezoidal low-pass filter
The low-pass functions described so far depend on only one parameter – the »equivalent bandwidth« $Δf$. Here, the edge steepness for a given filter type was fixed. Now a low-pass filter with parameterisable edge steepness is described.
$\text{Definition:}$ The frequency response of the »trapezoidal low-pass filter« $\rm (TLP)$ with cut-off frequencies $f_1$ and $f_2 \ge f_1$:
- $$H(f) = H_{\rm TLP}(f)= \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 - \vert f \vert }{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert > f_2.} \\ \end{array}$$
Instead of $f_1$ and $f_2$ the following parameters can be used to describe $H(f)$:
- the »equivalent bandwidth« determined via the equal-area rectangle:
- $$\Delta f = f_1 + f_2.$$
- the »roll-off factor« $($in frequency domain$)$ as a measure for the edge steepness:
- $$r_{\hspace{-0.05cm}f} = \frac{f_2 - f_1}{f_2 + f_1}.$$
Special cases included in the general representation are:
- the ideal rectangular low-pass filter $(r_{\hspace{-0.05cm}f} = 0)$,
- the triangular low-pass filter $(r_{\hspace{-0.05cm}f} = 1)$.
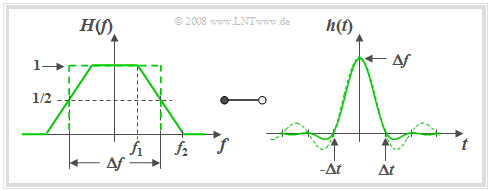
For a roll-off factor of $r_f = 0.5 \ \Rightarrow \ f_2 = 3f_1$ the following graph shows the frequency response $H(f)= H_{\rm TLP}(f)$ on the left and on the right the impulse response
- $$h(t) = h_{\rm TLP}(t) =\Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot {\rm sinc}(r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )\hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm sinc}(x)= \frac{\sin(\pi x)}{\pi x}.$$
The time-dependent $\rm sinc$–curve of the rectangular low-pass filter with the same equivalent bandwidth is shown dashed for comparison. With the help of the graph and the above equations the following statements can be made:
- The trapezoidal shape is obtained, for example, by convolution of two rectangles of widths $Δf$ and $r_f \cdot Δf$.
- According to the convolution theorem the impulse response is thus the product of two $\rm sinc$–functions with arguments $Δf · t$ and $r_{\hspace{-0.05cm}f} · Δf · t$.
- The first $\rm sinc$–function is part of the $h(t)$ equation for all values of $r_{\hspace{-0.05cm}f}$ and always results in equivalent zero-crossings in the distance $1/Δf$.
- For $0 \lt r_{\hspace{-0.05cm}f} \lt 1$ there are further zero-crossings at multiples of $Δt/r_{\hspace{-0.05cm}f}$.
- The larger $r_{\hspace{-0.05cm}f}$ is $($i.e. for a given $Δf$ with a flatter edge$)$, the faster is the asymptotic decay of the impulse response $h(t)$.
- The fastest possible decay is obtained for the triangular low-pass filter ⇒ $r_{\hspace{-0.05cm}f} = 1$, $f_1 = 0$, $f_2 = Δf$. For this, the following holds in frequency and time domains:
- $$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm} \frac{{\rm \Delta}f -|f|}{{\rm \Delta}f} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ {\hspace{1cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge {\rm \Delta}f } \\ \end{array},$$
- $$h(t) = \Delta f \cdot {\rm sinc}^2( \Delta f \cdot t ),\hspace{0.2cm}{\rm{where}}\hspace{0.4cm}{\rm sinc}(x)= \frac{\sin(\pi x)}{\pi x}.$$
Raised-cosine low-pass filter
Like the »trapezoidal low-pass filter« this low-pass filter is also described by two parameters, which are
- the equivalent bandwidth $Δf$,
- the roll-off factor $r_{\hspace{-0.05cm}f}$.
Its value range lies between $r_{\hspace{-0.05cm}f} = 0$ $($rectangular low-pass filter$)$ and $r_{\hspace{-0.05cm}f} = 1$ $($cosine–squared low-pass filter$)$.
$\text{Definition:}$ With cut-off frequencies $f_1 = Δf · (1 – r_{\hspace{-0.05cm}f})$ and $f_2 = Δf · (1 + r_{\hspace{-0.05cm}f})$ the frequency response of the »raised-cosine low-pass filter« $\rm (RCLP)$:
- $$H(f) = H_{\rm RCLP}(f) =\left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \cos \left( \frac{ \vert f \vert - f_1}{f_2 -f_1}\cdot \pi/2\right) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert> f_2.} \\ \end{array}$$
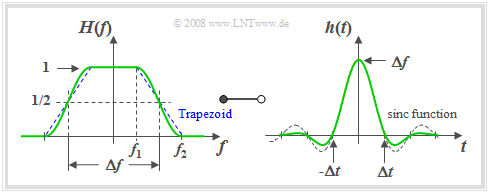
The graph shows $H(f)$ on the left and on the right the impulse response
- $$h(t) = h_{\rm RCLP}(t) =\Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm sinc}( \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} t )\hspace{-0.05cm}\cdot\hspace{-0.05cm} \frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )}{1 - (2 \cdot r_f \cdot \Delta f \cdot t)^2}.$$
For these graphs the roll-off factor $r_{\hspace{-0.05cm}f} = 0.5$ was used. In other words: $f_2 = 3 \cdot f_1.$
The following is drawn in dashed lines for comparison:
- in the frequency domain the trapezoidal low-pass filter and
- in the time domain the $\rm sinc$ function.
$\text{Please note:}$
- The $\rm sinc$–function is not the inverse Fourier transform of the trapezoidal low-pass filter drawn in blue on the left. It rather describes the ideal rectangular low-pass filter in the time domain, which is not shown in the left graph.
Based on this graph and the above equations the following statements can be made:
- The impulse response $h(t)$ of the raised-cosine low-pass filter has zeros at all multiples of $Δt = 1/Δf$, which are due to the $\rm sinc$–function shown in dashed lines in the right-hand figure.
- The last term in the $h(t)$ equation results in further zeros at multiples of $Δt/r_f$. If $1/r_f$ is an integer as in the above graph $(1/r_f = 2)$, these new zeros coincide with the other zeros and thus are not discernible.
- The larger the roll-off factor $r_f$ and thus the flatter the roll-off is, the more favourable is the transient behaviour of the raised-cosine low-pass filter.
- The raised-cosine low-pass filter usually exhibits a better asymptotic transient behaviour than the trapezoidal low-pass filter with same $r_f$ although the latter has a flatter edge at least at frequency $Δf/2$.
- This suggests that the transient behaviour is not only affected by points of discontinuity $($as in the case of the rectangle$)$ but also by kink points as in the case of the trapezoidal low-pass filter.
Cosine–square low-pass filter
$\text{Definition:}$ For $f_1 = 0$, $f_2 = Δf$ ⇒ $r_f = 1$ the »cosine–square low-pass filter« $\rm (CSLP)$ is obtained as a special case. Its impulse response can also be represented as follows:
- $$H(f) = H_{\rm CSLP}(f)= \cos^2\Big(\frac{\vert f \vert \hspace{0.05cm}\cdot\hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f}\Big). $$
Outside this inner frequency range, $H_{\rm CSLP}(f)=0$.
For the impulse response one obtains according to the inverse Fourier transform after some transformations:
- $$h(t)=h_{\rm CSLP}(t)= \Delta f \cdot {\rm sinc}(\Delta f \cdot t)\cdot \big [{\rm sinc}(\Delta f\cdot t +0.5)+{\rm sinc}(\Delta f\cdot t -0.5)\big ],$$
- $$T=1/\Delta f \hspace{0.5cm}\Rightarrow \hspace{0.5cm} h(t)=1/T \cdot {\rm sinc}(t/T)\cdot \big [{\rm sinc}(t/T +0.5)+{\rm sinc}(t/T -0.5)\big ].$$
- Because of the first ${\rm sinc}$–function, $h(t)=0$ for multiples of $T=1/\Delta f$ ⇒ the equidistant zero-crossings of the cosine–rolloff lowpass are preserved.
- Because of the bracket expression, $h(t)$ now exhibits further zero-crossings at $t=\pm1.5 T$, $\pm2.5 T$, $\pm3.5 T$, ... but not at $t=\pm0.5 T$.
- For $t=\pm0.5 T$ the impulse response has the value $\Delta f/2$.
- The asymptotic decay of $h(t)$ in this special case runs with $1/t^3$.
$\text{Furthermore, it should be mentioned}$ that the »cosine-square low-pass filter« is the only low-pass filter that fulfils both »Nyquist criteria«. Here the »eye« in digital transmission is maximally open both vertically and horizontally ⇒ see »Definition and statements of the eye diagram«.
Derivation of system theoretical high-pass functions
So far, six commonly used system theoretic low-pass functions have been considered. For each individual low-pass function there is also an equivalent high-pass function.
$\text{Definition:}$ If $H_{\rm TP}(f)$ is a system–theoretical low-pass function $($German "Tiefpass" ⇒ $\text{TP)}$ with $H_{\rm TP}(f = 0) = 1$, then the »equivalent high-pass function«:
- $$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$
Thus, the descriptive quantities in the time domain are:
- $$h_{\rm HP}(t) = \delta (t) - h_{\rm TP}(t),$$
- $$\sigma_{\rm HP}(t) = \gamma (t) - \sigma_{\rm TP}(t). $$
Here, the following denotations are used:
- $h_{\rm HP}(t)$ and $h_{\rm TP}(t)$ denote the impulse responses of the high- and low-pass filter,
- $σ_{\rm HP}(t)$ and $σ_{\rm TP}(t)$ denote the respective step responses,
- $γ(t)$ denotes the jump function as a result of integration over the Dirac delta function $δ(t)$.
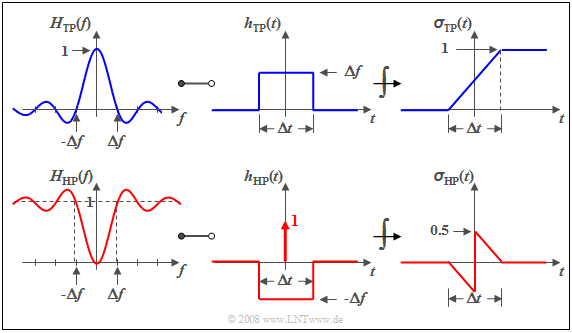
$\text{Example 1:}$ We consider the »slit low-pass filter« ⇒ »rectangular-in-time» which is characterized by
- a $\rm sinc$–shaped frequency response with $H_{\rm TP}(f = 0) = 1$,
- a rectangular impulse response, and
- a linearly increasing step response.
These are shown in the upper diagram.
The sketch below shows the corresponding high-pass functions.
It can be seen that
- $H_{\rm HP}(f = 0) = 0$ because $H_{\rm TP}(f = 0) = 1$,
- consequently the integral over $h_{\rm HP}(t)$ must also be zero, and
- the step response $σ_{\rm HP}(t)$ tends towards the final value
- $$σ_{\rm HP}(t \to \infty)=0.$$
Exercises for the chapter
Exercise 1.5: Rectangular-in-Frequency Low-Pass Filter
Exercise 1.5Z: Sinc-shaped Impulse Response
Exercise 1.6: Rectangular-in-Time Low-Pass Filter
Exercise 1.6Z: Interpretation of the Frequency Response
Exercise 1.7: Nearly Causal Gaussian Low-Pass Filter
Exercise 1.7Z: Overall Systems Analysis
Exercise 1.8: Variable Edge Steepness
Exercise 1.8Z: Cosine-Square Low-Pass Filter