Difference between revisions of "Digital Signal Transmission/Structure of the Optimal Receiver"
| (67 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Generalized Description of Digital Modulation Methods |
|Vorherige Seite=Signale, Basisfunktionen und Vektorräume | |Vorherige Seite=Signale, Basisfunktionen und Vektorräume | ||
|Nächste Seite=Approximation der Fehlerwahrscheinlichkeit | |Nächste Seite=Approximation der Fehlerwahrscheinlichkeit | ||
}} | }} | ||
| − | == | + | == Block diagram and prerequisites == |
<br> | <br> | ||
| − | In | + | In this chapter, the structure of the optimal receiver of a digital transmission system is derived in very general terms, whereby |
| − | * | + | *the modulation process and further system details are not specified further,<br> |
| − | |||
| − | + | *the basis functions and the signal space representation according to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]] are assumed. | |
| − | + | [[File:EN_Dig_T_4_2_S1.png|right|frame|General block diagram of a communication system|class=fit]] | |
| − | + | <br> | |
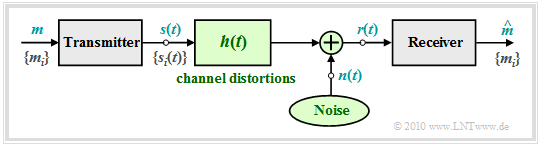
| + | To the block diagram it is to be noted: | ||
| + | *The symbol set size of the source is $M$ and the source symbol set is $\{m_i\}$ with $i = 0$, ... , $M-1$. | ||
| − | * | + | *Let the corresponding source symbol probabilities ${\rm Pr}(m = m_i)$ also be known to the receiver.<br> |
| − | * | + | *For the transmission, $M$ different signal forms $s_i(t)$ are available; for the indexing variable shall be valid: $i = 0$, ... , $M-1$ . |
| − | * | + | *There is a fixed relation between messages $\{m_i\}$ and signals $\{s_i(t)\}$. If $m =m_i$, the transmitted signal is $s(t) =s_i(t)$.<br> |
| − | * | + | *Linear channel distortions are taken into account in the above graph by the impulse response $h(t)$. In addition, the noise term $n(t)$ (of some kind) is effective. |
| − | :: | + | *With these two effects interfering with the transmission, the signal $r(t)$ arriving at the receiver can be given in the following way: |
| + | :$$r(t) = s(t) \star h(t) + n(t) \hspace{0.05cm}.$$ | ||
| − | * | + | *The task of the $($optimal$)$ receiver is to find out on the basis of its input signal $r(t)$, which of the $M$ possible messages $m_i$ – or which of the signals $s_i(t)$ – was sent. The estimated value for $m$ found by the receiver is characterized by a "circumflex" ⇒ $\hat{m}$. |
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| − | : | + | $\text{Definition:}$ One speaks of an '''optimal receiver''' if the symbol error probability assumes the smallest possible value for the boundary conditions: |
| + | :$$p_{\rm S} = {\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm minimum} \hspace{0.05cm}.$$}} | ||
| − | |||
| − | == | + | <u>Notes:</u> |
| + | #In the following, we mostly assume the AWGN approach ⇒ $r(t) = s(t) + n(t)$, which means that $h(t) = \delta(t)$ is assumed to be distortion-free. | ||
| + | #Otherwise, we can redefine the signals $s_i(t)$ as ${s_i}'(t) = s_i(t) \star h(t)$, i.e., impose the deterministic channel distortions on the transmitted signal.<br> | ||
| + | |||
| + | == Fundamental approach to optimal receiver design== | ||
<br> | <br> | ||
| − | + | Compared to the [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#Block_diagram_and_prerequisites|"block diagram"]] shown in the previous section, we now perform some essential generalizations: | |
| − | + | [[File:EN_Dig_T_4_2_S2b.png|right|frame|Model for deriving the optimal receiver|class=fit]] | |
| − | * | + | *The transmission channel is described by the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_Binary_Input|"conditional probability density function"]] $p_{\hspace{0.02cm}r(t)\hspace{0.02cm} \vert \hspace{0.02cm}s(t)}$ which determines the dependence of the received signal $r(t)$ on the transmitted signal $s(t)$. <br> |
| − | : | + | *If a certain signal $r(t) = \rho(t)$ has been received, the receiver has the task to determine the probability density functions based on this "signal realization" $\rho(t)$ and the $M$ conditional probability density functions |
| + | :$$p_{\hspace{0.05cm}r(t) \hspace{0.05cm} \vert \hspace{0.05cm} s(t) } (\rho(t) \hspace{0.05cm} \vert \hspace{0.05cm} s_i(t))\hspace{0.2cm}{\rm with}\hspace{0.2cm} i = 0, \text{...} \hspace{0.05cm}, M-1.$$ | ||
| − | + | *It is to be found out which message $\hat{m}$ was transmitted most probably, taking into account all possible transmitted signals $s_i(t)$ and their occurrence probabilities ${\rm Pr}(m = m_i)$. | |
| − | * | + | *Thus, the estimate of the optimal receiver is determined in general by |
| + | :$$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} p_{\hspace{0.02cm}s(t) \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( s_i(t) \hspace{0.05cm} \vert \hspace{0.05cm} \rho(t)) = {\rm arg} \max_i \hspace{0.1cm} p_{m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( \hspace{0.05cm}m_i\hspace{0.05cm} \vert \hspace{0.05cm}\rho(t))\hspace{0.05cm}.$$ | ||
| − | : | + | {{BlaueBox|TEXT= |
| + | $\text{In other words:}$ The optimal receiver considers as the most likely transmitted message $\hat{m} \in \{m_i\}$ whose conditional probability density function $p_{\hspace{0.02cm}m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) }$ takes the largest possible value for the applied received signal $\rho(t)$ and under the assumption $m =\hat{m}$. }}<br> | ||
| − | : | + | Before we discuss the above decision rule in more detail, the optimal receiver should still be divided into two functional blocks according to the diagram: |
| + | *The '''detector''' takes various measurements on the received signal $r(t)$ and summarizes them in the vector $\boldsymbol{r}$. With $K$ measurements, $\boldsymbol{r}$ corresponds to a point in the $K$–dimensional vector space.<br> | ||
| − | + | *The '''decision''' forms the estimated value depending on this vector. For a given vector $\boldsymbol{r} = \boldsymbol{\rho}$ the decision rule is: | |
| + | :$$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) \hspace{0.05cm}.$$ | ||
| − | + | In contrast to the upper decision rule, a conditional probability $P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} }$ now occurs instead of the conditional probability density function $\rm (PDF)$ $p_{m\hspace{0.05cm} \vert \hspace{0.05cm}r(t)}$. Please note the upper and lower case for the different meanings. | |
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 1:}$ We now consider the function $y = {\rm arg}\hspace{0.05cm} \max \ p(x)$, where $p(x)$ describes the probability density function $\rm (PDF)$ of a continuous-valued or discrete-valued random variable $x$. In the second case (right graph), the PDF consists of a sum of Dirac delta functions with the probabilities as pulse weights.<br> | ||
| − | : | + | [[File:EN_Dig_T_4_2_S2c.png|righ|frame|Illustration of the "arg max" function|class=fit]] |
| − | + | ⇒ The graphic shows exemplary functions. In both cases the PDF maximum $(17)$ is at $x = 6$: | |
| + | :$$\max_i \hspace{0.1cm} p(x) = 17\hspace{0.05cm},$$ | ||
| + | :$$y = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} p(x) = 6\hspace{0.05cm}.$$ | ||
| − | == | + | ⇒ The (conditional) probabilities in the equation |
| − | + | ||
| − | + | :$$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho})$$ | |
| + | |||
| + | are '''a-posteriori probabilities'''. [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Inference_probability|"Bayes' theorem"]] can be used to write for this: | ||
| + | :$$P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) = | ||
| + | \frac{ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )}{p_{\boldsymbol{ r} } (\boldsymbol{\rho})} | ||
| + | \hspace{0.05cm}.$$}} | ||
| + | |||
| + | |||
| + | The denominator term $p_{\boldsymbol{ r} }(\boldsymbol{\rho})$ is the same for all alternatives $m_i$ and need not be considered for the decision. | ||
| + | |||
| + | This gives the following rules: | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Theorem:}$ The decision rule of the optimal receiver, also known as '''maximum–a–posteriori receiver''' $($in short: '''MAP receiver'''$)$ is: | ||
| + | |||
| + | :$$\hat{m}_{\rm MAP} = {\rm \hspace{0.05cm} arg} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}) = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm} m_i )\big ]\hspace{0.05cm}.$$ | ||
| + | |||
| + | *The advantage of this equation is that the conditional PDF $p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m }$ $($"output under the condition input"$)$ describing the forward direction of the channel can be used. | ||
| + | |||
| + | *In contrast, the first equation uses the inference probabilities $P_{\hspace{0.05cm}m\hspace{0.05cm} \vert \hspace{0.02cm} \boldsymbol{ r} } $ $($"input under the condition output"$)$.}} | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Theorem:}$ A '''maximum likelihood receiver''' $($in short: '''ML receiver'''$)$ uses the following decision rule: | ||
| − | + | :$$\hat{m}_{\rm ML} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$ | |
| − | + | *In this case, the possibly different occurrence probabilities ${\rm Pr}(m = m_i)$ are not used for the decision process. | |
| + | *For example, because they are not known to the receiver.}}<br> | ||
| − | + | See the earlier chapter [[Digital_Signal_Transmission/Optimal_Receiver_Strategies|"Optimal Receiver Strategies"]] for other derivations for these receiver types. | |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Conclusion:}$ For equally likely messages $\{m_i\}$ ⇒ ${\rm Pr}(m = m_i) = 1/M$, the generally slightly worse "maximum likelihood receiver" is equivalent to the "maximum–a–posteriori receiver": | ||
| + | :$$\hat{m}_{\rm MAP} = \hat{m}_{\rm ML} =\hspace{-0.1cm} {\rm\hspace{0.05cm} arg} \max_i \hspace{0.1cm} | ||
| + | p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$}} | ||
| − | |||
| − | + | == The irrelevance theorem== | |
| + | <br> | ||
| + | [[File:EN_Dig_T_4_2_S3a.png|right|frame|About the irrelevance theorem|class=fit]] | ||
| + | Note that the receiver described in the last section is optimal only if the detector is implemented in the best possible way, if no information is lost by the transition from the continuous signal $r(t)$ to the vector $\boldsymbol{r}$. <br> | ||
| − | + | To clarify the question which and how many measurements have to be performed on the received signal $r(t)$ to guarantee optimality, the "irrelevance theorem" is helpful. | |
| − | |||
| − | |||
| − | + | *For this purpose, we consider the sketched receiver whose detector derives the two vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$ from the received signal $r(t)$ and makes them available to the decision. | |
| − | { | + | *These quantities are related to the message $ m \in \{m_i\}$ via the composite probability density $p_{\boldsymbol{ r}_1, \hspace{0.05cm}\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}m }$. <br> |
| − | : | + | *The decision rule of the MAP receiver with adaptation to this example is: |
| − | + | :$$\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 , \hspace{0.05cm}\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1, \hspace{0.05cm}\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) \big]= | |
| + | {\rm arg} \max_i \hspace{0.1cm}\big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) | ||
| + | \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )\big] | ||
| + | \hspace{0.05cm}.$$ | ||
| − | {{ | + | Here it is to be noted: |
| + | *The vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$ are random variables. Their realizations are denoted here and in the following by $\boldsymbol{\rho}_1$ and $\boldsymbol{\rho}_2$. For emphasis, all vectors are red inscribed in the graph. | ||
| − | : | + | *The requirements for the application of the "irrelevance theorem" are the same as those for a first order [[Theory_of_Stochastic_Signals/Markov_Chains#Considered_scenario|"Markov chain"]]. The random variables $x$, $y$, $z$ then form a first order Markov chain if the distribution of $z$ is independent of $x$ for a given $y$. The first order Markov chain is the following: |
| + | :$$p(x,\ y,\ z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}y) \hspace{0.75cm} {\rm instead \hspace{0.15cm}of} \hspace{0.75cm}p(x, y, z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}x, y) \hspace{0.05cm}.$$ | ||
| − | + | *In the general case, the optimal receiver must evaluate both vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$, since both composite probability densities $p_{\boldsymbol{ r}_1\hspace{0.05cm} \vert \hspace{0.05cm}m }$ and $p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1, \hspace{0.05cm}m }$ occur in the above decision rule. In contrast, the receiver can neglect the second measurement without loss of information if $\boldsymbol{r}_2$ is independent of the message $m$ for given $\boldsymbol{r}_1$: | |
| + | :$$p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= | ||
| + | p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 ) | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | *In this case, the decision rule can be further simplified: | |
| + | :$$\hat{m}_{\rm MAP} = | ||
| + | {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) | ||
| + | \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) \big]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = | ||
| + | {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) | ||
| + | \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 )\big]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = | ||
| + | {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) | ||
| + | \big]\hspace{0.05cm}.$$ | ||
| − | + | {{GraueBox|TEXT= | |
| − | + | [[File:EN_Dig_T_4_2_S3b.png|right|frame|Two examples of the irrelevance theorem|class=fit]] | |
| + | $\text{Example 2:}$ We consider two different system configurations with two noise terms $\boldsymbol{ n}_1$ and $\boldsymbol{ n}_2$ each to illustrate the irrelevance theorem just presented. | ||
| + | *In the diagram all vectorial quantities are red inscribed. | ||
| + | *Moreover, red inscribed the quantities $\boldsymbol{s}$, $\boldsymbol{ n}_1$ and $\boldsymbol{ n}_2$ are independent of each other.<br> | ||
| − | |||
| − | |||
| − | |||
| − | + | The analysis of these two arrangements yields the following results: | |
| + | *In both cases, the decision must consider the component $\boldsymbol{ r}_1= \boldsymbol{ s}_i + \boldsymbol{ n}_1$, since only this component provides the information about the possible transmitted signals $\boldsymbol{ s}_i$ and thus about the message $m_i$. <br> | ||
| − | + | *In the upper configuration, $\boldsymbol{ r}_2$ contains no information about $m_i$ that has not already been provided by $\boldsymbol{ r}_1$. Rather, $\boldsymbol{ r}_2= \boldsymbol{ r}_1 + \boldsymbol{ n}_2$ is just a noisy version of $\boldsymbol{ r}_1$ and depends only on the noise $\boldsymbol{ n}_2$ once $\boldsymbol{ r}_1$ is known ⇒ $\boldsymbol{ r}_2$ '''is irrelevant''': | |
| + | :$$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= | ||
| + | p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}_1 )= | ||
| + | p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2 - \boldsymbol{\rho}_1 )\hspace{0.05cm}.$$ | ||
| − | + | *In the lower configuration, on the other hand, $\boldsymbol{ r}_2= \boldsymbol{ n}_1 + \boldsymbol{ n}_2$ is helpful to the receiver, since it provides it with an estimate of the noise term $\boldsymbol{ n}_1$ ⇒ $\boldsymbol{ r}_2$ should therefore not be discarded here. | |
| − | : | + | *Formally, this result can be expressed as follows: |
| − | + | :$$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) = p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i)= p_{\boldsymbol{ n}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i) = p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i ) | |
| − | {\ | + | \hspace{0.05cm}.$$ |
| − | |||
| − | \ | ||
| − | \hspace{0.05cm}. | ||
| − | + | *Since the possible transmitted signal $\boldsymbol{ s}_i$ now appears in the argument of this function, $\boldsymbol{ r}_2$ '''is not irrelevant, but quite relevant'''.}}<br> | |
| − | * | ||
| − | |||
| − | + | == Some properties of the AWGN channel== | |
| + | <br> | ||
| + | In order to make further statements about the nature of the optimal measurements of the vector $\boldsymbol{ r}$, it is necessary to further specify the (conditional) probability density function $p_{\hspace{0.02cm}r(t)\hspace{0.05cm} \vert \hspace{0.05cm}s(t)}$ characterizing the channel. In the following, we will consider communication over the [[Modulation_Methods/Quality_Criteria#Some_remarks_on_the_AWGN_channel_model| "AWGN channel"]], whose most important properties are briefly summarized again here: | ||
| + | *The output signal of the AWGN channel is $r(t) = s(t)+n(t)$, where $s(t)$ indicates the transmitted signal and $n(t)$ is represented by a Gaussian noise process.<br> | ||
| − | * | + | *A random process $\{n(t)\}$ is said to be Gaussian if the elements of the $k$–dimensional random variables $\{n_1(t)\hspace{0.05cm} \text{...} \hspace{0.05cm}n_k(t)\}$ are "jointly Gaussian".<br> |
| − | * | + | *The mean value of the AWGN noise is ${\rm E}\big[n(t)\big] = 0$. Moreover, $n(t)$ is "white", which means that the [[Theory_of_Stochastic_Signals/Power-Spectral_Density|"power-spectral density"]] $\rm (PSD)$ is constant for all frequencies $($from $-\infty$ to $+\infty)$: |
| + | :$${\it \Phi}_n(f) = {N_0}/{2} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | :: | + | *According to the [[Theory_of_Stochastic_Signals/Power-Spectral_Density#Wiener-Khintchine_Theorem|"Wiener-Khintchine theorem"]], the auto-correlation function $\rm (ACF)$ is obtained as the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral| "Fourier retransform"]] of ${\it \Phi_n(f)}$: |
| − | + | :$${\varphi_n(\tau)} = {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = {N_0}/{2} \cdot \delta(t)\hspace{0.3cm} | |
| − | \hspace{0.05cm} | + | \Rightarrow \hspace{0.3cm} {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = |
| + | \left\{ \begin{array}{c} \rightarrow \infty \\ | ||
| + | 0 \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm f{or}} \hspace{0.15cm} \tau = 0 \hspace{0.05cm}, | ||
| + | \\ {\rm f{or}} \hspace{0.15cm} \tau \ne 0 \hspace{0.05cm},\\ \end{array}$$ | ||
| − | * | + | *Here, $N_0$ indicates the physical noise power density $($defined only for $f \ge 0)$. The constant PSD value $(N_0/2)$ and the weight of the Dirac delta function in the ACF $($also $N_0/2)$ result from the two-sided approach alone.<br><br> |
| − | + | ⇒ More information on this topic is provided by the (German language) learning video [[Der_AWGN-Kanal_(Lernvideo)|"The AWGN channel"]] in part two.<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ] | ||
| − | |||
| − | == | + | == Description of the AWGN channel by orthonormal basis functions== |
<br> | <br> | ||
| − | + | From the penultimate statement in the last section, we see that | |
| + | *pure AWGN noise $n(t)$ always has infinite variance (power): $\sigma_n^2 \to \infty$,<br> | ||
| − | + | *consequently, in reality only filtered noise $n\hspace{0.05cm}'(t) = n(t) \star h_n(t)$ can occur.<br><br> | |
| − | + | With the impulse response $h_n(t)$ and the frequency response $H_n(f) = {\rm F}\big [h_n(t)\big ]$, the following equations hold:<br> | |
| − | |||
| − | + | :$${\rm E}\big[n\hspace{0.05cm}'(t) \big] \hspace{0.15cm} = \hspace{0.2cm} {\rm E}\big[n(t) \big] = 0 \hspace{0.05cm},$$ | |
| + | :$${\it \Phi_{n\hspace{0.05cm}'}(f)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2} \cdot |H_{n}(f)|^2 \hspace{0.05cm},$$ | ||
| + | :$$ {\it \varphi_{n\hspace{0.05cm}'}(\tau)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2}\hspace{0.1cm} \cdot \big [h_{n}(\tau) \star h_{n}(-\tau)\big ]\hspace{0.05cm},$$ | ||
| + | :$$\sigma_n^2 \hspace{0.1cm} = \hspace{0.1cm} { \varphi_{n\hspace{0.05cm}'}(\tau = 0)} = {N_0}/{2} \cdot | ||
| + | \int_{-\infty}^{+\infty}h_n^2(t)\,{\rm d} t ={N_0}/{2}\hspace{0.1cm} \cdot < \hspace{-0.1cm}h_n(t), \hspace{0.1cm} h_n(t) \hspace{-0.05cm} > \hspace{0.1cm} $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \sigma_n^2 \hspace{0.1cm} = | ||
| + | \int_{-\infty}^{+\infty}{\it \Phi}_{n\hspace{0.05cm}'}(f)\,{\rm d} f = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|H_n(f)|^2\,{\rm d} f \hspace{0.05cm}.$$ | ||
| − | + | In the following, $n(t)$ always implicitly includes a "band limitation"; thus, the notation $n'(t)$ will be omitted in the future.<br> | |
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Please note:}$ Similar to the transmitted signal $s(t)$, the noise process $\{n(t)\}$ can be written as a weighted sum of orthonormal basis functions $\varphi_j(t)$. | ||
| + | *In contrast to $s(t)$, however, a restriction to a finite number of basis functions is not possible. | ||
| − | + | *Rather, for purely stochastic quantities, the following always holds for the corresponding signal representation | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | : | + | :$$n(t) = \lim_{N \rightarrow \infty} \sum\limits_{j = 1}^{N}n_j \cdot \varphi_j(t) \hspace{0.05cm},$$ |
| − | = | + | :where the coefficient $n_j$ is determined by the projection of $n(t)$ onto the basis function $\varphi_j(t)$: |
| + | |||
| + | :$$n_j = \hspace{0.1cm} < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.05cm}.$$}} | ||
| + | |||
| + | |||
| + | <u>Note:</u> To avoid confusion with the basis functions $\varphi_j(t)$, we will in the following express the auto-correlation function $\rm (ACF)$ $\varphi_n(\tau)$ of the noise process only as the expected value | ||
| + | :$${\rm E}\big [n(t) \cdot n(t + \tau)\big ] \equiv \varphi_n(\tau) .$$ <br> | ||
| + | |||
| + | == Optimal receiver for the AWGN channel== | ||
<br> | <br> | ||
| − | + | [[File:EN_Dig_T_4_2_S5b.png|right|frame|Optimal receiver at the AWGN channel|class=fit]] | |
| − | + | The received signal $r(t) = s(t) + n(t)$ can also be decomposed into basis functions in a well-known way: | |
| + | $$r(t) = \sum\limits_{j = 1}^{\infty}r_j \cdot \varphi_j(t) \hspace{0.05cm}.$$ | ||
| − | * | + | To be considered: |
| + | *The $M$ possible transmitted signals $\{s_i(t)\}$ span a signal space with a total of $N$ basis functions $\varphi_1(t)$, ... , $\varphi_N(t)$.<br> | ||
| − | * | + | *These $N$ basis functions $\varphi_j(t)$ are used simultaneously to describe the noise signal $n(t)$ and the received signal $r(t)$. <br> |
| − | + | *For a complete characterization of $n(t)$ or $r(t)$, however, an infinite number of further basis functions $\varphi_{N+1}(t)$, $\varphi_{N+2}(t)$, ... are needed.<br> | |
| − | |||
| − | |||
| − | + | Thus, the coefficients of the received signal $r(t)$ are obtained according to the following equation, taking into account that the signals $s_i(t)$ and the noise $n(t)$ are independent of each other: | |
| − | : | + | :$$r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}=\hspace{0.1cm} |
| − | \left\{ \begin{array}{c} \ | + | \left\{ \begin{array}{c} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > + < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}= s_{ij}+ n_j\\ |
| − | 0 \end{array} \right.\quad | + | < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm} = n_j \end{array} \right.\quad |
| − | \begin{array}{*{1}c} {\ | + | \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm} \hspace{0.05cm}, N} \hspace{0.05cm}, |
| − | + | \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$ | |
| − | + | Thus, the structure sketched above results for the optimal receiver.<br> | |
| + | <br> | ||
| + | Let us first consider the '''AWGN channel'''. Here, the prefilter with the frequency response $W(f)$, which is intended for colored noise, can be dispensed with.<br> | ||
| − | + | #The detector of the optimal receiver forms the coefficients $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t)\hspace{-0.05cm} >$ and passes them on to the decision. | |
| + | #If the decision is based on all $($i.e., infinitely many$)$ coefficients $r_j$, the probability of a wrong decision is minimal and the receiver is optimal.<br> | ||
| + | #The real-valued coefficients $r_j$ were calculated as follows: | ||
| + | ::$$r_j = | ||
| + | \left\{ \begin{array}{c} s_{ij} + n_j\\ | ||
| + | n_j \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, N} \hspace{0.05cm}, | ||
| + | \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$ | ||
| − | + | According to the [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#The_irrelevance_theorem|"irrelevance theorem"]] it can be shown that for additive white Gaussian noise | |
| − | + | *the optimality is not lowered if the coefficients $r_{N+1}$, $r_{N+2}$, ... , that do not depend on the message $(s_{ij})$, are not included in the decision process, and therefore<br> | |
| − | |||
| − | * | ||
| − | |||
| − | + | *the detector has to form only the projections of the received signal $r(t)$ onto the $N$ basis functions $\varphi_{1}(t)$, ... , $\varphi_{N}(t)$ given by the useful signal $s(t)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In the graph this significant simplification is indicated by the gray background.<br> | |
| − | + | In the case of '''colored noise''' ⇒ power-spectral density ${\it \Phi}_n(f) \ne {\rm const.}$, only an additional prefilter with the amplitude response $|W(f)| = {1}/{\sqrt{\it \Phi}_n(f)}$ is required. | |
| + | #This filter is called "whitening filter", because the noise power-spectral density at the output is constant again ⇒ "white". | ||
| + | #More details can be found in the chapter [[Theory_of_Stochastic_Signals/Matched_Filter#Generalized_matched_filter_for_the_case_of_colored_interference|"Matched filter for colored interference"]] of the book "Stochastic Signal Theory".<br> | ||
| − | + | == Implementation aspects == | |
| + | <br> | ||
| + | Essential components of the optimal receiver are the calculations of the inner products according to the equations $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} >$. | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{These can be implemented in several ways:}$ | ||
| + | *In the '''correlation receiver''' $($see the [[Digital_Signal_Transmission/Optimal_Receiver_Strategies#Correlation_receiver_with_unipolar_signaling|"chapter of the same name"]] for more details on this implementation$)$, the inner products are realized directly according to the definition with analog multipliers and integrators: | ||
| + | :$$r_j = \int_{-\infty}^{+\infty}r(t) \cdot \varphi_j(t) \,{\rm d} t \hspace{0.05cm}.$$ | ||
| − | : | + | *The '''matched filter receiver''', already derived in the chapter [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission#Optimal_binary_receiver_.E2.80.93_.22Matched_Filter.22_realization|"Optimal Binary Receiver"]] at the beginning of this book, achieves the same result using a linear filter with impulse response $h_j(t) = \varphi_j(t) \cdot (T-t)$ followed by sampling at time $t = T$: |
| + | :$$r_j = \int_{-\infty}^{+\infty}r(\tau) \cdot h_j(t-\tau) \,{\rm d} \tau | ||
| + | = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(T-t+\tau) \,{\rm d} \tau \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} r_j (t = \tau) = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(\tau) \,{\rm d} \tau = r_j | ||
| + | \hspace{0.05cm}.$$ | ||
| + | [[File:EN_Dig_T_4_2_S6.png|left|frame|Three different implementations of the inner product|class=fit]] | ||
| + | <br><br><br> | ||
| + | The figure shows the two possible realizations <br>of the optimal detector.}} | ||
| − | |||
| − | == | + | == Probability density function of the received values == |
<br> | <br> | ||
| − | + | Before we turn to the optimal design of the decision maker and the calculation and approximation of the error probability in the following chapter, we first perform a statistical analysis of the decision variables $r_j$ valid for the AWGN channel. | |
| − | |||
| − | + | [[File:P ID2009 Dig T 4 2 S7 version1.png|right|frame|Signal space constellation (left) and PDF of the received signal (right)|class=fit]] | |
| − | + | For this purpose, we consider again the optimal binary receiver for bipolar baseband transmission over the AWGN channel, starting from the description form valid for the fourth main chapter. | |
| − | * | + | With the parameters $N = 1$ and $M = 2$, the signal space constellation shown in the left graph is obtained for the transmitted signal |
| + | *with only one basis function $\varphi_1(t)$, because of $N = 1$,<br> | ||
| − | * | + | *with the two signal space points $s_i \in \{s_0, \hspace{0.05cm}s_1\}$, because of $M = 2$. |
| + | <br clear=all> | ||
| + | For the signal $r(t) = s(t) + n(t)$ at the AWGN channel output, the noise-free case ⇒ $r(t) = s(t)$ yields exactly the same constellation; The signal space points are at | ||
| + | :$$r_0 = s_0 = \sqrt{E}\hspace{0.05cm},\hspace{0.2cm}r_1 = s_1 = -\sqrt{E}\hspace{0.05cm}.$$ | ||
| − | + | Considering the (band-limited) AWGN noise $n(t)$, | |
| + | *Gaussian curves with variance $\sigma_n^2$ ⇒ standard deviation $\sigma_n$ are superimposed on each of the two points $r_0$ and $r_1$ $($see right sketch$)$. | ||
| − | + | *The probability density function $\rm (PDF)$ of the noise component $n(t)$ is thereby: | |
| − | : | + | :$$p_n(n) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {n^2}/(2 \sigma_n^2)}\hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The following expression is then obtained for the conditional probability density that the received value $\rho$ is present when $s_i$ has been transmitted: | |
| − | + | :$$p_{\hspace{0.02cm}r\hspace{0.05cm}|\hspace{0.05cm}s}(\rho\hspace{0.05cm}|\hspace{0.05cm}s_i) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {(\rho - s_i)^2}/(2 \sigma_n^2)} \hspace{0.05cm}.$$ | |
| − | + | Regarding the units of the quantities listed here, we note: | |
| + | *$r_0 = s_0$ and $r_1 = s_1$ as well as $n$ are each scalars with the unit "root of energy".<br> | ||
| + | *Thus, it is obvious that $\sigma_n$ also has the unit "root of energy" and $\sigma_n^2$ represents energy.<br> | ||
| + | *For the AWGN channel, the noise variance is $\sigma_n^2 = N_0/2$, so this is also a physical quantity with unit "$\rm W/Hz \equiv Ws$".<br><br> | ||
| + | The topic addressed here is illustrated by examples in [[Aufgaben:Aufgabe_4.06:_Optimale_Entscheidungsgrenzen|"Exercise 4.6"]]. <br> | ||
| + | == N-dimensional Gaussian noise== | ||
| + | <br> | ||
| + | If an $N$–dimensional modulation process is present, i.e., with $0 \le i \le M–1$ and $1 \le j \le N$: | ||
| + | :$$s_i(t) = \sum\limits_{j = 1}^{N} s_{ij} \cdot \varphi_j(t) = s_{i1} \cdot \varphi_1(t) | ||
| + | + s_{i2} \cdot \varphi_2(t) + \hspace{0.05cm}\text{...}\hspace{0.05cm} + s_{iN} \cdot \varphi_N(t)\hspace{0.05cm}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} \boldsymbol{ s}_i = \left(s_{i1}, s_{i2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, s_{iN}\right ) | ||
| + | \hspace{0.05cm},$$ | ||
| + | then the noise vector $\boldsymbol{ n}$ must also be assumed to have dimension $N$. The same is true for the received vector $\boldsymbol{ r}$: | ||
| + | :$$\boldsymbol{ n} = \left(n_{1}, n_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, n_{N}\right ) | ||
| + | \hspace{0.01cm},$$ | ||
| + | :$$\boldsymbol{ r} = \left(r_{1}, r_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, r_{N}\right )\hspace{0.05cm}.$$ | ||
| + | The probability density function $\rm (PDF)$ for the AWGN channel is with the realization $\boldsymbol{ \eta}$ of the noise signal | ||
| + | :$$p_{\boldsymbol{ n}}(\boldsymbol{ \eta}) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^N } \cdot | ||
| + | {\rm exp} \left [ - \frac{|| \boldsymbol{ \eta} ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm},$$ | ||
| + | and for the conditional PDF in the maximum likelihood decision rule: | ||
| + | :$$p_{\hspace{0.02cm}\boldsymbol{ r}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_i) \hspace{-0.1cm} = \hspace{0.1cm} | ||
| + | p_{\hspace{0.02cm} \boldsymbol{ n}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} - \boldsymbol{ s}_i \hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}_i) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot | ||
| + | {\rm exp} \left [ - \frac{|| \boldsymbol{ \rho} - \boldsymbol{ s}_i ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.$$ | ||
| + | The equation follows | ||
| + | *from the general representation of the $N$–dimensional Gaussian PDF in the section [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Correlation_matrix|"correlation matrix"]] of the book "Theory of Stochastic Signals" | ||
| + | |||
| + | *under the assumption that the components are uncorrelated (and thus statistically independent). | ||
| + | *$||\boldsymbol{ \eta}||$ is called the "norm" (length) of the vector $\boldsymbol{ \eta}$.<br> | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 3:}$ | ||
| + | Shown on the right is the two-dimensional Gaussian probability density function $p_{\boldsymbol{ n} } (\boldsymbol{ \eta})$ of the two-dimensional random variable $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$. Arbitrary realizations of the random variable $\boldsymbol{ n}$ are denoted by $\boldsymbol{ \eta} = (\eta_1,\hspace{0.05cm}\eta_2)$. The equation of the represented two-dimensional "Gaussian bell curve" is: | ||
| + | [[File:EN_Dig_T_4_2_S8.png|right|frame|Two-dimensional Gaussian PDF]] | ||
| + | :$$p_{n_1, n_2}(\eta_1, \eta_2) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot | ||
| + | {\rm exp} \left [ - \frac{ \eta_1^2 + \eta_2^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}. $$ | ||
| + | *The maximum of this function is at $\eta_1 = \eta_2 = 0$ and has the value $2\pi \cdot \sigma_n^2$. With $\sigma_n^2 = N_0/2$, the two-dimensional PDF in vector form can also be written as follows: | ||
| + | :$$p_{\boldsymbol{ n} }(\boldsymbol{ \eta}) = \frac{1}{\pi \cdot N_0 } \cdot | ||
| + | {\rm exp} \left [ - \frac{\vert \vert \boldsymbol{ \eta} \vert \vert ^2}{N_0}\right ]\hspace{0.05cm}.$$ | ||
| + | *This rotationally symmetric PDF is suitable e.g. for describing/investigating a "two-dimensional modulation process" such as [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Quadrature_amplitude_modulation_.28M-QAM.29|"M–QAM"]], [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Multi-level_phase.E2.80.93shift_keying_.28M.E2.80.93PSK.29|"M–PSK"]] or [[Modulation_Methods/Non-Linear_Digital_Modulation#FSK_.E2.80.93_Frequency_Shift_Keying|"2–FSK"]].<br> | ||
| + | *However, two-dimensional real random variables are often represented in a one-dimensional complex way, usually in the form $n(t) = n_{\rm I}(t) + {\rm j} \cdot n_{\rm Q}(t)$. The two components are then called the "in-phase component" $n_{\rm I}(t)$ and the "quadrature component" $n_{\rm Q}(t)$ of the noise.<br> | ||
| + | *The probability density function depends only on the magnitude $\vert n(t) \vert$ of the noise variable and not on angle ${\rm arc} \ n(t)$. This means: complex noise is circularly symmetric $($see graph$)$.<br> | ||
| + | *Circularly symmetric also means that the in-phase component $n_{\rm I}(t)$ and the quadrature component $n_{\rm Q}(t)$ have the same distribution and thus also the same variance $($and standard deviation$)$: | ||
| + | :$$ {\rm E} \big [ n_{\rm I}^2(t)\big ] = {\rm E}\big [ n_{\rm Q}^2(t) \big ] = \sigma_n^2 \hspace{0.05cm},\hspace{1cm}{\rm E}\big [ n(t) \cdot n^*(t) \big ]\hspace{0.1cm} = \hspace{0.1cm} {\rm E}\big [ n_{\rm I}^2(t) \big ] + {\rm E}\big [ n_{\rm Q}^2(t)\big ] = 2\sigma_n^2 \hspace{0.05cm}.$$}} | ||
| + | Finally, some '''denotation variants''' for Gaussian random variables: | ||
| + | :$$x ={\cal N}(\mu, \sigma^2) \hspace{-0.1cm}: \hspace{0.3cm}\text{real Gaussian distributed random variable, with mean}\hspace{0.1cm}\mu \text { and variance}\hspace{0.15cm}\sigma^2 \hspace{0.05cm},$$ | ||
| + | :$$y={\cal CN}(\mu, \sigma^2)\hspace{-0.1cm}: \hspace{0.12cm}\text{complex Gaussian distributed random variable} \hspace{0.05cm}.$$ | ||
| + | == Exercises for the chapter== | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_4.4:_Maximum–a–posteriori_and_Maximum–Likelihood|Exercise 4.4: Maximum–a–posteriori and Maximum–Likelihood]] | ||
| + | [[Aufgaben:Exercise_4.5:_Irrelevance_Theorem|Exercise 4.5: Irrelevance Theorem]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 15:18, 23 January 2023
Contents
- 1 Block diagram and prerequisites
- 2 Fundamental approach to optimal receiver design
- 3 The irrelevance theorem
- 4 Some properties of the AWGN channel
- 5 Description of the AWGN channel by orthonormal basis functions
- 6 Optimal receiver for the AWGN channel
- 7 Implementation aspects
- 8 Probability density function of the received values
- 9 N-dimensional Gaussian noise
- 10 Exercises for the chapter
Block diagram and prerequisites
In this chapter, the structure of the optimal receiver of a digital transmission system is derived in very general terms, whereby
- the modulation process and further system details are not specified further,
- the basis functions and the signal space representation according to the chapter "Signals, Basis Functions and Vector Spaces" are assumed.
To the block diagram it is to be noted:
- The symbol set size of the source is $M$ and the source symbol set is $\{m_i\}$ with $i = 0$, ... , $M-1$.
- Let the corresponding source symbol probabilities ${\rm Pr}(m = m_i)$ also be known to the receiver.
- For the transmission, $M$ different signal forms $s_i(t)$ are available; for the indexing variable shall be valid: $i = 0$, ... , $M-1$ .
- There is a fixed relation between messages $\{m_i\}$ and signals $\{s_i(t)\}$. If $m =m_i$, the transmitted signal is $s(t) =s_i(t)$.
- Linear channel distortions are taken into account in the above graph by the impulse response $h(t)$. In addition, the noise term $n(t)$ (of some kind) is effective.
- With these two effects interfering with the transmission, the signal $r(t)$ arriving at the receiver can be given in the following way:
- $$r(t) = s(t) \star h(t) + n(t) \hspace{0.05cm}.$$
- The task of the $($optimal$)$ receiver is to find out on the basis of its input signal $r(t)$, which of the $M$ possible messages $m_i$ – or which of the signals $s_i(t)$ – was sent. The estimated value for $m$ found by the receiver is characterized by a "circumflex" ⇒ $\hat{m}$.
$\text{Definition:}$ One speaks of an optimal receiver if the symbol error probability assumes the smallest possible value for the boundary conditions:
- $$p_{\rm S} = {\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm minimum} \hspace{0.05cm}.$$
Notes:
- In the following, we mostly assume the AWGN approach ⇒ $r(t) = s(t) + n(t)$, which means that $h(t) = \delta(t)$ is assumed to be distortion-free.
- Otherwise, we can redefine the signals $s_i(t)$ as ${s_i}'(t) = s_i(t) \star h(t)$, i.e., impose the deterministic channel distortions on the transmitted signal.
Fundamental approach to optimal receiver design
Compared to the "block diagram" shown in the previous section, we now perform some essential generalizations:
- The transmission channel is described by the "conditional probability density function" $p_{\hspace{0.02cm}r(t)\hspace{0.02cm} \vert \hspace{0.02cm}s(t)}$ which determines the dependence of the received signal $r(t)$ on the transmitted signal $s(t)$.
- If a certain signal $r(t) = \rho(t)$ has been received, the receiver has the task to determine the probability density functions based on this "signal realization" $\rho(t)$ and the $M$ conditional probability density functions
- $$p_{\hspace{0.05cm}r(t) \hspace{0.05cm} \vert \hspace{0.05cm} s(t) } (\rho(t) \hspace{0.05cm} \vert \hspace{0.05cm} s_i(t))\hspace{0.2cm}{\rm with}\hspace{0.2cm} i = 0, \text{...} \hspace{0.05cm}, M-1.$$
- It is to be found out which message $\hat{m}$ was transmitted most probably, taking into account all possible transmitted signals $s_i(t)$ and their occurrence probabilities ${\rm Pr}(m = m_i)$.
- Thus, the estimate of the optimal receiver is determined in general by
- $$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} p_{\hspace{0.02cm}s(t) \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( s_i(t) \hspace{0.05cm} \vert \hspace{0.05cm} \rho(t)) = {\rm arg} \max_i \hspace{0.1cm} p_{m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) } ( \hspace{0.05cm}m_i\hspace{0.05cm} \vert \hspace{0.05cm}\rho(t))\hspace{0.05cm}.$$
$\text{In other words:}$ The optimal receiver considers as the most likely transmitted message $\hat{m} \in \{m_i\}$ whose conditional probability density function $p_{\hspace{0.02cm}m \hspace{0.05cm} \vert \hspace{0.05cm} r(t) }$ takes the largest possible value for the applied received signal $\rho(t)$ and under the assumption $m =\hat{m}$.
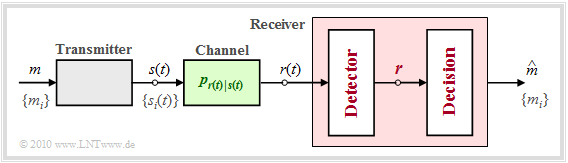
Before we discuss the above decision rule in more detail, the optimal receiver should still be divided into two functional blocks according to the diagram:
- The detector takes various measurements on the received signal $r(t)$ and summarizes them in the vector $\boldsymbol{r}$. With $K$ measurements, $\boldsymbol{r}$ corresponds to a point in the $K$–dimensional vector space.
- The decision forms the estimated value depending on this vector. For a given vector $\boldsymbol{r} = \boldsymbol{\rho}$ the decision rule is:
- $$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) \hspace{0.05cm}.$$
In contrast to the upper decision rule, a conditional probability $P_{m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} }$ now occurs instead of the conditional probability density function $\rm (PDF)$ $p_{m\hspace{0.05cm} \vert \hspace{0.05cm}r(t)}$. Please note the upper and lower case for the different meanings.
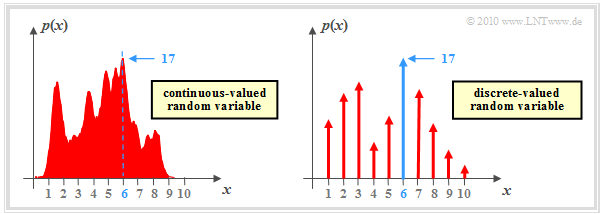
$\text{Example 1:}$ We now consider the function $y = {\rm arg}\hspace{0.05cm} \max \ p(x)$, where $p(x)$ describes the probability density function $\rm (PDF)$ of a continuous-valued or discrete-valued random variable $x$. In the second case (right graph), the PDF consists of a sum of Dirac delta functions with the probabilities as pulse weights.
⇒ The graphic shows exemplary functions. In both cases the PDF maximum $(17)$ is at $x = 6$:
- $$\max_i \hspace{0.1cm} p(x) = 17\hspace{0.05cm},$$
- $$y = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} p(x) = 6\hspace{0.05cm}.$$
⇒ The (conditional) probabilities in the equation
- $$\hat{m} = {\rm arg}\hspace{0.05cm} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho})$$
are a-posteriori probabilities. "Bayes' theorem" can be used to write for this:
- $$P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}) = \frac{ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )}{p_{\boldsymbol{ r} } (\boldsymbol{\rho})} \hspace{0.05cm}.$$
The denominator term $p_{\boldsymbol{ r} }(\boldsymbol{\rho})$ is the same for all alternatives $m_i$ and need not be considered for the decision.
This gives the following rules:
$\text{Theorem:}$ The decision rule of the optimal receiver, also known as maximum–a–posteriori receiver $($in short: MAP receiver$)$ is:
- $$\hat{m}_{\rm MAP} = {\rm \hspace{0.05cm} arg} \max_i \hspace{0.1cm} P_{\hspace{0.02cm}m\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r} } ( m_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}) = {\rm \hspace{0.05cm}arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm} m_i )\big ]\hspace{0.05cm}.$$
- The advantage of this equation is that the conditional PDF $p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm} m }$ $($"output under the condition input"$)$ describing the forward direction of the channel can be used.
- In contrast, the first equation uses the inference probabilities $P_{\hspace{0.05cm}m\hspace{0.05cm} \vert \hspace{0.02cm} \boldsymbol{ r} } $ $($"input under the condition output"$)$.
$\text{Theorem:}$ A maximum likelihood receiver $($in short: ML receiver$)$ uses the following decision rule:
- $$\hat{m}_{\rm ML} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$
- In this case, the possibly different occurrence probabilities ${\rm Pr}(m = m_i)$ are not used for the decision process.
- For example, because they are not known to the receiver.
See the earlier chapter "Optimal Receiver Strategies" for other derivations for these receiver types.
$\text{Conclusion:}$ For equally likely messages $\{m_i\}$ ⇒ ${\rm Pr}(m = m_i) = 1/M$, the generally slightly worse "maximum likelihood receiver" is equivalent to the "maximum–a–posteriori receiver":
- $$\hat{m}_{\rm MAP} = \hat{m}_{\rm ML} =\hspace{-0.1cm} {\rm\hspace{0.05cm} arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}\hspace{0.05cm} \vert \hspace{0.05cm}m } (\boldsymbol{\rho}\hspace{0.05cm} \vert \hspace{0.05cm}m_i )\hspace{0.05cm}.$$
The irrelevance theorem
Note that the receiver described in the last section is optimal only if the detector is implemented in the best possible way, if no information is lost by the transition from the continuous signal $r(t)$ to the vector $\boldsymbol{r}$.
To clarify the question which and how many measurements have to be performed on the received signal $r(t)$ to guarantee optimality, the "irrelevance theorem" is helpful.
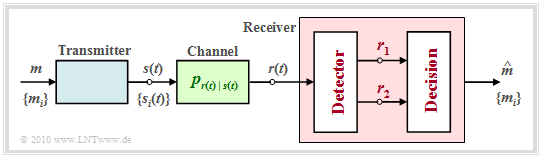
- For this purpose, we consider the sketched receiver whose detector derives the two vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$ from the received signal $r(t)$ and makes them available to the decision.
- These quantities are related to the message $ m \in \{m_i\}$ via the composite probability density $p_{\boldsymbol{ r}_1, \hspace{0.05cm}\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}m }$.
- The decision rule of the MAP receiver with adaptation to this example is:
- $$\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 , \hspace{0.05cm}\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1, \hspace{0.05cm}\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) \big]= {\rm arg} \max_i \hspace{0.1cm}\big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )\big] \hspace{0.05cm}.$$
Here it is to be noted:
- The vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$ are random variables. Their realizations are denoted here and in the following by $\boldsymbol{\rho}_1$ and $\boldsymbol{\rho}_2$. For emphasis, all vectors are red inscribed in the graph.
- The requirements for the application of the "irrelevance theorem" are the same as those for a first order "Markov chain". The random variables $x$, $y$, $z$ then form a first order Markov chain if the distribution of $z$ is independent of $x$ for a given $y$. The first order Markov chain is the following:
- $$p(x,\ y,\ z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}y) \hspace{0.75cm} {\rm instead \hspace{0.15cm}of} \hspace{0.75cm}p(x, y, z) = p(x) \cdot p(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot p(z\hspace{0.05cm} \vert \hspace{0.05cm}x, y) \hspace{0.05cm}.$$
- In the general case, the optimal receiver must evaluate both vectors $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$, since both composite probability densities $p_{\boldsymbol{ r}_1\hspace{0.05cm} \vert \hspace{0.05cm}m }$ and $p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1, \hspace{0.05cm}m }$ occur in the above decision rule. In contrast, the receiver can neglect the second measurement without loss of information if $\boldsymbol{r}_2$ is independent of the message $m$ for given $\boldsymbol{r}_1$:
- $$p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 ) \hspace{0.05cm}.$$
- In this case, the decision rule can be further simplified:
- $$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) \big]$$
- $$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \cdot p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 )\big]$$
- $$\Rightarrow \hspace{0.3cm}\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m } \hspace{0.05cm} (\boldsymbol{\rho}_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_i ) \big]\hspace{0.05cm}.$$
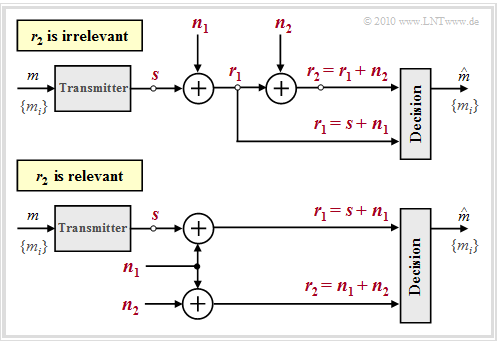
$\text{Example 2:}$ We consider two different system configurations with two noise terms $\boldsymbol{ n}_1$ and $\boldsymbol{ n}_2$ each to illustrate the irrelevance theorem just presented.
- In the diagram all vectorial quantities are red inscribed.
- Moreover, red inscribed the quantities $\boldsymbol{s}$, $\boldsymbol{ n}_1$ and $\boldsymbol{ n}_2$ are independent of each other.
The analysis of these two arrangements yields the following results:
- In both cases, the decision must consider the component $\boldsymbol{ r}_1= \boldsymbol{ s}_i + \boldsymbol{ n}_1$, since only this component provides the information about the possible transmitted signals $\boldsymbol{ s}_i$ and thus about the message $m_i$.
- In the upper configuration, $\boldsymbol{ r}_2$ contains no information about $m_i$ that has not already been provided by $\boldsymbol{ r}_1$. Rather, $\boldsymbol{ r}_2= \boldsymbol{ r}_1 + \boldsymbol{ n}_2$ is just a noisy version of $\boldsymbol{ r}_1$ and depends only on the noise $\boldsymbol{ n}_2$ once $\boldsymbol{ r}_1$ is known ⇒ $\boldsymbol{ r}_2$ is irrelevant:
- $$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm}\boldsymbol{\rho}_1 )= p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2 - \boldsymbol{\rho}_1 )\hspace{0.05cm}.$$
- In the lower configuration, on the other hand, $\boldsymbol{ r}_2= \boldsymbol{ n}_1 + \boldsymbol{ n}_2$ is helpful to the receiver, since it provides it with an estimate of the noise term $\boldsymbol{ n}_1$ ⇒ $\boldsymbol{ r}_2$ should therefore not be discarded here.
- Formally, this result can be expressed as follows:
- $$p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2\hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) = p_{\boldsymbol{ r}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i)= p_{\boldsymbol{ n}_2 \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i \hspace{0.05cm} \vert \hspace{0.05cm} \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i) = p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i ) \hspace{0.05cm}.$$
- Since the possible transmitted signal $\boldsymbol{ s}_i$ now appears in the argument of this function, $\boldsymbol{ r}_2$ is not irrelevant, but quite relevant.
Some properties of the AWGN channel
In order to make further statements about the nature of the optimal measurements of the vector $\boldsymbol{ r}$, it is necessary to further specify the (conditional) probability density function $p_{\hspace{0.02cm}r(t)\hspace{0.05cm} \vert \hspace{0.05cm}s(t)}$ characterizing the channel. In the following, we will consider communication over the "AWGN channel", whose most important properties are briefly summarized again here:
- The output signal of the AWGN channel is $r(t) = s(t)+n(t)$, where $s(t)$ indicates the transmitted signal and $n(t)$ is represented by a Gaussian noise process.
- A random process $\{n(t)\}$ is said to be Gaussian if the elements of the $k$–dimensional random variables $\{n_1(t)\hspace{0.05cm} \text{...} \hspace{0.05cm}n_k(t)\}$ are "jointly Gaussian".
- The mean value of the AWGN noise is ${\rm E}\big[n(t)\big] = 0$. Moreover, $n(t)$ is "white", which means that the "power-spectral density" $\rm (PSD)$ is constant for all frequencies $($from $-\infty$ to $+\infty)$:
- $${\it \Phi}_n(f) = {N_0}/{2} \hspace{0.05cm}.$$
- According to the "Wiener-Khintchine theorem", the auto-correlation function $\rm (ACF)$ is obtained as the "Fourier retransform" of ${\it \Phi_n(f)}$:
- $${\varphi_n(\tau)} = {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = {N_0}/{2} \cdot \delta(t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm E}\big [n(t) \cdot n(t+\tau)\big ] = \left\{ \begin{array}{c} \rightarrow \infty \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{or}} \hspace{0.15cm} \tau = 0 \hspace{0.05cm}, \\ {\rm f{or}} \hspace{0.15cm} \tau \ne 0 \hspace{0.05cm},\\ \end{array}$$
- Here, $N_0$ indicates the physical noise power density $($defined only for $f \ge 0)$. The constant PSD value $(N_0/2)$ and the weight of the Dirac delta function in the ACF $($also $N_0/2)$ result from the two-sided approach alone.
⇒ More information on this topic is provided by the (German language) learning video "The AWGN channel" in part two.
Description of the AWGN channel by orthonormal basis functions
From the penultimate statement in the last section, we see that
- pure AWGN noise $n(t)$ always has infinite variance (power): $\sigma_n^2 \to \infty$,
- consequently, in reality only filtered noise $n\hspace{0.05cm}'(t) = n(t) \star h_n(t)$ can occur.
With the impulse response $h_n(t)$ and the frequency response $H_n(f) = {\rm F}\big [h_n(t)\big ]$, the following equations hold:
- $${\rm E}\big[n\hspace{0.05cm}'(t) \big] \hspace{0.15cm} = \hspace{0.2cm} {\rm E}\big[n(t) \big] = 0 \hspace{0.05cm},$$
- $${\it \Phi_{n\hspace{0.05cm}'}(f)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2} \cdot |H_{n}(f)|^2 \hspace{0.05cm},$$
- $$ {\it \varphi_{n\hspace{0.05cm}'}(\tau)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2}\hspace{0.1cm} \cdot \big [h_{n}(\tau) \star h_{n}(-\tau)\big ]\hspace{0.05cm},$$
- $$\sigma_n^2 \hspace{0.1cm} = \hspace{0.1cm} { \varphi_{n\hspace{0.05cm}'}(\tau = 0)} = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}h_n^2(t)\,{\rm d} t ={N_0}/{2}\hspace{0.1cm} \cdot < \hspace{-0.1cm}h_n(t), \hspace{0.1cm} h_n(t) \hspace{-0.05cm} > \hspace{0.1cm} $$
- $$\Rightarrow \hspace{0.3cm} \sigma_n^2 \hspace{0.1cm} = \int_{-\infty}^{+\infty}{\it \Phi}_{n\hspace{0.05cm}'}(f)\,{\rm d} f = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|H_n(f)|^2\,{\rm d} f \hspace{0.05cm}.$$
In the following, $n(t)$ always implicitly includes a "band limitation"; thus, the notation $n'(t)$ will be omitted in the future.
$\text{Please note:}$ Similar to the transmitted signal $s(t)$, the noise process $\{n(t)\}$ can be written as a weighted sum of orthonormal basis functions $\varphi_j(t)$.
- In contrast to $s(t)$, however, a restriction to a finite number of basis functions is not possible.
- Rather, for purely stochastic quantities, the following always holds for the corresponding signal representation
- $$n(t) = \lim_{N \rightarrow \infty} \sum\limits_{j = 1}^{N}n_j \cdot \varphi_j(t) \hspace{0.05cm},$$
- where the coefficient $n_j$ is determined by the projection of $n(t)$ onto the basis function $\varphi_j(t)$:
- $$n_j = \hspace{0.1cm} < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.05cm}.$$
Note: To avoid confusion with the basis functions $\varphi_j(t)$, we will in the following express the auto-correlation function $\rm (ACF)$ $\varphi_n(\tau)$ of the noise process only as the expected value
- $${\rm E}\big [n(t) \cdot n(t + \tau)\big ] \equiv \varphi_n(\tau) .$$
Optimal receiver for the AWGN channel
The received signal $r(t) = s(t) + n(t)$ can also be decomposed into basis functions in a well-known way: $$r(t) = \sum\limits_{j = 1}^{\infty}r_j \cdot \varphi_j(t) \hspace{0.05cm}.$$
To be considered:
- The $M$ possible transmitted signals $\{s_i(t)\}$ span a signal space with a total of $N$ basis functions $\varphi_1(t)$, ... , $\varphi_N(t)$.
- These $N$ basis functions $\varphi_j(t)$ are used simultaneously to describe the noise signal $n(t)$ and the received signal $r(t)$.
- For a complete characterization of $n(t)$ or $r(t)$, however, an infinite number of further basis functions $\varphi_{N+1}(t)$, $\varphi_{N+2}(t)$, ... are needed.
Thus, the coefficients of the received signal $r(t)$ are obtained according to the following equation, taking into account that the signals $s_i(t)$ and the noise $n(t)$ are independent of each other:
- $$r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}=\hspace{0.1cm} \left\{ \begin{array}{c} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > + < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}= s_{ij}+ n_j\\ < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm} = n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm} \hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$
Thus, the structure sketched above results for the optimal receiver.
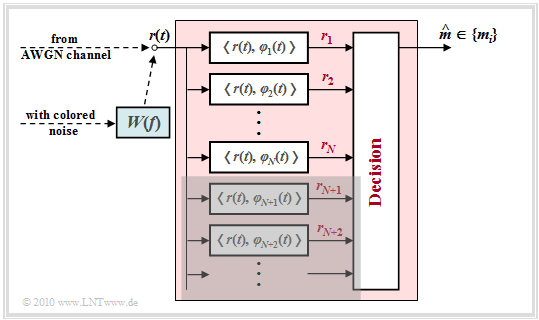
Let us first consider the AWGN channel. Here, the prefilter with the frequency response $W(f)$, which is intended for colored noise, can be dispensed with.
- The detector of the optimal receiver forms the coefficients $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t)\hspace{-0.05cm} >$ and passes them on to the decision.
- If the decision is based on all $($i.e., infinitely many$)$ coefficients $r_j$, the probability of a wrong decision is minimal and the receiver is optimal.
- The real-valued coefficients $r_j$ were calculated as follows:
- $$r_j = \left\{ \begin{array}{c} s_{ij} + n_j\\ n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}$$
According to the "irrelevance theorem" it can be shown that for additive white Gaussian noise
- the optimality is not lowered if the coefficients $r_{N+1}$, $r_{N+2}$, ... , that do not depend on the message $(s_{ij})$, are not included in the decision process, and therefore
- the detector has to form only the projections of the received signal $r(t)$ onto the $N$ basis functions $\varphi_{1}(t)$, ... , $\varphi_{N}(t)$ given by the useful signal $s(t)$.
In the graph this significant simplification is indicated by the gray background.
In the case of colored noise ⇒ power-spectral density ${\it \Phi}_n(f) \ne {\rm const.}$, only an additional prefilter with the amplitude response $|W(f)| = {1}/{\sqrt{\it \Phi}_n(f)}$ is required.
- This filter is called "whitening filter", because the noise power-spectral density at the output is constant again ⇒ "white".
- More details can be found in the chapter "Matched filter for colored interference" of the book "Stochastic Signal Theory".
Implementation aspects
Essential components of the optimal receiver are the calculations of the inner products according to the equations $r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} >$.
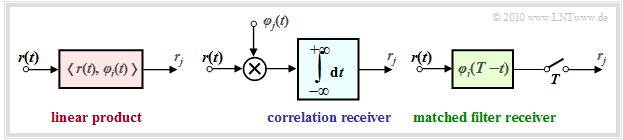
$\text{These can be implemented in several ways:}$
- In the correlation receiver $($see the "chapter of the same name" for more details on this implementation$)$, the inner products are realized directly according to the definition with analog multipliers and integrators:
- $$r_j = \int_{-\infty}^{+\infty}r(t) \cdot \varphi_j(t) \,{\rm d} t \hspace{0.05cm}.$$
- The matched filter receiver, already derived in the chapter "Optimal Binary Receiver" at the beginning of this book, achieves the same result using a linear filter with impulse response $h_j(t) = \varphi_j(t) \cdot (T-t)$ followed by sampling at time $t = T$:
- $$r_j = \int_{-\infty}^{+\infty}r(\tau) \cdot h_j(t-\tau) \,{\rm d} \tau = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(T-t+\tau) \,{\rm d} \tau \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_j (t = \tau) = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(\tau) \,{\rm d} \tau = r_j \hspace{0.05cm}.$$
The figure shows the two possible realizations
of the optimal detector.
Probability density function of the received values
Before we turn to the optimal design of the decision maker and the calculation and approximation of the error probability in the following chapter, we first perform a statistical analysis of the decision variables $r_j$ valid for the AWGN channel.
For this purpose, we consider again the optimal binary receiver for bipolar baseband transmission over the AWGN channel, starting from the description form valid for the fourth main chapter.
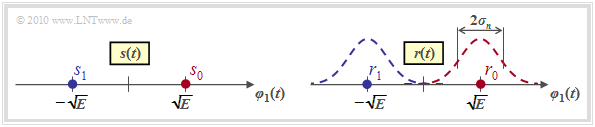
With the parameters $N = 1$ and $M = 2$, the signal space constellation shown in the left graph is obtained for the transmitted signal
- with only one basis function $\varphi_1(t)$, because of $N = 1$,
- with the two signal space points $s_i \in \{s_0, \hspace{0.05cm}s_1\}$, because of $M = 2$.
For the signal $r(t) = s(t) + n(t)$ at the AWGN channel output, the noise-free case ⇒ $r(t) = s(t)$ yields exactly the same constellation; The signal space points are at
- $$r_0 = s_0 = \sqrt{E}\hspace{0.05cm},\hspace{0.2cm}r_1 = s_1 = -\sqrt{E}\hspace{0.05cm}.$$
Considering the (band-limited) AWGN noise $n(t)$,
- Gaussian curves with variance $\sigma_n^2$ ⇒ standard deviation $\sigma_n$ are superimposed on each of the two points $r_0$ and $r_1$ $($see right sketch$)$.
- The probability density function $\rm (PDF)$ of the noise component $n(t)$ is thereby:
- $$p_n(n) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {n^2}/(2 \sigma_n^2)}\hspace{0.05cm}.$$
The following expression is then obtained for the conditional probability density that the received value $\rho$ is present when $s_i$ has been transmitted:
- $$p_{\hspace{0.02cm}r\hspace{0.05cm}|\hspace{0.05cm}s}(\rho\hspace{0.05cm}|\hspace{0.05cm}s_i) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm e}^{ - {(\rho - s_i)^2}/(2 \sigma_n^2)} \hspace{0.05cm}.$$
Regarding the units of the quantities listed here, we note:
- $r_0 = s_0$ and $r_1 = s_1$ as well as $n$ are each scalars with the unit "root of energy".
- Thus, it is obvious that $\sigma_n$ also has the unit "root of energy" and $\sigma_n^2$ represents energy.
- For the AWGN channel, the noise variance is $\sigma_n^2 = N_0/2$, so this is also a physical quantity with unit "$\rm W/Hz \equiv Ws$".
The topic addressed here is illustrated by examples in "Exercise 4.6".
N-dimensional Gaussian noise
If an $N$–dimensional modulation process is present, i.e., with $0 \le i \le M–1$ and $1 \le j \le N$:
- $$s_i(t) = \sum\limits_{j = 1}^{N} s_{ij} \cdot \varphi_j(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + \hspace{0.05cm}\text{...}\hspace{0.05cm} + s_{iN} \cdot \varphi_N(t)\hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \boldsymbol{ s}_i = \left(s_{i1}, s_{i2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, s_{iN}\right ) \hspace{0.05cm},$$
then the noise vector $\boldsymbol{ n}$ must also be assumed to have dimension $N$. The same is true for the received vector $\boldsymbol{ r}$:
- $$\boldsymbol{ n} = \left(n_{1}, n_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, n_{N}\right ) \hspace{0.01cm},$$
- $$\boldsymbol{ r} = \left(r_{1}, r_{2}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, r_{N}\right )\hspace{0.05cm}.$$
The probability density function $\rm (PDF)$ for the AWGN channel is with the realization $\boldsymbol{ \eta}$ of the noise signal
- $$p_{\boldsymbol{ n}}(\boldsymbol{ \eta}) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^N } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \eta} ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm},$$
and for the conditional PDF in the maximum likelihood decision rule:
- $$p_{\hspace{0.02cm}\boldsymbol{ r}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_i) \hspace{-0.1cm} = \hspace{0.1cm} p_{\hspace{0.02cm} \boldsymbol{ n}\hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}}(\boldsymbol{ \rho} - \boldsymbol{ s}_i \hspace{0.05cm} | \hspace{0.05cm} \boldsymbol{ s}_i) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \rho} - \boldsymbol{ s}_i ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.$$
The equation follows
- from the general representation of the $N$–dimensional Gaussian PDF in the section "correlation matrix" of the book "Theory of Stochastic Signals"
- under the assumption that the components are uncorrelated (and thus statistically independent).
- $||\boldsymbol{ \eta}||$ is called the "norm" (length) of the vector $\boldsymbol{ \eta}$.
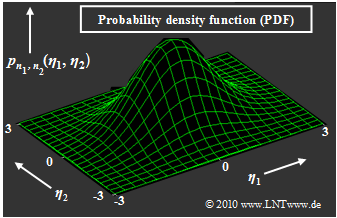
$\text{Example 3:}$ Shown on the right is the two-dimensional Gaussian probability density function $p_{\boldsymbol{ n} } (\boldsymbol{ \eta})$ of the two-dimensional random variable $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$. Arbitrary realizations of the random variable $\boldsymbol{ n}$ are denoted by $\boldsymbol{ \eta} = (\eta_1,\hspace{0.05cm}\eta_2)$. The equation of the represented two-dimensional "Gaussian bell curve" is:
- $$p_{n_1, n_2}(\eta_1, \eta_2) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{ \eta_1^2 + \eta_2^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}. $$
- The maximum of this function is at $\eta_1 = \eta_2 = 0$ and has the value $2\pi \cdot \sigma_n^2$. With $\sigma_n^2 = N_0/2$, the two-dimensional PDF in vector form can also be written as follows:
- $$p_{\boldsymbol{ n} }(\boldsymbol{ \eta}) = \frac{1}{\pi \cdot N_0 } \cdot {\rm exp} \left [ - \frac{\vert \vert \boldsymbol{ \eta} \vert \vert ^2}{N_0}\right ]\hspace{0.05cm}.$$
- This rotationally symmetric PDF is suitable e.g. for describing/investigating a "two-dimensional modulation process" such as "M–QAM", "M–PSK" or "2–FSK".
- However, two-dimensional real random variables are often represented in a one-dimensional complex way, usually in the form $n(t) = n_{\rm I}(t) + {\rm j} \cdot n_{\rm Q}(t)$. The two components are then called the "in-phase component" $n_{\rm I}(t)$ and the "quadrature component" $n_{\rm Q}(t)$ of the noise.
- The probability density function depends only on the magnitude $\vert n(t) \vert$ of the noise variable and not on angle ${\rm arc} \ n(t)$. This means: complex noise is circularly symmetric $($see graph$)$.
- Circularly symmetric also means that the in-phase component $n_{\rm I}(t)$ and the quadrature component $n_{\rm Q}(t)$ have the same distribution and thus also the same variance $($and standard deviation$)$:
- $$ {\rm E} \big [ n_{\rm I}^2(t)\big ] = {\rm E}\big [ n_{\rm Q}^2(t) \big ] = \sigma_n^2 \hspace{0.05cm},\hspace{1cm}{\rm E}\big [ n(t) \cdot n^*(t) \big ]\hspace{0.1cm} = \hspace{0.1cm} {\rm E}\big [ n_{\rm I}^2(t) \big ] + {\rm E}\big [ n_{\rm Q}^2(t)\big ] = 2\sigma_n^2 \hspace{0.05cm}.$$
Finally, some denotation variants for Gaussian random variables:
- $$x ={\cal N}(\mu, \sigma^2) \hspace{-0.1cm}: \hspace{0.3cm}\text{real Gaussian distributed random variable, with mean}\hspace{0.1cm}\mu \text { and variance}\hspace{0.15cm}\sigma^2 \hspace{0.05cm},$$
- $$y={\cal CN}(\mu, \sigma^2)\hspace{-0.1cm}: \hspace{0.12cm}\text{complex Gaussian distributed random variable} \hspace{0.05cm}.$$
Exercises for the chapter
Exercise 4.4: Maximum–a–posteriori and Maximum–Likelihood
Exercise 4.5: Irrelevance Theorem