# OVERVIEW OF THE FIFTH MAIN CHAPTER #

At the end of the book "Digital Signal Transmission", digital channel models are discussed which do not describe the transmission behavior of a digital transmission system in great detail according to the individual system components, but rather globally on the basis of typical error structures. Such channel models are mainly used for cascaded transmission systems for the inner block, if the performance of the outer system components - for example, coder and decoder - is to be determined by simulation. The following are dealt with in detail:

the descriptive variables error correlation function and error distance distribution,
the BSC model (Binary Symmetric Channel ) for the description of statistically independent errors,
the bundle error channel models according to Gilbert-Elliott and McCullough,
the Wilhelm channel model for the formulaic approximation of measured error curves,
some notes on the generation of fault sequences, for example with respect to error distance simulation,
the effects of different error structures on BMP files ⇒ images and WAV files ⇒ audios.

Note: All BMP images and WAV audios of this chapter were generated with the Windows program "Digital Channel Models & Multimedia" from the (former) practical course "Simulation of Digital Transmission Systems " at the Chair of Communications Engineering of the TU Munich.

Application of analog channel models

For investigations of message transmission systems, suitable channel models are of great importance, because they are the

prerequisite for system simulation and optimization, as well as
creating consistent and reconstructible boundary conditions.

For digital signal transmission, there are both analog and digital channel models:

Although an analog channel model does not have to reproduce the transmission channel in all physical details, it should describe its transmission behavior, including the dominant noise variables, with sufficient functional accuracy.
In most cases, a compromise must be found between mathematical manageability and the relationship to reality.

$\text{Example 1:}$ The graphic shows an analog channel model within a digital transmission system. This contains

the "channel frequency response" $H_{\rm K}(f)$ to describe the linear distortions, and
an additive noise signal $n(t)$, characterized by the "probability density function" (PDF) $f_n(n)$ and the "power-spectral density" (PSD) ${\it \Phi}_n(f)$.

Analog channel model within a digital transmission system

A special case of this model is the so-called "AWGN channel" (Additive White Gaussian Noise) with the system properties

\[H_{\rm K}(f) = 1\hspace{0.05cm},\hspace{0.2cm}{\it \Phi}_{n}(f) = {\rm const.}\hspace{0.05cm},\hspace{0.2cm} {f}_{n}(n) = \frac{1}{\sqrt{2 \pi} \cdot \sigma} \cdot {\rm e}^{-n^2\hspace{-0.05cm}/(2 \sigma^2)}\hspace{0.05cm}.\]

This simple model is suitable, for example, for describing a radio channel with time-invariant behavior, where the model is abstracted such that

the actual band-pass channel is described in the equivalent low-pass range, and

the attenuation, which depends on the frequency band and the transmission path length, is offset against the variance $\sigma^2$ of the noise signal $n(t)$.

To take time-variant characteristics into account, one must use other models such as "Rayleigh ading", "Rice fading" and "Lognormal fading", which are described in the book "Mobile communications".

For wired transmission systems, the specific frequency response of the transmission medium according to the specifications for "coaxial cable" and "two-wire line" in the book "Linear Time-Invariant Systems" must be taken into account in particular, but also the fact that white noise can no longer be assumed due to "extraneous noise" (crosstalk, electromagnetic fields, etc.).

In the case of optical systems, the multiplicatively acting, i.e. signal-dependent "shot noise" must also be suitably incorporated into the analog channel model.

Definition of digital channel models

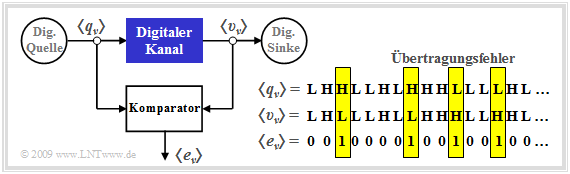
An analog channel model is characterized by analog input and output variables. In contrast, in a digital channel model (sometimes referred to as "discrete"), both the input and the output are discrete in time and value. In the following, let these be the source symbol sequence $ \langle q_\nu \rangle$ with $ q_\nu \in \{\rm L, \ H\}$ and the sink symbol sequence $ \langle v_\nu \rangle$ with $ v_\nu \in \{\rm L, \ H\}$. The indexing variable $\nu$ can take values between $1$ and $N$.

Digital channel model and exemplary sequences

As a comparison with the "block diagram" in $\text{Example 1}$ shows, the "digital channel" is a simplifying model of the analog transmission channel including the technical transmission and reception units. Simplifying because this model only refers to the occurring transmission errors, represented by the error sequence $ \langle e_\nu \rangle$ with

\[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm if}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm if}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]

While $\rm L$ and $\rm H$ denote the possible symbols, which here stand for Low and High, $ e_\nu \in \{\rm 0, \ 1\}$ is a real number value. Often the symbols are also defined as $ q_\nu \in \{\rm 0, \ 1\}$ and $ v_\nu \in \{\rm 0, \ 1\}$. To avoid confusion, we have used the somewhat unusual nomenclature here.

The error sequence $ \langle e_\nu \rangle$ given in the graph

is obtained by comparing the two binary sequences $ \langle q_\nu \rangle$ and $ \langle v_\nu \rangle$,
contains only information about the sequence of transmission errors and thus less information than an analog channel model,
is conveniently approximated by a random process with only a few parameters.

$\text{Conclusion:}$ The error sequence $ \langle e_\nu \rangle$ allows statements about the error statistics, for example whether the errors are so-called

statistically independent errors, or

bundle errors.

The following example is intended to illustrate these two types of errors.

$\text{Example 2:}$ In the following graph, we see the BMP image "White" with $300 × 200$ pixels in the center. The left image shows the falsification with statistically independent errors ⇒ "BSC model", while the right image illustrates a bundle error channel ⇒ "Gilbert-Elliott model".

BMP image "White" with independent errors or bundle errors

It should be noted that "BMP graphics" are always saved line by line, which can be seen in the error bundles in the right image.
The average error probability in both cases is $2.5\%$, which means that on average every $40$th pixel is falsified (here: white ⇒ black).

Example application of digital channel models

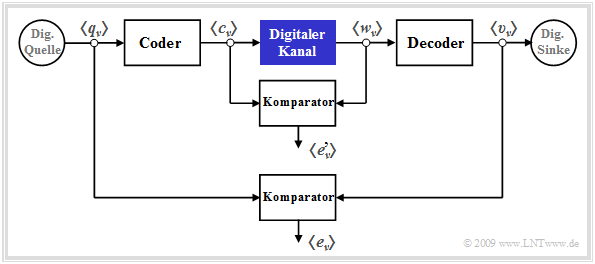
Digital channel models are preferably used for cascaded transmission, as shown in the following diagram.

Model of a transmission system with encoder/decoder

You can see from this diagram:

The inner transmission system – consisting of modulator, analog channel, noise, demodulator, receiver filter, decision and clock recovery – is summarized in the block "Digital channel" marked in blue.

This inner block is characterized exclusively by its error sequence $ \langle e\hspace{0.05cm}'_\nu \rangle$, which refers to its input symbol sequence $ \langle c_\nu \rangle$ and output symbol sequence $ \langle w_\nu \rangle$. It is obvious that this channel model provides less information than a detailed analog model considering all components.

Dagegen bezieht sich die "äußere" Fehlerfolge $ \langle e_\nu \rangle$ auf die Quellensymbolfolge $ \langle q_\nu \rangle$ und die Sinkensymbolfolge $ \langle v_\nu \rangle$ und damit auf das Gesamtsystem einschließlich der spezifischen Codierung und des empfängerseitigen Decoders.

Der Vergleich der beiden Fehlerfolgen mit und ohne Berücksichtigung von Coder/Decoder erlaubt Rückschlüsse auf die Effizienz der zugrundeliegenden Codierung und Decodierung. Diese beiden Komponenten sind dann und nur dann sinnvoll, wenn der äußere Komparator im Mittel weniger Fehler anzeigt als der innere.

Fehlerfolge und mittlere Fehlerwahrscheinlichkeit

$\text{Definition:}$ Das Übertragungsverhalten eines Binärsystems wird durch die Fehlerfolge $ \langle e_\nu \rangle$ vollständig beschrieben:

\[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]

Hieraus lässt sich die (mittlere) Bitfehlerwahrscheinlichkeit wie folgt berechnen:

\[p_{\rm M} = {\rm E}\big[e \big] = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{\nu = 1}^{N}e_{\nu}\hspace{0.05cm}.\]

Vorausgesetzt ist hierbei, dass der die Fehlentscheidungen erzeugende Zufallsprozess stationär und ergodisch ist, so dass man die Fehlerfolge $ \langle e_\nu \rangle$ formal auch durch die Zufallsgröße $e \in \{0, \ 1\}$ vollständig beschreiben kann. Der Übergang von der Zeit– zur Scharmittelung ist also zulässig.

Hinweis: In allen anderen $\rm LNTwww $–Büchern wird die mittlere Bitfehlerwahrscheinlichkeit mit $p_{\rm B}$ bezeichnet. Zur Vermeidung von Verwechslungen im Zusammenhang mit dem Gilbert–Elliott–Modell ist diese hier vorgenommene Umbenennung unvermeidbar und wir sprechen nachfolgend nicht mehr von der Bitfehlerwahrscheinlichkeit, sondern nur noch von der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$.

Fehlerkorrelationsfunktion

$\text{Definition:}$ Eine wichtige Beschreibungsgröße der digitalen Kanalmodelle ist auch die Fehlerkorrelationsfunktion – abgekürzt FKF:

\[\varphi_{e}(k) = {\rm E}\big [e_{\nu} \cdot e_{\nu + k}\big ] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.\]

Diese weist folgende Eigenschaften auf:

$\varphi_{e}(k) $ gibt die (zeitdiskrete) Autokorrelationsfunktion der ebenfalls zeitdiskreten Zufallsgröße $e$ an. Die überstreichende Linie in der rechten Gleichung kennzeichnet die Zeitmittelung.

Der Fehlerkorrelationswert $\varphi_{e}(k) $ liefert statistische Aussagen bezüglich zwei um $k$ auseinander liegende Folgenelemente, zum Beispiel über $e_{\nu}$ und $e_{\nu+ k}$. Die dazwischen liegenden Elemente $e_{\nu+ 1}$, ... , $e_{\nu+ k-1}$ beeinflussen den $\varphi_{e}(k)$–Wert nicht.

Bei stationren Folgen gilt unabhängig von der der Fehlerstatistik wegen $e \in \{0, \ 1\}$ stets:

\[\varphi_{e}(k = 0) = {\rm E}\big[e_{\nu} \cdot e_{\nu}\big] = {\rm E}\big[e^2\big]= {\rm E}\big[e\big]= {\rm Pr}(e = 1)= p_{\rm M}\hspace{0.05cm},\]

\[\varphi_{e}(k \rightarrow \infty) = {\rm E}\big[e_{\nu}\big] \cdot {\rm E}\big[e_{\nu + k}\big] = p_{\rm M}^2\hspace{0.05cm}.\]

Die Fehlerkorrelationsfunktion ist eine zumindest schwach abfallende Funktion. Je langsamer der Abfall der FKF–Werte erfolgt, desto länger ist das Gedächtnis des Kanals und um so weiter reichen die statistischen Bindungen der Fehlerfolge.

$\text{Beispiel 3:}$ Bei einer Binärübertragung werden $100$ der insgesamt $N = 10^5$ übertragenen Binärsymbole verfälscht, so dass die Fehlerfolge $ \langle e_\nu \rangle$ aus $100$ Einsen und $99900$ Nullen besteht.

Die mittlere Fehlerwahrscheinlichkeit beträgt somit $p_{\rm M} =10^{-3}$.
Die Fehlerkorrelationsfunktion $\varphi_{e}(k)$ beginnt bei $p_{\rm M} =10^{-3}$ $($für $k = 0)$ und tendiert für sehr große $k$–Werte gegen $p_{\rm M}^2 =10^{-6}$ $($für $k = \to \infty)$.
Über den tatsächlichen Verlauf von $\varphi_{e}(k)$ ist mit den hier gemachten Angaben bisher noch keine Aussage möglich.

Zusammenhang zwischen Fehlerfolge und Fehlerabstand

Zur Definition des Fehlerabstands

$\text{Definition:}$ Als Fehlerabstand $a$ bezeichnet man die Anzahl der zwischen zwei Kanalfehlern richtig übertragenen Symbole plus $1$.

Die Grafik verdeutlicht diese Definition.

Jede in der Fehlerfolge $ \langle e_\nu \rangle$ enthaltene Information über das Übertragungsverhalten des digitalen Kanals ist auch in der Folge $ \langle a_n \rangle$ der Fehlerabstände enthalten.
Da die Folgen $ \langle e_\nu \rangle$ und $ \langle a_n \rangle$ nicht synchron laufen, verwenden wir unterschiedliche Indizes $(\nu$ bzw. $n)$.

Aus der Grafik erkennt man insbesondere:

Da das erste Symbol richtig übertragen wurde $(e_1 = 0)$ und das zweite falsch $(e_2 = 1)$, ist der Fehlerabstand $a_1 = 2$.

$a_2 = 4$ sagt aus, dass zwischen den beiden ersten Fehlern $(e_2 = 1, \ e_5 = 1)$ drei Symbole richtig übertragen wurden.

Folgen zwei Fehler direkt aufeinander, so ist der Fehlerabstand wie $a_3$ in obiger Grafik gleich $1$.

Das Ereignis "$a = k$" bedeutet gleichzeitig $k-1$ fehlerfreie Symbole zwischen zwei Fehlern.
Ist zum Zeitpunkt $\nu$ ein Fehler aufgetreten, so folgt bei "$a = k$" der nächste Fehler genau zum Zeitpunkt $\nu + k$.

Der Wertevorrat der Zufallsgröße $a$ ist die Menge der natürlichen Zahlen im Gegensatz zur binären Zufallsgröße $e$:

\[a \in \{ 1, 2, 3, ... \}\hspace{0.05cm}, \hspace{0.5cm}e \in \{ 0, 1 \}\hspace{0.05cm}.\]

Die mittlere Fehlerwahrscheinlichkeit lässt sich aus beiden Zufallsgrößen ermitteln:

\[{\rm E}\big[e \big] = {\rm Pr}(e = 1) =p_{\rm M}\hspace{0.05cm}, \hspace{0.5cm} {\rm E}\big[a \big] = \sum_{k = 1}^{\infty} k \cdot {\rm Pr}(a = k) = {1}/{p_{\rm M}}\hspace{0.05cm}.\]

$\text{Beispiel 4:}$ In der skizzierten Folge sind $16$ der insgesamt $N = 40$ Symbole verfälscht ⇒ $p_{\rm M} = 0.4$. Der Erwartungswert der Fehlerabstände ergibt entsprechend

\[{\rm E}\big[a \big] = 1 \cdot {4}/{16}+ 2 \cdot {5}/{16}+ 3 \cdot {4}/{16}+4 \cdot {1}/{16}+5 \cdot {2}/{16}= 2.5 = {1}/{p_{\rm M} }\hspace{0.05cm}.\]

Fehlerabstandsverteilung

Die Wahrscheinlichkeitsdichtefunktion (WDF) der diskreten Zufallsgröße $a \in \{1, 2, 3, \text{...}\}$ setzt sich entsprechend dem Kapitel WDF-Definition für diskrete Zufallsgrößen im Buch "Stochastische Signaltheorie" aus einer (unendlichen) Summe von Diracfunktionen zusammen:

\[f_a(a) = \sum_{k = 1}^{\infty} {\rm Pr}(a = k) \cdot \delta (a-k)\hspace{0.05cm}.\]

Wir bezeichnen diese spezielle WDF als Fehlerabstandsdichtefunktion. Die Wahrscheinlichkeit, dass der Fehlerabstand $a$ exakt gleich $k$ ist, lässt sich anhand der Fehlerfolge durch die folgende bedingte Wahrscheinlichkeit ausdrücken:

\[{\rm Pr}(a = k) = {\rm Pr}(e_{\nu + 1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm} \text{...} \hspace{0.15cm}\cap \hspace{0.15cm}\hspace{0.05cm} e_{\nu + k -1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm}e_{\nu + k} = 1 \hspace{0.1cm}| \hspace{0.1cm} e_{\nu } = 1)\hspace{0.05cm}.\]

Im Buch "Stochastische Signaltheorie" finden Sie ebenfalls die Definition der Verteilungsfunktion der diskreten Zufallsgröße $a$:

\[F_a(k) = {\rm Pr}(a \le k) \hspace{0.05cm}.\]

Diese Funktion ergibt sich aus der WDF $f_a(a)$ durch Integration von $1$ bis $k$. Die Funktion $F_a(k)$ kann Werte zwischen $0$ und $1$ (einschließlich dieser beiden Grenzen) annehmen und ist schwach monoton ansteigend.

Im Zusammenhang mit den digitalen Kanalmodellen wird in der Literatur von dieser üblichen Definition abgewichen.

$\text{Definition:}$ Vielmehr gibt hier die Fehlerabstandsverteilung (FAV) die Wahrscheinlichkeit an, dass der Fehlerabstand $a$ größer oder gleich $k$ ist:

\[V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}.\]

Insbesondere gilt:

$$V_a(k = 1) = 1 \hspace{0.05cm},\hspace{0.5cm} \lim_{k \rightarrow \infty}V_a(k ) = 0 \hspace{0.05cm}.$$

Zwischen der monoton ansteigenden Funktion $F_a(k)$ und der monoton abfallenden Funktion $V_a(k)$ gilt folgender Zusammenhang:

\[F_a(k ) = 1-V_a(k +1) \hspace{0.05cm}.\]

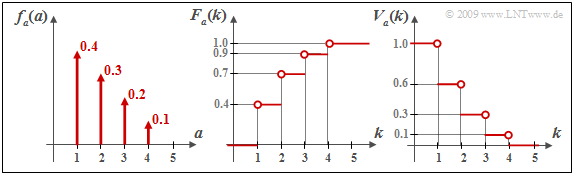
Diskrete Wahrscheinlichkeitsdichte und Verteilungsfunktionen

$\text{Beispiel 5:}$ Die Grafik zeigt in der linken Skizze eine willkürliche diskrete Fehlerabstandsdichtefunktion $f_a(a)$ und die daraus resultierenden kumulativen Funktionen

$F_a(k ) = {\rm Pr}(a \le k)$ ⇒ mittlere Skizze, sowie
$V_a(k ) = {\rm Pr}(a \ge k)$ ⇒ rechte Skizze.

Beispielsweise ergibt sich für $k = 2$:

\[F_a( k =2 ) = {\rm Pr}(a = 1) + {\rm Pr}(a = 2) \hspace{0.05cm}, \]

\[\Rightarrow \hspace{0.3cm} F_a( k =2 ) = 1-V_a(k = 3)= 0.7\hspace{0.05cm}, \]

\[ V_a(k =2 ) = 1 - {\rm Pr}(a = 1) \hspace{0.05cm},\]

\[\Rightarrow \hspace{0.3cm} V_a(k =2 ) = 1-F_a(k = 1) = 0.6\hspace{0.05cm}.\]

Für $k = 4$ erhält man folgende Resultate:

\[F_a(k = 4 ) = {\rm Pr}(a \le 4) = 1 \hspace{0.05cm}, \hspace{0.5cm} V_a(k = 4 ) = {\rm Pr}(a \ge 4)= {\rm Pr}(a = 4) = 0.1 = 1-F_a(k = 3) \hspace{0.05cm}.\]

Aufgaben zum Kapitel

Aufgabe 5.1: Fehlerabstandsverteilung

Aufgabe 5.2: Fehlerkorrelationsfunktion

Parameters of Digital Channel Models

Contents