Difference between revisions of "Digital Signal Transmission/Carrier Frequency Systems with Coherent Demodulation"
| Line 8: | Line 8: | ||
== Signal space representation of linear modulation == | == Signal space representation of linear modulation == | ||
<br> | <br> | ||
| − | In the first three chapters of this [[Digital_Signal_Transmission| | + | In the first three chapters of this [[Digital_Signal_Transmission|fourth main chapter:]] "Generalized Description of Digital Modulation Methods", the structure of the optimal receiver and the signal representation by means of basis functions were treated by the example of baseband transmission. |
| − | With the same systematics and the same uniformity, band–pass systems will now also be considered which have already been described in earlier books or chapters, namely | + | [[File:P ID2051 Dig T 4 4 S1 version2.png|right|frame|Equivalent low-pass model of carrier-modulated transmission methods '''Korrektur'''|class=fit]] |
| − | *in the main chapter 4: "Digital Modulation Methods" of the book [[Modulationsverfahren|"Modulation Methods"]],<br> | + | |
| + | With the same systematics and the same uniformity, band–pass systems will now also be considered which have already been described in earlier books or chapters, namely | ||
| + | *in the main chapter 4: "Digital Modulation Methods" of the book [[Modulationsverfahren|"Modulation Methods"]],<br> | ||
*in the chapter [[Digital_Signal_Transmission/Lineare_digitale_Modulation_–_Kohärente_Demodulation|"Linear Digital Modulation - Coherent Demodulation"]] of the present book.<br><br> | *in the chapter [[Digital_Signal_Transmission/Lineare_digitale_Modulation_–_Kohärente_Demodulation|"Linear Digital Modulation - Coherent Demodulation"]] of the present book.<br><br> | ||
| − | In the following, we restrict ourselves to ''linear modulation methods'' and ''coherent demodulation''. This means that | + | In the following, we restrict ourselves to '''linear modulation methods''' and '''coherent demodulation'''. This means that "the receiver must know exactly the frequency and phase of the carrier signal added to the transmitter". |
| − | In the | + | In the following chapter [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation|"Carrier Frequency Systems with Non-Coherent Demodulation"]] are discussed. |
| − | [[ | + | In the case of coherent demodulation, the entire transmission system can be described in the [[Modulation_Methods/Quadrature_Amplitude_Modulation#System_description_using_the_equivalent_low-pass_signal| "equivalent low-pass domain"]], and the relationship to baseband transmission is even more obvious than when band-pass signals are considered. |
| − | This results in the sketched model. Complex quantities are marked by a yellow filled double arrow. It should be noted with regard to this graph: <br> | + | This results in the sketched model. Complex quantities are marked by a yellow filled double arrow. It should be noted with regard to this graph: <br> |
| − | *From the incoming bit stream $\langle q_k \rangle \in \{\rm 0, \ L \}$, $b$ data bits each are converted serially/parallel. These output bits result in the message $m \in \{m_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, m_{M-1} \}$, where $M = 2^b$ indicates the level number. For the following, the message $m = m_i$ is assumed.<br> | + | *From the incoming bit stream $\langle q_k \rangle \in \{\rm 0, \ L \}$, $b$ data bits each are converted serially/parallel. These output bits result in the message $m \in \{m_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, m_{M-1} \}$, where $M = 2^b$ indicates the level number. For the following, the message $m = m_i$ is assumed.<br> |
| − | *In the '''signal space allocation''', a complex amplitude coefficient $a_i = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i}$ is assigned to each message $m_i$, whose real part will form the in-phase component and whose imaginary part will form the quadrature component of the later transmitted signal.<br> | + | *In the '''signal space allocation''', a complex amplitude coefficient $a_i = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i}$ is assigned to each message $m_i$, whose real part will form the "in-phase component" and whose imaginary part will form the "quadrature component" of the later transmitted signal.<br> |
| − | *At the output of the blue marked block '''generation of the | + | *At the output of the blue marked block '''generation of the low-pass signal''' the (in general) complex-valued [[Signal_Representation/Equivalent_Low-Pass_Signal_and_its_Spectral_Function|"equivalent low-pass signal"]] is present, where $g_s(t)$ shall be limited for the time being to the range $ 0 \le t \le T$ just like $s_{\rm TP}(t)$. The index $i$ again provides an indication of the message $m_i$ sent: |
::<math>s_{\rm TP}(t) \big {|}_{m \hspace{0.05cm}= \hspace{0.05cm} m_i} = a_i \cdot g_s(t) = a_{{\rm I}i} \cdot g_s(t) + {\rm j} \cdot a_{{\rm Q}i} \cdot g_s(t)</math> | ::<math>s_{\rm TP}(t) \big {|}_{m \hspace{0.05cm}= \hspace{0.05cm} m_i} = a_i \cdot g_s(t) = a_{{\rm I}i} \cdot g_s(t) + {\rm j} \cdot a_{{\rm Q}i} \cdot g_s(t)</math> | ||
*By energy normalization one gets from the basic transmission pulse $g_s(t)$ to the basis function | *By energy normalization one gets from the basic transmission pulse $g_s(t)$ to the basis function | ||
| − | : | + | :$$\varphi_1(t) = { g_s(t)}/{\sqrt{E_{gs}}} \hspace{0.4cm} {\rm with} \hspace{0.4cm} E_{gs} = |
| − | \int_{0}^{T} g_s(t)^2 \,{\rm d} t \hspace{0.3cm} | + | \int_{0}^{T} g_s(t)^2 \,{\rm d} t$$ |
| + | :$$ \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} s_{\rm TP}(t) \big {|}_{m\hspace{0.05cm} =\hspace{0.05cm} m_i} = s_{{\rm I}i} \cdot \varphi_1(t) + s_{{\rm Q}i} \cdot {\rm j} \cdot \varphi_1(t) | \Rightarrow \hspace{0.3cm} s_{\rm TP}(t) \big {|}_{m\hspace{0.05cm} =\hspace{0.05cm} m_i} = s_{{\rm I}i} \cdot \varphi_1(t) + s_{{\rm Q}i} \cdot {\rm j} \cdot \varphi_1(t) | ||
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$ |
| − | *While the coefficients $a_{{\rm I}i}$ and $a_{{\rm Q}i}$ are dimensionless, the new coefficients $s_{{\rm I}i}$ and $s_{{\rm Q}i}$ have the unit "root of energy" ⇒ see page [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#Nomenclature_in_the_fourth_chapter|"Nomenclature in the fourth chapter"]]: | + | *While the coefficients $a_{{\rm I}i}$ and $a_{{\rm Q}i}$ are dimensionless, the new coefficients $s_{{\rm I}i}$ and $s_{{\rm Q}i}$ have the unit "root of energy" ⇒ see page [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#Nomenclature_in_the_fourth_chapter|"Nomenclature in the fourth main chapter"]]: |
| − | : | + | :$$s_{{\rm I}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm I}i}\hspace{0.05cm}, $$ |
| + | :$$ s_{{\rm Q}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm Q}i}\hspace{0.05cm}. $$ | ||
| − | *The equations show that the system considered here is completely described in the equivalent TP domain by one real basis function $\varphi_1(t)$ and one purely imaginary basis function $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$ each, or by a single complex basis function $\xi_1(t)$. <br> | + | *The equations show that the system considered here is completely described in the equivalent low-pass $($German: "Tiefpass" ⇒ "TP"$)$ domain by one real basis function $\varphi_1(t)$ and one purely imaginary basis function $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$ each, or by a single complex basis function $\xi_1(t)$. <br> |
| − | *The gray shaded part | + | *The gray shaded part shows the model for generating the band-pass signal $s_{\rm BP}(t)$, first the generation of the [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function|"analytical signal"]] $s_{\rm +}(t) = s_{\rm TP}(t) \cdot {\rm e}^{{\rm j}2\pi \cdot f_{\rm T} \cdot T}$ and then the real part formation.<br> |
| − | *The two basis functions of the band-pass signal $s_{\rm BP}(t)$ result here as energy-normalized and time-limited to the range $0 \le t \le T$ cosine and minus-sine oscillations, respectively.<br><br> | + | *The two basis functions of the band-pass signal $s_{\rm BP}(t)$ result here as energy-normalized and time-limited to the range $0 \le t \le T$ cosine and minus-sine oscillations, respectively.<br><br> |
== Coherent demodulation and optimal receiver == | == Coherent demodulation and optimal receiver == | ||
<br> | <br> | ||
| − | In the following, we always assume the equivalent low-pass signal unless explicitly stated otherwise. In particular, the signals $s(t) = s_{\rm TP}(t)$ and $r(t) = r_{\rm TP}(t)$ | + | In the following, we always assume the equivalent low-pass signal unless explicitly stated otherwise. In particular, the signals |
| + | [[File:P ID2053 Dig T 4 4 S2 version1.png|right|frame|AWGN channel model for complex signals '''Korrektur'''|class=fit]] | ||
| + | |||
| + | *$s(t) = s_{\rm TP}(t)$ and | ||
| + | |||
| + | *$r(t) = r_{\rm TP}(t)$ | ||
| − | + | ||
| + | in the graph are "low-pass signals" and thus generally complex. The suffix "TP" is omitted in the remainder of this paper.<br> | ||
To this figure is to be noted: | To this figure is to be noted: | ||
| − | *The phase delay of the channel (i.e. a phase function increasing linearly with frequency) is expressed in the low-pass range by the time-independent rotation factor ${\rm e}^{{\rm j}\hspace{0.05cm} \phi}$. <br> | + | *The phase delay of the channel $($i.e. a phase function increasing linearly with frequency$)$ is expressed in the low-pass range by the time-independent rotation factor ${\rm e}^{{\rm j}\hspace{0.05cm} \phi}$. <br> |
| − | *The signal $n\hspace{0.05cm}'(t)$ describes a complex white Gaussian random process in the | + | *The signal $n\hspace{0.05cm}'(t)$ describes a complex white Gaussian random process in the low-pass domain, as given in the section [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#N-dimensional_Gaussian_noise|"N-dimensional Gaussian noise"]]. The apostrophe was added in order to be able to work with $n(t)$ later in the overall system.<br> |
| − | *The receiver knows the channel phase $\phi$ and corrects it by the conjugate-complex rotation factor ${\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$. Thus the received signal in the equivalent low-pass range is: | + | *The receiver knows the channel phase $\phi$ and corrects it by the conjugate-complex rotation factor ${\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$. Thus, the received signal in the equivalent low-pass range is: |
::<math>r(t) = s(t) + n\hspace{0.05cm}'(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\phi}= s(t) + n(t) \hspace{0.05cm}.</math> | ::<math>r(t) = s(t) + n\hspace{0.05cm}'(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\phi}= s(t) + n(t) \hspace{0.05cm}.</math> | ||
| − | *The phase rotation does not change the properties of the circular symmetric noise ⇒ $n(t) = n\hspace{0.05cm}'(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$ has exactly the same statistical properties as $n\hspace{0.05cm}'(t)$. | + | *The phase rotation does not change the properties of the circular symmetric noise ⇒ $n(t) = n\hspace{0.05cm}'(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$ has exactly the same statistical properties as $n\hspace{0.05cm}'(t)$. The left graphic in the figure above illustrates the facts just described. |
| − | + | :#The right graph shows the overall system as used for the rest of the fourth main chapter. | |
| − | The left graphic in the figure above illustrates the facts just described. | + | :#The AWGN channel is followed by an optimal receiver according to the section [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#N-dimensional_Gaussian_noise|"N-dimensional Gaussian noise"]]. |
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ A '''symbol error''' occurs whenever $\hat{m}$ does not match the message $m$ | + | $\text{Definition:}$ A '''symbol error''' occurs whenever $\hat{m}$ does not match the sent message $m$: |
::<math>m = m_i \hspace{0.2cm} \cap \hspace{0.2cm} \hat{m} \ne m_i \hspace{0.05cm}.</math>}} | ::<math>m = m_i \hspace{0.2cm} \cap \hspace{0.2cm} \hat{m} \ne m_i \hspace{0.05cm}.</math>}} | ||
| Line 76: | Line 84: | ||
The simplest digital modulation method is <i>On–off keying</i> (OOK), which has already been described in detail in the book [[Modulation_Methods/Linear_Digital_Modulation#ASK_.E2.80.93_Amplitude_Shift_Keying|"Modulation Methods"]] on the basis of its band-pass signals. There this method was partly also called <i>Amplitude Shift Keying</i> (2–ASK).<br> | The simplest digital modulation method is <i>On–off keying</i> (OOK), which has already been described in detail in the book [[Modulation_Methods/Linear_Digital_Modulation#ASK_.E2.80.93_Amplitude_Shift_Keying|"Modulation Methods"]] on the basis of its band-pass signals. There this method was partly also called <i>Amplitude Shift Keying</i> (2–ASK).<br> | ||
| − | [[File:P ID2054 Dig T 4 4 S3 version1.png| | + | [[File:P ID2054 Dig T 4 4 S3 version1.png|right|frame|Signal space constellations for on-off keying|class=fit]] |
This method can be characterized as follows: | This method can be characterized as follows: | ||
Revision as of 15:51, 31 July 2022
Contents
- 1 Signal space representation of linear modulation
- 2 Coherent demodulation and optimal receiver
- 3 On–off keying (2–ASK)
- 4 Binary phase shift keying (BPSK)
- 5 M–level amplitude shift keying (M–ASK)
- 6 Quadrature amplitude modulation (M-QAM)
- 7 Multi-level phase–shift keying (M–PSK)
- 8 Binary frequency shift keying (2–FSK)
- 9 Minimum Shift Keying (MSK)
- 10 Exercises for the chapter
- 11 References
Signal space representation of linear modulation
In the first three chapters of this fourth main chapter: "Generalized Description of Digital Modulation Methods", the structure of the optimal receiver and the signal representation by means of basis functions were treated by the example of baseband transmission.
With the same systematics and the same uniformity, band–pass systems will now also be considered which have already been described in earlier books or chapters, namely
- in the main chapter 4: "Digital Modulation Methods" of the book "Modulation Methods",
- in the chapter "Linear Digital Modulation - Coherent Demodulation" of the present book.
In the following, we restrict ourselves to linear modulation methods and coherent demodulation. This means that "the receiver must know exactly the frequency and phase of the carrier signal added to the transmitter".
In the following chapter "Carrier Frequency Systems with Non-Coherent Demodulation" are discussed.
In the case of coherent demodulation, the entire transmission system can be described in the "equivalent low-pass domain", and the relationship to baseband transmission is even more obvious than when band-pass signals are considered.
This results in the sketched model. Complex quantities are marked by a yellow filled double arrow. It should be noted with regard to this graph:
- From the incoming bit stream $\langle q_k \rangle \in \{\rm 0, \ L \}$, $b$ data bits each are converted serially/parallel. These output bits result in the message $m \in \{m_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, m_{M-1} \}$, where $M = 2^b$ indicates the level number. For the following, the message $m = m_i$ is assumed.
- In the signal space allocation, a complex amplitude coefficient $a_i = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i}$ is assigned to each message $m_i$, whose real part will form the "in-phase component" and whose imaginary part will form the "quadrature component" of the later transmitted signal.
- At the output of the blue marked block generation of the low-pass signal the (in general) complex-valued "equivalent low-pass signal" is present, where $g_s(t)$ shall be limited for the time being to the range $ 0 \le t \le T$ just like $s_{\rm TP}(t)$. The index $i$ again provides an indication of the message $m_i$ sent:
- \[s_{\rm TP}(t) \big {|}_{m \hspace{0.05cm}= \hspace{0.05cm} m_i} = a_i \cdot g_s(t) = a_{{\rm I}i} \cdot g_s(t) + {\rm j} \cdot a_{{\rm Q}i} \cdot g_s(t)\]
- By energy normalization one gets from the basic transmission pulse $g_s(t)$ to the basis function
- $$\varphi_1(t) = { g_s(t)}/{\sqrt{E_{gs}}} \hspace{0.4cm} {\rm with} \hspace{0.4cm} E_{gs} = \int_{0}^{T} g_s(t)^2 \,{\rm d} t$$
- $$ \hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm TP}(t) \big {|}_{m\hspace{0.05cm} =\hspace{0.05cm} m_i} = s_{{\rm I}i} \cdot \varphi_1(t) + s_{{\rm Q}i} \cdot {\rm j} \cdot \varphi_1(t) \hspace{0.05cm}.$$
- While the coefficients $a_{{\rm I}i}$ and $a_{{\rm Q}i}$ are dimensionless, the new coefficients $s_{{\rm I}i}$ and $s_{{\rm Q}i}$ have the unit "root of energy" ⇒ see page "Nomenclature in the fourth main chapter":
- $$s_{{\rm I}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm I}i}\hspace{0.05cm}, $$
- $$ s_{{\rm Q}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm Q}i}\hspace{0.05cm}. $$
- The equations show that the system considered here is completely described in the equivalent low-pass $($German: "Tiefpass" ⇒ "TP"$)$ domain by one real basis function $\varphi_1(t)$ and one purely imaginary basis function $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$ each, or by a single complex basis function $\xi_1(t)$.
- The gray shaded part shows the model for generating the band-pass signal $s_{\rm BP}(t)$, first the generation of the "analytical signal" $s_{\rm +}(t) = s_{\rm TP}(t) \cdot {\rm e}^{{\rm j}2\pi \cdot f_{\rm T} \cdot T}$ and then the real part formation.
- The two basis functions of the band-pass signal $s_{\rm BP}(t)$ result here as energy-normalized and time-limited to the range $0 \le t \le T$ cosine and minus-sine oscillations, respectively.
Coherent demodulation and optimal receiver
In the following, we always assume the equivalent low-pass signal unless explicitly stated otherwise. In particular, the signals
- $s(t) = s_{\rm TP}(t)$ and
- $r(t) = r_{\rm TP}(t)$
in the graph are "low-pass signals" and thus generally complex. The suffix "TP" is omitted in the remainder of this paper.
To this figure is to be noted:
- The phase delay of the channel $($i.e. a phase function increasing linearly with frequency$)$ is expressed in the low-pass range by the time-independent rotation factor ${\rm e}^{{\rm j}\hspace{0.05cm} \phi}$.
- The signal $n\hspace{0.05cm}'(t)$ describes a complex white Gaussian random process in the low-pass domain, as given in the section "N-dimensional Gaussian noise". The apostrophe was added in order to be able to work with $n(t)$ later in the overall system.
- The receiver knows the channel phase $\phi$ and corrects it by the conjugate-complex rotation factor ${\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$. Thus, the received signal in the equivalent low-pass range is:
- \[r(t) = s(t) + n\hspace{0.05cm}'(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\phi}= s(t) + n(t) \hspace{0.05cm}.\]
- The phase rotation does not change the properties of the circular symmetric noise ⇒ $n(t) = n\hspace{0.05cm}'(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$ has exactly the same statistical properties as $n\hspace{0.05cm}'(t)$. The left graphic in the figure above illustrates the facts just described.
- The right graph shows the overall system as used for the rest of the fourth main chapter.
- The AWGN channel is followed by an optimal receiver according to the section "N-dimensional Gaussian noise".
$\text{Definition:}$ A symbol error occurs whenever $\hat{m}$ does not match the sent message $m$:
- \[m = m_i \hspace{0.2cm} \cap \hspace{0.2cm} \hat{m} \ne m_i \hspace{0.05cm}.\]
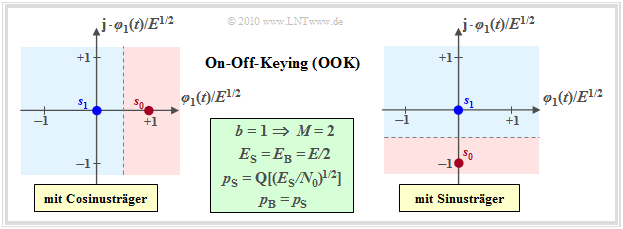
On–off keying (2–ASK)
The simplest digital modulation method is On–off keying (OOK), which has already been described in detail in the book "Modulation Methods" on the basis of its band-pass signals. There this method was partly also called Amplitude Shift Keying (2–ASK).
This method can be characterized as follows:
- OOK is a one-dimensional modulation method $(N = 1)$ with $s_{{\rm I}i} = \{0, E^{1/2}\}$ and $s_{{\rm Q}i} \equiv 0$ or $s_{{\rm I}i} \equiv 0$ and $s_{{\rm Q}i} = \{0, -E^{1/2}\}$. As an abbreviation, $E = E_{g_s}$. The first combination describes a cosinusoidal carrier signal, the second combination a sinusoidal carrier.
- Each bit is assigned to a binary symbol $(b = 1, \ M = 2)$; thus, no serial/parallel converter is needed. For equally probable symbols, which is always assumed for what follows, both the mean energy per symbol $(E_{\rm S})$ and the mean energy per bit $(E_{\rm B})$ are equal to $E/2$.
- The optimal OOK receiver virtually projects the complex-valued received signal $r(t)$ onto the basis function $\varphi_1(t)$, if one starts from the left sketch (cosine carrier).
- Because of $N = 1$, the noise can be one-dimensional with the variance $\sigma_n^2 = N_0/2$. Using the statements in the section "Error probability for symbols with equal probability", we obtain for the mean symbol error probability:
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{\frac{E}{2 N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.\]
- Since each bit is mapped to exactly one symbol, the average bit error probability $p_{\rm B}$ is exactly:
- \[p_{\rm B} = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.\]
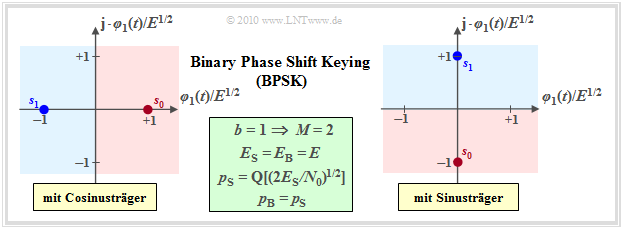
Binary phase shift keying (BPSK)
The very often used method Binary Phase Shift Keying (BPSK), which was already described in detail in the chapter "Linear Digital Modulation" of the book "Modulation Methods" using the band–pass signals (typical: phase jumps), differs from On–off keying by a constant envelope.
For the signal space points, $\boldsymbol{s}_1 = -\boldsymbol{s}_0$ always holds. For example, they are:
- $s_{{\rm I}i} = \{\pm E^{1/2}\}$ and $s_{{\rm Q}i} \equiv 0$ with a cosine carrier,
- $s_{{\rm I}i} \equiv 0$ and $s_{{\rm Q}i} = \{\pm E^{1/2}\}$ with a sinusoidal carrier.
The improvements compared to on–off keying can be seen from the equations given in the graphic (in the field with a green background):
- For a given normalization energy $E$, the distance between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$ is twice as large. This gives the error probability (both related to symbols and bits):
- \[p_{\rm S} = p_{\rm B} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{2 E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.\]
- This equation also takes into account that $E_{\rm S} = E_{\rm B} = E$ now applies, which means that the average energies per symbol or per bit are now twice as large as with OOK.
- Because of the factor $2$ under the square root in the argument of the Q function, the BPSK error probability is noticeably lower than with on–off keying if $E_{\rm S}$ and $N_0$ are not changed.
- In other words: With the same $N_0$, BPSK only requires half the symbol energy $E_{\rm S}$ in order to achieve the same error probability as on–off keying. The logarithmic gain is $3 \ \rm dB$.
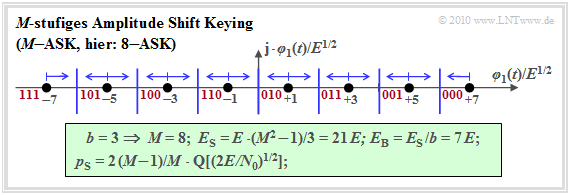
M–level amplitude shift keying (M–ASK)
In analogy to "M–level baseband transmission", we now consider $M$–level Amplitude Shift Keying ($M$–ASK), whose low-pass signal space constellation for the parameters $b = 3$ ⇒ $M = 8$ ⇒ $8$–ASK looks as follows.
The name $M$–ASK is not entirely accurate. Rather, it is a combined ASK/PSK method, since, for example, the two innermost signal space points $(\pm 1)$ do not differ in terms of amplitude (envelope), but only in terms of phase ($0^\circ$ or $180^\circ$).
It should also be noted:
- The average energy per symbol can be calculated as follows for this one-dimensional method using symmetry:
- \[E_{\rm S} = \frac{2}{M} \cdot \sum_{k = 1}^{M/2} (2k -1)^2 \cdot E = \frac{M^2 -1}{3} \cdot E \hspace{0.05cm}.\]
- Since each of the $M$ symbols represents $b = \log_2 (M)$ bits, the average energy per bit is:
- \[E_{\rm B} = \frac{E_{\rm S}}{b} = \frac{E_{\rm S}}{{\rm log_2}\, (M)} =\frac{M^2 -1}{3 \cdot {\rm log_2}\, (M)} \cdot E \hspace{0.3cm}\Rightarrow\hspace{0.3cm}M= 8\hspace{-0.1cm}: E_{\rm S}/E = 21 \hspace{0.05cm}, \hspace{0.1cm}E_{\rm B}/E = 7\hspace{0.05cm}.\]
- The probability that one of the two outer symbols is falsified due to AWGN noise is therefore the same
- \[{\rm Pr}({\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} \text{outer symbol)} = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right )\hspace{0.05cm}.\]
- The falsification probability of the $M-2$ inner symbols is twice as large, since other decision regions border on both the right and the left. By averaging one obtains for the (mean) symbol error probability:
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) = \frac{1}{M} \cdot \left [ 2 \cdot 1 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) + (M-2) \cdot 2 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \right ] \]
- \[\Rightarrow \hspace{0.3cm} p_{\rm S} = \frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) =\frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{\frac{6 \cdot E_{\rm S}}{(M^2-1) \cdot N_0}}\right ) \hspace{0.05cm}.\]
- When using the "Gray code" (neighboring symbols each differ by one bit), the bit error probability $p_{\rm B}$ is approximately the factor $b = \log_2 \ (M)$ smaller than the symbol error probability $p_{\rm S}$:
- \[p_{\rm B} \approx \frac{p_{\rm S}}{b} = \frac{2 \cdot (M-1)}{M \cdot {\rm log_2}\, (M)} \cdot {\rm Q} \left ( \sqrt{{6 \cdot {\rm log_2}\, (M)}/({M^2-1 }) \cdot { E_{\rm B}}/{ N_0}}\right ) \hspace{0.05cm}.\]
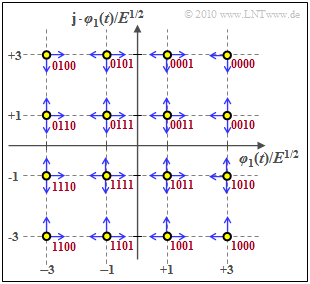
Quadrature amplitude modulation (M-QAM)
The "quadrature amplitude modulation" ($M$–QAM) results from a $M$–ASK each for in-phase and quadrature components ⇒ $M^2$ signal space points.
Each symbol now represents $b = \log_2 (M)$ binary characters (bits). The graphic shows the special case $M = 16$ ⇒ $b = 4$. The bit assignment for "Gray coding" is shown in red (neighboring symbols each differ by one bit).
The average energy per symbol $(E_{\rm S})$ or the average energy per bit $(E_{\rm B})$ can be easily derived from the result for the $M$–ASK (note the difference in the equation between an energy $E$ and the expected value $\rm E[\text{...}]$):
- \[E_{\rm S} = {\rm E} \left [ |s_{i}|^2 \right ] = {\rm E} \left [ |s_{{\rm I}i}|^2 \right ] + {\rm E} \left [ |s_{{\rm Q}i}|^2 \right ] = 2 \cdot {\rm E} \left [ |s_{{\rm I}i}|^2 \right ]\]
- \[\Rightarrow \hspace{0.3cm} E_{\rm S} = 2 \cdot \frac{M_{\rm I}^2-1}{3} \cdot E = \frac{2}{3} \cdot (M-1) \cdot E\hspace{0.01cm},\hspace{0.3cm}E_{\rm B} =\frac{2 \cdot (M-1)}{3 \cdot {\rm log_2}\, (M)} \cdot E \hspace{0.01cm}.\]
In addition, the M–level quadrature amplitude modulation shows the following properties:
- The "Union Bound" can be used as an upper bound for the symbol error probability, whereby it should be noted that an inner symbol can be falsified in four directions:
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) \le \left\{ \begin{array}{c} 4 \cdot p \\ 2 \cdot p \end{array} \right.\quad \begin{array}{*{1}c} {\rm for} \hspace{0.15cm} M \ge 16 \hspace{0.05cm}, \\ {\rm for} \hspace{0.15cm} M = 4 \hspace{0.05cm},\\ \end{array} \hspace{0.4cm} {\rm with} \hspace{0.4cm} p = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \hspace{0.05cm}.\]
- If one takes into account that only the $(b-2)^2$ inner points are falsified in four directions, in contrast, the four vertices are falsified only in two and the remaining points in three directions (blue arrows in the graphic), therefore one obtains with $M = b^2$ the better approximation
- \[p_{\rm S} \approx {1}/{M} \cdot \big [(b - 2)^2 \cdot 4p + 4 \cdot 2p + 4 \cdot (b - 2) \cdot 3p \big ] = {p}/{M} \cdot \big [ 4 \cdot M - 16 \cdot \sqrt{M} + 16 + 8 + 12 \cdot \sqrt{M} - 24\big ] \]
- \[\Rightarrow \hspace{0.3cm} p_{\rm S} \approx {4 \cdot p}/{M} \cdot \big [ M - \sqrt{M} \big ] = 4p \cdot \big [ 1 - {1}/{\sqrt{M}} \big ] \]
- \[\Rightarrow\hspace{0.3cm} M = 16\hspace{-0.1cm}: \hspace{0.1cm} p_{\rm S} \approx 3 \cdot p = 3 \cdot {\rm Q} \big ( \sqrt{{2 E}/{N_0}}\big ) = 3 \cdot {\rm Q} \big ( \sqrt{{1/5 \cdot E_{\rm S}}/{ N_0}}\big ) \hspace{0.05cm}.\]
$\text{Conclusion:}$ With $M$–QAM, $E_{\rm B} = E_{\rm S}/\log_2 \hspace{0.05cm} (M)$ generally applies and with Gray coding, $p_{\rm B} = p_{\rm S}/\log_2 \hspace{0.05cm} (M)$ is also applicable.
This gives the mean bit error probability:
- \[p_{\rm B} \approx \frac{4 \cdot (1 - 1/\sqrt{M})}{ {\rm log_2}\hspace{0.05cm} (M)} \cdot {\rm Q} \left ( \sqrt{ \frac{3 \cdot {\rm log_2}\, (M)}{M-1 } \cdot { E_{\rm B} }/{ N_0} }\right ) \hspace{0.05cm}.\]
- The approximation is exactly valid for $M \le 16$ if – as assumed for the upper graphic – no "diagonal falsifications" occur.
- The special case "4–QAM" (without inner symbols) is dealt with in "Exercise 4.13".
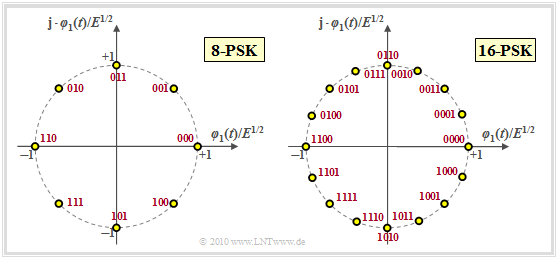
Multi-level phase–shift keying (M–PSK)
In the case of multi-level phase modulation, in which case the level number $M$ is usually a power of two in practice, all signal space points are evenly distributed on a circle with radius $E^{1/2}$. This means that $E_{\rm S} = E$ holds for the average symbol energy and $E_{\rm B} = E_{\rm S}/b = E/\hspace{-0.05cm}\log_2 \hspace{0.05cm} (M)$ for the average energy per bit.
For the in-phase and quadrature components of the signal space points $\boldsymbol{s}_i$, the general rule is $(i = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, \hspace{0.05cm}M-1)$:
- \[s_{{\rm I}i} = \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},\hspace{0.2cm} s_{{\rm Q}i} = \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} || \boldsymbol{ s}_i || = \sqrt{ s_{{\rm I}i}^2 + s_{{\rm Q}i}^2} = 1 \hspace{0.05cm}.\]
The phase offset is set to $\phi_{\rm off} = 0$ in the graphic above. The 4–PSK with $\phi_{\rm off} = \pi/4 \ (45^\circ)$ is identical to the "4–QAM". The distance between two adjacent points is the same in all cases:
- \[d_{\rm min} = d_{\rm 0, \hspace{0.05cm}1} = d_{\rm 1, \hspace{0.05cm}2} = \hspace{0.05cm}\text{...} \hspace{0.05cm} = d_{M-1, \hspace{0.05cm}0} = 2 \cdot \sqrt{E} \cdot \sin (\pi/M)\]
- \[\Rightarrow\hspace{0.3cm} M = 4\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} = \sqrt{2} \approx 1.414 \hspace{0.05cm}, \hspace{0.8cm} M = 8\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.765 \hspace{0.05cm},\hspace{0.8cm} M = 16\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.390 \hspace{0.05cm}.\]
The upper bound $p_{\rm UB}$ for the AWGN symbol error probability after the "Union Bound" yields:
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) \le 2 \cdot {\rm Q} \left ( \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right ) = p_{\rm UB} \hspace{0.05cm}.\]
One recognises:
- For $M = 2$ (BPSK) one obtains the estimate $p_{\rm S} \le p_{\rm UB} =2 \cdot {\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$. A comparison with the equation $p_{\rm S} ={\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$ given on the "BPSK section" shows that in this special case the "Union Bound" returns double the value as the upper limit.
- The larger $M$ is, the more precisely $p_{\rm UB}$ approximates the exact symbol error probability $p_{\rm S}$. an. The interactive applet "Multi-level PSK & Union Bound" also gives the more accurate error probability obtained through simulation.
$\text{Conclusion:}$ The limit for the M–PSK bit error probability is (assuming Gray code ⇒ red labeling):
- \[p_{\rm B} \le \frac{2}{ {\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{ {\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.\]
- However, this limit only has to be applied for $M > 4$.
- For $M = 2$ (BPSK) and $M = 4$ (identity between 4–PSK and 4–QAM), the bit error probability can be specified exactly:
- $$p_{\rm B} = {\rm Q} \left ( \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.$$
Binary frequency shift keying (2–FSK)
This type of modulation with parameter $b = 1$ ⇒ $M = 2$ has already been described in detail in the section "FSK – Frequency Shift Keying" of the book "Modulation Methods" using the band-pass signals.
The two possible signal forms are represented by two different frequencies in the range $0 \le t \le T$:
- \[s_{\rm BP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} + \Delta f_{\rm A})\cdot t)\hspace{0.05cm},\]
- \[ s_{\rm BP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} - \Delta f_{\rm A})\cdot t)\hspace{0.05cm}.\]
$f_{\rm T}$ designates the carrier frequency and $\Delta f_{\rm A}$ the (one-sided) frequency deviation. The average energy per symbol or per bit is the same in each case:
- \[E_{\rm S} = E_{\rm B} = E = \frac{A^2 \cdot T}{2} \hspace{0.05cm}.\]
The FSK in the equivalent low-pass signal space is now to be considered here. Then:
- \[s_{\rm TP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]
- \[ s_{\rm TP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]
and for the inner product one obtains
- \[< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \hspace{-0.1cm} \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t = A^2 \cdot \int_{0}^{T} {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t} \,{\rm d} t = \frac{A^2}{{\rm j} \cdot 4\pi \cdot \Delta f_{\rm A}} \cdot \big [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot T} - 1 \big ] \hspace{0.05cm}.\]
$\text{Definition:}$ The modulation index $h = 2 \cdot \Delta f_{\rm A}\hspace{0.03cm}\cdot T$ is the ratio between the total (bilateral) frequency deviation $(2 \cdot \Delta f_{\rm A})$ and the symbol rate $(1/T)$.
The two signals are then orthogonal if this inner product is equal to zero:
- \[< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \frac{A^2\cdot T}{{\rm j} \cdot 2\pi \cdot h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2h} - 1 \right ] = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T = 1,\hspace{0.1cm} 2, \hspace{0.1cm}3,\ \text{ ... }\hspace{0.05cm}.\]
If the modulation index $h$ is assumed to be an integer, the low-pass signals can be written in the form
- \[s_{\rm TP0}(t) = \sqrt{E} \cdot \xi_1(t) \hspace{0.05cm},\]
- \[s_{\rm TP1}(t) = \sqrt{E} \cdot \xi_2(t)\]
with complex basis functions:
- \[\xi_1(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]
- \[ \xi_2(t)= \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.\]
The result is the signal space representation of the binary FSK outlined here.
$\text{Conclusion:}$
- With an integer modulation index $h$, the low-pass signals $s_{\rm TP0}(t)$ and $s_{\rm TP1}(t)$ of the binary FSK are orthogonal to one another.
- This results in the symbol error probability (derivation in the graphic):
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q} \left ( \sqrt{ { {E_{\rm S} } }/{ N_0} }\right ) \hspace{0.05cm}.\]
- The bit error probability has the same value: $p_{\rm B} = p_{\rm S}$.
Note: In contrast to the representation in [KöZ08][1], the frequency deviation $\Delta f_{\rm A}$ is defined here on one side. Therefore, the equations sometimes differ by a factor of $2$. However, if you work with the modulation index $h$, there are no differences.
Minimum Shift Keying (MSK)
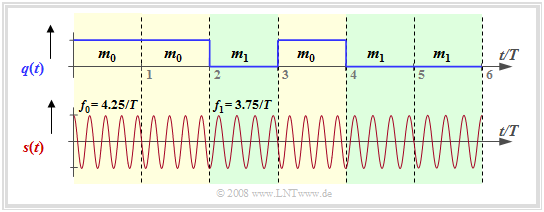
"Minimum Shift Keying" (MSK) is a binary FSK system with the modulation index $h = 0.5$ ⇒ frequency deviation $\Delta f_{\rm A} = 1/(2T)$. The graphic shows an MSK signal for the carrier frequency $ f_{\rm T} = 4/T$:
- The two frequencies within the transmission signal are $ f_{\rm 0} = f_{\rm T} + 1/(4T)$ to represent the message $m_0$ (yellow background) and $ f_{\rm 1} = f_{\rm T} -1/(4T)$ ⇒ message $m_1$ (green background).
- The graph also accounts for continuous phase adjustment at the transitions to further reduce the signal bandwidth. This is then referred to as "Continuous Phase Modulation" (CPM).
Without this phase adjustment, the two band-pass waveforms are:
- \[s_{\rm BP0}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]
- \[ s_{\rm BP1}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm}.\]
If you form the inner product of the band-pass signals, you get with $f_{\rm \Delta} = f_0 - f_1$ and $f_{\rm \Sigma} = f_0 + f_1$:
- \[< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {2E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_0 t) \cdot \cos( 2\pi f_1 t)\,{\rm d} t = {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Delta} t) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Sigma} t) \,{\rm d} t\]
- \[ \Rightarrow \hspace{0.3cm}< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm} \cos( \pi \cdot {t}/{T}) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm}\cos( 2\pi \cdot 2 f_{\rm T} \cdot t) \,{\rm d} t \hspace{0.05cm}.\]
The first integral is zero $($integral over "cosine" from $0$ to $\pi)$. For $f_{\rm T} \gg 1/T$, which can be assumed in practice, the second integral also vanishes. This gives the inner product:
- $$< \hspace{0.02cm} s_{\rm BP0}(t) \cdot s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm}= 0 \hspace{0.05cm}.$$
$\text{Conclusion:}$
- This shows that the two band-pass signals are orthogonal for the modulation index $h = 0.5$ (i.e. MSK) and all multiples thereof.
- With the new real basis functions
- \[\varphi_1(t) = \sqrt{2/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]
- \[ \varphi_2(t) = \sqrt{2/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\]
- one obtains exactly the same signal space constellation as for even-numbered $h = 1, 2, 3, \ \text{ ...}$.
- This results in the same error probability:
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q} \left ( \sqrt{ { {E_{\rm S} } }/{ N_0} }\right ) = p_{\rm B} \hspace{0.05cm}.\]
Exercises for the chapter
Exercise 4.11: On-Off Keying and Binary Phase Shift Keying
Exercise 4.11Z: OOK and BPSK once again
Exercise 4.12: Calculations for the 16-QAM
Exercise 4.14: 8-PSK and 16-PSK
Exercise 4.14Z: 4-QAM and 4-PSK
Exercise 4.15: Optimal Signal Space Allocation
Exercise 4.16: Binary Frequency Shift Keying
References
- ↑ Kötter, R., Zeitler, G.: Nachrichtentechnik 2. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2008.