Difference between revisions of "Mobile Communications/Characteristics of GSM"
| (31 intermediate revisions by 3 users not shown) | |||
| Line 9: | Line 9: | ||
<br> | <br> | ||
$\rm GSM$ $\rm (G$lobal $\rm S$ystem for $\rm M$obile Communication$)$ is a strongly hierarchically structured system of different network components. You can see from the graphic: | $\rm GSM$ $\rm (G$lobal $\rm S$ystem for $\rm M$obile Communication$)$ is a strongly hierarchically structured system of different network components. You can see from the graphic: | ||
| − | [[File: | + | [[File:EN_Mob_T_3_3_S1.png|right|frame|GSM system architecture|class=fit]] |
*The mobile station $\rm (MS)$ communicates via the radio interface with the nearest base transceiver station $\rm (BTS$, transmit and receive base station).<br> | *The mobile station $\rm (MS)$ communicates via the radio interface with the nearest base transceiver station $\rm (BTS$, transmit and receive base station).<br> | ||
| Line 23: | Line 23: | ||
| − | More detailed information on GSM system architecture and the individual network components can be found in the chapter [[Examples_of_Communication_Systems/General_Description_of_GSM|General Description of GSM]] of the book "Examples of Communication Systems". | + | More detailed information on GSM system architecture and the individual network components can be found in the chapter [[Examples_of_Communication_Systems/General_Description_of_GSM|"General Description of GSM"]] of the book "Examples of Communication Systems". |
<br clear=all> | <br clear=all> | ||
== Multiple access with GSM == | == Multiple access with GSM == | ||
<br> | <br> | ||
| + | [[File:EN_Mob_T_3_3_S2_v2.png|right|frame|Realization of FDMA and TDMA with "GSM 900"|class=fit]] | ||
GSM uses two multiple access methods in parallel: | GSM uses two multiple access methods in parallel: | ||
| Line 33: | Line 34: | ||
| − | The graphic and the following description is valid for the original system "GSM 900" ( | + | The graphic and the following description is valid for the original system "GSM 900" (in the following: "GSM–D"). |
| − | + | For "GSM/DCS 1800" ⇒ "GSM–E" comparable statements apply. | |
| − | * | + | *With "GSM–D", a bandwidth of $25\ \rm MHz$ is provided for uplink and downlink respectively $($duplex spacing: $45\ \rm MHz)$. This is called "Frequency Division Duplex" $\rm (FDD)$. For "GSM–E", the bandwidth is $75\ \rm MHz$ and the duplex spacing is $95\ \rm MHz$.<br> |
| − | *Uplink and downlink bands are divided into frequency bands of width $200\ \rm kHz$. Taking into account the protection areas at the respective edges, there are $N_{\rm F} = 124$ (GSM–D | + | *Uplink and downlink bands are divided into frequency bands of width $200\ \rm kHz$. Taking into account the protection areas at the respective edges, there are $N_{\rm F} = 124$ (GSM–D) or $N_{\rm F} = 374$ (GSM–E) frequency channels. |
| − | *Each cell is assigned a subset of the frequencies ⇒ "Cell Allocation". Neighboring cells usually work at different frequencies, for example with the reuse–factor $3$, as in section [[Mobile_Communications/Similarities_Between_GSM_and_UMTS#Cellular_architecture|Cellular architecture]] indicated by the colors | + | *Each cell is assigned a subset of the frequencies ⇒ "Cell Allocation". Neighboring cells usually work at different frequencies, for example with the reuse–factor $3$, as in section [[Mobile_Communications/Similarities_Between_GSM_and_UMTS#Cellular_architecture|"Cellular architecture"]] indicated by the colors white, yellow, and blue.<br> |
*The $124$ GSM frequency channels are further divided by time division multiplexing $\rm (TDMA)$. Each FDMA channel is divided into TDMA frames, which each comprise $N_{\rm T} = 8$ time slots. | *The $124$ GSM frequency channels are further divided by time division multiplexing $\rm (TDMA)$. Each FDMA channel is divided into TDMA frames, which each comprise $N_{\rm T} = 8$ time slots. | ||
| − | *The slots are periodically assigned to the individual GSM users and each contain a so-called [[Mobile_Communications/Characteristics_of_GSM#Data_and_frame_structure_for_GSM| | + | *The slots are periodically assigned to the individual GSM users and each contain a so-called [[Mobile_Communications/Characteristics_of_GSM#Data_and_frame_structure_for_GSM|$\text{Burst}$]]. Each user has a time slot available in each TDMA frame. A bundling (maximum six per user) is only possible with GPRS/EDGE.<br> |
*The TDMA frames of the uplink are sent delayed by three slots compared to the downlink: "Time Division Duplex" $\rm (TDD)$. The hardware of the mobile station can thus be used for sending and receiving a message simultaneously. | *The TDMA frames of the uplink are sent delayed by three slots compared to the downlink: "Time Division Duplex" $\rm (TDD)$. The hardware of the mobile station can thus be used for sending and receiving a message simultaneously. | ||
| Line 52: | Line 53: | ||
== Data and frame structure for GSM == | == Data and frame structure for GSM == | ||
<br> | <br> | ||
| − | The mapping of logical to physical channels is done using the GSM frame structure. Here we only look to traffic channels and to the mapping in time. In this case, each multi–frame of $120 \ \rm ms$ duration is divided into $26$ TDMA frames (two of them for control channels) of $4 | + | The mapping of logical to physical channels is done using the GSM frame structure. Here we only look to traffic channels and to the mapping in time. In this case, each multi–frame of $120 \ \rm ms$ duration is divided into $26$ TDMA frames (two of them for control channels) of $4.615\ \rm ms$ duration. Thus, the duration of a time slot is approximately $T_{\rm Z} = 576.9\ \rm µ s$.<br> |
| − | [[File: | + | [[File:EN_Mob_T_3_3_S2_v3.png||right|frame|Data and frame structure for GSM|class=fit]] |
You can see from this graphic: | You can see from this graphic: | ||
| Line 61: | Line 62: | ||
::<math>R_{\rm total} = {1}/{T_{\rm B}}= 270.833\,{\rm kbit/s}\hspace{0.05cm}.</math> | ::<math>R_{\rm total} = {1}/{T_{\rm B}}= 270.833\,{\rm kbit/s}\hspace{0.05cm}.</math> | ||
| − | *The '''gross data rate''' of each user is | + | *The »'''gross data rate'''« of each user is $R_{\rm gross} = 33.854 \ \rm kbit/s$. But since in every normal burst only $2 · 57 = 114$ data bits (highlighted blue in the graphic) are transmitted, it results in the lower »'''net data rate'''« $R_{\rm net} = 22.8 \ \rm kbit/s$.<br> |
*This net data rate also takes the channel coding into account. In the case of a speech signal, for every $20\ \rm kbit/s$ speech frame $456$ bits are transmitted, which results in exactly the rate $R_{\rm net} = 22.8 \ \rm kbit/s$. Without channel coding, the data rate would be only $13 \ \rm kbit/s$.<br> | *This net data rate also takes the channel coding into account. In the case of a speech signal, for every $20\ \rm kbit/s$ speech frame $456$ bits are transmitted, which results in exactly the rate $R_{\rm net} = 22.8 \ \rm kbit/s$. Without channel coding, the data rate would be only $13 \ \rm kbit/s$.<br> | ||
| − | *In addition to the traffic data, a '''normal burst''' also contains | + | *In addition to the traffic data, a »'''normal burst'''« also contains |
:– twice three tailbits (red, during this time the channel is remeasured), | :– twice three tailbits (red, during this time the channel is remeasured), | ||
:– two signaling bits (green), | :– two signaling bits (green), | ||
| − | |||
:– the "Guard Period" $\rm (GP)$ with $8.25$ bit duration $($grey, ca. $30.5 \ \rm µ s)$, | :– the "Guard Period" $\rm (GP)$ with $8.25$ bit duration $($grey, ca. $30.5 \ \rm µ s)$, | ||
:– $26$ bit for a training sequence (for channel estimation and synchronization). | :– $26$ bit for a training sequence (for channel estimation and synchronization). | ||
| Line 75: | Line 75: | ||
''Note:'' | ''Note:'' | ||
| − | *In GSM, besides the "Normal Burst" there are some other [[Examples_of_Communication_Systems/Radio_Interface# | + | *In GSM, besides the "Normal Burst" there are some other [[Examples_of_Communication_Systems/Radio_Interface#The_different_burst_types_in_GSM|$\text{types of bursts}$]]: Frequency Correction Burst, Synchronization Burst, Dummy Burst, Access Burst, ... . |
| − | *All these bursts have a uniform length of $156.25$ bit durations. This is discussed in more detail in the [[Aufgaben:Exercise_3.2:_GSM Data Rates|Excercise 3.2]]. | + | *All these bursts have a uniform length of $156.25$ bit durations. This is discussed in more detail in the [[Aufgaben:Exercise_3.2:_GSM Data Rates|"Excercise 3.2"]]. |
== Modulation method for GSM== | == Modulation method for GSM== | ||
<br> | <br> | ||
| − | With GSM, only a bandwidth of $B = 200 \ \rm kHz$ is available per frequency channel, in which a total data rate (for eight users) of $R_{\rm | + | With GSM, only a bandwidth of $B = 200 \ \rm kHz$ is available per frequency channel, in which a total data rate (for eight users) of $R_{\rm total} = 270.833 \ \rm kbit/s$ must be transmitted. Required is therefore a modulation method with a bandwidth efficiency of at least |
| − | ::<math>\beta \ge {R_{\rm | + | ::<math>\beta \ge {R_{\rm total}}/{B} \approx 1.35 \,\,{\rm bit/s/Hz}.</math> |
| − | GSM uses the very bandwidth-efficient modulation method [[ | + | GSM uses the very bandwidth-efficient modulation method [[Examples_of_Communication_Systems/Radio_Interface#Gaussian_Minimum_Shift_Keying_.28GMSK.29| $\text{Gaussian Minimum Shift Keying}$]] $\rm (GMSK)$. It should again be expressly mentioned that this modulation method, just like the FDMA/TDMA multiple access, is exclusively based on the air interface between the mobile station $\rm (MS)$ and the base transceiver station $\rm (BTS)$, which is highlighted in yellow in the [[Mobile_Communications/Characteristics_of_GSM#System_architecture_and_basic_units_of_GSM|$\text{system architecture graphic}$]] at the beginning of the chapter. <br> |
| − | GMSK has already been described in chapter [[Modulation_Methods/ | + | GMSK has already been described in chapter [[Modulation_Methods/Non-Linear_Digital_Modulation#Properties_of_non-linear_modulation_methods| "Properties of nonlinear modulation methods"]] of the book "Modulation Methods". The most important properties are briefly summarized here. |
| − | *GMSK is a special form of binary [[Modulation_Methods/ | + | *GMSK is a special form of binary [[Modulation_Methods/Non-Linear_Digital_Modulation#FSK_.E2.80.93_Frequency_Shift_Keying| $\text{Frequency Shift Keying}$]] $\rm (FSK)$. A prerequisite for the orthogonality between the two waveforms is that the modulation index $h$ is a multiple of $0.5$ . For integer values of $h$ the demodulation can also be performed non-coherently.<br> |
| − | *For GSM you use the smallest possible modulation index $h = 0.5$. A higher value would require a much larger bandwidth. Such an FSK with $h = 0.5$ is also called [[Modulation_Methods/ | + | *For GSM you use the smallest possible modulation index $h = 0.5$. A higher value would require a much larger bandwidth. Such an FSK with $h = 0.5$ is also called [[Modulation_Methods/Non-Linear_Digital_Modulation#MSK_.E2.80.93_Minimum_Shift_Keying|$\text{Minimum Shift Keying}$]] $\rm (MSK)$. However, a coherent demodulation is then required.<br> |
| − | *A very narrow spectrum, however, is only obtained if the phase values at the symbol boundaries are matched to each other, thus avoiding phase jumps, which is given with MSK. Such methods are referred to as [[Modulation_Methods/ | + | *A very narrow spectrum, however, is only obtained if the phase values at the symbol boundaries are matched to each other, thus avoiding phase jumps, which is given with MSK. Such methods are referred to as [[Modulation_Methods/Nonlinear_Digital_Modulation#General_Description_of_Continuous_Phase_Modulation|$\text{Continuous Phase Frequency Shift Keying}$]] $\rm (CP–FSK)$. <br> |
| − | *For GSM, a low-pass filter with | + | *For GSM, a low-pass filter with Gaussian characteristic is inserted before the frequency modulator ⇒ [[Modulation_Methods/Nonlinear_Digital_Modulation#GMSK_.E2.80.93_Gaussian_Minimum_Shift_Keying|$\text{Gaussian Minimum Shift Keying}$]] $\rm (GMSK)$, which further reduces the bandwidth and improves bandwidth efficiency.<br><br> |
| − | Regarding the topic treated here (coherent or non-coherent demodulation of FSK) we refer to two | + | Regarding the topic treated here (coherent or non-coherent demodulation of FSK) we refer to two exercises in the book "Digital Signal Transmission": |
*[[Aufgaben:Aufgabe_4.16:_Binary_Frequency_Shift_Keying|Excercise 4.16: Binary Frequency Shift Keying]],<br> | *[[Aufgaben:Aufgabe_4.16:_Binary_Frequency_Shift_Keying|Excercise 4.16: Binary Frequency Shift Keying]],<br> | ||
| + | |||
*[[Aufgaben:Aufgabe_4.18Z:_BER_von_kohärenter_und_nichtkohärenter_FSK| Excercise 4.18Z: BER of coherent and non-coherent FSK]].<br><br> | *[[Aufgaben:Aufgabe_4.18Z:_BER_von_kohärenter_und_nichtkohärenter_FSK| Excercise 4.18Z: BER of coherent and non-coherent FSK]].<br><br> | ||
| + | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 1:}$ The following graphic is to clarify the previous statements: | $\text{Example 1:}$ The following graphic is to clarify the previous statements: | ||
| − | [[File:EN_Mob_T_3_3_S4.png|right|frame| | + | [[File:EN_Mob_T_3_3_S4.png|right|frame|Block diagram and signals with GMSK|class=fit]] |
| − | *Starting from a | + | *Starting from a Dirac shaped source signal $q_\delta(t)$ at point $(1)$ you pass through a filter with the rectangular impulse response $g_{\rm R}(t)$ to the rectangular signal $q_{\rm R}(t)$ at point $(2)$. |
| − | *If the Gaussian low-pass with the impulse response $h_{\rm G}(t)$ were to be omitted ⇒ $q_{\rm G}(t) = q_{\rm R}(t)$, a sectionwise linear phase function $\phi(t)$ would result at point $(4)$. All phase values would be multiples of $π/2$ at multiples of the symbol duration $T$ | + | *If the Gaussian low-pass with the impulse response $h_{\rm G}(t)$ were to be omitted ⇒ $q_{\rm G}(t) = q_{\rm R}(t)$, a sectionwise linear phase function $\phi(t)$ would result at point $(4)$. All phase values would be multiples of $π/2$ at multiples of the symbol duration $T$. |
| − | *After the phase modulator, a binary FSK | + | *After the phase modulator, a binary FSK signal $s(t)$ would appear at point $(5)$ with only two frequencies. This signal is at the same time a MSK signal due to the minimum modulation index $h = 0.5$ in case of orthogonality. |
| − | *Through the Gaussian low-pass $H_{\rm G}(f)$ with the cutoff frequency $f_{\rm G}= 0.45/T$ (valid for GSM) the frequency | + | *Through the Gaussian low-pass $H_{\rm G}(f)$ with the cutoff frequency $f_{\rm G}= 0.45/T$ (valid for GSM) the frequency impulse $g(t)$ is no longer rectangular but corresponds to the rectangular response of $H_{\rm G}(f)$. According to the Fourier transform, $g(t) = g_{\rm R}(t) \star h_{\rm G}(t)$ applies. |
| − | *Thus, the phase function $\phi(t)$ is no longer linear in sections but the corners are rounded, as can be seen from the phase function at point $(4)$. The violet–dotted curve applies to the data sequence assumed at point $(1)$. | + | *Thus, the phase function $\phi(t)$ is no longer linear in sections but the corners are rounded, as can be seen from the phase function at point $(4)$. The violet–dotted curve applies to the data sequence assumed at point $(1)$. |
| − | *The signal $s(t)$ at point $(5)$ of the block diagram is the GMSK | + | *The signal $s(t)$ at point $(5)$ of the block diagram is the GMSK signal. |
| − | Note: The GMSK | + | Note: The GMSK signal contains much more than just two discrete frequencies. Its power-spectral density decreases very fast, see [[Examples_of_Communication_Systems/Radio_Interface#Advantages_and_disadvantages_of_GMSK|$\text{diagram}$]] in the book "Examples of communication systems". From the above time representation at point $(5)$ of the block diagram this fact is difficult to recognize. |
<br clear=all>}} | <br clear=all>}} | ||
| − | == GSM | + | == GSM extensions == |
<br> | <br> | ||
| − | GSM was designed and developed as a European mobile radio system for telephone calls with the additional option of data transmission, but only at a low data rate $(9.6 \ \rm kbit/s)$. The standardization of the | + | GSM was designed and developed as a European mobile radio system for telephone calls with the additional option of data transmission, but only at a low data rate $(9.6 \ \rm kbit/s)$. The standardization of the $\text{GSM-Phase 2}$ however, from 1995 on, already included first further developments and some new additional services, already known from ISDN and appreciated by the users.<br> |
| − | In the years from 1997 to 2000 new data services with higher bit rates were developed, which are attributed to the | + | In the years from 1997 to 2000 new data services with higher bit rates were developed, which are attributed to the $\text{GSM-Phase 2+}$ $($or $\text{GSM-Phase 2.5)}$: |
| − | *[[Examples_of_Communication_Systems/Weiterentwicklungen_des_GSM#High_Speed_Circuit.E2.80.93Switched_Data_.28HSCSD.29| | + | *[[Examples_of_Communication_Systems/Weiterentwicklungen_des_GSM#High_Speed_Circuit.E2.80.93Switched_Data_.28HSCSD.29| $\text{High–Speed Circuit–Switched Data}$]] $\rm (HSCSD)$ offers a line-oriented transmission with $14.4 \ \rm kbit/s$ $($against $9.6 \ \rm kbit/s)$, if the channel is sufficiently good due to a higher code rate (dotting of the convolutional code). It also enables channel bundling by combining several time slots ⇒ "Multislot Capability". With a bundling of four time slots, this results in a maximum transmission rate of $57.6 \ \rm kbit/s$.<br> |
| − | *[[Examples_of_Communication_Systems/Weiterentwicklungen_des_GSM#General_Packet_Radio_Service_.28GPRS.29| | + | *[[Examples_of_Communication_Systems/Weiterentwicklungen_des_GSM#General_Packet_Radio_Service_.28GPRS.29|$\text{General Packet Radio Service}$]] $\rm (GPRS)$ enables communication with other networks such as the Internet or company intranets. It is packet-oriented (instead of line-oriented) and supports many data transfer protocols, for example the Internet Protocol (IP), X.25 and Datex–P. The charges for GPRS are not based on the connection duration, but on the amount of data transmitted. A GPRS user benefits from the shorter access times and the higher data rate up to $21.4 \ \rm kbit/s$. By the bundling of six time slots one reaches so maximally $128.4 \ \rm kbit/s$.<br> |
| − | *[[Examples_of_Communication_Systems/Weiterentwicklungen_des_GSM#Enhanced_Data_Rates_for_GSM_Evolution| | + | *[[Examples_of_Communication_Systems/Weiterentwicklungen_des_GSM#Enhanced_Data_Rates_for_GSM_Evolution|$\text{Enhanced Data Rates for GSM Evolution}$]] $\rm (EDGE)$ used in addition to GSM standard "GMSK" as a further modulation method [[Modulation_Methods/Quadrature_Amplitude_Modulation#Other_signal_space_constellations|$\text{8-PSK}$]], so that with each symbol three data bits are transmitted and in this way the data rate can (theoretically) be tripled. <br><br> |
| − | With the combination of GPRS and EDGE – one speaks then of | + | With the combination of GPRS and EDGE – one speaks then of $\text{E-GPRS}$ – there are nine different [[Examples_of_Communication_Systems/Weiterentwicklungen_des_GSM#Enhanced_Data_Rates_for_GSM_Evolution|$\text{Modulation and Coding Schemes}$]] $\rm (MCS)$, between which the operator can choose: |
| − | *with GMSK | + | *with GMSK or with 8–PSK modulation,<br> |
| − | *resulting code rates between $0.37$ and $1$, and<br> | + | *resulting code rates between $0.37$ and $1.00$, and<br> |
| − | * | + | *data rates between $8.8 \ \rm kbit/s$ (for MCS–1) and $59.2 \ \ \rm kbit/s$ (for MCS–9).<br><br> |
| − | In practice, however, MCS–8 $(54.4 \ \rm kbit/s)$ and seven time slots are the maximum applicable. With this, one reaches $380.8 \ \rm kbit/s$ and thus the order of magnitude of UMTS $(384 \ \rm kbit/s)$.<br> | + | In practice, however, MCS–8 $(54.4 \ \rm kbit/s)$ and seven time slots are the maximum applicable. With this, one reaches $380.8 \ \rm kbit/s$ and thus the order of magnitude of UMTS $(384 \ \rm kbit/s)$.<br> |
| − | We should also mention the [[Mobile_Communications/ | + | We should also mention the [[Mobile_Communications/General_Information_on_the_LTE_Mobile_Communications_Standard#Development_of_the_UMTS_mobile_phone_standards_towards_LTE|$\text{EDGE Evolution}$]] or "Evolved EDGE", i.e. the further development of the evolution of GSM in Release 7 (December 2007). For this, the developers specify data rates up to $1 \ \rm Mbit/s$ and halved latency times $(10 \ \rm ms$ instead of $20 \ \rm ms)$ . These values can be achieved among other things |
*by 32–QAM or 16–QAM Modulation instead of 8–PSK, | *by 32–QAM or 16–QAM Modulation instead of 8–PSK, | ||
| − | * an improved error correction through the use of [[Channel_Coding/Grundlegendes_zu_den_Turbocodes| | + | * an improved error correction through the use of [[Channel_Coding/Grundlegendes_zu_den_Turbocodes| $\text{Turbo codes}$]], and |
* an increase of the symbol rate of $20\%$ from $270.833 \ \rm ksymbol/s$ to $325\ \rm ksymbol/s$.<br> | * an increase of the symbol rate of $20\%$ from $270.833 \ \rm ksymbol/s$ to $325\ \rm ksymbol/s$.<br> | ||
| − | ==Exercises | + | ==Exercises for the chapter== |
<br> | <br> | ||
[[Aufgaben:Exercise 3.5: GMSK Modulation]] | [[Aufgaben:Exercise 3.5: GMSK Modulation]] | ||
Latest revision as of 17:41, 20 February 2023
Contents
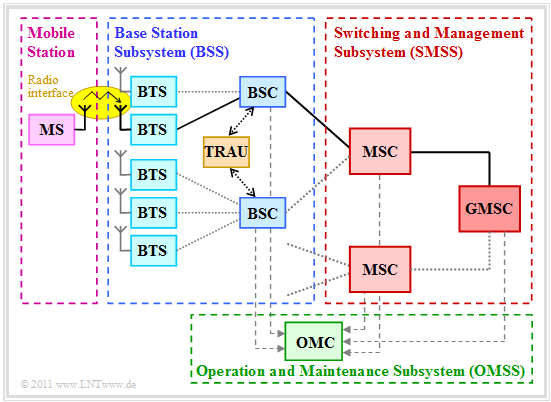
System architecture and basic units of GSM
$\rm GSM$ $\rm (G$lobal $\rm S$ystem for $\rm M$obile Communication$)$ is a strongly hierarchically structured system of different network components. You can see from the graphic:
- The mobile station $\rm (MS)$ communicates via the radio interface with the nearest base transceiver station $\rm (BTS$, transmit and receive base station).
- Several such BTS's are grouped together area by area and are jointly subordinate to a base station controller $\rm (BSC$, control station$)$.
- The base station sub–system $\rm(BSS)$ consists of a multitude of BTS's and several BSC's. In the graphic such a BSS is framed in blue.
- Each BSC is connected to a mobile switching center $\rm (MSC$, switching computer$)$, whose function is comparable to a switching node in the fixed network.
- The gateway mobile switching center $\rm (GMSC)$ is responsible for the connection between the fixed and mobile networks. For example, if a mobile subscriber is called from the fixed network, the GMSC determines the responsible MSC and transfers the call.
- The operation and maintenance center $\rm (OMC)$ monitors a part of the mobile network. It also takes on organizational tasks such as traffic flow control, charging, security management, etc.
More detailed information on GSM system architecture and the individual network components can be found in the chapter "General Description of GSM" of the book "Examples of Communication Systems".
Multiple access with GSM
GSM uses two multiple access methods in parallel:
- $\text{Frequency Division Multiple Access}$ $\rm (FDMA)$,
- $\text{Time Division Multiple Access}$ $\rm (TDMA)$.
The graphic and the following description is valid for the original system "GSM 900" (in the following: "GSM–D").
For "GSM/DCS 1800" ⇒ "GSM–E" comparable statements apply.
- With "GSM–D", a bandwidth of $25\ \rm MHz$ is provided for uplink and downlink respectively $($duplex spacing: $45\ \rm MHz)$. This is called "Frequency Division Duplex" $\rm (FDD)$. For "GSM–E", the bandwidth is $75\ \rm MHz$ and the duplex spacing is $95\ \rm MHz$.
- Uplink and downlink bands are divided into frequency bands of width $200\ \rm kHz$. Taking into account the protection areas at the respective edges, there are $N_{\rm F} = 124$ (GSM–D) or $N_{\rm F} = 374$ (GSM–E) frequency channels.
- Each cell is assigned a subset of the frequencies ⇒ "Cell Allocation". Neighboring cells usually work at different frequencies, for example with the reuse–factor $3$, as in section "Cellular architecture" indicated by the colors white, yellow, and blue.
- The $124$ GSM frequency channels are further divided by time division multiplexing $\rm (TDMA)$. Each FDMA channel is divided into TDMA frames, which each comprise $N_{\rm T} = 8$ time slots.
- The slots are periodically assigned to the individual GSM users and each contain a so-called $\text{Burst}$. Each user has a time slot available in each TDMA frame. A bundling (maximum six per user) is only possible with GPRS/EDGE.
- The TDMA frames of the uplink are sent delayed by three slots compared to the downlink: "Time Division Duplex" $\rm (TDD)$. The hardware of the mobile station can thus be used for sending and receiving a message simultaneously.
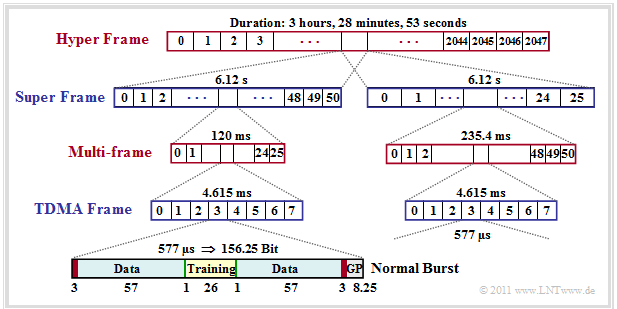
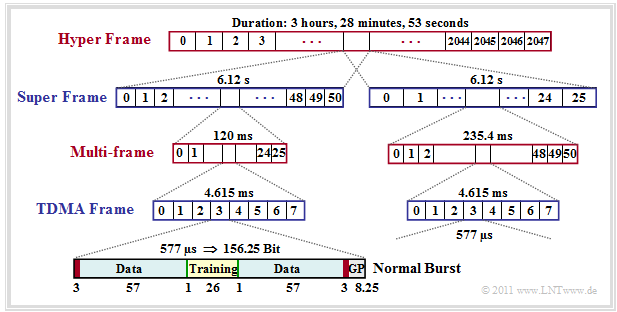
Data and frame structure for GSM
The mapping of logical to physical channels is done using the GSM frame structure. Here we only look to traffic channels and to the mapping in time. In this case, each multi–frame of $120 \ \rm ms$ duration is divided into $26$ TDMA frames (two of them for control channels) of $4.615\ \rm ms$ duration. Thus, the duration of a time slot is approximately $T_{\rm Z} = 576.9\ \rm µ s$.
You can see from this graphic:
- In each time slot one "burst" is transmitted, whose duration corresponds to $156.25$ bits. The bit duration is $T_{\rm B} = 576.9\ \rm µ s/156.25 \approx 3.692 \ \rm µs$ and for the total gross data rate:
- \[R_{\rm total} = {1}/{T_{\rm B}}= 270.833\,{\rm kbit/s}\hspace{0.05cm}.\]
- The »gross data rate« of each user is $R_{\rm gross} = 33.854 \ \rm kbit/s$. But since in every normal burst only $2 · 57 = 114$ data bits (highlighted blue in the graphic) are transmitted, it results in the lower »net data rate« $R_{\rm net} = 22.8 \ \rm kbit/s$.
- This net data rate also takes the channel coding into account. In the case of a speech signal, for every $20\ \rm kbit/s$ speech frame $456$ bits are transmitted, which results in exactly the rate $R_{\rm net} = 22.8 \ \rm kbit/s$. Without channel coding, the data rate would be only $13 \ \rm kbit/s$.
- In addition to the traffic data, a »normal burst« also contains
- – twice three tailbits (red, during this time the channel is remeasured),
- – two signaling bits (green),
- – the "Guard Period" $\rm (GP)$ with $8.25$ bit duration $($grey, ca. $30.5 \ \rm µ s)$,
- – $26$ bit for a training sequence (for channel estimation and synchronization).
These bits increase the data rate from $22.8$ to $33.854 \ \rm kbit/s$.
Note:
- In GSM, besides the "Normal Burst" there are some other $\text{types of bursts}$: Frequency Correction Burst, Synchronization Burst, Dummy Burst, Access Burst, ... .
- All these bursts have a uniform length of $156.25$ bit durations. This is discussed in more detail in the "Excercise 3.2".
Modulation method for GSM
With GSM, only a bandwidth of $B = 200 \ \rm kHz$ is available per frequency channel, in which a total data rate (for eight users) of $R_{\rm total} = 270.833 \ \rm kbit/s$ must be transmitted. Required is therefore a modulation method with a bandwidth efficiency of at least
- \[\beta \ge {R_{\rm total}}/{B} \approx 1.35 \,\,{\rm bit/s/Hz}.\]
GSM uses the very bandwidth-efficient modulation method $\text{Gaussian Minimum Shift Keying}$ $\rm (GMSK)$. It should again be expressly mentioned that this modulation method, just like the FDMA/TDMA multiple access, is exclusively based on the air interface between the mobile station $\rm (MS)$ and the base transceiver station $\rm (BTS)$, which is highlighted in yellow in the $\text{system architecture graphic}$ at the beginning of the chapter.
GMSK has already been described in chapter "Properties of nonlinear modulation methods" of the book "Modulation Methods". The most important properties are briefly summarized here.
- GMSK is a special form of binary $\text{Frequency Shift Keying}$ $\rm (FSK)$. A prerequisite for the orthogonality between the two waveforms is that the modulation index $h$ is a multiple of $0.5$ . For integer values of $h$ the demodulation can also be performed non-coherently.
- For GSM you use the smallest possible modulation index $h = 0.5$. A higher value would require a much larger bandwidth. Such an FSK with $h = 0.5$ is also called $\text{Minimum Shift Keying}$ $\rm (MSK)$. However, a coherent demodulation is then required.
- A very narrow spectrum, however, is only obtained if the phase values at the symbol boundaries are matched to each other, thus avoiding phase jumps, which is given with MSK. Such methods are referred to as $\text{Continuous Phase Frequency Shift Keying}$ $\rm (CP–FSK)$.
- For GSM, a low-pass filter with Gaussian characteristic is inserted before the frequency modulator ⇒ $\text{Gaussian Minimum Shift Keying}$ $\rm (GMSK)$, which further reduces the bandwidth and improves bandwidth efficiency.
Regarding the topic treated here (coherent or non-coherent demodulation of FSK) we refer to two exercises in the book "Digital Signal Transmission":
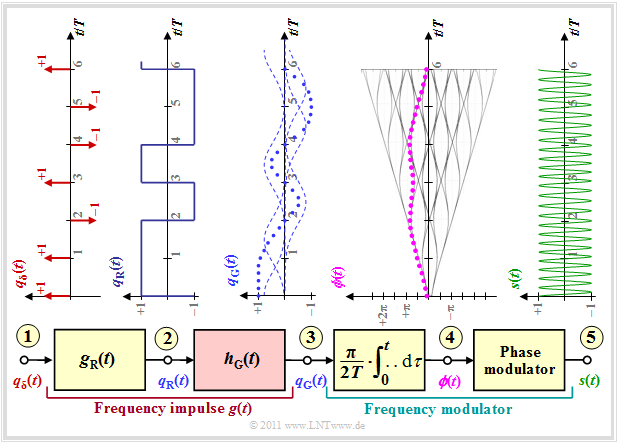
$\text{Example 1:}$ The following graphic is to clarify the previous statements:
- Starting from a Dirac shaped source signal $q_\delta(t)$ at point $(1)$ you pass through a filter with the rectangular impulse response $g_{\rm R}(t)$ to the rectangular signal $q_{\rm R}(t)$ at point $(2)$.
- If the Gaussian low-pass with the impulse response $h_{\rm G}(t)$ were to be omitted ⇒ $q_{\rm G}(t) = q_{\rm R}(t)$, a sectionwise linear phase function $\phi(t)$ would result at point $(4)$. All phase values would be multiples of $π/2$ at multiples of the symbol duration $T$.
- After the phase modulator, a binary FSK signal $s(t)$ would appear at point $(5)$ with only two frequencies. This signal is at the same time a MSK signal due to the minimum modulation index $h = 0.5$ in case of orthogonality.
- Through the Gaussian low-pass $H_{\rm G}(f)$ with the cutoff frequency $f_{\rm G}= 0.45/T$ (valid for GSM) the frequency impulse $g(t)$ is no longer rectangular but corresponds to the rectangular response of $H_{\rm G}(f)$. According to the Fourier transform, $g(t) = g_{\rm R}(t) \star h_{\rm G}(t)$ applies.
- Thus, the phase function $\phi(t)$ is no longer linear in sections but the corners are rounded, as can be seen from the phase function at point $(4)$. The violet–dotted curve applies to the data sequence assumed at point $(1)$.
- The signal $s(t)$ at point $(5)$ of the block diagram is the GMSK signal.
Note: The GMSK signal contains much more than just two discrete frequencies. Its power-spectral density decreases very fast, see $\text{diagram}$ in the book "Examples of communication systems". From the above time representation at point $(5)$ of the block diagram this fact is difficult to recognize.
GSM extensions
GSM was designed and developed as a European mobile radio system for telephone calls with the additional option of data transmission, but only at a low data rate $(9.6 \ \rm kbit/s)$. The standardization of the $\text{GSM-Phase 2}$ however, from 1995 on, already included first further developments and some new additional services, already known from ISDN and appreciated by the users.
In the years from 1997 to 2000 new data services with higher bit rates were developed, which are attributed to the $\text{GSM-Phase 2+}$ $($or $\text{GSM-Phase 2.5)}$:
- $\text{High–Speed Circuit–Switched Data}$ $\rm (HSCSD)$ offers a line-oriented transmission with $14.4 \ \rm kbit/s$ $($against $9.6 \ \rm kbit/s)$, if the channel is sufficiently good due to a higher code rate (dotting of the convolutional code). It also enables channel bundling by combining several time slots ⇒ "Multislot Capability". With a bundling of four time slots, this results in a maximum transmission rate of $57.6 \ \rm kbit/s$.
- $\text{General Packet Radio Service}$ $\rm (GPRS)$ enables communication with other networks such as the Internet or company intranets. It is packet-oriented (instead of line-oriented) and supports many data transfer protocols, for example the Internet Protocol (IP), X.25 and Datex–P. The charges for GPRS are not based on the connection duration, but on the amount of data transmitted. A GPRS user benefits from the shorter access times and the higher data rate up to $21.4 \ \rm kbit/s$. By the bundling of six time slots one reaches so maximally $128.4 \ \rm kbit/s$.
- $\text{Enhanced Data Rates for GSM Evolution}$ $\rm (EDGE)$ used in addition to GSM standard "GMSK" as a further modulation method $\text{8-PSK}$, so that with each symbol three data bits are transmitted and in this way the data rate can (theoretically) be tripled.
With the combination of GPRS and EDGE – one speaks then of $\text{E-GPRS}$ – there are nine different $\text{Modulation and Coding Schemes}$ $\rm (MCS)$, between which the operator can choose:
- with GMSK or with 8–PSK modulation,
- resulting code rates between $0.37$ and $1.00$, and
- data rates between $8.8 \ \rm kbit/s$ (for MCS–1) and $59.2 \ \ \rm kbit/s$ (for MCS–9).
In practice, however, MCS–8 $(54.4 \ \rm kbit/s)$ and seven time slots are the maximum applicable. With this, one reaches $380.8 \ \rm kbit/s$ and thus the order of magnitude of UMTS $(384 \ \rm kbit/s)$.
We should also mention the $\text{EDGE Evolution}$ or "Evolved EDGE", i.e. the further development of the evolution of GSM in Release 7 (December 2007). For this, the developers specify data rates up to $1 \ \rm Mbit/s$ and halved latency times $(10 \ \rm ms$ instead of $20 \ \rm ms)$ . These values can be achieved among other things
- by 32–QAM or 16–QAM Modulation instead of 8–PSK,
- an improved error correction through the use of $\text{Turbo codes}$, and
- an increase of the symbol rate of $20\%$ from $270.833 \ \rm ksymbol/s$ to $325\ \rm ksymbol/s$.
Exercises for the chapter
Exercise 3.5Z: GSM Network Components