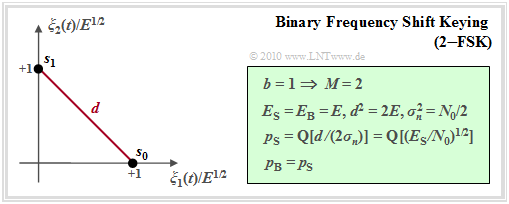Carrier Frequency Systems with Coherent Demodulation

1. Digital Signal Transmission
2. Generalized Description of Digital Modulation Methods
3. Carrier Frequency Systems with Coherent Demodulation

• Previous page
• Next page

• Previous page
• Next page

Signal space representation of linear modulation

In the first three chapters of this  fourth main chapter:   "Generalized Description of Digital Modulation Methods",  the structure of the optimal receiver and the signal representation by means of basis functions were treated by the example of baseband transmission.

Equivalent low-pass model of carrier-modulated transmission methods

With the same systematics and the same uniformity,  band–pass systems will now also be considered which have already been described in earlier books or chapters,  namely

• in the main chapter 4:  "Digital Modulation Methods"  of the book  "Modulation Methods",
  

• in the chapter  "Linear Digital Modulation - Coherent Demodulation"  of the present book.
  
  

In the following,  we restrict ourselves to  linear modulation methods  and  coherent demodulation.  This means that  "the receiver must know exactly the frequency and phase of the carrier signal added to the transmitter". 

In the following chapter  "Carrier Frequency Systems with Non-Coherent Demodulation"  are discussed.

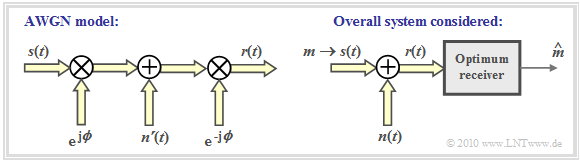
In the case of coherent demodulation,  the entire transmission system can be described in the  "equivalent low-pass domain",  and the relationship to baseband transmission is even more obvious than when band-pass signals are considered.

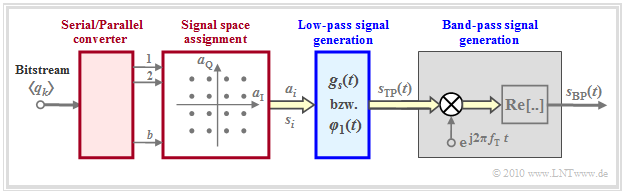
This results in the sketched model.  Complex quantities are marked by a yellow filled double arrow.  It should be noted with regard to this graph:

• From the incoming bit stream  $\langle q_k \rangle \in \{\rm 0, \ L \}$,    $b$  data bits each are converted serially/parallel.  These output bits result in the message  $m \in \{m_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, m_{M-1} \}$,  where  $M = 2^b$  indicates the level number.  For the following,  the message  $m = m_i$  is assumed.
  

• In the  signal space allocation,   a complex amplitude coefficient  $a_i = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i}$  is assigned to each message  $m_i$,  whose real part will form the  "in-phase component"  and whose imaginary part will form the  "quadrature component"  of the later transmitted signal.
  

• At the output of the blue marked block   generation of the low-pass signal   the (in general) complex-valued  "equivalent low-pass signal"  is present,  where  $g_s(t)$  shall be limited for the time being to the range  $ 0 \le t \le T$  just like  $s_{\rm TP}(t)$.  The index  $i$  again provides an indication of the message  $m_i$ sent:

\[s_{\rm TP}(t) \big {|}_{m \hspace{0.05cm}= \hspace{0.05cm} m_i} = a_i \cdot g_s(t) = a_{{\rm I}i} \cdot g_s(t) + {\rm j} \cdot a_{{\rm Q}i} \cdot g_s(t)\]

• By energy normalization one gets from the basic transmission pulse  $g_s(t)$  to the basis function

$$\varphi_1(t) = { g_s(t)}/{\sqrt{E_{gs}}} \hspace{0.4cm} {\rm with} \hspace{0.4cm} E_{gs} = \int_{0}^{T} g_s(t)^2 \,{\rm d} t$$

$$ \hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm TP}(t) \big {|}_{m\hspace{0.05cm} =\hspace{0.05cm} m_i} = s_{{\rm I}i} \cdot \varphi_1(t) + s_{{\rm Q}i} \cdot {\rm j} \cdot \varphi_1(t) \hspace{0.05cm}.$$

• While the coefficients   $a_{{\rm I}i}$   and   $a_{{\rm Q}i}$   are dimensionless,  the new coefficients   $s_{{\rm I}i}$   and   $s_{{\rm Q}i}$   have the unit  "root of energy"   ⇒   see page  "Nomenclature in the fourth main chapter":

$$s_{{\rm I}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm I}i}\hspace{0.05cm}, $$

$$ s_{{\rm Q}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm Q}i}\hspace{0.05cm}. $$

• The equations show that the system considered here is completely described in the equivalent low-pass  $($German:  "Tiefpass"   ⇒   "TP"$)$  domain by one real basis function  $\varphi_1(t)$  and one purely imaginary basis function  $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$  each,  or by a single complex basis function  $\xi_1(t)$. 
  

• The gray shaded part shows the model for generating the band-pass signal  $s_{\rm BP}(t)$,  first the generation of the  "analytical signal"  $s_{\rm +}(t) = s_{\rm TP}(t) \cdot {\rm e}^{{\rm j}2\pi \cdot f_{\rm T} \cdot T}$  and then the real part formation.
  

• The two basis functions of the band-pass signal  $s_{\rm BP}(t)$  result here as energy-normalized and time-limited to the range   $0 \le t \le T$   cosine and minus-sine oscillations, respectively.
  
  

Coherent demodulation and optimal receiver

In the following,  we always assume the equivalent low-pass signal unless explicitly stated otherwise.  In particular,  the signals 

AWGN channel model for complex signals KORREKTUR: optimal

• $s(t) = s_{\rm TP}(t)$  and 

• $r(t) = r_{\rm TP}(t)$ 

in the graph are  "low-pass signals"  and thus generally complex.  The suffix  "TP"  is omitted in the remainder of this paper KORREKTUR: in the following.

To this figure is to be noted:

• The phase delay of the channel  $($i.e. a phase function increasing linearly with frequency$)$  is expressed in the low-pass range by the time-independent rotation factor   ${\rm e}^{{\rm j}\hspace{0.05cm} \phi}$. 
  

• The signal  $n\hspace{0.05cm}'(t)$  describes a complex white Gaussian random process in the low-pass domain,  as given in the section  "N-dimensional Gaussian noise".  The apostrophe was added in order to be able to work with  $n(t)$  later in the overall system.
  

• The receiver knows the channel phase   $\phi$   and corrects it by the conjugate-complex rotation factor  ${\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$.  Thus,  the received signal in the equivalent low-pass range is:

\[r(t) = s(t) + n\hspace{0.05cm}'(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\phi}= s(t) + n(t) \hspace{0.05cm}.\]

• The phase rotation does not change the properties of the circular symmetric noise   ⇒   $n(t) = n\hspace{0.05cm}'(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\phi}$  has exactly the same statistical properties as  $n\hspace{0.05cm}'(t)$.  The left graphic in the figure above illustrates the facts just described.

1. The right graph shows the overall system as used for the rest of the fourth main chapter.
2. The AWGN channel is followed by an optimal receiver according to the section  "N-dimensional Gaussian noise".

$\text{Definition:}$  A  symbol error  occurs whenever  $\hat{m}$  does not match the sent message  $m$:

\[m = m_i \hspace{0.2cm} \cap \hspace{0.2cm} \hat{m} \ne m_i \hspace{0.05cm}.\]

On–off keying (2–ASK)

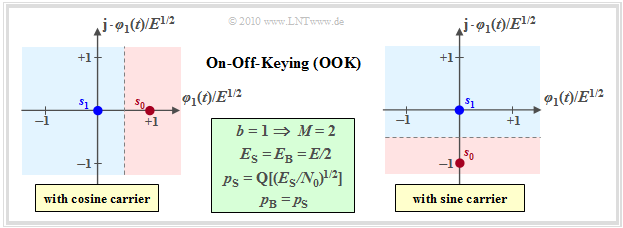
The simplest digital modulation method is  "On–off keying"  $\rm (OOK)$,  which has already been described in detail in the book  "Modulation Methods"  on the basis of its band-pass signals.  There,  this method was partly also called  "Amplitude Shift Keying"  $\rm (2–ASK)$.

Signal space constellations for on-off keying

This method can be characterized as follows:

• OOK is a one-dimensional modulation method  $(N = 1)$  with  $s_{{\rm I}i} = \{0, E^{1/2}\}$  and  $s_{{\rm Q}i} \equiv 0$  or  $s_{{\rm I}i} \equiv 0$  and  $s_{{\rm Q}i} = \{0, -E^{1/2}\}$.  As an abbreviation,  $E = E_{g_s}$.

• The first combination describes a cosinusoidal carrier signal,  the second combination a sinusoidal carrier.
  

• Each bit is assigned to a binary symbol  $(b = 1, \ M = 2)$; thus,  no serial/parallel converter is needed.

• For equally probable symbols,  which is assumed for what follows,  both the  "mean energy per symbol"  $(E_{\rm S})$  and the  "mean energy per bit"  $(E_{\rm B})$  are equal to  $E/2$.
  

• The optimal OOK receiver virtually projects the complex–valued received signal  $r(t)$  onto the basis function  $\varphi_1(t)$,  if one starts from the left sketch  (cosine carrier).
  

• Because of  $N = 1$,  the noise can be one-dimensional with the variance  $\sigma_n^2 = N_0/2$. 

• Using the statements in the section  "Error probability for symbols with equal probability",  we obtain for the (mean)  "symbol error probability":

\[p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{\frac{E}{2 N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.\]

• Since each bit is mapped to one symbol,  the average bit error probability  $p_{\rm B}$  is exactly:

\[p_{\rm B} = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.\]

Binary phase shift keying (BPSK)

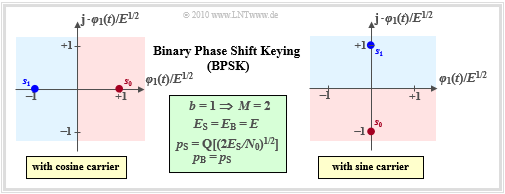
The very often used method  "Binary Phase Shift Keying"  $\rm (BPSK)$,  which was already described in detail in the chapter  "Linear Digital Modulation"  of the book "Modulation Methods"  using the band–pass signals  $($typical:   phase jumps$)$,  differs from  "On–off keying"  by a constant envelope.

For the signal space points,  $\boldsymbol{s}_1 = -\boldsymbol{s}_0$ always holds.  For example:

• with cosine carrier:   $s_{{\rm I}i} = \{\pm E^{1/2}\}$  and  $s_{{\rm Q}i} \equiv 0$, 
  

• with sinusoidal carrier:   $s_{{\rm I}i} \equiv 0$  and  $s_{{\rm Q}i} = \{\pm E^{1/2}\}$.

Signal space constellations of the BPSK

The improvements compared to on–off keying can be seen from the equations given in the graphic  $($in the field with green background$)$:

• For a given normalization energy  $E$,  the distance between  $\boldsymbol{s}_0$  and  $\boldsymbol{s}_1$  is twice as large as with OOK.

• This gives the error probability (both related to symbols and bits):

\[p_{\rm S} = p_{\rm B} = {\rm Pr}({\cal{E}}) = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{2 E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}.\]

• Now  $E_{\rm S} = E_{\rm B} = E$  applies,  which means that the average energies per symbol or per bit are now twice as large as with OOK.
  

• Because of factor  $2$  in the square root in Q-function's argument,  the BPSK error probability is noticeably lower than OOK with same   $E_{\rm S}$  and  $N_0$.
  

• In other words:   With the same  $N_0$,  BPSK only requires half the symbol energy  $E_{\rm S}$  in order to achieve the same error probability as OOK.  The logarithmic gain is  $3 \ \rm dB$.
  

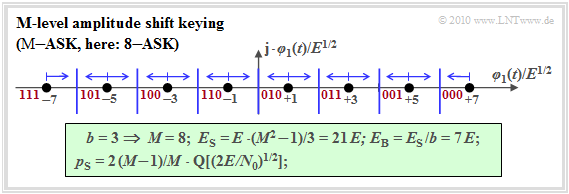
M–level amplitude shift keying (M–ASK)

In analogy to  "M–level baseband transmission",  we now consider  "M–level Amplitude Shift Keying"  $\text{(M–ASK)}$,  whose low-pass signal space constellation for the parameters  $b = 3$   ⇒   $M = 8$   ⇒   "$\text{8–ASK}$"  looks as follows.

The name  "M–ASK"  is not entirely accurate.  Rather,  it is a  "combined ASK/PSK method",  since e.g.

• the two innermost signal space points  $(\pm 1)$  do not differ in terms of amplitude  ("envelope"),
• but only in terms of phase  $(0^\circ$ or $180^\circ)$.

Signal room constellation of the 8-ASK

It should also be noted:

• The  "average energy per symbol"  can be calculated as follows for this one-dimensional modulation method using symmetry:

\[E_{\rm S} = \frac{2}{M} \cdot \sum_{k = 1}^{M/2} (2k -1)^2 \cdot E = \frac{M^2 -1}{3} \cdot E \hspace{0.05cm}.\]

• Since each of the  $M$  symbols represents  $b = \log_2 (M)$  bits,  the  "average energy per bit"  is:

$$E_{\rm B} = \frac{E_{\rm S}}{b} = \frac{E_{\rm S}}{{\rm log_2}\, (M)} =\frac{M^2 -1}{3 \cdot {\rm log_2}\, (M)} \cdot E$$

$$\Rightarrow\hspace{0.3cm}M= 8\hspace{-0.1cm}: \hspace{0.2cm} E_{\rm S}/E = 21 \hspace{0.05cm}, \hspace{0.2cm}E_{\rm B}/E = 7\hspace{0.05cm}.$$

• The probability that one of the two outer symbols is falsified due to AWGN noise is therefore the same:

\[{\rm Pr}({\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} \text{outer symbol)} = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right )\hspace{0.05cm}.\]

• The falsification probability of the  $M-2$  inner symbols is twice as large, since other decision regions border on both the right and the left.  By averaging one obtains for the  "symbol error probability":

\[p_{\rm S} = {\rm Pr}({\cal{E}}) = \frac{1}{M} \cdot \left [ 2 \cdot 1 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) + (M-2) \cdot 2 \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \right ] \]

\[\Rightarrow \hspace{0.3cm} p_{\rm S} = \frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) =\frac{2 \cdot (M-1)}{M} \cdot {\rm Q} \left ( \sqrt{\frac{6 \cdot E_{\rm S}}{(M^2-1) \cdot N_0}}\right ) \hspace{0.05cm}.\]

• When using the  "Gray code"  $($neighboring symbols each differ by one bit$)$,  the  "bit error probability"  $p_{\rm B}$ is approximately factor  $b = \log_2 \ (M)$  smaller than the  $p_{\rm S}$:

\[p_{\rm B} \approx \frac{p_{\rm S}}{b} = \frac{2 \cdot (M-1)}{M \cdot {\rm log_2}\, (M)} \cdot {\rm Q} \left ( \sqrt{{6 \cdot {\rm log_2}\, (M)}/({M^2-1 }) \cdot { E_{\rm B}}/{ N_0}}\right ) \hspace{0.05cm}.\]

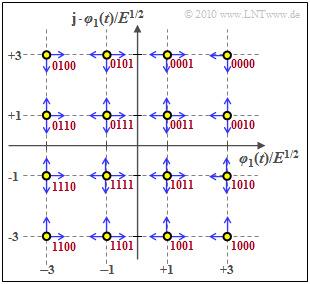
Quadrature amplitude modulation (M-QAM)

"Quadrature amplitude modulation"  $\text{(M–QAM)}$ results from a  M–ASK each for the  "in-phase component"  and the "quadrature component"  ⇒   $M^2$  signal space points.

Signal space constellation of 16-QAM

• Each symbol now represents  $b = \log_2 (M)$  binary characters  (bits).

• The graphic shows the special case  $M = 16$   ⇒   $b = 4$.

• The bit assignment for  "Gray coding"  is shown in red (neighboring symbols each differ by one bit).
  

The  "average energy per symbol"   $(E_{\rm S})$   or the  "average energy per bit"   $(E_{\rm B})$  can be easily derived from the result for the  "M–ASK"   $($note the difference in the equation between an energy  "$E$"  and the expected value  "$\rm E[\text{...}]$"$)$:

\[E_{\rm S} = {\rm E} \left [ |s_{i}|^2 \right ] = {\rm E} \left [ |s_{{\rm I}i}|^2 \right ] + {\rm E} \left [ |s_{{\rm Q}i}|^2 \right ] = 2 \cdot {\rm E} \left [ |s_{{\rm I}i}|^2 \right ]\]

\[\Rightarrow \hspace{0.3cm} E_{\rm S} = 2 \cdot \frac{M_{\rm I}^2-1}{3} \cdot E = \frac{2}{3} \cdot (M-1) \cdot E\hspace{0.01cm},\hspace{0.3cm}E_{\rm B} =\frac{2 \cdot (M-1)}{3 \cdot {\rm log_2}\, (M)} \cdot E \hspace{0.01cm}.\]

In addition,   the M–level quadrature amplitude modulation shows the following properties:

• The  "Union Bound"  can be used as an upper bound for the symbol error probability,  whereby it should be noted that an inner symbol can be falsified in four directions:

\[p_{\rm S} = {\rm Pr}({\cal{E}}) \le \left\{ \begin{array}{c} 4 \cdot p \\ 2 \cdot p \end{array} \right.\quad \begin{array}{*{1}c} {\rm for} \hspace{0.15cm} M \ge 16 \hspace{0.05cm}, \\ {\rm for} \hspace{0.15cm} M = 4 \hspace{0.05cm},\\ \end{array} \hspace{0.4cm} {\rm with} \hspace{0.4cm} p = {\rm Q} \left ( \sqrt{{2 E}/{N_0}}\right ) \hspace{0.05cm}.\]

• If one takes into account that only the  $(b-2)^2$  inner points are falsified in four directions,  in contrast,  the four vertices are falsified only in two and the remaining points in three directions  (blue arrows in the graphic),  therefore one obtains with  $M = b^2$  the better approximation

\[p_{\rm S} \approx {1}/{M} \cdot \big [(b - 2)^2 \cdot 4p + 4 \cdot 2p + 4 \cdot (b - 2) \cdot 3p \big ] = {p}/{M} \cdot \big [ 4 \cdot M - 16 \cdot \sqrt{M} + 16 + 8 + 12 \cdot \sqrt{M} - 24\big ] \]

\[\Rightarrow \hspace{0.3cm} p_{\rm S} \approx {4 \cdot p}/{M} \cdot \big [ M - \sqrt{M} \big ] = 4p \cdot \hspace{0.05cm} \big [ 1 - {1}/{\sqrt{M}} \hspace{0.05cm}\big ] \]

\[\Rightarrow\hspace{0.3cm} M = 16\hspace{-0.1cm}: \hspace{0.1cm} p_{\rm S} \approx 3 \cdot p = 3 \cdot {\rm Q} \big ( \sqrt{{2 E}/{N_0}}\big ) = 3 \cdot {\rm Q} \big ( \sqrt{{1/5 \cdot E_{\rm S}}/{ N_0}}\big ) \hspace{0.05cm}.\]

$\text{Conclusion:}$  With  $M$–level QAM,   $E_{\rm B} = E_{\rm S}/\log_2 \hspace{0.05cm} (M)$  generally applies and with Gray coding,  $p_{\rm B} = p_{\rm S}/\log_2 \hspace{0.05cm} (M)$ is also applicable.

• This gives the  mean bit error probability:

\[p_{\rm B} \approx \frac{4 \cdot (1 - 1/\sqrt{M})}{ {\rm log_2}\hspace{0.05cm} (M)} \cdot {\rm Q} \left ( \sqrt{ \frac{3 \cdot {\rm log_2}\, (M)}{M-1 } \cdot { E_{\rm B} }/{ N_0} }\right ) \hspace{0.05cm}.\]

• The approximation is exactly valid for  $M \le 16$  if  – as assumed for the upper graphic –  no  "diagonal falsifications"  occur.

• The special case  "4–QAM"  (without inner symbols)  is dealt with in  "Exercise 4.13". 
  

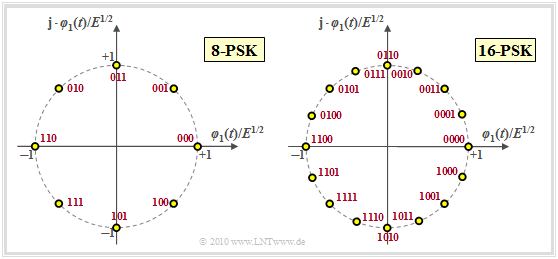
Multi-level phase–shift keying (M–PSK)

In the case of multi-level phase modulation,  in which case the level number  $M$  is usually a power of two in practice,  all signal space points are evenly distributed on a circle with radius  $E^{1/2}$.  This means that  

Signal space constellation of the 8–PSK and 16–PSK

1. $E_{\rm S} = E$  holds for the  "'average symbol energy",  and
2. $E_{\rm B} = E_{\rm S}/b = E/\hspace{-0.05cm}\log_2 \hspace{0.05cm} (M)$ for the  "average energy per bit". 
   

• For the in-phase and quadrature components of the signal space points  $\boldsymbol{s}_i$,  the general rule is  $(i = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, \hspace{0.05cm}M-1)$:

$$s_{{\rm I}i} = \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$

$$ s_{{\rm Q}i} = \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right )$$

$$\Rightarrow \hspace{0.2cm} || \boldsymbol{ s}_i || = \sqrt{ s_{{\rm I}i}^2 + s_{{\rm Q}i}^2} = 1 \hspace{0.05cm}.$$

• The phase offset is set to  $\phi_{\rm off} = 0$  in the graphic above. The 4–PSK with  $\phi_{\rm off} = \pi/4 \ (45^\circ)$  is identical to the  "4–QAM".

• The distance between two adjacent points is the same in all cases:
  

\[d_{\rm min} = d_{\rm 0, \hspace{0.05cm}1} = d_{\rm 1, \hspace{0.05cm}2} = \hspace{0.05cm}\text{...} \hspace{0.05cm} = d_{M-1, \hspace{0.05cm}0} = 2 \cdot \sqrt{E} \cdot \sin (\pi/M)\]

\[\Rightarrow\hspace{0.3cm} M = 4\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} = \sqrt{2} \approx 1.414 \hspace{0.05cm}, \hspace{0.8cm} M = 8\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.765 \hspace{0.05cm},\hspace{0.8cm} M = 16\hspace{-0.1cm}:\hspace{0.1cm}d_{\rm min}/E^{1/2} \approx 0.390 \hspace{0.05cm}.\]

• The upper bound  $p_{\rm UB}$  for the AWGN symbol error probability  $p_{\rm S}$  after the  "Union Bound"  yields:

\[p_{\rm UB} = 2 \cdot {\rm Q} \left ( \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right ) \ge p_{\rm S} \hspace{0.05cm}.\]

• One recognises:

1. For  $M = 2$  $\rm (BPSK)$  one obtains the estimate   $p_{\rm S} \le p_{\rm UB} =2 \cdot {\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$.  A comparison with the equation   $p_{\rm S} ={\rm Q} \left ( \sqrt{ 2E_{\rm S}/{ N_0} }\right )$   given on the  "BPSK section"  shows that in this special case the  "Union Bound"  returns double the value as the upper limit.
2. The larger  $M$  is,  the more precisely  $p_{\rm UB}$  approximates the exact symbol error probability  $p_{\rm S}$.  The interactive SWF applet  "Multi-level PSK & Union Bound"  also gives the more accurate error probability obtained through simulation.
   

$\text{Conclusion:}$  The limit for the  M–PSK bit error probability  is,  assuming Gray code  ⇒  red labeling:

\[p_{\rm B} \le \frac{2}{ {\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{ {\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.\]

• However,  this limit only has to be applied for  $M > 4$. 

• For  $M = 2$  (BPSK)  and  $M = 4$  (identity between 4–PSK and 4–QAM),  the bit error probability can be specified exactly:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ { {2E_{\rm B} } }/{ N_0} }\right ) \hspace{0.05cm}.$$

Binary frequency shift keying (2–FSK)

This type of modulation with parameter  $b = 1$   ⇒   $M = 2$   has already been described in detail in the section  "FSK – Frequency Shift Keying"  of the book  "Modulation Methods"  using the band-pass signals.

• The two possible signal forms are represented by two different frequencies in the range  $0 \le t \le T$: 
  

\[s_{\rm BP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} + \Delta f_{\rm A})\cdot t)\hspace{0.05cm},\]

\[ s_{\rm BP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} A \cdot \cos( 2\pi \cdot( f_{\rm T} - \Delta f_{\rm A})\cdot t)\hspace{0.05cm}.\]

• $f_{\rm T}$  designates the  "carrier frequency"  and  $\Delta f_{\rm A}$  the (one-sided)  "frequency deviation".  The average energy per symbol or per bit is the same in each case:

\[E_{\rm S} = E_{\rm B} = E = \frac{A^2 \cdot T}{2} \hspace{0.05cm}.\]

• The FSK in the equivalent low-pass signal space is now to be considered here.  Then:

\[s_{\rm TP0}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

\[ s_{\rm TP1}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

and for the  "inner product"  one obtains:

\[< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \hspace{-0.1cm} \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t = A^2 \cdot \int_{0}^{T} {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot t} \,{\rm d} t = \frac{A^2}{{\rm j} \cdot 4\pi \cdot \Delta f_{\rm A}} \cdot \big [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 4\pi \hspace{0.03cm}\cdot \hspace{0.03cm} \Delta f_{\rm A} \hspace{0.03cm}\cdot T} - 1 \big ] \hspace{0.05cm}.\]

$\text{Definition:}$  The  modulation index  $h = 2 \cdot \Delta f_{\rm A}\hspace{0.03cm}\cdot T$  is the ratio

• between the total (bilateral) frequency deviation  $(2 \cdot \Delta f_{\rm A})$ 

• and the symbol rate  $(1/T)$.

• The two signals are  "orthogonal"  if this inner product is equal to zero:

Signal space constellation of the FSK, if  $h$  is an integer

$$< \hspace{0.02cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{0.02cm}> \hspace{0.1cm} = \frac{A^2\cdot T}{{\rm j} \cdot 2\pi \cdot h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} 2h} - 1 \right ] = 0$$

$$ \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T = 1,\hspace{0.1cm} 2, \hspace{0.1cm}3,\ \text{ ... }\hspace{0.05cm}.$$

• If the modulation index  $h$  is assumed to be an integer, the low-pass signals can be written in the form

\[s_{\rm TP0}(t) = \sqrt{E} \cdot \xi_1(t) \hspace{0.05cm},\]

\[s_{\rm TP1}(t) = \sqrt{E} \cdot \xi_2(t)\]

with complex basis functions:

$$\xi_1(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

$$ \xi_2(t)= \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.$$

• The result is the signal space representation of the binary FSK outlined here.
  

$\text{Conclusions:}$ 

• With an integer modulation index  $h$,  the low-pass signals   $s_{\rm TP0}(t)$  and   $s_{\rm TP1}(t)$  of the binary FSK are orthogonal to one another.
  

• This results in the symbol error probability  (derivation in the graphic):

\[p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q} \left ( \sqrt{ { {E_{\rm S} } }/{ N_0} }\right ) \hspace{0.05cm}.\]

• The bit error probability has the same value:   $p_{\rm B} = p_{\rm S}$.

Note:

1. In contrast to the representation in  [KöZ08],  the frequency deviation  $\Delta f_{\rm A}$  is defined here on one side.
2. Therefore,  the equations sometimes differ by a factor of  $2$.  However,  if you work with the modulation index  $h$,  there are no differences.
   

Minimum Shift Keying (MSK)

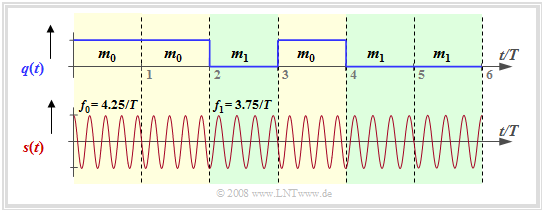
"Minimum Shift Keying"  $\rm (MSK)$  is a binary FSK system with the modulation index  $h = 0.5$   ⇒   frequency deviation $\Delta f_{\rm A} = 1/(2T)$. The graphic shows an MSK signal for the carrier frequency  $ f_{\rm T} = 4/T$:

Source signal and band-pass MSK signal

• The two frequencies within the transmitted signal are  $ f_{\rm 0} = f_{\rm T} + 1/(4T)$  to represent the message  $m_0$  (yellow background)  and  $ f_{\rm 1} = f_{\rm T} -1/(4T)$   ⇒   message  $m_1$  (green background).

• The graph also accounts for continuous phase adjustment at the transitions to further reduce the signal bandwidth.  This is then referred to as  "Continuous Phase Modulation"  $\rm (CPM)$.
  

Without this phase adjustment,  the two band-pass waveforms are:

\[s_{\rm BP0}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

\[ s_{\rm BP1}(t) = \sqrt{2E/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm}.\]

If you form the inner product of the band-pass signals,  you get with the abbreviation  $f_{\rm \Delta} = f_0 - f_1$  and  $f_{\rm \Sigma} = f_0 + f_1$:

\[< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {2E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_0 t) \cdot \cos( 2\pi f_1 t)\,{\rm d} t = {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Delta} t) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \cos( 2\pi f_{\rm \Sigma} t) \,{\rm d} t\]

\[ \Rightarrow \hspace{0.3cm}< \hspace{0.02cm} s_{\rm BP0}(t) \hspace{0.2cm} \cdot \hspace{0.2cm} s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm} = {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm} \cos( \pi \cdot {t}/{T}) \,{\rm d} t + {E}/{T} \cdot \int_{0}^{T} \hspace{-0.1cm}\cos( 2\pi \cdot 2 f_{\rm T} \cdot t) \,{\rm d} t \hspace{0.05cm}.\]

1. The first integral is zero  $($integral over  "cosine"  from  $0$  to  $\pi)$.
2. For  $f_{\rm T} \gg 1/T$,  which can be assumed in practice,  the second integral also vanishes.
3. This gives the inner product:     $< \hspace{0.02cm} s_{\rm BP0}(t) \cdot s_{\rm BP1}(t) \hspace{0.02cm}> \hspace{0.2cm}= 0 \hspace{0.05cm}.$

$\text{Conclusions:}$ 

(1)   This shows that the two band-pass signals are orthogonal for the modulation index  $h = 0.5$  $($i.e.  $\rm MSK)$  and all multiples thereof.

(2)   With the new real basis functions

\[\varphi_1(t) = \sqrt{2/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]

\[ \varphi_2(t) = \sqrt{2/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\]

one obtains exactly the same signal space constellation as for even-numbered   $h = 1, 2, 3, \ \text{ ...}$.

(3)   This results in the same  $($symbol resp. bit$)$  error probability:

\[p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q} \left ( \sqrt{ { {E_{\rm S} } }/{ N_0} }\right ) = p_{\rm B} \hspace{0.05cm}.\]

Exercises for the chapter

Exercise 4.11: On-Off Keying and Binary Phase Shift Keying

Exercise 4.11Z: OOK and BPSK once again

Exercise 4.12: Calculations for the 16-QAM

Exercise 4.13: Four-level QAM

Exercise 4.14: 8-PSK and 16-PSK

Exercise 4.14Z: 4-QAM and 4-PSK

Exercise 4.15: Optimal Signal Space Allocation

Exercise 4.16: Binary Frequency Shift Keying