Non-Linear Digital Modulation

1. Modulation Methods
2. Digital Modulation Methods
3. Non-Linear Digital Modulation

• Previous page
• Next page

• Previous page
• Next page

Properties of nonlinear modulation methods

All modulation methods can be alternatively classified as:

• amplitude, phase and frequency modulation,
• analog and digital modulation methods,
• linear and non-linear modulation methods.

Considering this last distinction, the following definition applies:

$\text{Definition:}$  A  linear modulation method  is present if any linear combination of signals at modulator input leads to a corresponding linear combination at its output. Otherwise, it is   non-linear modulation.

At the  beginning of the book  it was already pointed out that the main difference between an analog and a digital modulation method is that in the first one an analog source signal  $q(t)$  is present and in the second one a digital signal. However, a closer look will reveal that there are a few more differences between these methods. This will be discussed in more detail below.

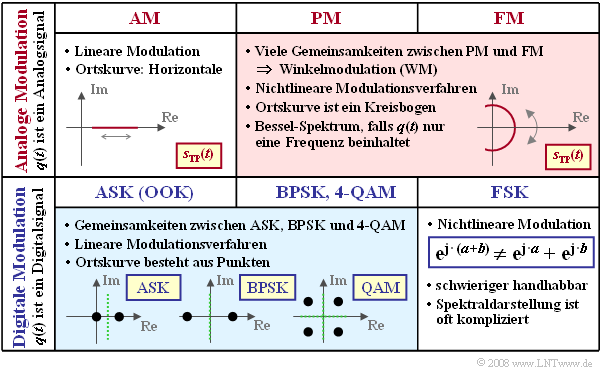
The following diagram shows some of the differences with respect to the classifications given above.

Analog and digital AM, PM and FM methods KORREKTUR

•  Analog amplitude modulation  $\rm (AM)$  is a linear method. The locus curve - that is, the equivalent low-pass signal  $s_{\rm TP}(t)$  represented in the complex plane - is a straight line.

• There are many similarities between  analog phase modulation  $\rm (PM)$  and  analog frequency modulation  $\rm (FM)$    ⇒ common description as angle modulation  $\rm (WM)$.  In that case, the locus curve is the arc of a circle. In harmonic oscillation, there is a line spectrum  $S(f)$  at multiples of the message frequency $f_{\rm N}$  around the carrier frequency  $f_{\rm T}$.

•  Digital amplitude modulation, referred to as either   Amplitude Shift Keying  $\rm (ASK)$  or as On–Off–Keying  $\rm (OOK)$ , is also linear. In the binary case, the locus curve consists of only two points.

• Since binary phase modulation $($Binary Phase Shift Keying,  $\rm BPSK)$ can be represented as  $\rm ASK$  with bipolar amplitude coefficients, it is also linear.  The shape of the BPSK power-spectral density is essentially determined by the magnitude square spectrum  $|G_s(f)|^2$  of the fundamental transmission pulse.

• However, this also means:  

1.   The BPSK spectral function is continuous in  $f$, unlike the analog phase modulation of a harmonic oscillation (which only has one frequency!).
2.   If one were to consider BPSK as (analog) phase modulation with digital source signal  $q(t)$ , then an infinite number of Bessel line spectra would have to be convolved together to calculate  ${\it Φ}_s(f)$  when  $Q(f)$  is represented as an infinite sum of individual frequencies.

• Since  quadrature amplitude modulation  with four signal space points   $\rm (4–QAM)$  can also be described as the sum of two mutually orthogonal, quasi-independent BPSK systems, it too represents a linear modulation scheme. The same applies to the  higher-level QAM methods  such as   $\rm 16–QAM$,   $\rm 64–QAM$, ...

• Higher-level   Phase Shift Keying, such as  $\rm 8–PSK$, is linear only in special cases, see [Klo01].  Digital frequency modulation  $($Frequency Shift Keying,  $\rm FSK)$  is always nonlinear. This method is described below, where we restrict our focus to the binary case  $\rm (2-FSK)$ .

FSK – Frequency Shift Keying

Now we assume

• the transmitted signal of the analog frequency modulation,

$$s(t) = s_0 \cdot \cos\hspace{-0.05cm}\big [\psi(t)\big ] \hspace{0.2cm} {\rm with} \hspace{0.2cm} \psi(t) = 2\pi f_{\rm T} \hspace{0.05cm}t + K_{\rm FM} \cdot \int q(t)\hspace{0.1cm} {\rm d}t,$$

• the rectangular binary signal with  $a_ν ∈ \{+1, –1\}$   ⇒   bipolar signaling:

$$q(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g_s (t - \nu \cdot T) \hspace{0.2cm} {\rm with} \hspace{0.2cm} g_s(t) = \left\{ \begin{array}{l} A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{ }} \\ \end{array}\begin{array}{*{10}c} 0 < t < T\hspace{0.05cm}, \\ {\rm otherwise} \hspace{0.05cm}. \\ \end{array}$$

Summarizing the amplitude  $A$  and the modulator constant  $K_{\rm FM}$  into the frequency deviation (see below for definition)

$${\rm \Delta}f_{\rm A} = \frac{A \cdot K_{\rm FM}}{2 \pi}$$

then the  FSK transmit signal  in the  $ν$–th time interval is:

$$s(t) = s_0 \cdot \cos\hspace{-0.05cm}\big [2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} ) \big ]\hspace{0.05cm}.$$

This can be calculated with the two possible signal frequencies

$$f_{\rm +1} = f_{\rm T} +{\rm \Delta}f_{\rm A} \hspace{0.05cm}, \hspace{0.2cm}f_{\rm -1} = f_{\rm T} -{\rm \Delta}f_{\rm A}$$

and written as:

$$s(t) = \left\{ \begin{array}{l} s_0 \cdot \cos (2 \pi \cdot f_{\rm +1} \cdot t ) \\ s_0 \cdot \cos (2 \pi \cdot f_{\rm -1} \cdot t ) \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{for}} \\ \end{array}\begin{array}{*{10}c} a_{ \nu} = +1 \hspace{0.05cm}, \\ a_{ \nu} = -1\hspace{0.05cm}. \\ \end{array}$$

• Thus, at any given time, only one of the two frequencies  $f_{+1}$  and  $f_{–1}$  arises. 
• The carrier frequency   $f_{\rm T}$  itself does not occur in the signal.

$\text{Definition:}$  The  frequency deviation  $Δf_{\rm A}$  is defined in the same way as for analog frequency modulation, namely as the maximum deviation of the instantaneous frequency  $f_{\rm A}(t)$  from the carrier frequency  $f_{\rm T}$. Sometimes the frequency deviation is also referred to as  $Δf$ or  $F$  in the literature.

Another important descriptive quantity in this context is the "modulation index", which was also already defined for analog frequency modulation as  $η = Δf_{\rm A}/f_{\rm N}$ .  For FSK, a slightly different definition is required, which is taken into account here with a different variable symbol:   $η   ⇒   h$.

$\text{Definition:}$  For digital frequency modulation (FSK), the  modulation index   $h$  denotes the ratio of the total frequency deviation and the symbol rate  $1/T$:

$$h = \frac{2 \cdot {\rm \Delta}f_{\rm A} }{1/T} = 2 \cdot {\rm \Delta}f_{\rm A}\cdot T \hspace{0.05cm}.$$

Sometimes  $h$  is also referred to as phase deviation in the literature.

Signal waveforms  $q(t)$,  $z(t)$  and  $s(t)$  for binary FSK

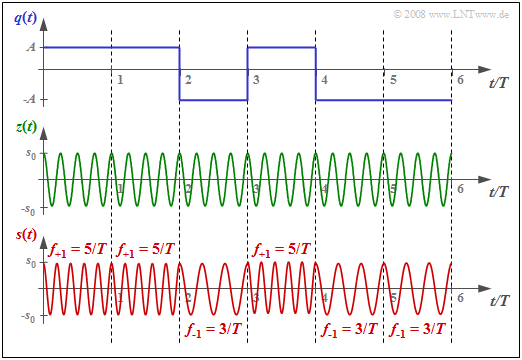
$\text{Example 1:}$  The graph below shows the FSK transmitted signal  $s(t)$  for

• the binary source signal  $q(t)$  sketched above with amplitude values  $\pm A =\pm 1 \ \rm V$, and
• the carrier signal  $z(t)$  drawn below with four oscillations per symbol duration  $(f_{\rm T} · T = 4)$.

The underlying frequency deviation is $Δf_{\rm A} = 1/T$   ⇒ modulation index  $h = 2$. The two possible frequencies are  $f_{\rm +1} = 5/T \hspace{0.05cm},\hspace{0.2cm}f_{\rm -1} = 3/T \hspace{0.05cm}.$

Thus, for an FSK transmission system with bit rate  $1 \ {\rm Mbit/s} \ \ (T = 1 \ \rm µ s)$ , the following FM constant would have to be used:

$$K_{\rm FM} = \frac{2 \pi \cdot {\rm \Delta}f_{\rm A} }{A } = \frac{2 \pi }{A \cdot T } \approx 6.28 \cdot 10^{6}\,\,{\rm V^{-1}s^{-1} }\hspace{0.05cm}.$$

Coherent demodulation of FSK

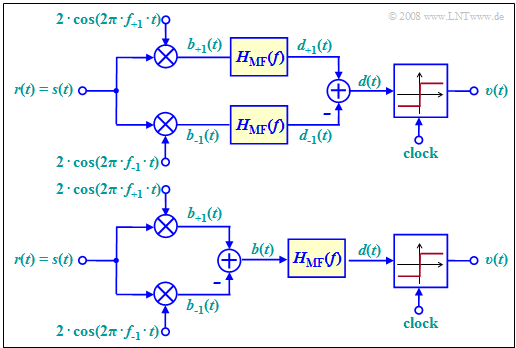
The diagram shows the best possible demodulator for binary FSK that operates coherently and thus requires knowledge of the phase of the FSK signal. This is accounted for in the block diagram by assuming that the received signal  $r(t)$  is equal to the transmitted signal  $s(t)$  - see signal waveforms in the previous section.

Coherent FSK demodulator

This demodulator operates according to the following principle (see upper arrangement):

• We are dealing with a  maximum–likelihood receiver  $\rm (ML)$  with a  Matched-Filter realization.  This filter with frequency response $H_{\rm MF}(f)$  can also be realized as an integrator with the assumed rectangular fundamental transmit pulse  $g_s(t)$ .
• Both signals  $b_{+1}(t)$  and  $b_{–1}(t)$  before their corresponding matched–filters ergeben are obtained by phase-appropriate multiplication with the oscillations of the frequencies  $f_{+1}$  and  $f_{–1}$, respectively.
• The maximum likelihood receiver is known to decide on the branch (symbol) with the larger "metric", taking into account the downstream matched filter.

This means:

•  $a_ν = +1$  was probably sent if the following condition is satisfied:

$$d_{\rm +1}(\nu \cdot T) > d_{\rm -1}(\nu \cdot T) $$

$$\Rightarrow \hspace{0.3cm} d(\nu \cdot T) = d_{\rm +1}(\nu \cdot T) - d_{\rm -1}(\nu \cdot T) > 0\hspace{0.05cm}.$$

The upper block diagram has been drawn according to this description for better understanding.

• Of course, matched filtering could instead also be moved to the right of the discrimination, as shown in the lower model .
• Then only one filter has to be implemented.

In  Exercise 4.13 , this FSK demodulator is discussed in detail. On the exercise page you can also see the corresponding signal waveforms.

Error probability of orthogonal FSK

$\text{Definition:}$  One speaks of   orthogonal FSK,

• if the modulation index   $h$  is an integer multiple of  $0.5$ , and thus
• the frequency deviation  $Δf_{\rm A}$  is an integer multiple of  $0.25/T$.

For the coherent demodulator, the correlation coefficient between  $d_{+1}(T_{\rm D})$  and  $d_{–1}(T_{\rm D})$  is zero at all detection times. Thus, the magnitude  $|d(T_{\rm D})|$ - the distance of the detection samples from the threshold - is constant. No pulse interference occurs.

If one assumes

• orthogonal FSK,
• an AWGN channel  $($captured by the quotient  $E_{\rm B}/N_0)$, and
• the coherent demodulation described here

then the bit error probability is given by:

$$p_{\rm B} = {\rm Q}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/(2 N_0 }) \hspace{0.1cm}\right ).$$

This corresponds to a degradation of  $3 \ \rm dB$ compared to  BSPK  because

• although the coherent FSK demodulator gives the same result with respect to the useful signal,
• and the noise powers in the two branches are also exactly the same as with BPSK,
• due to the subtraction, the total noise power is doubled.

However, while non-coherent demodulation is not possible under any circumstances in binary phase modulation (BPSK), there is also a non-coherent FSK demodulator, but with a somewhat increased probability of error:

$$p_{\rm B} = {1}/{2} \cdot {\rm e}^{- E_{\rm B}/{(2N_0) }}\hspace{0.05cm}.$$

The derivation of this equation is given in the chapter  Carrier Frequency Systems with Non-Coherent Demodulation  of the book "Digital Signal Transmission".

Binary FSK with Continuous Phase Matching

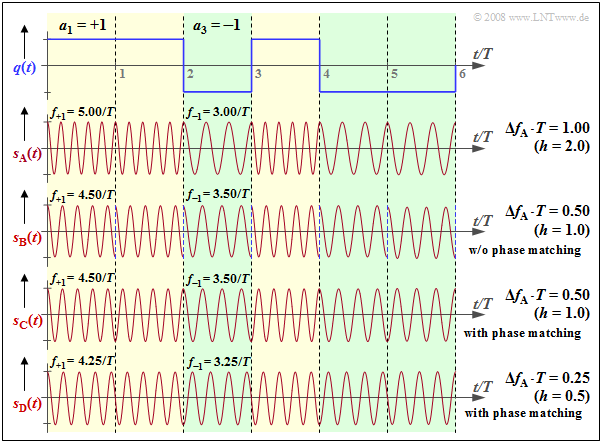
We continue to consider the orthogonal FSK. The graph shows the source signal  $q(t)$  at the top and, drawn below, the FSK signal  $s_{\rm A}(t)$  with frequency deviation  $Δf_{\rm A} = 1/T$ ⇒ modulation index  $h = 2 · Δf_{\rm A} · T = 2$. The following should be noted about the other signal waveforms:

Binary FSK signals with  $h = 2$,  $h = 1$  and  $h = 0.5$, partially with phase matching

• The FSK signal $s_{\rm B}(t)$  uses instantaneous frequencies  $f_{+1} = 4.5/T$,  $f_{–1} = 3.5/T$   ⇒   $Δf_{\rm A} ·T = 0.5$   ⇒   $h = 1.$ This FSK is also orthogonal because of $h = 1$  $($multiple of  $0.5)$.  However, with smaller  $h$ , the bandwidth efficiency is better   ⇒   the spectrum  $S_{\rm B}(f)$  is narrower than  $S_{\rm A}(f)$.

• However, in the signal $s_{\rm B}(t)$ , one can detect a phase jump by  $π$ at each symbol boundary, which again results in a broadening of the spectrum. Such phase jumps can be avoided by phase matching. This is then referred to as Continuous Phase Modulation  $\rm (CPM)$.

• Also, for the CPM signal  $s_{\rm C}(t)$ ,  $f_{+1} = 4.5/T, f_{–1} = 3.5/T$  and  $h = 1$ hold. . In the range  $0$ ... $T$ , the coefficient  $a_1 = +1$  is represented by  $\cos (2π·f_{+1}·t)$ , and in the range  $T$ ... $2T$ , on the other hand, the coefficient  $a_2 = +1$ , which is also positive, is represented by the function  $\ –\cos (2π·f_{+1}·t)$  shifted by  $π$ .

• The modulation index  $h = 0.5$  of signal $s_{\rm D}(t)$  is the smallest value that allows orthogonal FSK ⇒ Minimum Shift Keying  $\rm (MSK)$. In MSK, four different initial phases are possible at each symbol boundary, depending on the previous symbols.

The interactive applet Frequency Shift Keying & Continuous Phase Modulation (CPM) is available to illustrate the facts presented here.

MSK – Minimum Shift Keying

Block diagram for generating a MSK signal

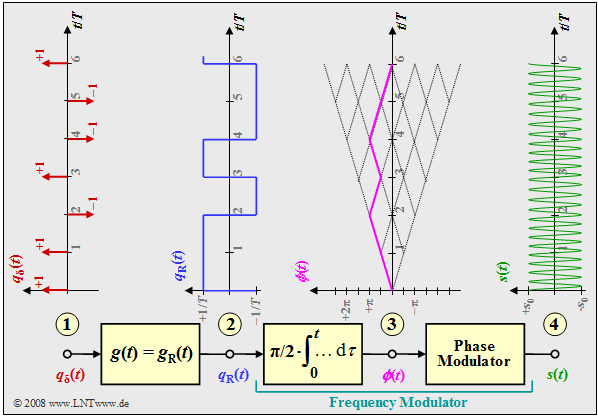
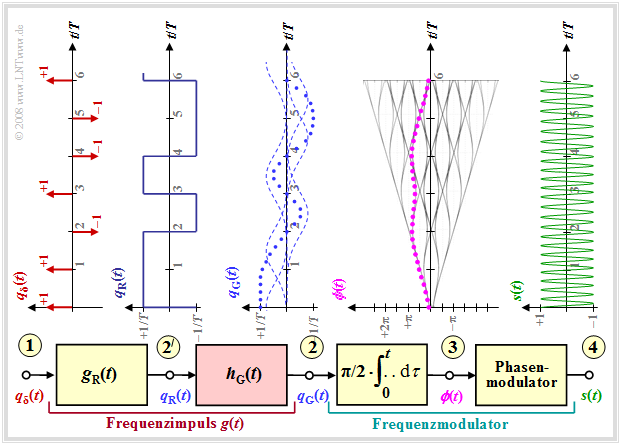
The image shows the block diagram for generating an MSK modulation and typical signal properties at various points of the MSK transmitter. One can recognize

• the digital source signal at point  (1), a sequence of Dirac pulses spaced  $T$ apart, weighted by the coefficients  $a_ν ∈ \{–1, +1\}$:

$$q_\delta(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot \delta (t - \nu \cdot T)\hspace{0.05cm},$$

• the rectangular signal  $q_{\rm R}(t)$  at point  (2)  after convolution with the rectangular pulse $g(t)$  of duration $T$  and height  $1/T$:

$$q_{\rm R}(t) = \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (t - \nu \cdot T)\hspace{0.05cm},$$

• the  frequency modulator  (integrator and downstream phase modulator). For the signal at point (3) :

$$\phi(t) = {\pi}/{2}\cdot \int_{0}^{t} q_{\rm R}(\tau)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$

The phase values at multiples of the symbol duration  $T$  are multiples of  $π/2$, when taking into account the modulation index  $h = 0.5$  for the MSK method. The phase response is linear. From this, the MSK signal at point   (4)  of the block diagram is given by:

$$s(t) = s_0 \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm}t + \phi(t)) = s_0 \cdot \cos (2 \pi \cdot t \cdot (f_{\rm T}+a_{ \nu} \cdot {\rm \Delta}f_{\rm A} )) \hspace{0.05cm}.$$

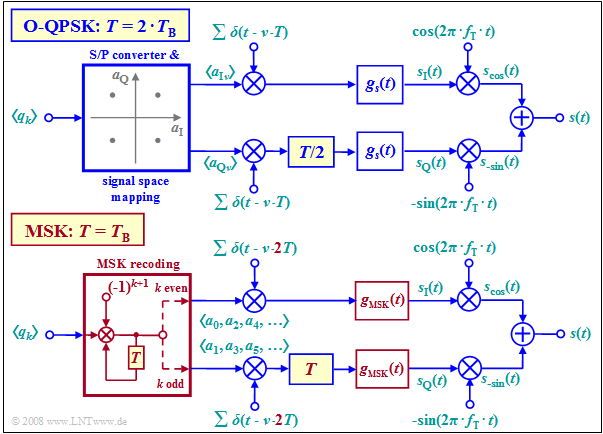
Realizing MSK as Offset–QPSK

Minimum Shift Keying  $\rm (MSK)$ can also be realized by modified implementation of Offset–QPSK  $\rm (O–QPSK)$ .

Compared with the conventional offset QPSK implementation (upper graph), the following modifications must be taken into account, which are highlighted in red in the lower graph:

Conventional O-QPSK and O-QPSK in MSK mode

• The symbol duration  $T$  of MSK is equal to the bit duration  $T_{\rm B}$  of the binary input signal, while in original O-QPSK,  $T = 2 \cdot T_{\rm B}$ .
• Instead of serial-to-parallel conversion and signal space allocation, the source symbols must now be recoded:

$$a_k = (–1)^{k+1} · a_{k–1} · q_k.$$

• All amplitude coefficients  $a_k$  with an even index  $(a_0,\ a_2$, ...$)$  are applied to the Dirac pulse in the upper branch, while 𝑎 $a_1,\ a_3$, ...  are transmitted in the lower branch.
• The spacing of the individual Dirac pulses is now  $2T$  instead of  $T$  and the offset in the quadrature branch is no longer  $T/2$, but  $T$. In both cases, the offset is equal to  $T_{\rm B}$.
• While in conventional O-QPSK implementation any fundamental pulse  $g_s(t)$ is possible, for example a rectangular or root Nyquist pulse, there is only one suitable fundamental pulse for MSK implementation. This spans two symbol durations:

$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} s_0 \cdot \cos \big ({\pi/2 \cdot t}/T \big ) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$

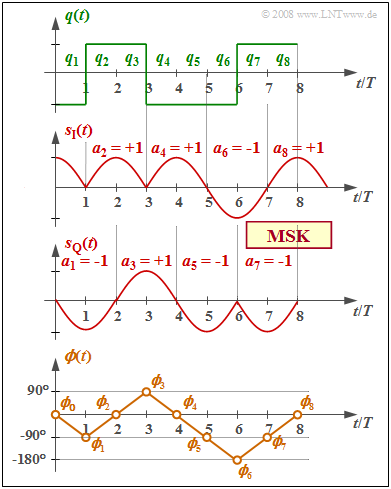
$\text{Example 2:}$ 

Signal waveforms of O–QPSK in MSK mode

• The graph shows the binary bipolar source signal  $q(t)$ at the top,
• in the middle, we see the equivalent TP signals  $s_{\rm I}(t)$  and  $s_{\rm Q}(t)$  in the  $\rm I$ and  $\rm Q$ branches, respectively,
• and below, the phase response  $ϕ(t)$  of the total MSK transmitted signal  $s(t)$.

The recoding  $a_k = (–1)^{k+1} · a_{k–1} · q_k$  is already taken into account, as well as the MSK fundamental pulse:

$$g_{\rm MSK}(t) = \left\{ \begin{array} {l} s_0 \cdot \cos ({\pi \cdot t}/{2 \cdot T}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r} } \\{\rm{f\ddot{u}r} } \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$

From the comparison of the top and bottom diagrams, one can see:

• The MSK phase response  $ϕ(t)$  is step-wise linear and increases or decreases by  $90^\circ \ (π/2)$ within each symbol duration, depending on whether  $q_k = +1$  or  $q_k = -1$  currently holds.
• The transmitted signal  $s(t)$  contains the two frequencies  $f_{\rm T} ± 1/(4T)$ in sections. It has basically the same shape as the signal  $s_{\rm D}(t)$  in the section Binary FSK with Continuous Phase Matching.

You can represent this form of MSK realization with the interactive applet: Quaternary Phase Shift Keying und Offset-QPSK  using the following settings::

• Offset–QPSK,
• MSK allocation,
• cosine impulse.

General Description of Continuous Phase Modulation

We will further assume that the source is characterized by the amplitude coefficients  $a_ν$ .  These can be binary as well as  $M$–levelled. However, they should always be considered bipolar, for example   $a_ν\in \{+1, -1\}$.

• The  phase function  $ϕ(t)$  in  Continuous Phase Modulation  $\rm (CPM)$  can be generally represented in the following form (  $(h$  denotes the modulation index$)$:

$$\phi(t) = {\pi}\cdot h \cdot\int_{-\infty}^{t} \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g (\tau - \nu \cdot T)\hspace{0.1cm} {\rm d}\tau \hspace{0.05cm}.$$

• In this representation,  $g(t)$  denotes the  frequency pulse, which must satisfy the following condition:

$$\int_{-\infty}^{+\infty} g (t)\hspace{0.1cm} {\rm d}t = 1 \hspace{0.05cm}.$$

• But the following relationship also holds with the   phase pulse   $g_ϕ(t)$ :

$$\phi(t) = {\pi}\cdot h \cdot \sum_{\nu = - \infty}^{+\infty}a_{ \nu} \cdot g_\phi (t - \nu \cdot T),\hspace{0.2cm}{\rm wobei}\hspace{0.2cm}g_\phi(t) = \int_{-\infty}^{t} g (\tau )\hspace{0.1cm} {\rm d}\tau\hspace{0.05cm}.$$

Frequency pulse and phase pulse of some CPM variants

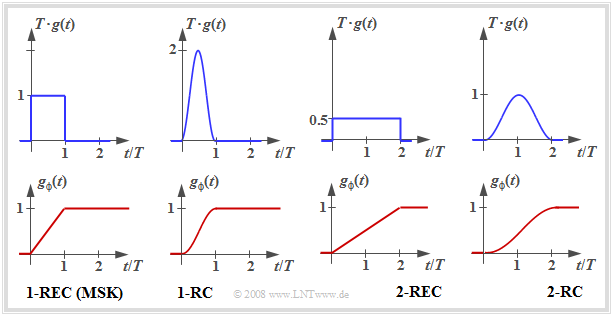
Many CPM variants can be realized by appropriately choosing the pulses  $g(t)$  and  $g_ϕ(t)$ . Some of them are shown below.

• In each case, the graph shows the CPM frequency pulse $g(t)$  at the top and the CPM phase pulse  $g_ϕ(t)$ at the bottom.
• The two graphs on the left describe  $\rm MSK$.
• The   $\rm 1–REC$  designation indicates that  $g(t)$  spans a single symbol duration  $(T)$  and is rectangular in shape.

The other CPM variants were designed with the goal of further reducing the already small bandwidth of the MSK signal:

• For  $\rm 1–RC$ , a narrower power-spectral density results just because of the "softer" raised-cosine pulse  $g(t)$  compared to the rectangular pulse.
•   $\rm 2–RC$  and  $\rm 2–REC$ are "Partial–Response" impulses, each over  $2T$.  This softens the phase response. However, it also makes demodulation more difficult, since selective pseudo-steps are introduced into the data signal.

The calculation of CPM procedures in the spectral range is complicated in general. Only the special case "MSK" leads to equations which are easy to handle, as shown in  Exercise A4.14 .

$\text{Conclusion:}$  Continuous Phase Modulation  $\rm (CPM)$  is not a phase modulation, but is a nonlinear digital frequency modulation $\rm (FSK)$, with the goal of

• guaranteeing a constant magnitude envelope (dips in the envelope lead to problems even with small nonlinearities),
• to enable a continuous phase progression (phase jumps broaden the spectrum).

For more detailed information we refer to the technical literature, for example in the recommended book   [Kam04].

GMSK – Gaussian Minimum Shift Keying

One advantage of MSK is the low bandwidth requirement, because: Bandwidth is always expensive.

• A slight modification to   Gaussian Minimum Shift Keying  $\rm (GMSK)$  further narrows the spectrum.
• This type of modulation is used, for example, in the GSM  mobile communications standard.

Signal waveforms in Gaussian Minimum Shift Keying  $\rm (GMSK)$ KORREKTUR

From the graph one can see:

• the frequency pulse  $g(t)= g_{\rm G}(t)$  is now no longer rectangular like  $g_{\rm R}(t)$, but has flatter edges.

• This results in a smoother phase response at point   (3)  than in  MSK, where  $ϕ(t)$  rises / falls linearly with each symbol.

• One achieves the smoother GMSK phase transitions by using a Gaussian low-pass.  With the system theoretic cutoff frequency $f_{\rm G}$, its frequency response and impulse response are as follows:

$$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 \cdot f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 \cdot f_{\rm G}\cdot t)^2}\hspace{0.05cm}.$$

• The resulting frequency pulse  $g(t)$  at point  (2)  is obtained by convolution of $g_{\rm R}(t)$  and  $h_{\rm G}(t)$.

• The signal  $s(t)$  at point  (4)  in GMSK now no longer has a constant section by section frequency (per symbol duration) as it does in MSK, even though this is difficult to see with the naked eye from the above graph.

$\text{Example 3:}$  In the GSM method, the 3dB cutoff frequency is specified as  $f_{\rm 3dB} = 0.3/T$ , where the following relationship exists between the system theoretic frequency and the 3dB cutoff frequency:

$$H_{\rm G}(f= f_{\rm 3 \hspace{0.03cm}dB}) = {\rm e}^{-\pi\cdot ({f_{\rm 3 \hspace{0.03cm}{dB} } }/{2 f_{\rm G} })^2} = {1}/{\sqrt{2} }$$

$$\Rightarrow\hspace{0.15cm} f_{\rm 3 dB} = f_{\rm G} \cdot \sqrt { {4}/{\pi}\cdot {\rm ln }\sqrt{2} }\approx {2}/{3}\cdot f_{\rm G} \hspace{0.05cm}.$$

From  $f_{\rm 3dB} = 0.3/T$ ,  $f_{\rm G} · T ≈ 0.45$ also follows.

Exercises for the chapter

Exercise 4.13: FSK Demodulation

Exercise 4.14: Phase Progression of the MSK

Exercise 4.14Z: Offset QPSK vs. MSK

Exercise 4.15: MSK Compared with BPSK and QPSK

Exercise 4.15Z: MSK Basic Pulse and MSK Spectrum

Exercise 4.16: Comparison between Binary PSK and Binary FSK